Теория вероятностей и математическая статистика. Обзорная лекция

1.

Теория вероятностей и
математическая статистика
Обзорная лекция

2.

Случайные события

3.

• Основными понятиями теории вероятностей являются: опыт;
событие; вероятность.
• Опыт (испытание) – действие, выполняющееся при
осуществлении комплекса условий.
• Событие – всякое явление, которое может произойти или не
произойти в результате опыта.
• События подразделяются на: достоверные; невозможные;
случайные. События обозначаются заглавными латинскими
буквами с начала алфавита (А, В, С,…).
• События называются совместными, если появление одного из
них не исключает появление других событий, и несовместными,
если появление одного из них исключает появление остальных
событий в одном и том же опыте.

4.

• Пример 1. В течение одной экзаменационной сессии студент
сдает экзамены по физике и математике. Через событие А
обозначим получение 9 баллов по математике, событие В получение 8 баллов по математике на той же сессии, событие С получение 8 баллов по физике. Выбрать из этих трех событий
совместные и несовместные события.
• Равновозможными называются события, ни одно из которых не
является более возможным, чем остальные.
• Группа несовместных событий называется полной группой, если
в результате опыта обязательно наступит одно из событий,
входящих в эту группу.
• Противоположными называются два несовместных события,
образующих полную группу.
• Событие, противоположное событию А, обозначается А .

5.

Действия над событиями
• Под суммой нескольких событий будем понимать появление хотя
бы одного из этих событий.
• Произведение
нескольких
событий
–
это
событие,
заключающееся в появлении всех этих событий.
• Подчеркнутые слова являются ключевыми в этих определениях.
• Так событие А+В в случае несовместных событий означает или
появление события А, или события В. Если же события
совместные, то под суммой А+В понимают появление только
события А, или только события В или обоих событий вместе.
• Пример 2. Два стрелка стреляют по разу в одну мишень.
Событие А1 – попал первый стрелок, А2 – второй. Через события
А1 и А2 выразить события: 1) В – попал хотя бы один стрелок, 2) С
– не попали оба.

6.

• Пример 2. Два стрелка стреляют по разу в одну мишень.
• Событие А1 – попал первый стрелок, А2 – второй.
• Через события А1 и А2 выразить события:
• 1) В – попал хотя бы один стрелок, 2) С – не попали оба.
Ответ:
_
_
• 1) B A1 A2 или B A1 A2 A2 A1 A1 . A2
_
_
• 2) B A1 A2

7.

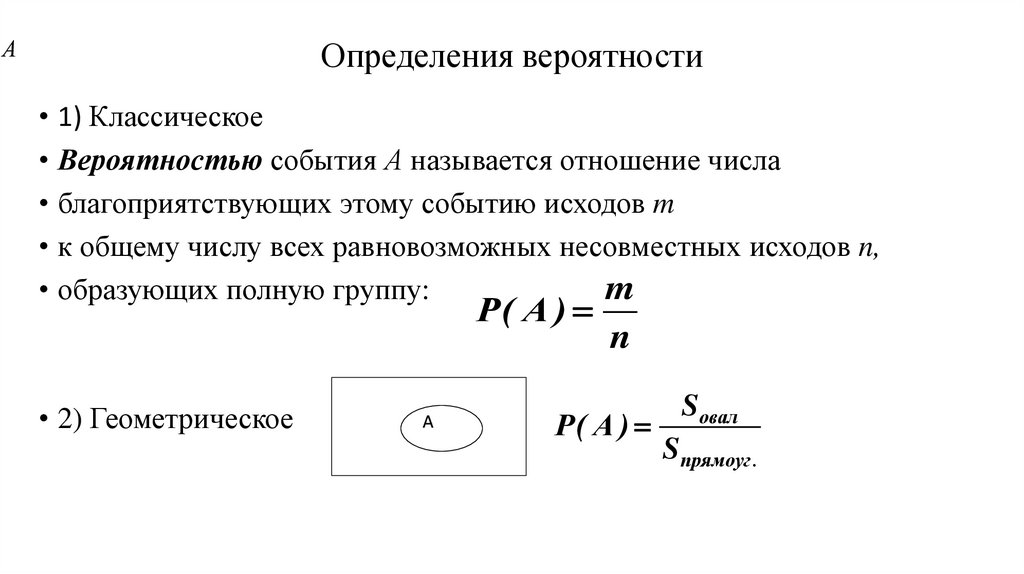
А
Определения вероятности
• 1) Классическое
• Вероятностью события А называется отношение числа
• благоприятствующих этому событию исходов m
• к общему числу всех равновозможных несовместных исходов n,
• образующих полную группу:
m
Р( A )
• 2) Геометрическое
А
n
Р( A )
Sовал
Sпрямоуг .

8.

3) Статистическое
Относительной частотой события А в данной серии опытов
называется отношение числа опытов m, в которых событие А
наступило, к общему числу проведенных опытов n:
m
W A
n
Статистической вероятностью называется постоянное
число, около которого группируются относительные частоты
этого события по мере увеличения числа испытаний.
m
Р(А).
W A
n
n

9.

Основные теоремы
1. Теорема сложения вероятностей совместных событий
Р А В Р А Р В Р А В
2. Теорема сложения вероятностей несовместных событий
Р А В Р А Р В
Следствие
Р А 1 Р А .
3. Теорема умножения вероятностей зависимых событий
Р A В P ( A) P ( B A) P ( B ) P ( A B )
4. Теорема умножения вероятностей независимых событий
Р А В Р А Р В

10.

Пример 3. Стрелок производит три выстрела, вероятность
попадания при каждом известна и равна р. Найти вероятность
того, что мишень будет поражена: 1) один раз; 2) два раза.
Обозначим события:
событие Аi – попадание при i – ом выстреле ( i 1,3 ) ,
событие В – мишень поражена один раз при трех
выстрелах, В2 – два раза
B A1 A2 A3 A1 A2 A3 A1 A2 A3
2
P( B ) pqq qpq qqp 3 pq .
P( B2 ) ppq qpp pqp 3 p 2 q.

11.

,
,
.
Повторение испытаний в одинаковых условиях
1. Формула Бернулли (p=const, q=1-p).
Pn(m) - вероятность того, что событие наступит m раз в n опытах (n
невелико)
Pn ( m ) C p q
m
n
m
n m
n!
C
m!(n m)!
m
n
2. Локальная теорема Лапласа (Муавра-Лапласа)
1
k np
(
x
)
e
x
2
npq
3. Формула Пуассона (n велико, р мало λ=np<10)
1
1
Pn (k )
e
npq 2
x2
2
1
( x)
npq
4. Интегральная теорема Лапласа
Рn k1 k k2 Ф( x2 ) Ф( x1 )
x1
k1 np
npq
k 2 np
x2
npq
x2
2
m
Pn (m ) e
m!
Ф( х)
x
1
e
2 0
z2
2 dz

12.

Пример 4. Вероятность потери одного вызова на АТС равна 0,1. Найти
вероятность того, что из пяти вызовов: 1) три закончатся разговором 2) не
менее четырех закончатся разговором.
p=0,1 , q=0,9
P8 ( 1 ) C53 p 3q 2 10 0,001 0,92.
Где допущена ошибка?

13.

Пример 4. Вероятность потери одного вызова на АТС равна
0,1. Найти вероятность того, что из пяти вызовов: 1) три
закончатся разговором 2) не менее четырех закончатся
разговором.
p= 0,9 ; q= 0,1.
5!
3
2
( 0,9 ) ( 0,1 ) 0,0729
3! 2!
1.
3
3
3
P5( 3 ) C5 p q
2.
P5 ( m 4 ) P5 ( 4 ) P5 ( 5 ) C54 p 4 q1 C55 p 5 0,919

14.

Случайные величины
Случайной называют величину, принимающую в результате
опыта единственное значение, заранее неизвестное и зависящее от
случайных причин.
Случайные величины обычно обозначаются заглавными
латинскими буквами с конца алфавита X, Y, Z, а их значения –
строчными буквами x, y, z.
Дискретной называется такая случайная величина, которая
принимает значения, изолированные друг от друга.
Случайная величина называется непрерывной, если она
может принимать все значения из некоторого конечного или
бесконечного промежутка.
Законом распределения случайной величины называют
соотношение между возможными значениями случайной величины
и их вероятностями

15.

P
xX
p1n212n
Закон распределения дискретной случайной величины
• Пусть X – дискретная случайная величина, которая может
принимать значения х1, х2,…, хn с вероятностями р1, р2,…, рn,
соответственно. Если n невелико, эту информацию удобно
представить в виде ряда распределения
X
x1
x2
…
xn
P
p1
p2
…
pn
x1 x2 x3 ... xn
n
n
i 1
i 1
p( X xi ) pi 1
• Это равенство называется условием нормировки для дискретной
случайной величины.

16.

Пример 5. Вероятность попадания в мишень для первого стрелка
равна 0,9, для второго – 0,8. Составить закон распределения для
случайной величины Х – числа попаданий в мишень, если каждый
стрелок стреляет по одному разу.
Аi –в мишень попал i-й стрелок (i=1,2), Bк – число попаданий в
мишень, к = 0,2.
B0 A1 A2
P( X 0 ) P( B0 ) P( A1 ) P( A2 ) 0,1 0,2 0,02
P( X 1 ) P( B1 ) P( A1 A2 A1 A2 ) 0,9 0,2 0,1 0,8 0,26
P( X 2 ) P( B2 ) P( A1 A2 ) P( A1 )P( A2 ) 0,9 0,8 0,72
X
0
1
2
P
0,02
0,26
0,72

17.

:
Функцией распределения случайной величины называется функция
F(x), которая для любого действительного числа х равна вероятности того,
что случайная величина примет значение, меньшее значения аргумента
функции x:
F( x ) P( X x )
0 F( x ) 1
P( a X b ) F( b ) F( a )
Основные числовые зарактеристики
1. Для дискретной случайной величины математическое
ожидание определяется как сумма произведений всех ее
возможных значений на их вероятности:
n
M ( x ) xi pi .
i 1
М(х)- характеризует
случайной величины.
среднее
арифметическое
значение

18.

2. Дисперсией случайной величины называется математическое
ожидание квадрата отклонения данной случайной величины от ее
математического ожидания:
2
D( X ) M( X 2 ) M 2 ( X )
(1)
(2)
D( X ) M X M( X )
3. Средним квадратическим отклонением случайной величины
называется квадратный корень из ее дисперсии:
( X ) D( X )
D(x) и (x) описывают рассеяние (разброс) случайной величины
относительно среднего.

19.

Непрерывные случайные величины
Плотностью распределения вероятностей непрерывной
случайной величины называют первую производную функции
распределения случайной величины:
f ( x ) F'( x )
1. Вероятность попадания случайной величины Х в интервал (a, b)
b
равна:
P( a X b ) f ( x )dx
a
2. Условие нормировки:
x
3.
F( x ) f ( x )dx
f ( x )dx 1

20.

Числовые характеристики непрерывных случайных
величин
1. Математическое ожидание:
2. Дисперсия
M ( X ) xf ( x )dx.
2
2
2
D( X ) M ( X ) ( M ( X )) x f ( x )dx xf ( x )dx
3. Среднее квадратическое отклонение
( X ) D( X )
2

21.

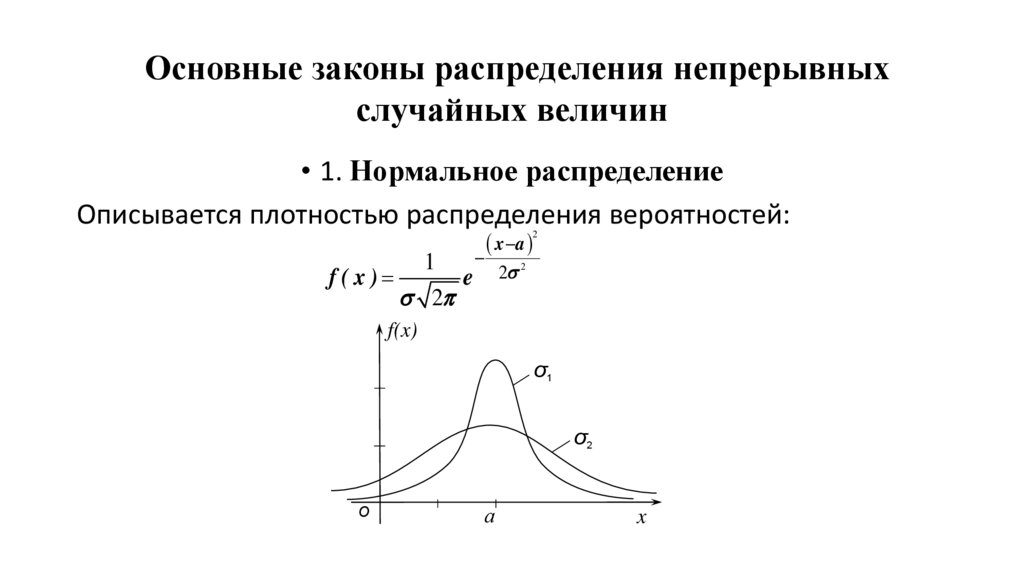
Основные законы распределения непрерывных
случайных величин
• 1. Нормальное распределение
Описывается плотностью распределения вероятностей:
f( x)
1
2
x a
2
e 2
2
f(x)
σ1
σ2
O
а
x

22.

Параметры а=M(x), a ( X ) D( X ) .
Вероятность попадания в заданный интервал нормально
распределенной случайной величины:
a a
P( X )
где Ф(х) – функция Лапласа
z2
x
e 2 dz
1
Ф( х)
2 0
Вероятность заданного отклонения от среднего
Правило трех сигм
Р ( a 3 ,a 3 ) 1
P( X a ) 2Ф

23.

2. Показательное распределение
Описывается плотностью распределения вероятностей:
0 ,t 0 ,
f ( t ) t
,t 0.
e
λ>0
f(t)
O
P( T ) e
e
M(T )
1
t
D( T )
1
2
(T )
1

24.

3. Равномерное распределение
Описывается плотностью распределения вероятностей:
0 , x a,
f ( x ) c, a x b,
0 , x b,
c
1
b a
f(x)
с