Похожие презентации:
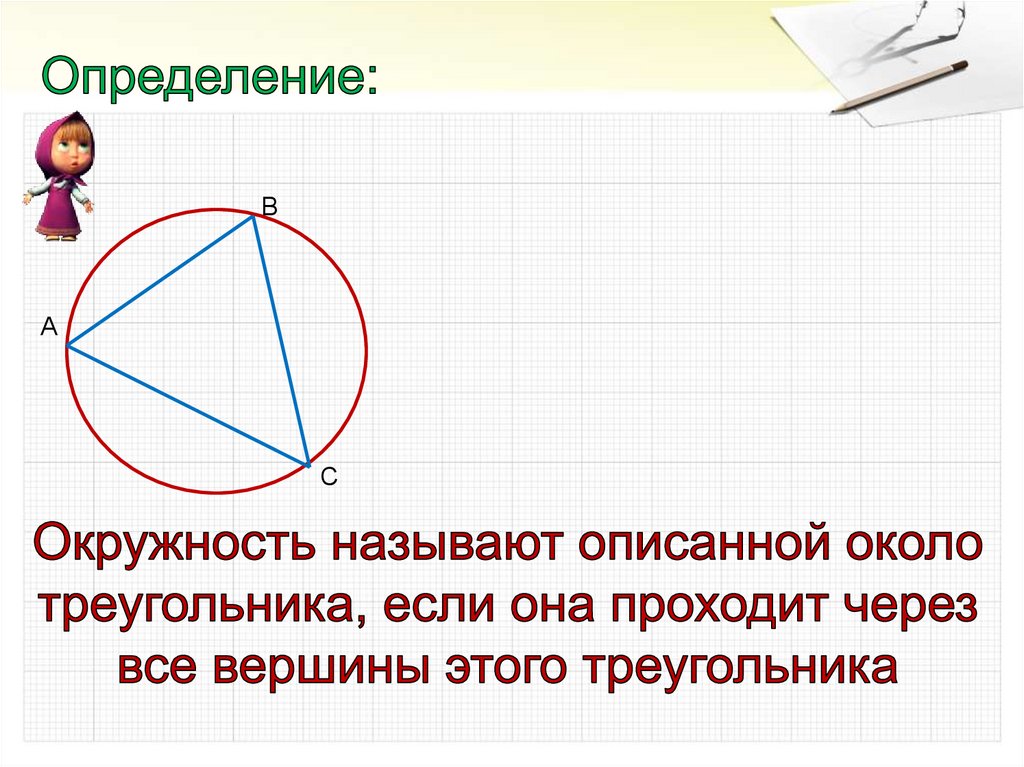
Описанная и вписанная окружности треугольника
1.
2.
ВА
С
3.
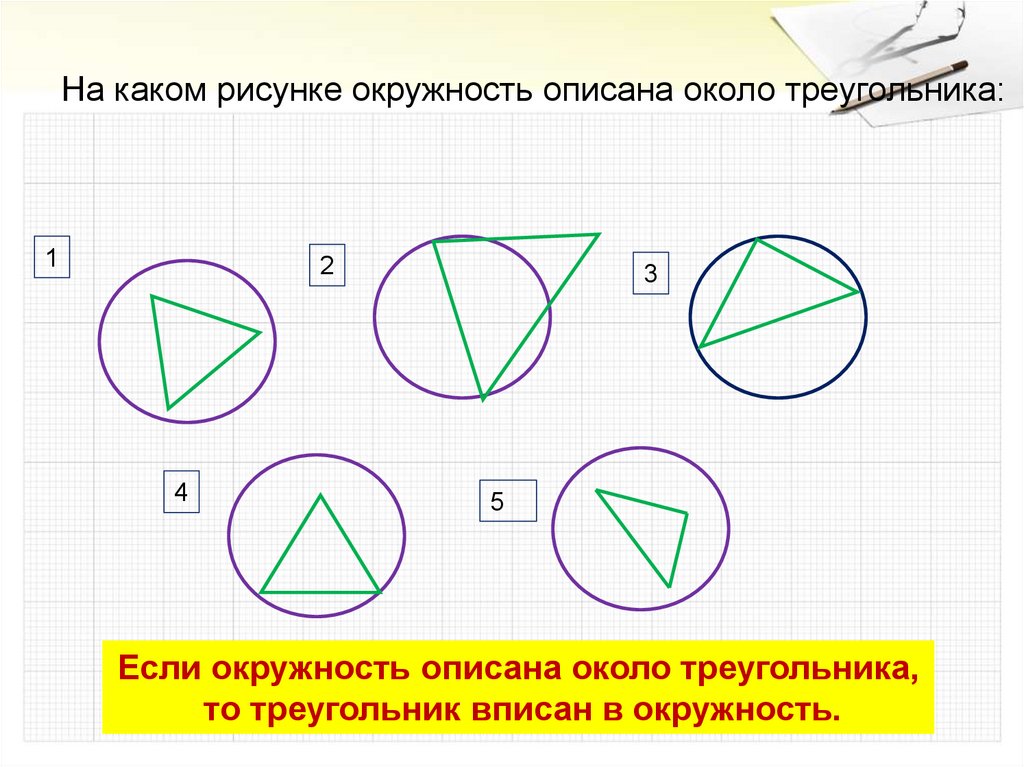
На каком рисунке окружность описана около треугольника:1
2
4
3
5
Если окружность описана около треугольника,
то треугольник вписан в окружность.
4.
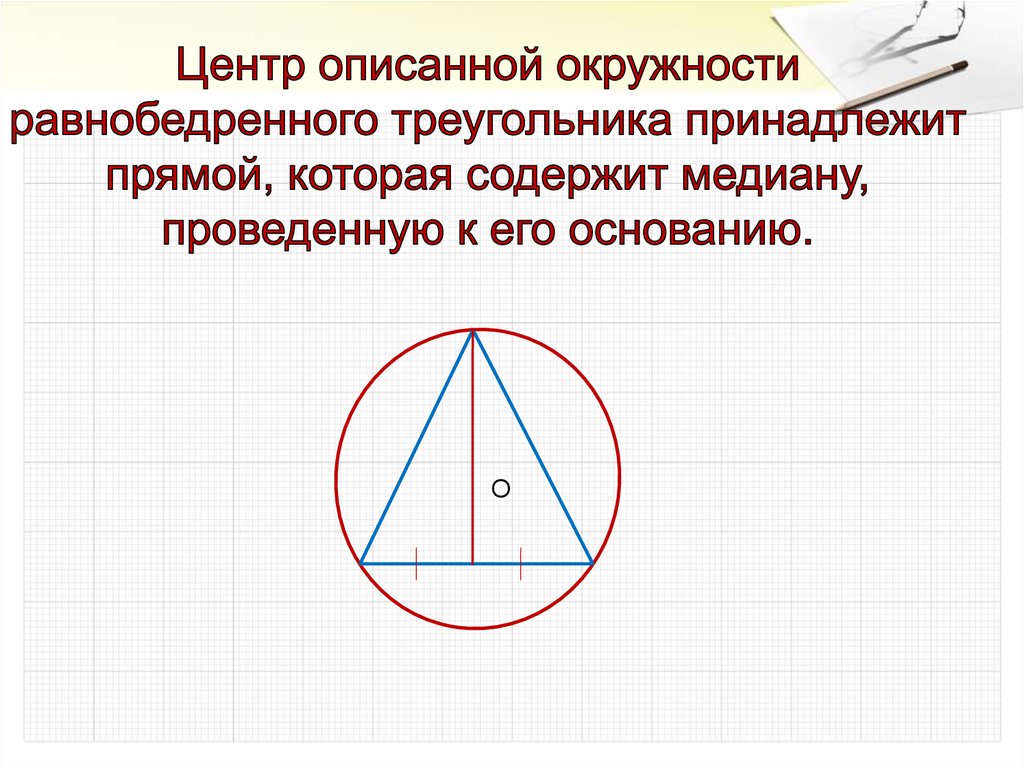
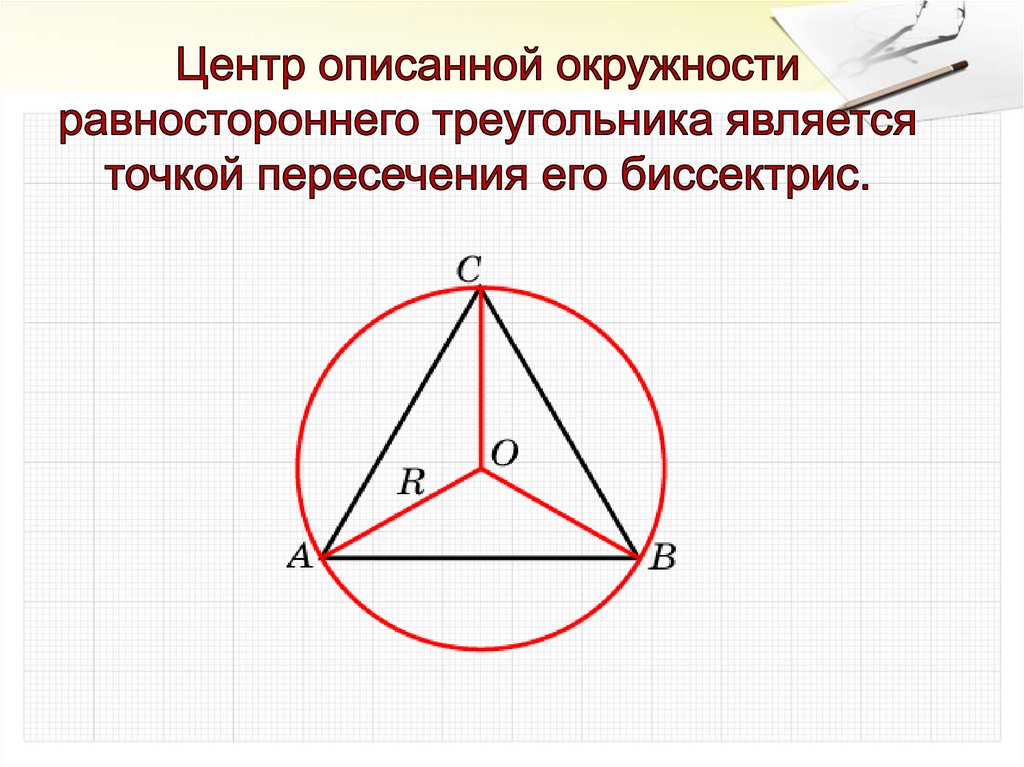
Заметим, около треугольника можно описать только однуокружность
В
p
О
А
k
n
С
5.
6.
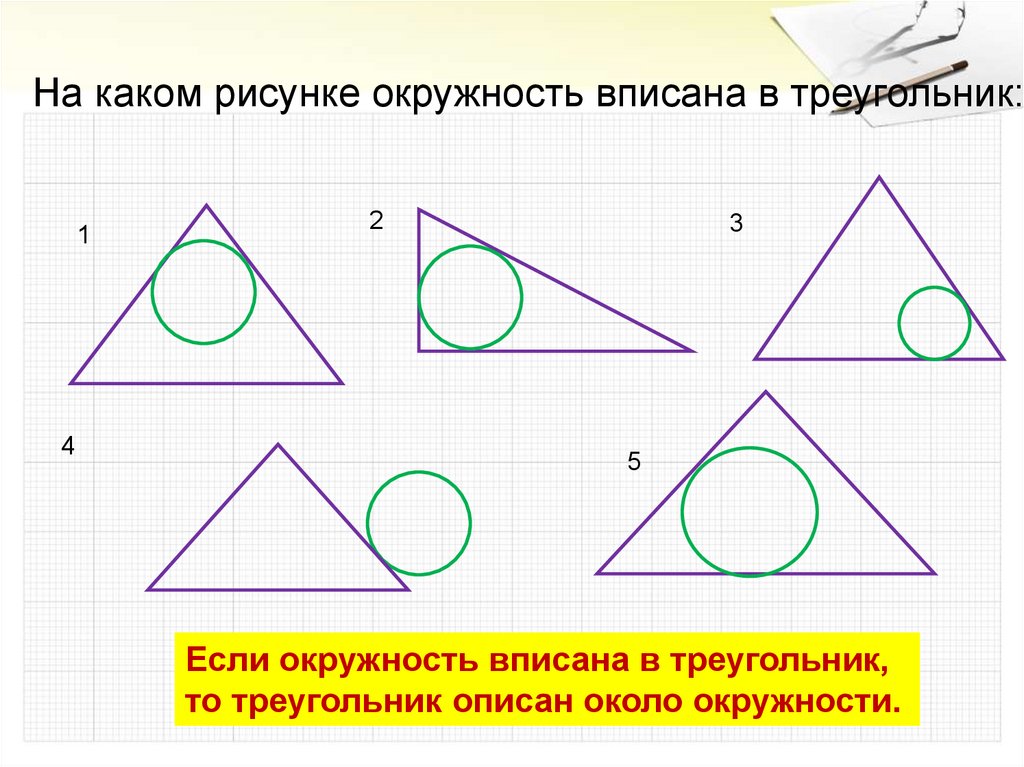
На каком рисунке окружность вписана в треугольник:1
4
2
3
5
Если окружность вписана в треугольник,
то треугольник описан около окружности.
7.
ВС1
А
А1
О
В1
С
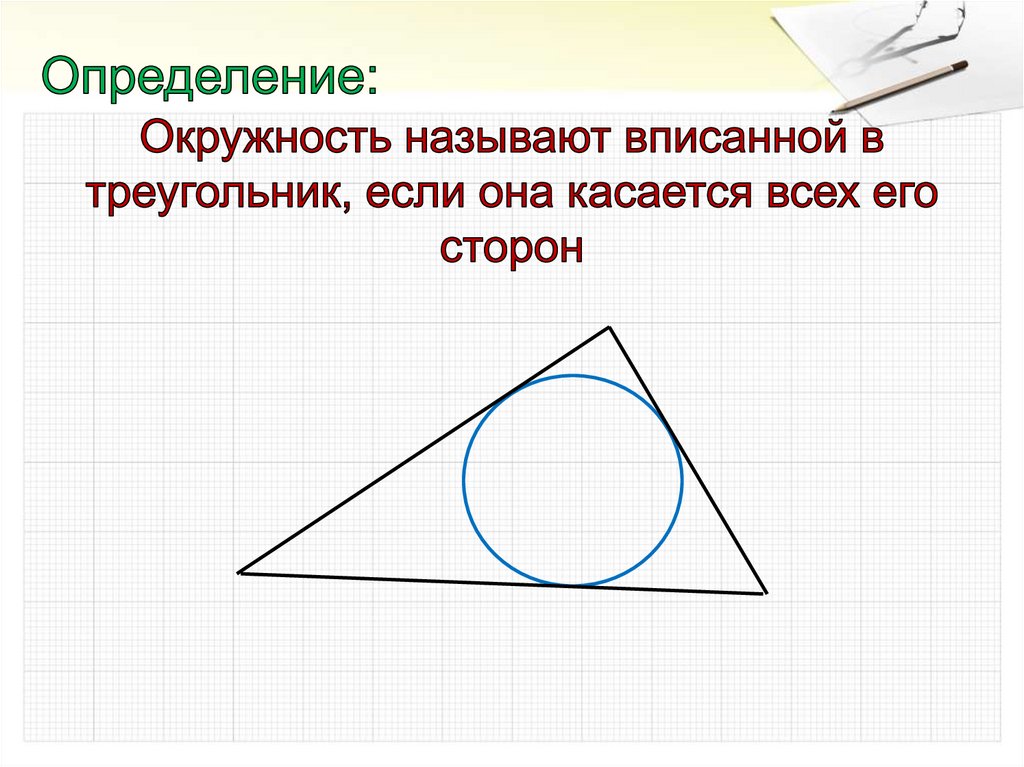
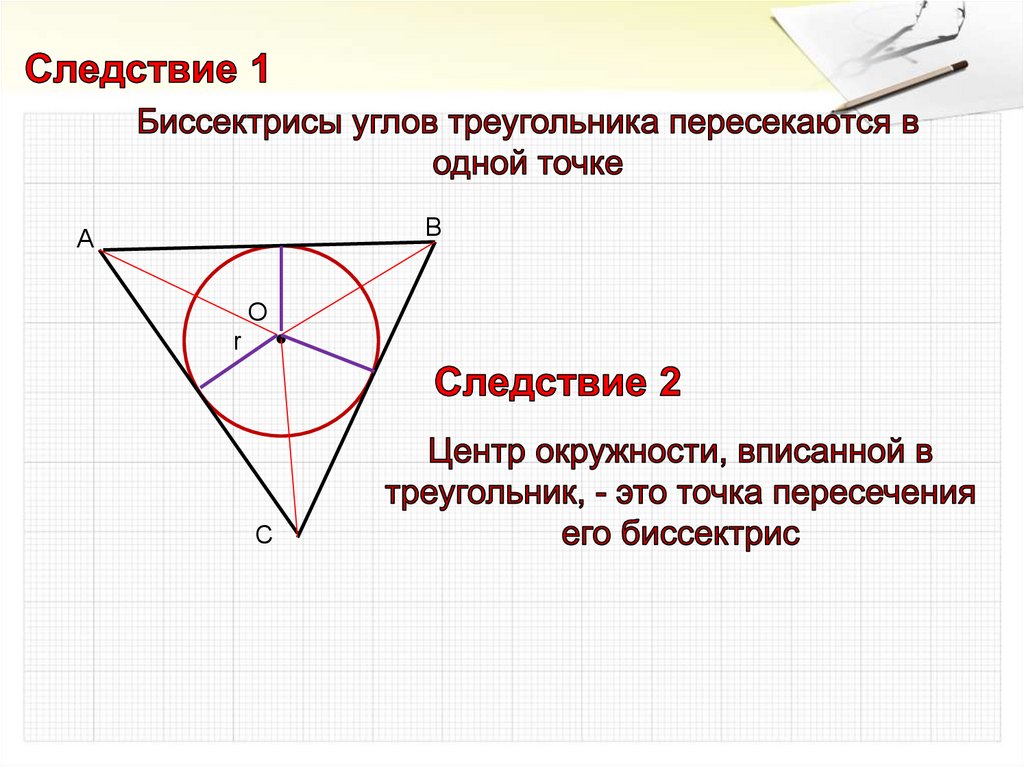
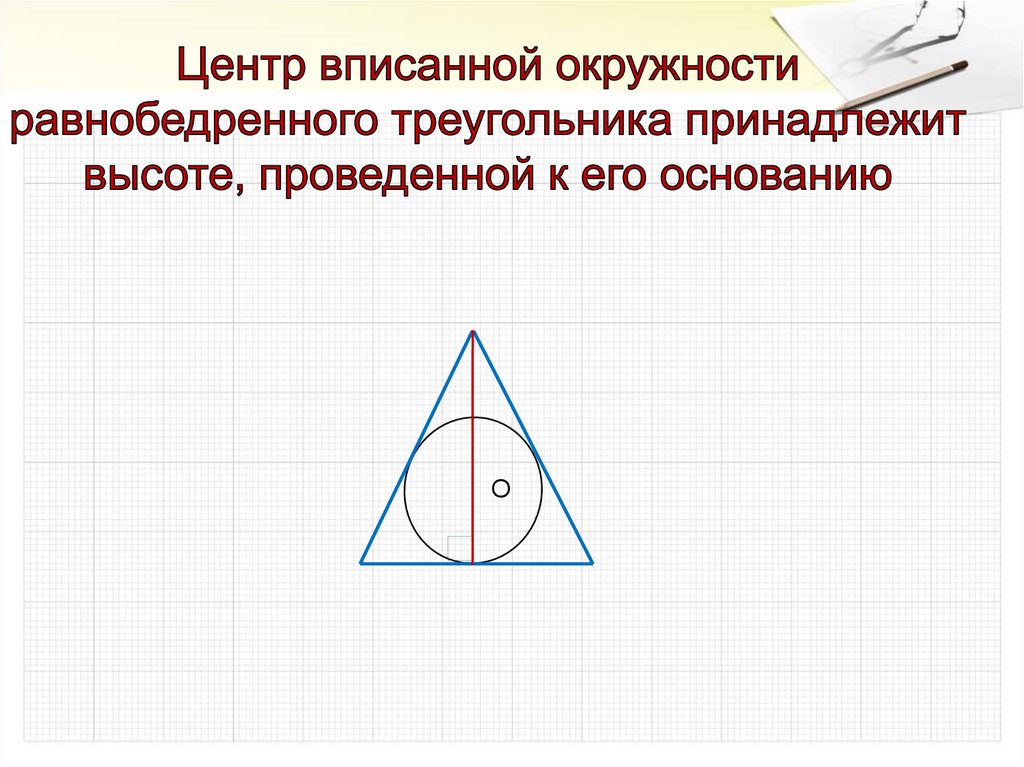
Заметим, в треугольник можно вписать окружность,
и притом только одну.
8.
ВА
О
r
С
9.
a b cr
2
10.
О11.
О12.
13.
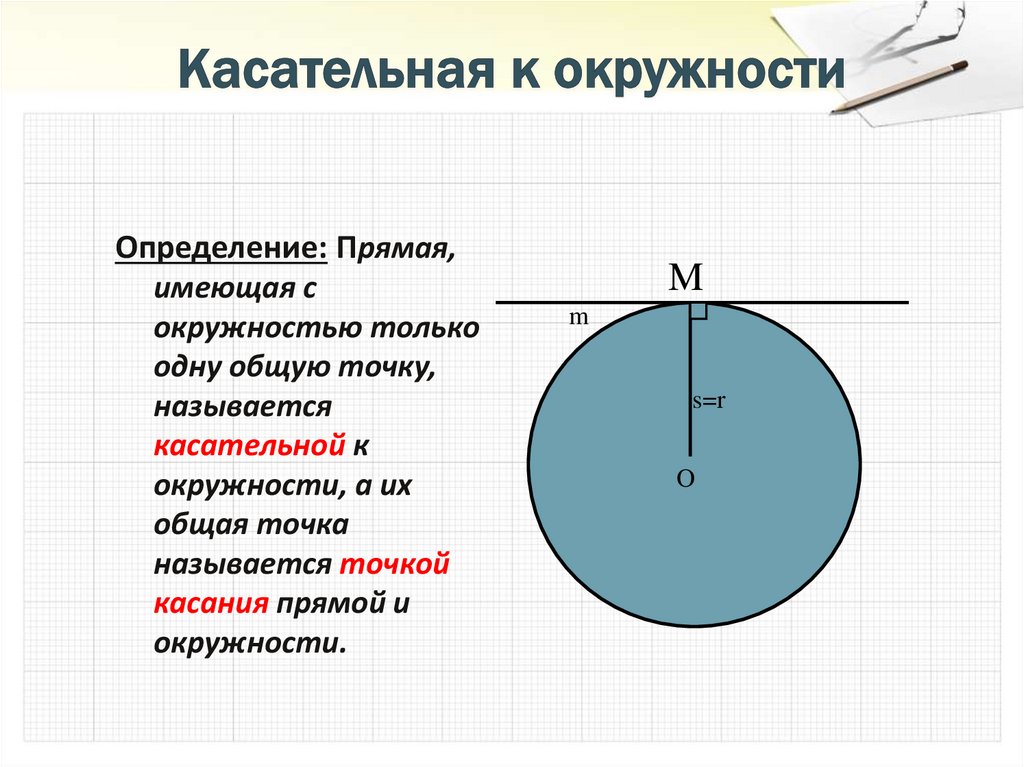
14. Касательная к окружности
Определение: Прямая,имеющая с
окружностью только
одну общую точку,
называется
касательной к
окружности, а их
общая точка
называется точкой
касания прямой и
окружности.
M
m
s=r
O
15. Свойство касательной: Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
m – касательная кокружности с
центром О
М – точка касания
OM - радиус
m OM
M
m
O
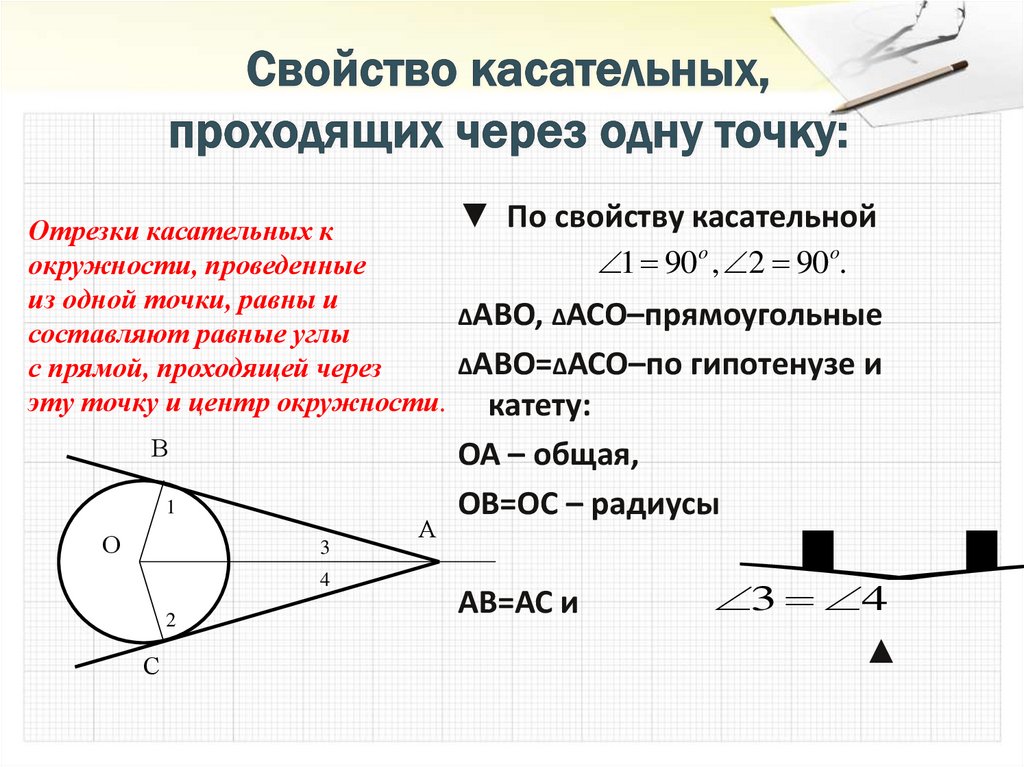
16. Свойство касательных, проходящих через одну точку:
▼ По свойству касательнойОтрезки касательных к
1 90o , 2 90o.
окружности, проведенные
из одной точки, равны и
∆АВО, ∆АСО–прямоугольные
составляют равные углы
∆АВО=∆АСО–по гипотенузе и
с прямой, проходящей через
эту точку и центр окружности. катету:
В
1
О
3
4
2
С
А
ОА – общая,
ОВ=ОС – радиусы
АВ=АС и
3 4
▲
17. Признак касательной: Если прямая проходит через конец радиуса, лежащий на окружности, и перпендикулярна радиусу, то она
Mокружность с центром О
радиуса OM
m – прямая, которая проходит
через точку М
и
m OM
m – касательная
m
O
18.
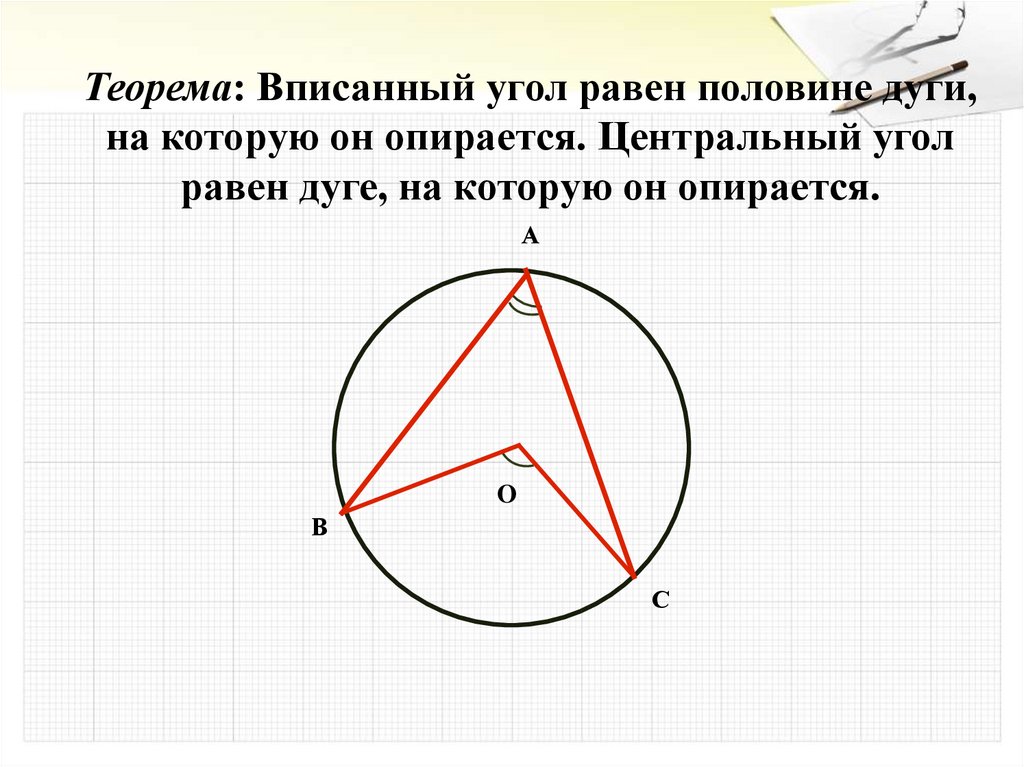
Теорема: Вписанный угол равен половине дуги,на которую он опирается. Центральный угол
равен дуге, на которую он опирается.
А
O
В
С
19.
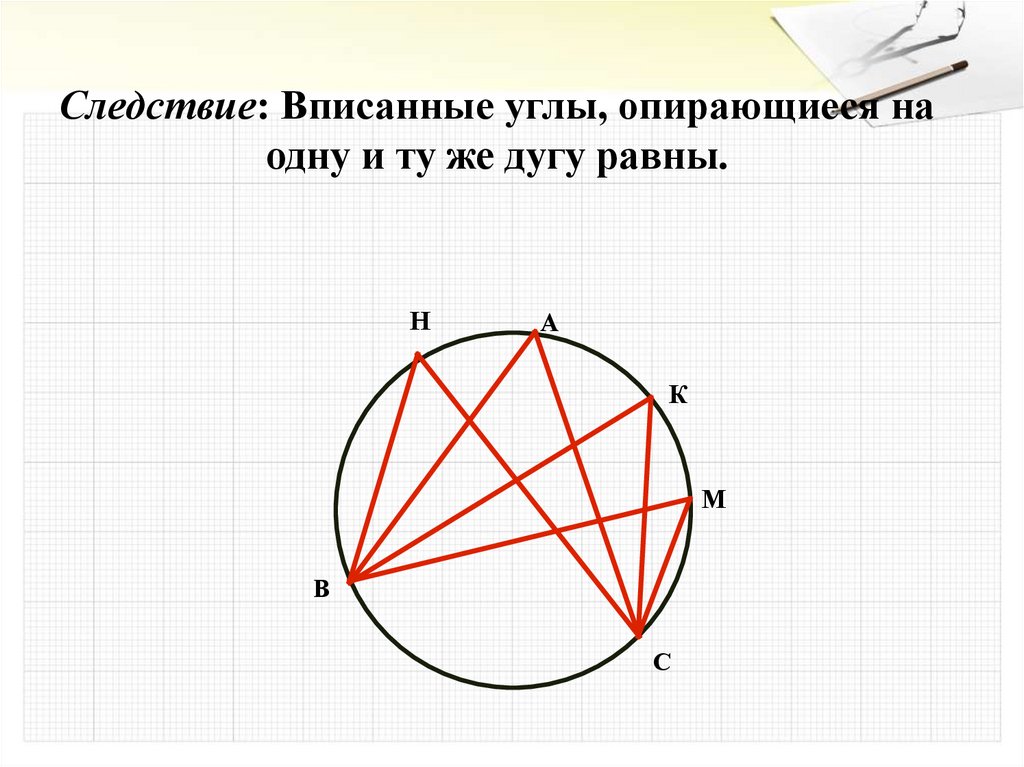
Следствие: Вписанные углы, опирающиеся наодну и ту же дугу равны.
Н
А
К
М
В
С
20.
Следствие: Вписанный угол, опирающийся надиаметр - прямой.
С
А
.
О
В
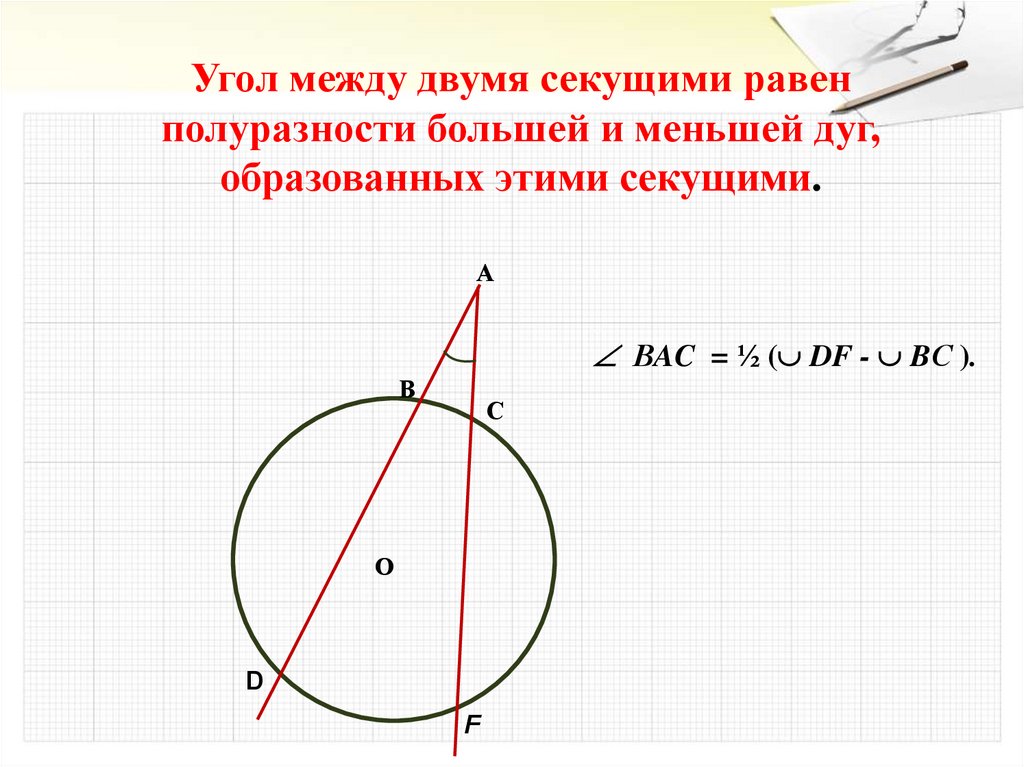
21.
Угол между двумя секущими равенполуразности большей и меньшей дуг,
образованных этими секущими.
А
ВAC = ½ ( DF - BС ).
В
С
О
D
F
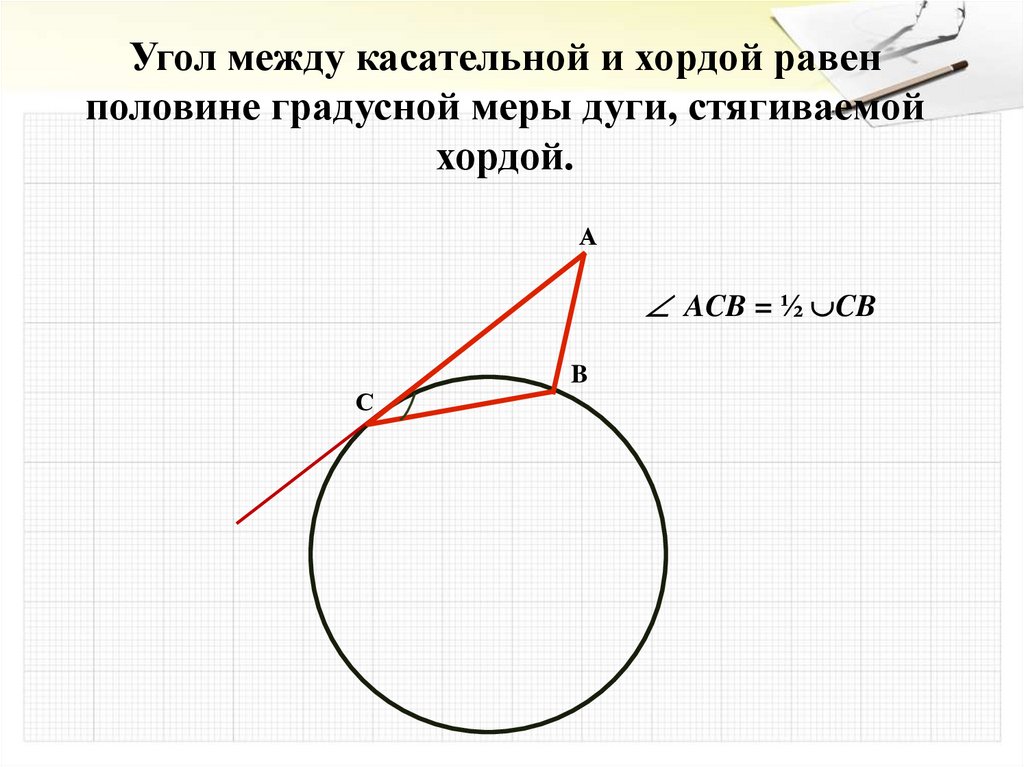
22.
Угол между касательной и хордой равенполовине градусной меры дуги, стягиваемой
хордой.
А
ACB = ½ CB
С
B
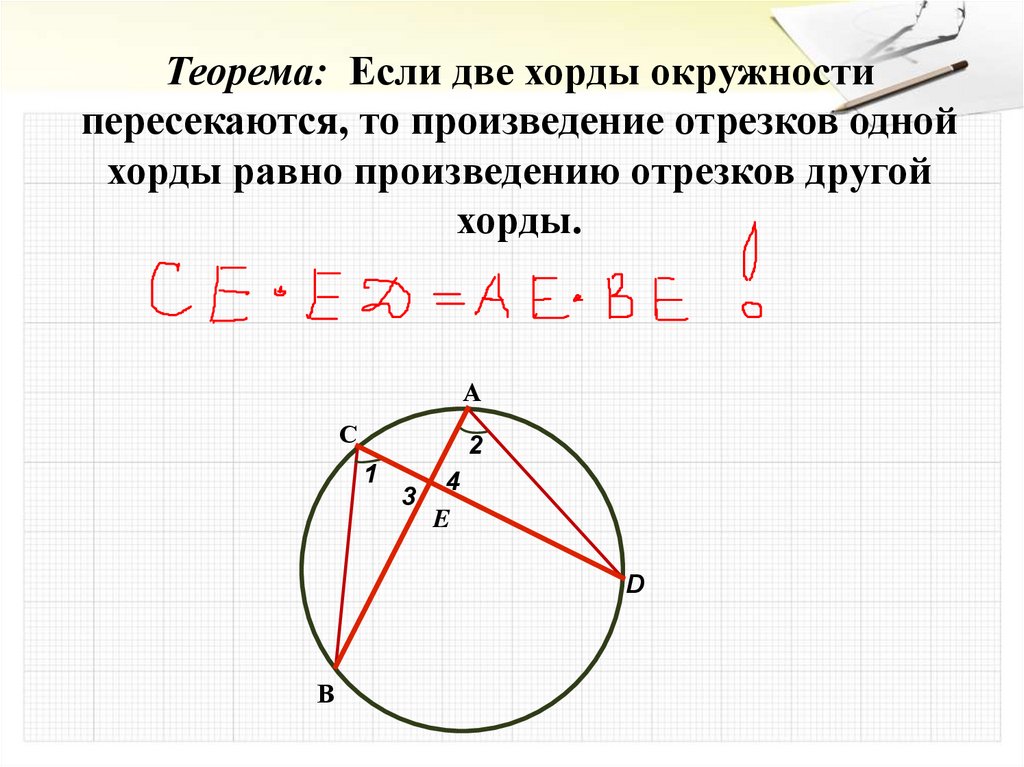
23.
Теорема: Если две хорды окружностипересекаются, то произведение отрезков одной
хорды равно произведению отрезков другой
хорды.
А
С
2
1
3
4
E
D
В
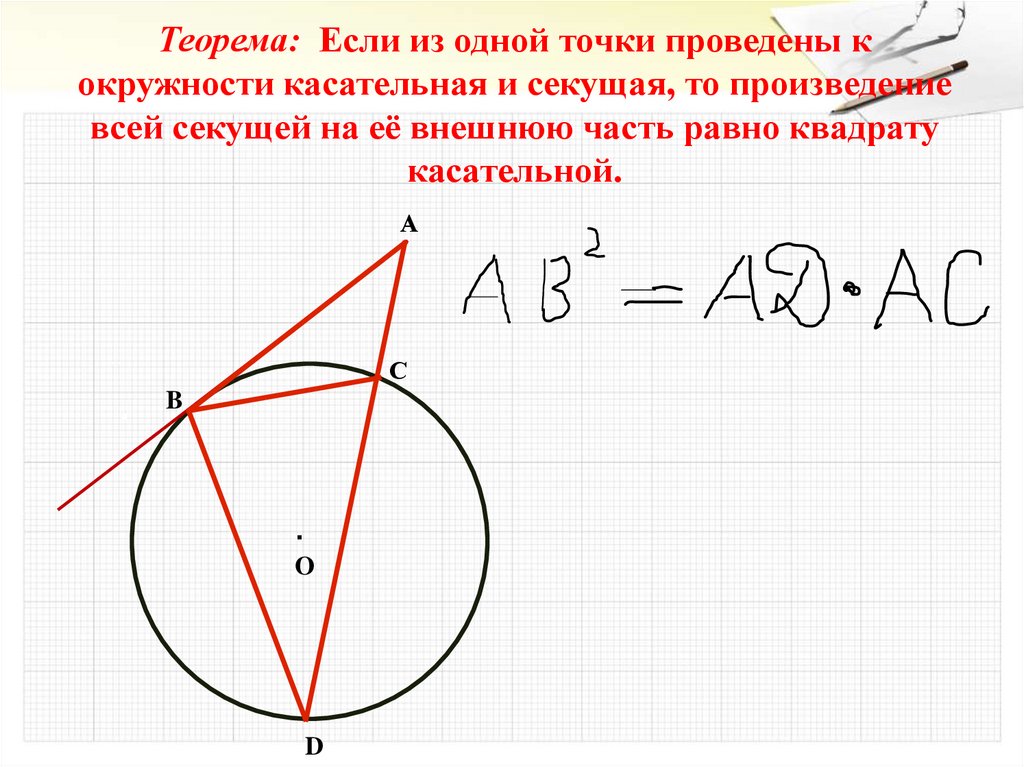
24.
Теорема: Если из одной точки проведены кокружности касательная и секущая, то произведение
всей секущей на её внешнюю часть равно квадрату
касательной.
А
...
С
. B
.
.
O
D
25.
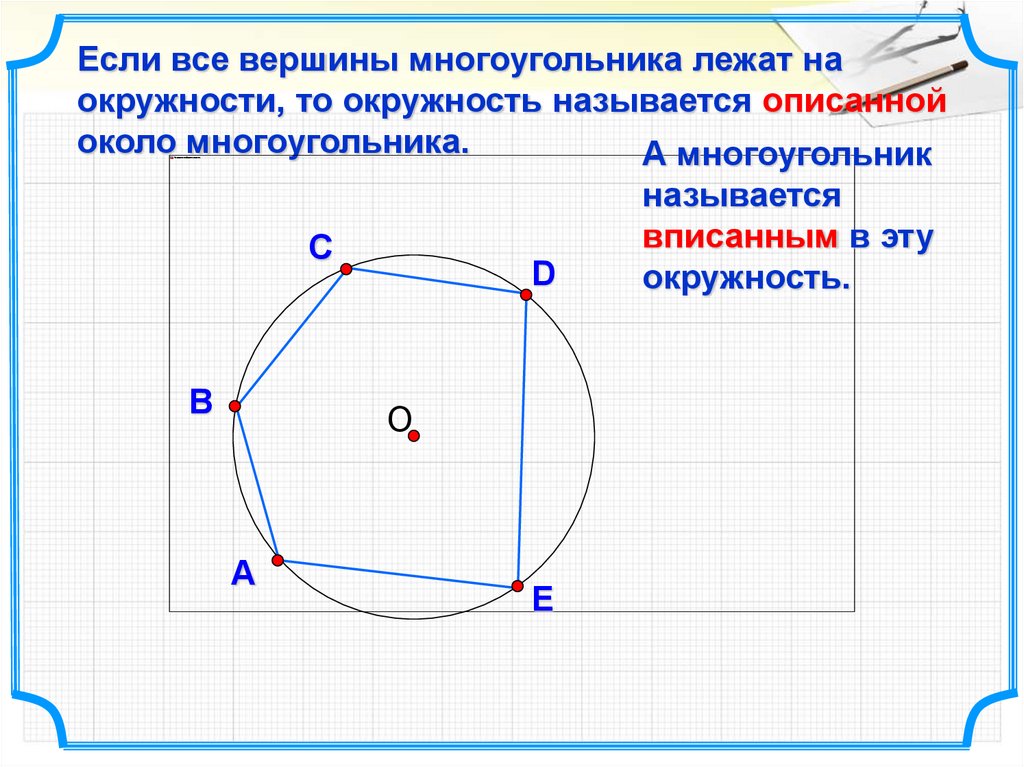
Если все вершины многоугольника лежат наокружности, то окружность называется описанной
около многоугольника.
А многоугольник
С
В
D
О
А
E
называется
вписанным в эту
окружность.
26.
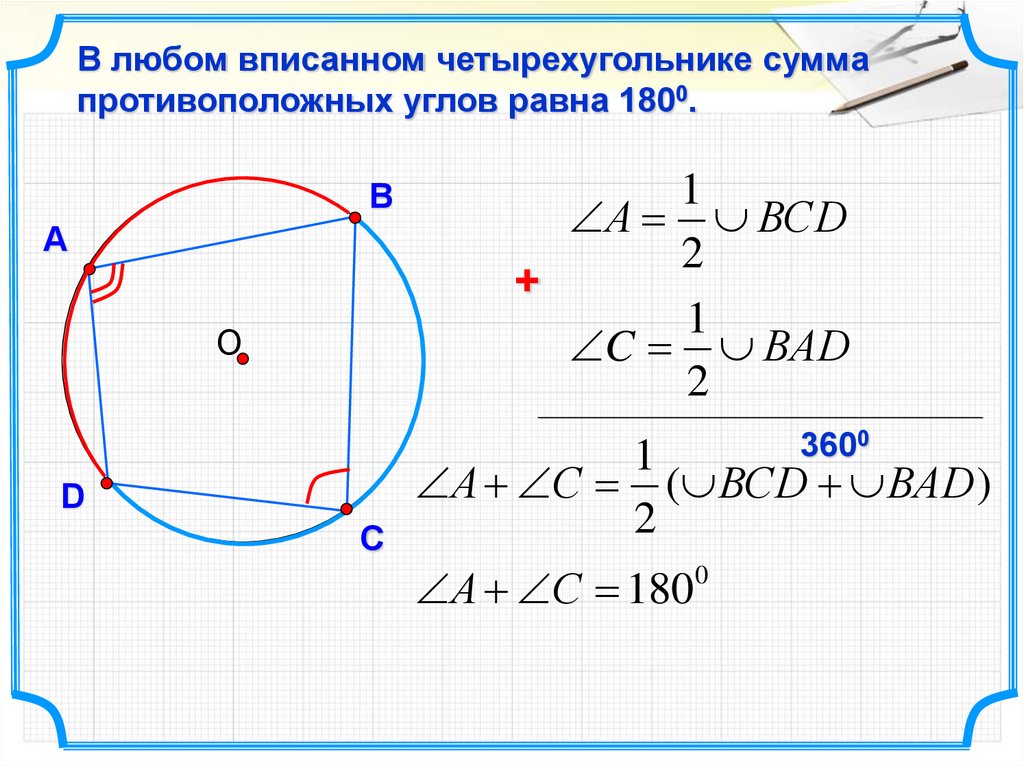
В любом вписанном четырехугольнике суммапротивоположных углов равна 1800.
В
А
О
1
А ВCD
2
+
1
C ВAD
2
3600
D
1
А С ( ВСD ВАD )
2
С
А С 1800
27.
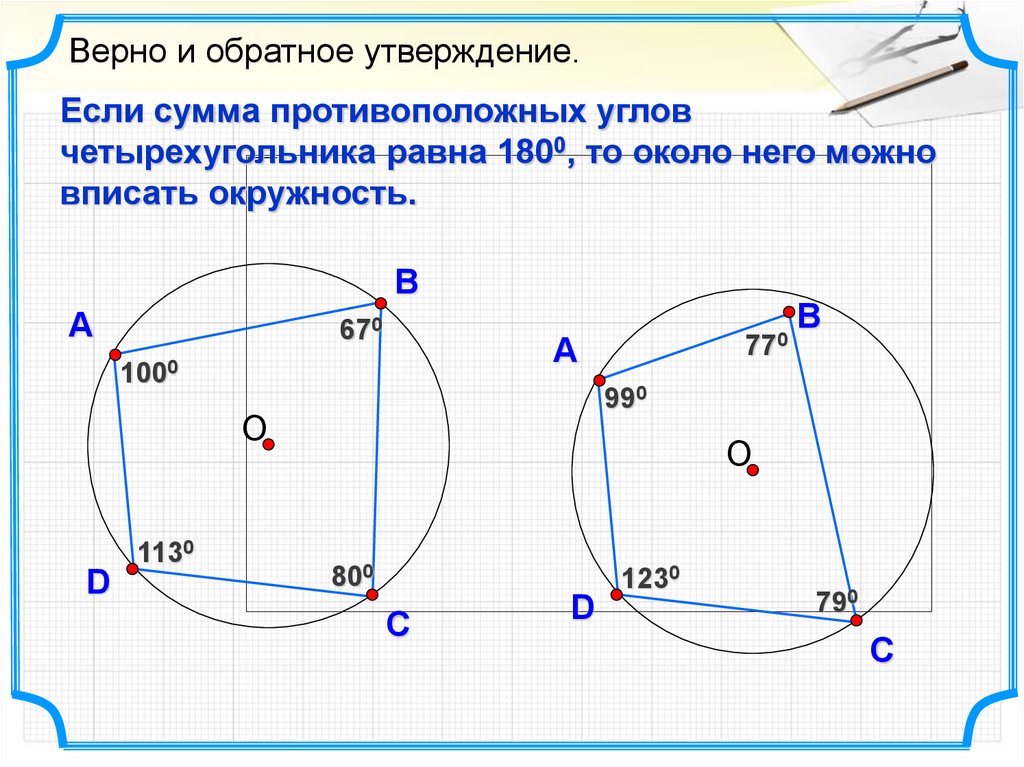
Верно и обратное утверждение.Если сумма противоположных углов
четырехугольника равна 1800, то около него можно
вписать окружность.
В
А
670
А
1000
D
В
990
О
1130
770
О
800
1230
С
D
790
С








 Математика
Математика








