Основы аэродинамики. Кинематика жидкости и газа

1.

ОСНОВЫ АЭРОДИНАМИКИ
ЛЕКЦИЯ № 2
Тема 2
Кинематика жидкости и газа

2.

Лекция № 2
Введение в кинематику жидкости и газа
Рассматриваемые вопросы:
2.1 Способы задания движения жидкости и газа.
2.2 Виды движения.
2.3 Основные термины механики сплошной среды.
2.4 Характеристики интенсивности движения.
2.5 Основные теоремы кинематики жидкости и газа.
2.6 Поле скоростей, индуцируемое вихрем.
Литература:
1. Гарбузов В. М., Ермаков А. Л., Кубланов М. С., Ципенко В. Г.
Аэромеханика: Учебник для студентов вузов гражданской авиации –
М.: МГТУГА, 2000, 288 с.
2. Логвинов И. И. Аэромеханика: Учебное пособие М.
Иркутск: ИГТУ, 1998, 144 с.
3. Ништ М. И. Аэродинамика летательных аппаратов. Учебник для
ВУЗов. М.: ВВИА им. проф. Н. Е. Жуковского, 1994, 570 с.

3.

Введение в кинематику жидкости и газа
Определения:
Кинематика жидкости – раздел гидромеханики о
видах и характеристиках движения жидкости, не
рассматривающий силы, его вызывающие.
Модель жидкости – совокупность жидких частиц,
заполняющих исследуемый объем без разрывов и
пустот.
Жидкая частица – часть жидкости, малая по
сравнению с исследуемым объёмом, но достаточно
большая, чтобы пренебречь её молекулярной
структурой.
Полюс жидкой частицы – центр её тяжести.
Виды движения жидкой частицы:
– движение полюса;
– вращение вокруг полюса;
– деформация частицы.

4.

ОСНОВНЫЕ ПОНЯТИ КИНЕМАТИКИ
Линия тока (ЛТ) – кривая, в каждой точке которой вектор скорости
направлен по касательной к ней.
Свойство ЛТ: Линии тока не пересекаются
Уравнения линии тока:
- на плоскости Oxy:
- в пространстве Oxyz:

5.

2.1 Способы задания движения жидкости и газа
2.1.1 Метод Лагранжа метод движения
однойтолько частицы из исследуемого множества.
z
Начальный момент времени t0
координаты частицы: x0, y0, z0.
Текущий момент времени координаты
частицы определены временем t:
M(t)
M(t0)
z0
x0
x f ( x0 , y0 , z0 , t );
z
y0
y
x
y
y f ( x0 , y0 , z0 , t );
z f ( x0 , y0 , z0 , t ).
Параметры Лагранжа: x0, y0, z0, t.
Проекции скорости u
x
y
z
u
;
u
;
u
;
x
y
z
и ускорения a в поле
t
t
t
системы координат по
определениям:
u y
u x
2 x
2 y
ax
; ay
;
2
2
t
t
t
t

6.

2.1.2 Метод Эйлера (движения жидкости)
Особенность метода
Изучает поля векторных или скалярных величин,
оставляя в стороне вопрос о движении каждой частицы.
Движение жидкости описывается функциями
изменения скорости в неподвижных точках
исследуемой области в пределах потока. Алгоритм:
В данный момент времени t в каждой точке
области, определяемой координатами x, y, z, находится
частица жидкости, имеющая мгновенную местную
скорость u.
Совокупность мгновенных местных скоростей
представляет векторное поле поле скоростей.

7.

Примечание к способам задания движения:
Способ принудительной генерации обтекания
неподвижного тела
Способ принудительной генерации обтекания потоком
аэродинамических тел (...) посредством силового
привода и нагнетателя (вентилятора, потока сжатого
воздуха, эжектора и ...) при неподвижном положении
аэродинамического тела (ВС, его модели, отдельных
элементов, ...) реализован в аэродинамических трубах
ЦАГИ, ВВИА им. проф. Н.Е. Жуковского, МГТУ ГА и
др.
Способ более безопасен, экономичен, но требует
изготовления дорогостоящих аэродинамических труб,
моделей, измерительных устройств, коммуникаций,
подготовки высоко квалифицированного персонала и др.

8.

.
Пример задания поля вихревого течения под
воздухозаборником ГТСУ методом стока
Для стока:
Qст
сr
2 r
Для вихря:
Г
с
.
2 r

9.

Метод Эйлера (продолжение слайда)
В общем случае поле скоростей может
изменяться по времени t и по координатам x, y, z:
Параметры “Эйлера x, y, z и t

10.

Современные способы задания течения
1 Разностный метод.
2 Метод давления.
3 Метод конечных элементов.
4 Метод ANSIS (на базе уравнений Навье и
Стокса).
5 Метод дискретных вихрей (МДВ)
С.М. Белоцерковский профессор, ДТН
(ВВИА имени проф. Н. Е. Жуковского).
6 Другие методы. ...

11.

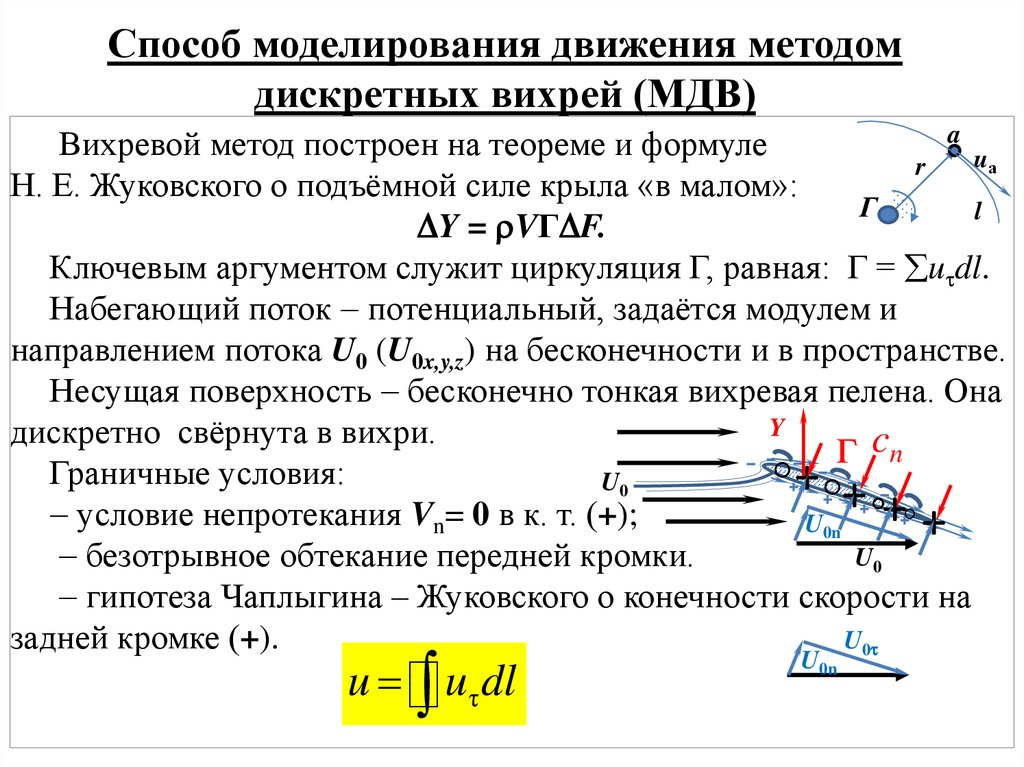
Способ моделирования движения методом
дискретных вихрей (МДВ)
a
Вихревой метод построен на теореме и формуле
uа
r
Н. Е. Жуковского о подъёмной силе крыла «в малом»:
Г
l
Y = VГ F.
Ключевым аргументом служит циркуляция Г, равная: Г = u dl.
Набегающий поток потенциальный, задаётся модулем и
направлением потока U0 (U0x,y,z) на бесконечности и в пространстве.
Несущая поверхность бесконечно тонкая вихревая пелена. Она
Y
дискретно свёрнута в вихри.
cn
г
Граничные условия:
U0
+ +
условие непротекания Vn= 0 в к. т. (+);
U0n + +
U0
безотрывное обтекание передней кромки.
гипотеза Чаплыгина – Жуковского о конечности скорости на
задней кромке (+).
U0
u uτ dl
U0n

12.

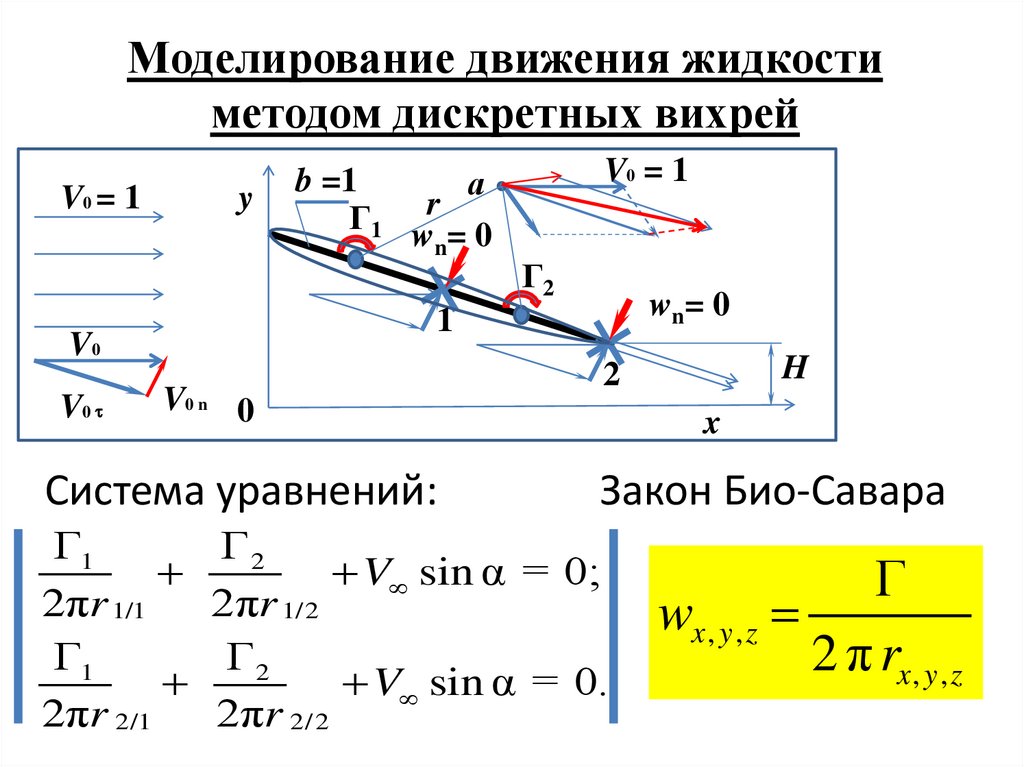
Моделирование движения жидкости
методом дискретных вихрей
V0 = 1
y
V0 = 1
а
r
wn= 0
Г2
wn= 0
1
V0
V0
b =1
Г1
V0 n 0
Система уравнений:
H
2
x
Закон Био-Савара
Г1
Г2
V sin α = 0;
2πr 1/1
2πr 1/ 2
Г1
Г2
V sin α = 0.
2πr 2/1
2πr 2/ 2
Г
wx , y , z
2 π rx , y , z

13.

2.2 Виды движения жидкости и газа
Поток (движение) жидкости и газа направленное
перемещение частиц массы вещества в пространстве с
заданными скоростью и направлением.
Различают установившиеся и неустановившиеся потоки.
Установившийся (стационарный) поток направление и
величина скорости частичек потока, их физические
параметры с течением времени не изменяются.
Неустановившийся (не стационарный) поток
направление и величина скорости частичек потока, их
физические параметры изменяются с течением времени.
По кинематике движения (отношению скоростей молекул и
потока) различают три вида течений:
турбулентное: uм > uп ;
ламинарное: uм = uп ;
кавитация
uм < uп .

14.

Краткая характеристика видов движения
Потенциальное слоистое, без признаков
углового вращения частичек среды.
Критерий потенциального течения: = 0.
Вихревое частички потока имеют угловое
вращение и отвечают критерию 0.
Установившееся течение кинематические
параметры потока не зависят от времени:
Критерий: (ux, uy, uz) f(t).
Неустановившееся течение параметры
потока зависят от времени: (ux, uy, uz) = f(t).

15.

2.3 Основные термины механики
сплошной среды и допущения
• Термины механики сплошной среды
самостоятельно!!!
• Основные допущения:
1. Среда сплошная.
2. Течение установившееся.
3. Распределение параметров газа по
исследуемому сечению равномерное.
4. Среда идеальная, невязкая.

16.

2.4 Характеристики интенсивности
движения
Интенсивность поступательного установившегося
движения оценивается скоростью u перемещения частиц
исследуемой среды.
Различают:
средняя скорость, как путь в единицу времени;
мгновенная скорость, как производную в виде предела
отношения пути ко времени при интервале времени,
стремящемся к нулю.
Интенсивность постпательного установившегося
вращения оценивается угловой скоростью , как угол
поворота частиц в единицу времени, а также ускорением,
как угловая скорость в единицу времени.
Формулы записать по ходу лекции!!!

17.

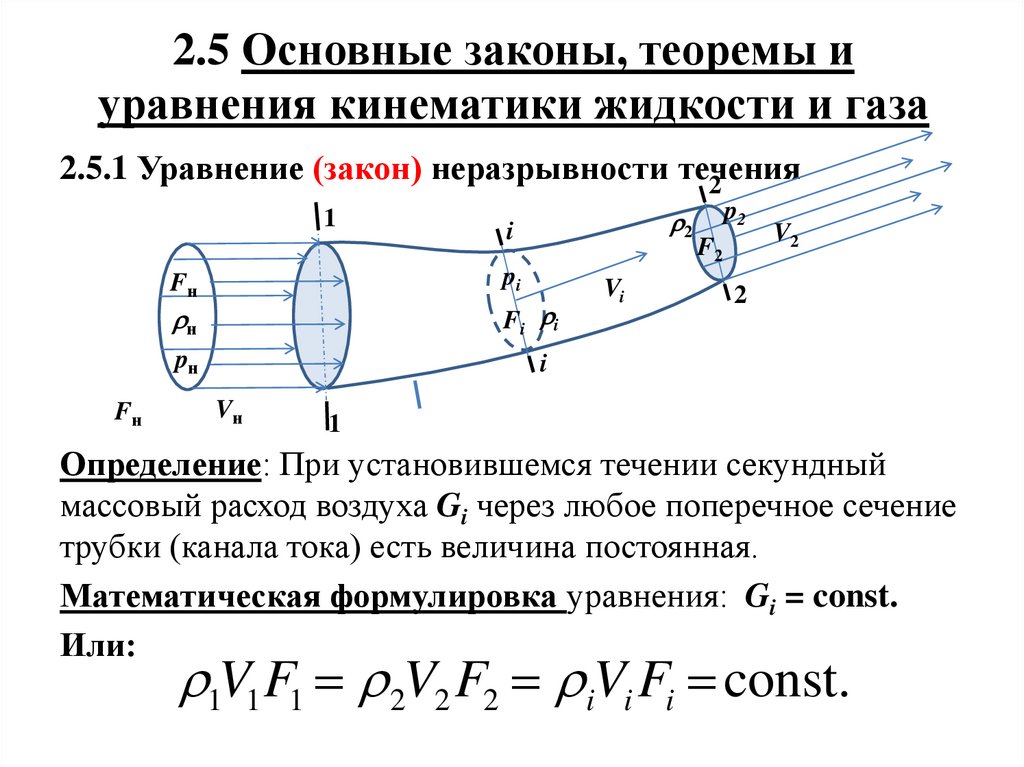
2.5 Основные законы, теоремы и
уравнения кинематики жидкости и газа
2.5.1 Уравнение (закон) неразрывности течения
2
1
i
pi
Fн
Fн
2
н
Fi i
pн
i
Vн
Vi
p2
F2
V2
2
1
Определение: При установившемся течении секундный
массовый расход воздуха Gi через любое поперечное сечение
трубки (канала тока) есть величина постоянная.
Математическая формулировка уравнения: Gi = const.
Или:
1V1 F1 2V2 F2 iVi Fi const.

18.

Основные уравнения кинематики
движения жидкости
2.5.2 Уравнение Бернулли (закон)
Определение: При установившемся течении
полное давление р* по длине
энергоизолированной трубки тока в любом
поперечном её сечение есть величина
постоянная.
Математическая формулировка уравнения:
р*i = const.
2
V
В развёрнутом виде: p* p
const.
ст
2

19.

2.6 Поле скоростей, индуцируемое вихрём
2.6.1 Закон Био-Савара для бесконечно
длинного вихря
Определения циркуляции Г:
Бытовое: Циркуляция движение аэродинамического тела по кругу.
Это определение относится к морским судам.
В авиации циркуляцию ВС по замкнутому кругу называют виражом.
Циркуляция скорости вихря представлена определением:
В поле бесконечно длинного вихря он генерирует циркуляцию
скорости Г по круговому замкнутому контуру l, равную сумме
произведения тангенциальной скорости V на длину
рассматриваемого элементарного отрезка.
По определению находим: Г = (V l).
Полагаем контур lциркуляции Г круговым и l 0, для бесконечно
длинного вихря находим:
Г Vτ dl 2 rVτ ,
где r – радиус кругового контура циркуляции.
Г
Vτ
,
Другая формулировка закона Био-Савара:
2 r τ
где – известная тригонометрическая константа.

20.

2.6.2 Закон Био-Савара для вихря
конечной длины
2
Математическое выражение:
Г
Vτ
(cos 1 cos 2 ).
4 r τ
Г
1
1
2
v
r
а
Ценным и практическим применением закона Био-Савара
являются выражения его проекций на оси выбранной системы
координат.

21.

2.6.2. Уравнение сохранения
энергии
• Определение:
Поехали!!!

22.

Уравнения Л.Эйлеера
• Вы всё знаете:
• P = m a, Н
• Известно Р t =
• Уравнение Эйлера
Определение:

23.

Теорема Н.Е. Жуковского о
подъёмной силе крыла
• Определение:
• Формула:
• Область применения:
• Подъёмная сила крыла для прикладных
исследований: