Скорость движения жидкости как сплошной среды

1. ГИДРОМЕХАНИКА

2.

Лекция 4
Плоское потенциальное
движение

3.

Скорость движения жидкости как сплошной среды
Также, как и при изучении движения твердого
тела, в кинематике жидкости при изучении
сложных явлений применяют общий принцип
разложения движений на более простые
составляющие.
Общий случай сложного движения жидкости
рассматривается состоящим из движения
элементарного объема как квазитвердого
тела, скорость которого равна сумме скоростей поступательного и вращательного движения, и деформационного движения
Это отражено в теореме Гельмгольца

4.

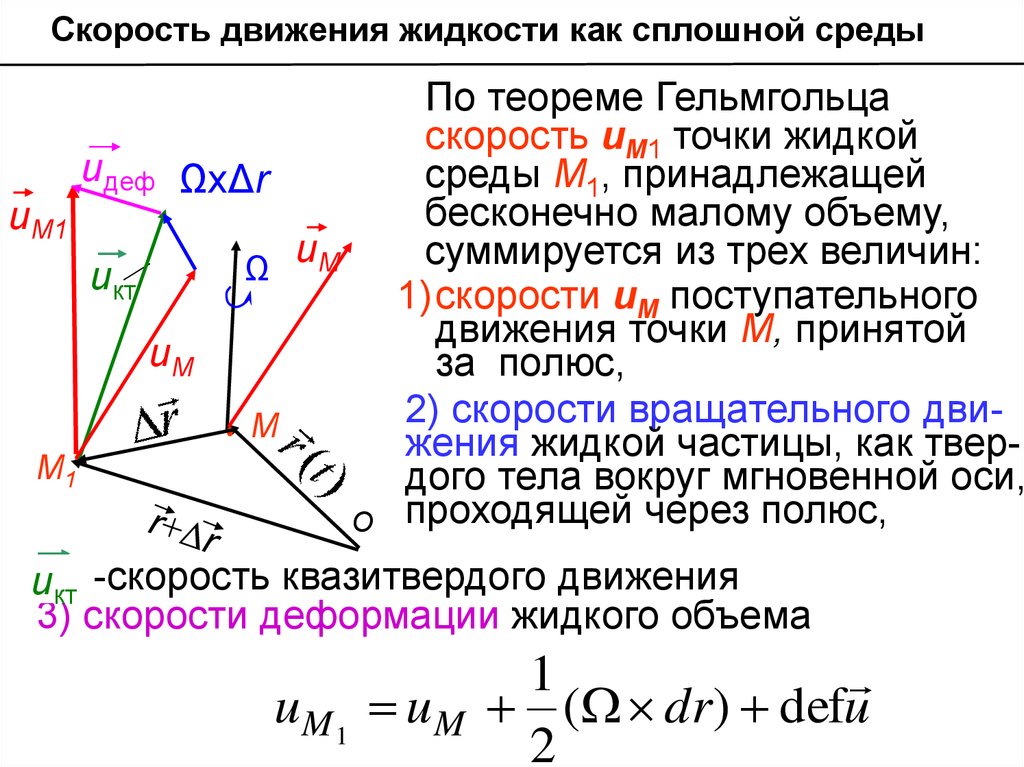
Скорость движения жидкости как сплошной среды
uМ1
uдеф ΩхΔr
uМ
Ω
uкт
uМ
М
М1
О
По теореме Гельмгольца
скорость uМ1 точки жидкой
среды М1, принадлежащей
бесконечно малому объему,
суммируется из трех величин:
1)скорости uМ поступательного
движения точки М, принятой
за полюс,
2) скорости вращательного движения жидкой частицы, как твердого тела вокруг мгновенной оси,
проходящей через полюс,
uкт -скорость квазитвердого движения
3) скорости деформации жидкого объема
uM 1 uM
1
( dr) defu
2

5.

Скорость движения жидкости как сплошной среды
Каждое составляющее движение рассматривалось подробно, так поступательное движение
изучалось с помощью линий тока и трубок тока;
вращательное движение с потоком вихря в
вихревой трубке и циркуляцией скорости;
деформационное движение, характеризовалось тензором скоростей деформаций.
Рассмотрим теперь частные случаи движений,
например, движение при отсутствии вихрей.

6.

Безвихревое (потенциальное) движение жидкости
При безвихревом движении
rotU 0,
т.е. компонеты вихря будут равны 0
u z u y
0,
y z
u x u z
0
z x
u y
u x
0
x y

7.

Безвихревое (потенциальное) движение жидкости
При выполнении этих условий линейное дифференциальное выражение
u x dx u у dy u z dz
будет полным дифференциалом некоторой
функции φ(х,y,z,t)
d u x dx u у dy u z dz
C другой стороны полный дифференциал этой
функции
d
dx
dy
dz
х
у
z

8.

Безвихревое (потенциальное) движение жидкости
Тогда
ux ;
х
uу
у
uz
z
- проекции скорости являются частными
производными функции φ по координатам. В
векторной форме это можно записать
u grad
Эту функцию φ называют потенциалом скоростей.
Безвихревое движение называют потенциальным.

9.

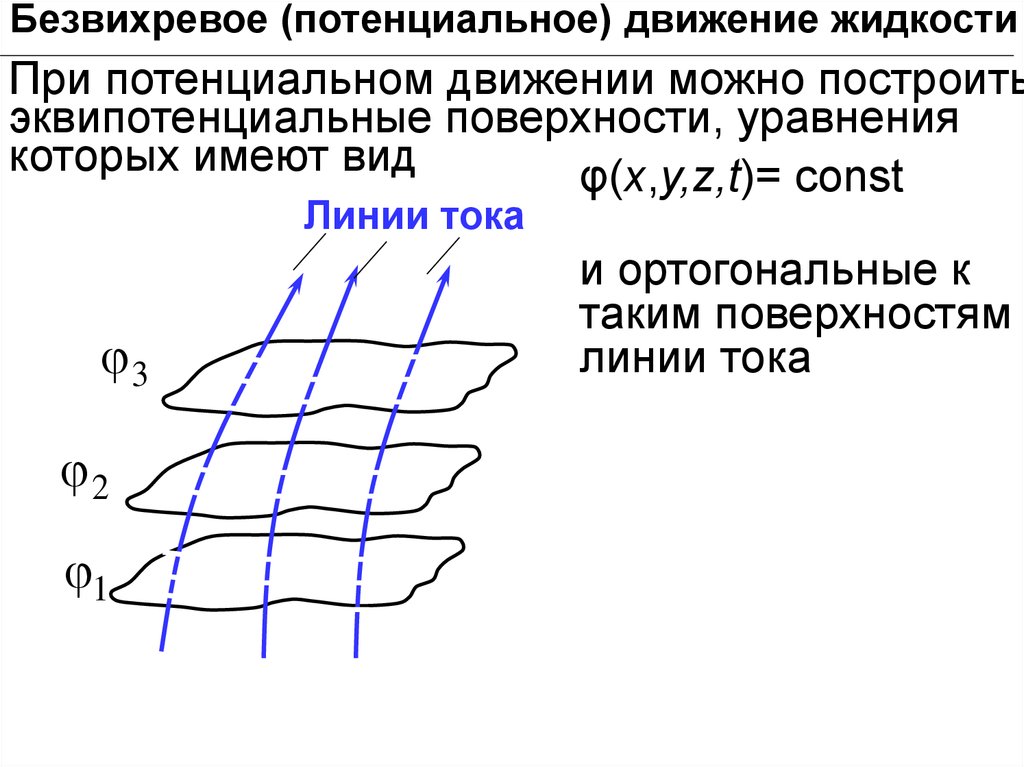
Безвихревое (потенциальное) движение жидкости
При потенциальном движении можно построить
эквипотенциальные поверхности, уравнения
которых имеют вид
φ(х,y,z,t)= сonst
Линии тока
3
2
1
и ортогональные к
таким поверхностям
линии тока

10.

Плоскопараллельное движение жидкости
Движение жидких сред в различных устройствах и машинах (в том числе в насосах и вентиляторах) можно считать плоскопараллельным.
При плоском движении траектории всех частиц
являются плоскими кривыми.
Дифференциальные уравнения Эйлера для
плоского движения можно записать
1 р du x
aх
;
ρ х
dt
1 р du у
aу
ρ у
dt

11.

Плоскопараллельное движение жидкости
Производная в правой части - это субстанциональная производная, для плоского движения
она будет выглядеть следующим образом
du x u x
u x
u x
ux
uу
;
dt
t
x
x
du y u y
u y
u y
ux
uy
dt
t
x
y
Следовательно, уравнения движения выглядят следующим образом:

12.

Плоскопараллельное движение жидкости
1 р u x
u x
u x
aх
ux
uу
;
ρ х
t
x
x
u y
u y
1 р u y
aу
ux
uy
t
ρ у
x
y
И уравнение неразрывности для плоского
движения
u x u у
0
х
у

13.

Плоскопараллельное движение жидкости
Для плоского движения потенциал скорости
– это функция φ(х,у), для которой
ux ;
х
uу
у
Плоская кривая
φ(х,у)=С
выражается эквипотенциальной линией

14.

Плоскопараллельное движение жидкости
y
Эквипотенциали
Важной практической
задачей гидромеханики
является определение
сил, действующих на
тело, обтекаемое
потоком жидкости.
x
Решение этой задачи непосредственно связано с необходимостью расчета поля скоростей,
т.е. определением проекций скоростей в
каждой его точке.

15.

Плоскопараллельное движение жидкости
При исследовании плоского потенциального
движения наряду с потенциалом скорости
большое значение имеет еще одна функция
координат, называемая функцией тока,
которая удовлетворяет условиям:
ux
;
у
uу
х
Пусть такая функция существует для некоторого потока. Тогда ее полный дифференциал
d
dx
dy u у dx u x dy
х
у

16.

Плоскопараллельное движение жидкости
Из уравнений линий тока для такого движения
можно получить
dx dy
ux u у
u у dx u x dy 0,
т.е. поле линий тока также можно представить
семейством линий тока постоянных значений:
ψ(х,у)=С

17.

Плоскопараллельное движение жидкости
Рассмотрим движение , представленное семействому линий тока
Выделим 2 линии тока
i
и
i+1
i+1
Δl
Расход жидкости, проi
текающий в элементарной
струйке
между
Δy
двумя линиями тока
yi
ψi
х
хi
Δх
их
α
иу
ψi+1
и
q=u·Δl
или
q=-uу·Δх+uх·Δу

18.

Плоскопараллельное движение жидкости
Переходя к пределу при неограниченном
сближении линий тока i и i+1
и рассматривая расход элементарной струйки
как приращение расхода всего потока при
возрастании его сечения, получим
dq= - иуdx+ ихdу.

19.

Плоскопараллельное движение жидкости
dq= - иуdx+ ихdу.
т. е.
dq=dψ
Интегрируя выражение в пределах расстояния
между двумя линиями тока, получим
Δqi+1 – Δqi = ψ2 – ψ1
или разность значений функции тока, cоответствующих двум линиям тока, равняется
расходу струи, ограниченной этими двумя
линиями токa.

20.

Плоскопараллельное движение жидкости
Потенциал скорости и функция тока взаимозависимы.
Например,
ux ;
х
uу
ux
;
у
у
uу
х
откуда
;
х у
у
х

21.

Потенциал скорости и функции тока
Линии тока и эквипотенциальные линии ортогональны между собой и совместно образуют
ортогональную сетку.
Эта сетка представляет
собой систему криволинейных прямоугольников, или, если линии построены с одинаковыми
интервалами (Δφ=Δψ), сетку криволинейных
квадратов.
Эта сетка называется гидродинамической
сеткой, или сеткой движения.

22.

Плоскопараллельное движение жидкости
Гидродинамическая сетка имеет большое
практическое значение; если она построена,
то задача о движении данного потока полностью решена.
Сетку можно строить приближенно, не зная
алгебраического выражения функций φ и ψ , а
зная только границы потока, т. е. расположение жестких неподвижных стенок, в которых
движется поток.

23.

Плоскопараллельное движение жидкости
Эти стенки являются крайними линиями тока,
между ними располагают промежуточные
линии тока
Перпендикулярно им
располагают эквипотенциали, так чтобы сетка
состояла из криволинейных квадратов.
Если средние линии в
каждом квaдpaте равны,
то построение выполнено
правильно. Так, средняя
линия а-а должна быть
равна по длине линии δ- δ.

24.

Плоскопараллельное движение жидкости
Предположим, что гидродинамическая сетка,
построена для некоторого конкретного потока,
расход которого известен.
Тогда, пользуясь этой сеткой, можно приближенно
определить скорость движения жидкости в любой
точке. Так, для точки М
скорость приближенно
иМ
Δb= δ-δ.
Q
b