Похожие презентации:
Найдите промежутки выпуклости и точки перегиба данных функций
1. Найдите промежутки выпуклости и точки перегиба данных функций:
2.
Уроки №116-118Тема урока:
Theme of the lesson:
3. Цели обучения: lesson objective:
10.4.1.33 - исследовать свойствафункции с помощью производной
и строить её график
4.
Критерии оценивания:Аssessment criteria:
- исследует функцию с помощью производной
- умеет работать по графику производной: находить
критические точки, точки экстремума и т.д.
- выполняет эскизы графиков, используя
критические точки и другие свойства
5.
6.
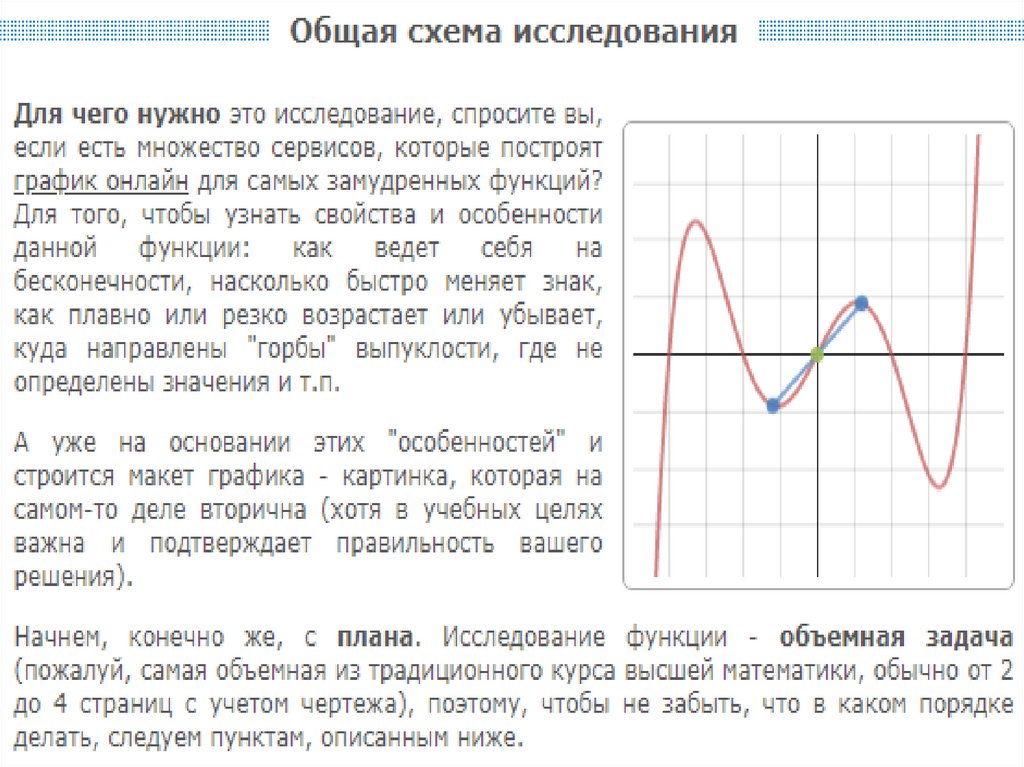
Алгоритм1. Найти область определения и множество значений. Выделить
особые точки (точки разрыва).
2. Проверить наличие вертикальных асимптот в точках разрыва и на
границах области определения. Найти наклонные (горизонтальные)
асимптоты. Исследовать поведение функции на бесконечности.
3. Найти точки пересечения с осями координат и промежутки
знакопостоянства
4. Установить, является ли функция чётной или нечётной.
5. Определить, является ли функция периодической или нет (только
для тригонометрических функций).
6. Найти точки экстремума и интервалы монотонности.
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
8. Если требуется, выбрать дополнительные точки и вычислить их
координаты.
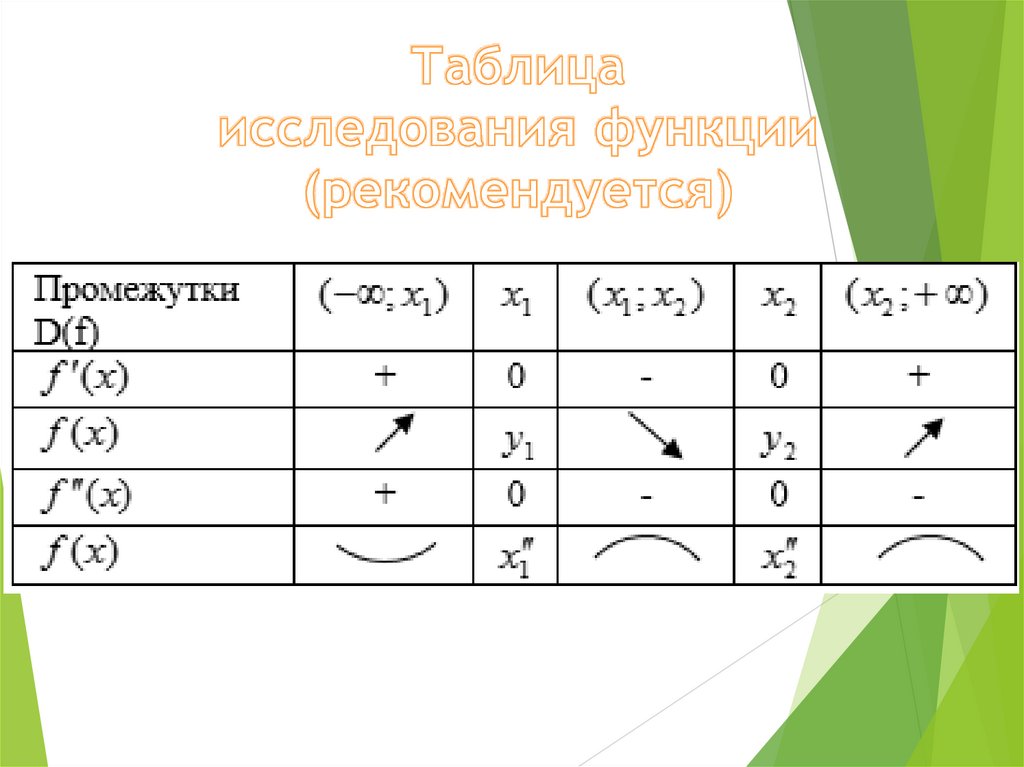
9. Оформить таблицу результатов (желательно)
10. Построить график и асимптоты.
7.
8.
Исследовать функцию и построить эскизграфика
1 x
y
2
1 x
2
9.
Находим область определения функции.Функция определена при всех значениях х,
кроме x 1
Следовательно, область определения функции
будет объединение интервалов:
1
( ; 1) ( 1;1) (1; )
2
Исследуем функцию на четность:
1 ( x) 1 x
f ( x)
f ( x)
2
2
1 ( x) 1 x
2
2
10.
Функция является четной, следовательно ееграфик будет симметричен относительно оси
ординат.
3
Находим вертикальные асимптоты.
Вертикальные асимптоты могут быть в точках
разрыва функции х =1 и х = -1.
Сначала рассмотрим точку х =1.
Если хотя бы один из пределов при
x 1
слева и справа равен бесконечности, то прямая
х =1 является вертикальной асимптотой.
11.
ПриПри
1 x2
lim
2
x 1 0 1 x
x 1
слева
x 1
1 x2
справа lim 1 x 2
x 1 0
Следовательно,
прямая
х=1
является
вертикальной асимптотой.
Аналогично можно проанализировать х=-1, но так
как
график
функции
симметричен
относительно оси ординат, то прямая х=-1
также будет вертикальной асимптотой.
4
Исследуем
поведение
функции
на
бесконечности и найдем горизонтальные и
наклонные асимптоты.
12.
1 x21
lim
2
x 1 x
1 x2
1
lim
2
x 1 x
Следовательно, y=-1 - горизонтальная асимптота.
Т.к.
f ( x)
1 x2
lim
0
lim
2
x
x
x x(1 x )
то наклонных асимптот нет.
5
Найдем
интервалы
монотонности
и
экстремумы функции.
Для этого вычислим первую производную:
1 x 2 x(1 x 2 ) ( 2 x)(1 x 2 )
y
2
2 2
(1 x )
1 x
2
13.
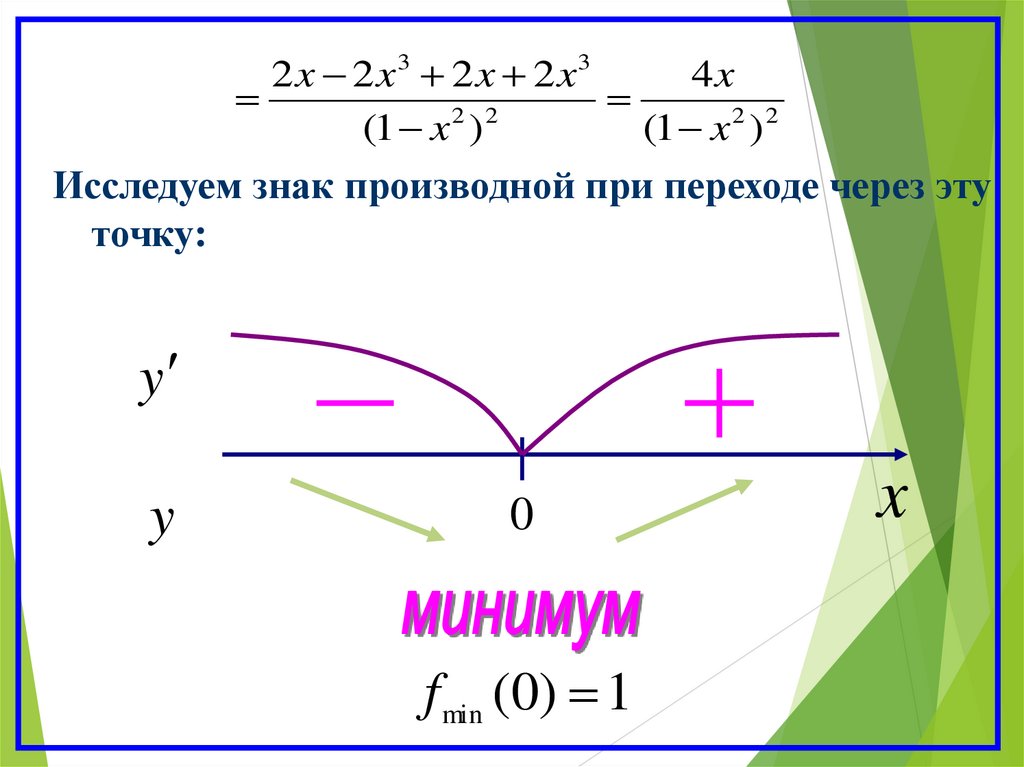
2 x 2 x3 2 x 2 x34x
2 2
(1 x )
(1 x 2 ) 2
Исследуем знак производной при переходе через эту
точку:
y
y
0
f min (0) 1
x
14.
Интервалы монотонности функции:Функция убывает на: ( ; 1) ( 1;0)
Функция возрастает на: (0;1) (1; )
6
Найдем интервалы выпуклости и точки
перегиба.
Для этого вычислим вторую производную:
2 2
2 2
4 x (4 x) (1 x ) 4 x (1 x )
y
2 2
2 4
(1 x )
(1 x )
4 (1 x 2 ) 2 4 x 2(1 x 2 ) ( 2 x) 4 4 x 2 16 x 2
2 4
2 3
(1 x )
(1 x )
15.
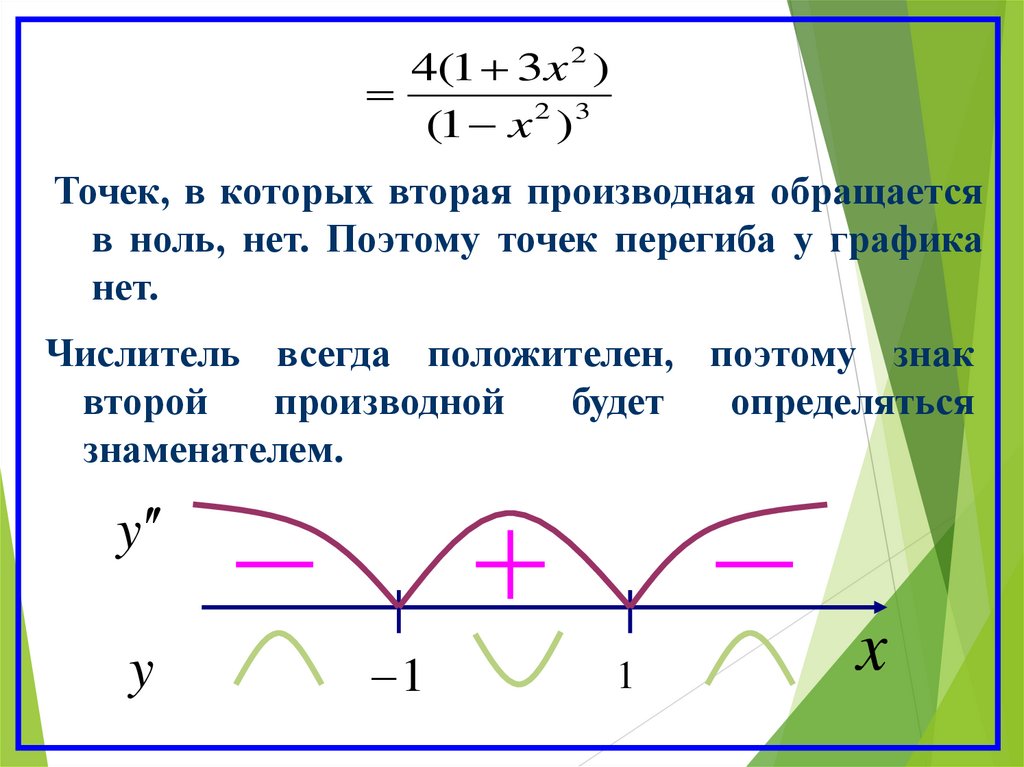
4(1 3x 2 )(1 x 2 )3
Точек, в которых вторая производная обращается
в ноль, нет. Поэтому точек перегиба у графика
нет.
Числитель всегда положителен, поэтому знак
второй
производной
будет
определяться
знаменателем.
y
y
1
1
x
16.
Интервалы выпуклости функции:Функция выпукла вниз на: ( 1 ; 1)
Функция выпукла вверх на: ( ; 1) (1; )
7 Найдем точки пересечения графика функции с
осями координат:
При x 0
1 0
y
1
1 0
(0,1) - точка пересечения с осью ординат.
Точек пересечения с осью абсцисс нет.
8 Строим график функции:
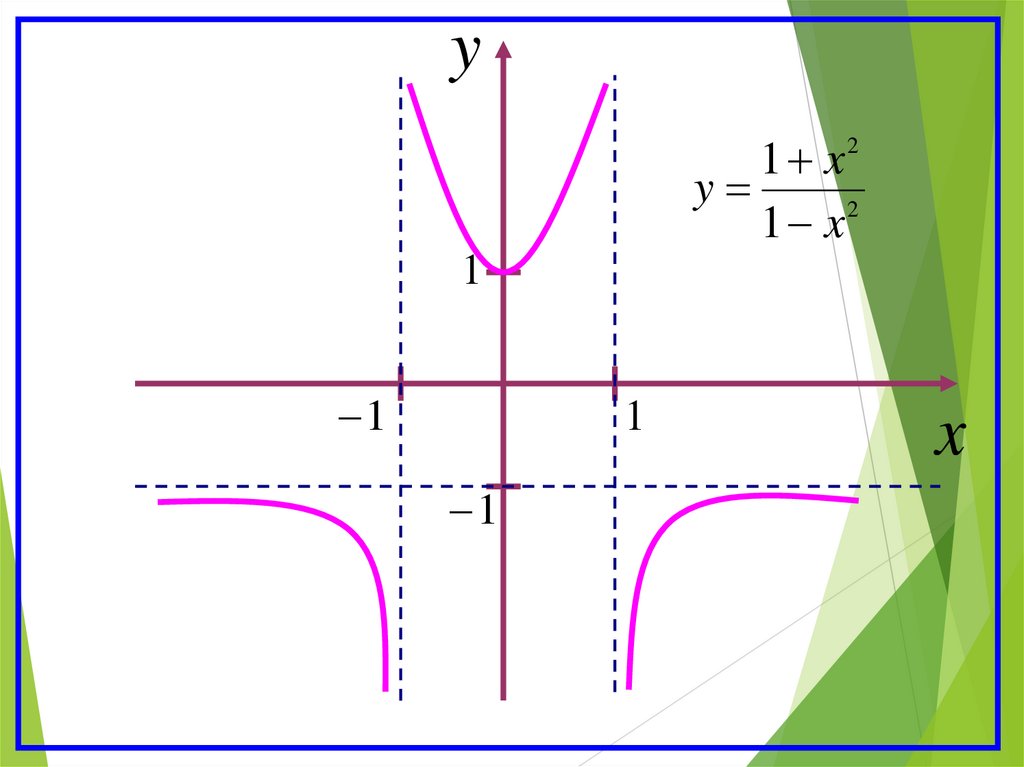
17.
y1 x2
y
1 x2
1
1
1
1
x
18. Задачи 1-4
Исследовать функцию и построить эскиз графика:y 3х 16 х 24 х 9
4
3
3
2
2
x
x
1) f ( x)
2х 3
3
2
1 x
2) y
х 1
2
4
3) y х
х
19.
20.
ReflectionБыло не понятно
Не
уверен в
себе
Все понятно
21.
https://bilimland.kz/ru/subject/algebra/10-klass/issledovanie-funkczii-spomoshyu-proizvodnoj-i-postroenie-eegrafika?mid=003b8930-9d5a-11e9-be7849d30a05e051













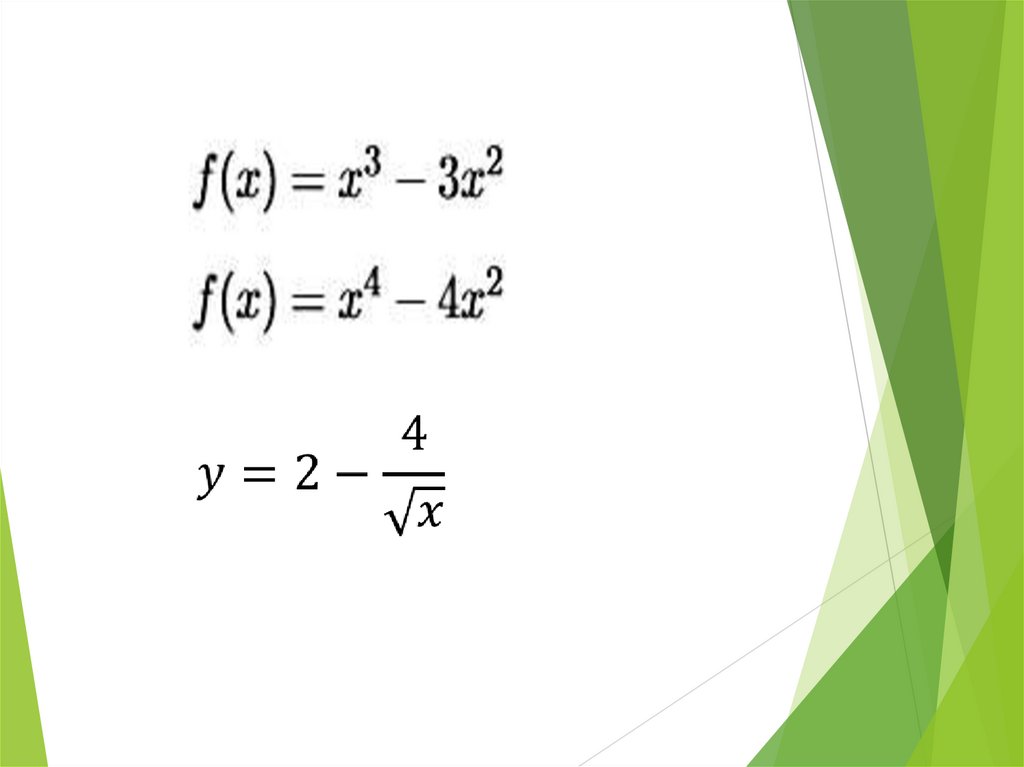


 Математика
Математика








