Преобразования графиков функций

1.

Преобразования
графиков функций — это
линейные преобразования
функции y = f(x) или её
аргумента x к виду y = af(kx +
b) + m, а также преобразование
с использованием модуля.

2.

Различают три вида геометрических
преобразований графика функции:
➲Первый
вид - масштабирование (сжатие или растяжение)
вдоль осей абсцисс и ординат.
➲То, что требуется выполнить масштабирование, показывают
коэффициенты k1 и k2 в уравнении y = ± k1 f (± k2 (x + a))+b.
Они должны быть не равны единице.
➲Когда 0 < k1,2 <1, совершаем сжатие графика относительно 0y
и растяжение относительно 0x , когда k1,2>1, выполняем
растяжение вдоль оси ординат и сжатие вдоль оси абсцисс.

3.

➲Когда
функция принимает вид y = f (k2x) ,то
если k2 >1 – производим сжатие графика к
оси ординат (0y) в k раз, а если 0 < k2<1 растяжение графика от оси ординат в 1/k.
Когда функция принимает вид y = k1 f (x) , то

4.

Второй вид - симметричное (зеркальное)
отображение относительно координатных осей.
➲Этот
тип преобразований
необходимо проводить в случаем,
когда присутствует «минус» перед
коэффициентами k1,
(симметрично отображаем график
относительно оси ox ) и k2
(симметрично отображаем график
относительно оси oy). Когда знак
«минус» отсутствует, то этот этап
пропускается.
➲
другими словами:
➲Когда
функция принимает вид y = f (-x)
выполняем симметричное отражение
графика относительно оси ординат (0у).
➲Когда
функция принимает вид y = - f (x)
выполняем симметричное отражение
графика относительно оси абсцисс (0х).

5.

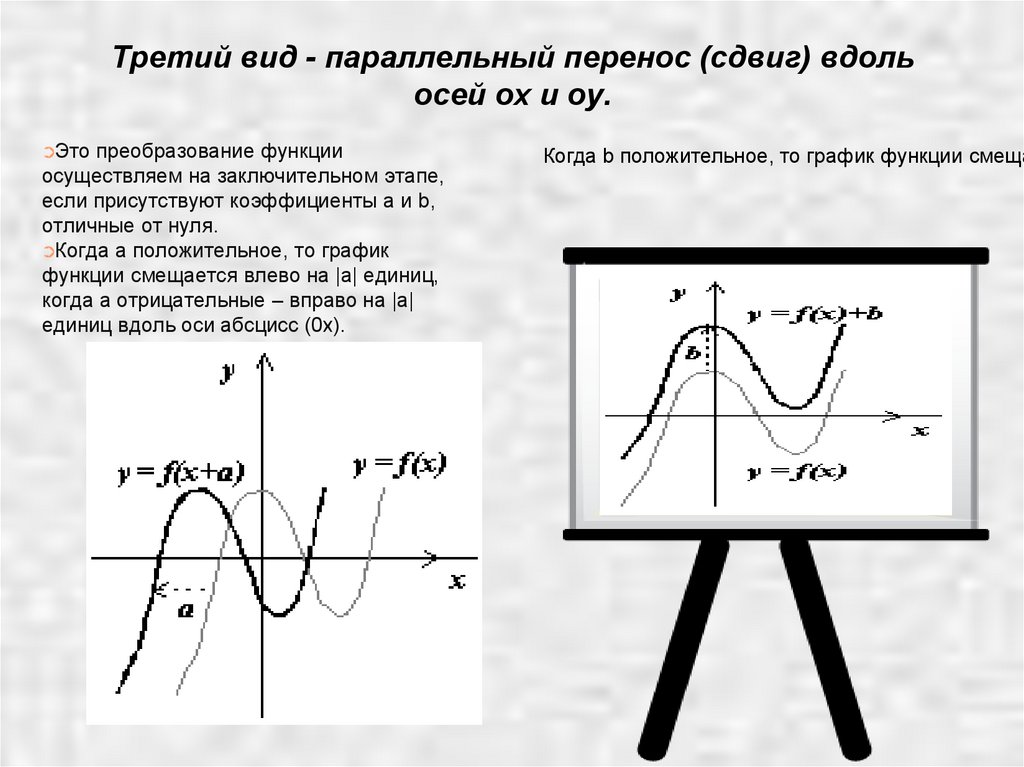
Третий вид - параллельный перенос (сдвиг) вдоль
осей ox и oy.
➲Это
преобразование функции
осуществляем на заключительном этапе,
если присутствуют коэффициенты a и b,
отличные от нуля.
➲Когда а положительное, то график
функции смещается влево на |а| единиц,
когда а отрицательные – вправо на |а|
единиц вдоль оси абсцисс (0х).
Когда b положительное, то график функции смеща

6.

7.

8.

Зная, как строить графики функции y = f(x), где y = kx + b, y = ax2, y = xn , y=xk, y = sin x, y = co
Параллельный перенос графика вдоль оси абсцисс на | b | единиц
в
право, если b > 0;
влево, если b < 0.
y = f(x + b)
влево, если b > 0;
вправо, если b y = f(x - b)
Параллельный перенос графика вдоль оси абсцисс на | b | единиц
в< 0.
y = f(x) + m
Параллельный перенос графика вдоль оси ординат на | m | единиц
вверх, если m > 0,
вниз, если m < 0.
Отражение графика
y = f( - x)
Симметричное отражение графика относительно оси ординат.
y = - f(x)
Симметричное отражение графика относительно оси абсцисс.
Сжатие и растяжение графика
y = f(kx)
При k > 1 — сжатие графика к оси ординат в k раз,
при 0 < k < 1 — растяжение графика от оси ординат в k раз.
y = kf(x)
При k > 1 — растяжение графика от оси абсцисс в k раз,
при 0 < k < 1 — cжатие графика к оси абсцисс в k раз.
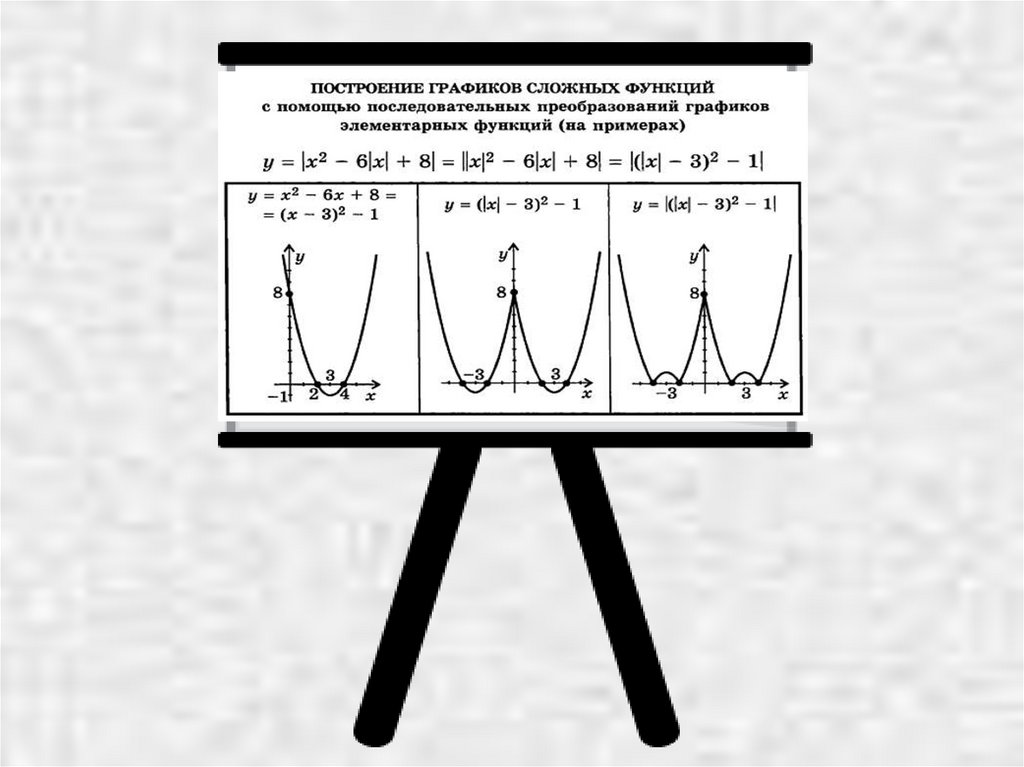
Преобразования графика с модулем
y = | f(x) |
При f(x) > 0 — график остаётся без изменений,
при f(x) < 0 — график симметрично отражается относительно оси абсцисс.
y = f( | x | )
При x0 — график остаётся без изменений,
при x < 0 — график симметрично отражается относительно оси ординат.