Похожие презентации:
Первообразная и интеграл. Взаимно-обратные операции
1.
Первообразная и интеграл2.
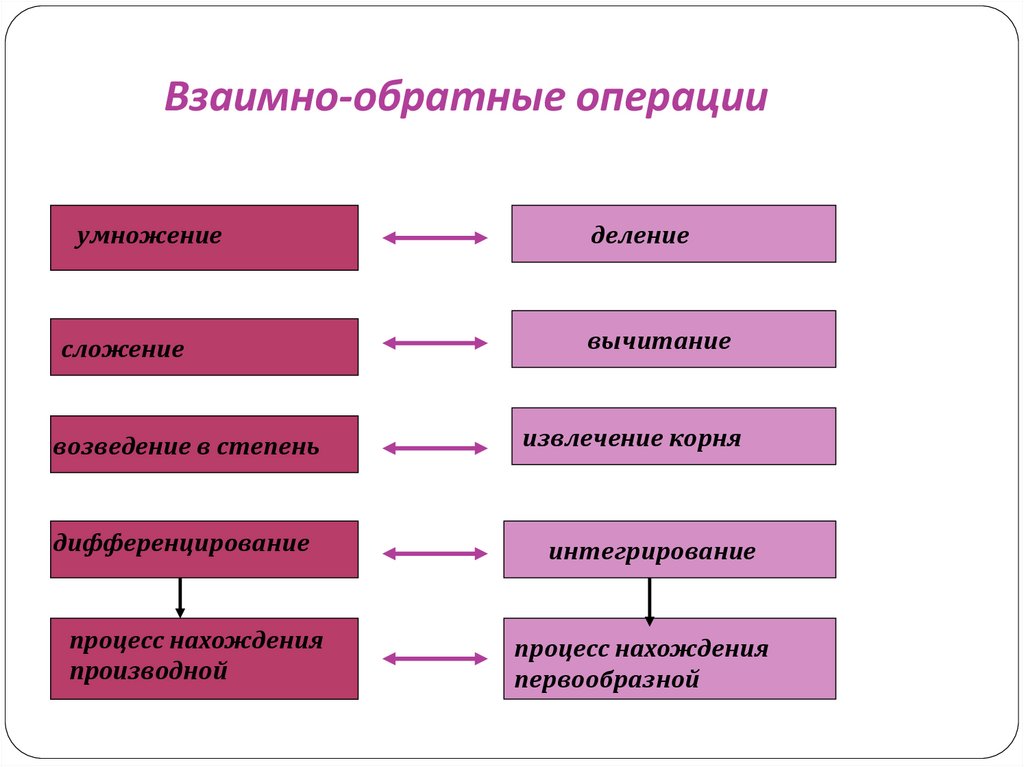
Взаимно-обратные операцииумножение
деление
сложение
вычитание
возведение в степень
извлечение корня
дифференцирование
интегрирование
процесс нахождения
производной
процесс нахождения
первообразной
3.
Определение первообразнойПервообразной для функции f(x) называется
функция, производная которой равна данной
Функция F(x) называется первообразной для
функции f(x) на промежутке I ,если для
любого х из промежутка I выполняется
F x f x
равенство:
Пример:
Первообразной для функции f(x)=x на всей числовой
оси является F(x)=x2/2, поскольку (x2/2)’=x.
4.
Таблица первообразных некоторыхфункций
k
х
F (x) kx
x n 1
n 1
f (x)
n
1
х
sin x
cos x
2 х
cos x
sin x
5.
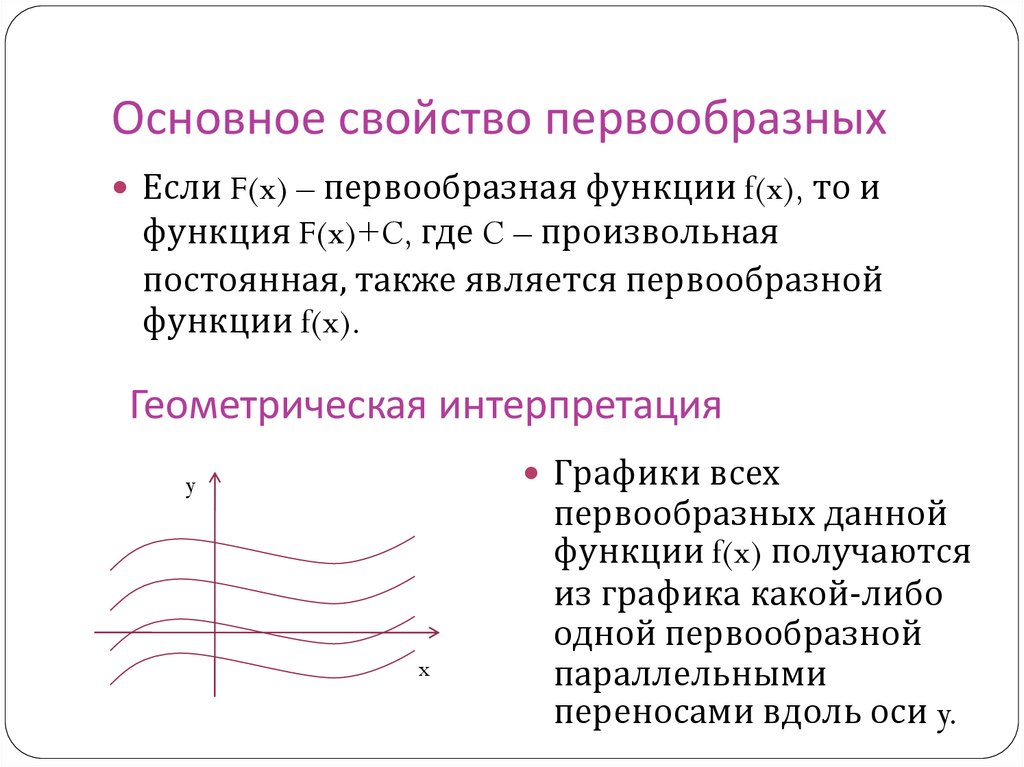
Основное свойство первообразныхЕсли F(x) – первообразная функции f(x), то и
функция F(x)+C, где C – произвольная
постоянная, также является первообразной
функции f(x).
Геометрическая интерпретация
Графики всех
y
x
первообразных данной
функции f(x) получаются
из графика какой-либо
одной первообразной
параллельными
переносами вдоль оси y.
6.
Найти производную функции F(x):1 ряд
F ( x) x 4 20
2 ряд
F x x 4 0,25
3 ряд
F x x 4 100
пусть _ F x f x
3
4х
f x
f x 4х 3
f x 4х 3
Вывод: для данной функции существует множество первообразных, их
можно записать в виде F(x)+C
Основная задача интегрирования: записать все первообразные для
данной функции. Решить её- значит представить первообразную в
таком общем виде: F(x)+C








 Математика
Математика








