Понятие первообразной. Взаимно - обратные операции в математике

1.

Автор: преподаватель
математики Князева И.Е.

2.

Цели урока:
Сформировать
представление
о
понятии
"первообразная", способствовать формированию умений
применять полученные знания в новой ситуации.
Установить связь между производной и первообразной,
формировать умение проверять является ли данная
функция первообразной для другой, заданной на
некотором числовом промежутке функции.
Развивать навыки мыслительной деятельности при
анализе и структурировании учебного материала
Способствовать привитию культуры умственного труда,
воспитывать организованность и сосредоточенность

3.

Найти первоначальную функцию,
если известна ее производная

4.

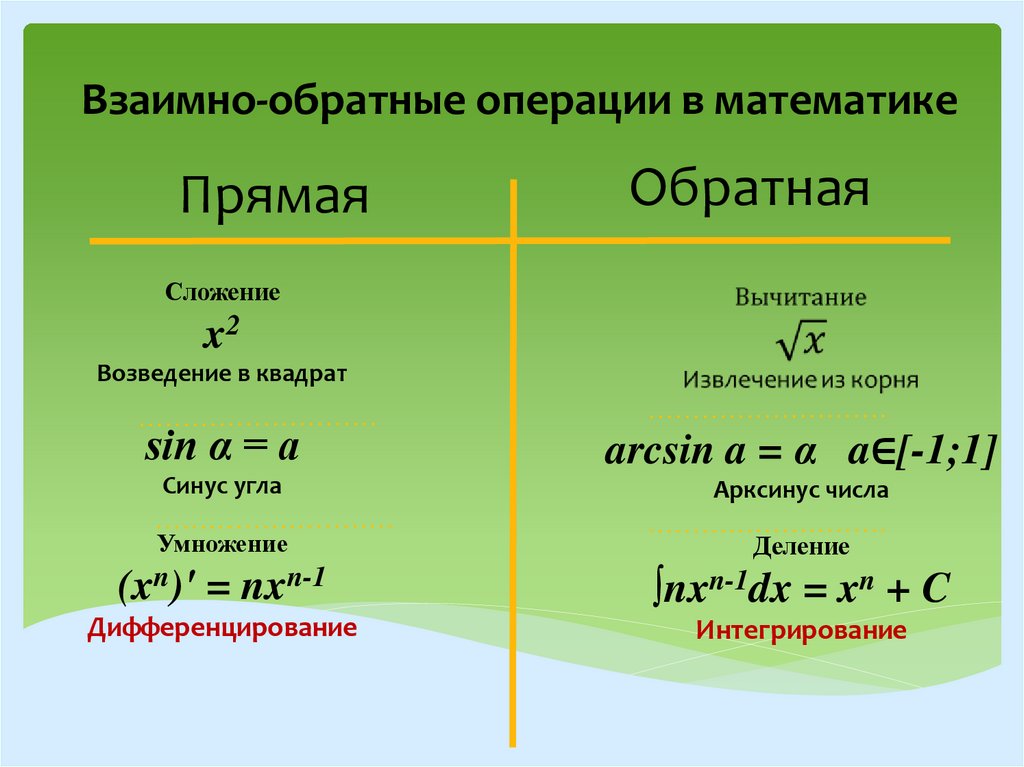
Взаимно-обратные операции в математике
Прямая
Обратная
Сложение
x2
Возведение в квадрат
sin α = a
arcsin a = α a∈[-1;1]
Синус угла
Арксинус числа
Умножение
Деление
(xn)' = nxn-1
∫nxn-1dx = xn + C
Дифференцирование
Интегрирование

5.

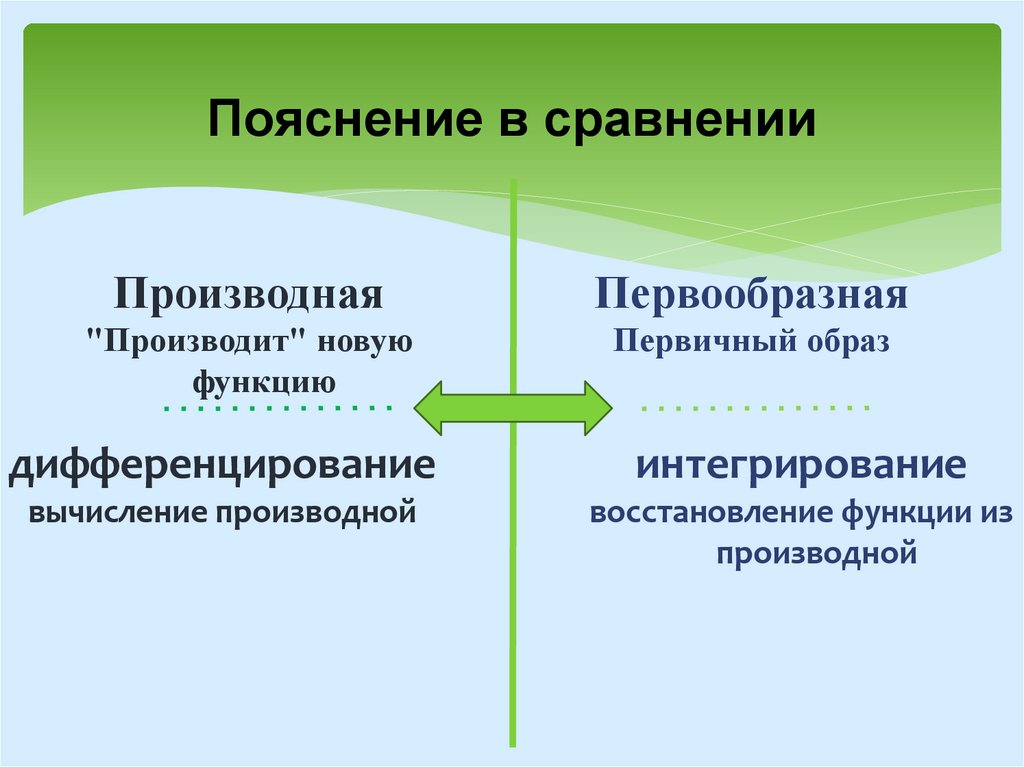
Пояснение в сравнении
Производная
Первообразная
"Производит" новую
функцию
Первичный образ
дифференцирование
интегрирование
вычисление производной
восстановление функции из
производной

6.

Определение первообразной
y = F(x) называют первообразной для y = f(x) на
промежутке X, если при x ∈ X
F'(x) = f(x)

7.

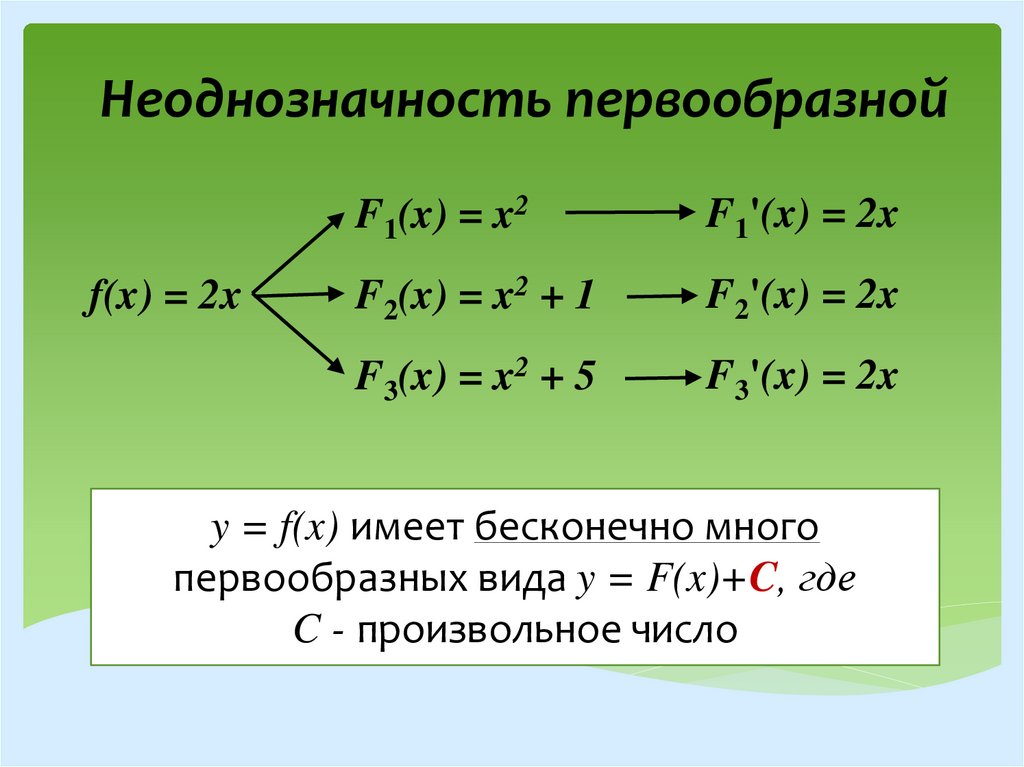
Неоднозначность первообразной
f(x) = 2x
F1(x) = x2
F1'(x) = 2x
F2(x) = x2 + 1
F2'(x) = 2x
F3(x) = x2 + 5
F3'(x) = 2x
y = f(x) имеет бесконечно много
первообразных вида y = F(x)+C, где
C - произвольное число

8.

Таблица первообразных
f(x)
F(x)
1
k
kx+C

9.

Правила интегрирования

10.

Задача

11.

Аналогично выполните для
f(x)= 2х
2х
F(x) =
+с
ln 2

12.

1.Первообразная для функции f(x) =х+