Показательные неравенства

1. «Показательные неравенства»

2.

Показательные
неравенства
Определение
Простейшие
неравенства
Решение неравенств

3. Определение

Показательные неравенства –
это неравенства, в которых
неизвестное содержится в
показателе степени.
Примеры:
3 9;
х
2 5 2
х
х 1
11

4. Виды неравенств

Линейное нер-во
2х+7>0
-8х+4<0
Квадратное нер-
во
х^2-4х+3>0

5. Простейшие показательные неравенства – это неравенства вида:

a a
b
a a
b
x
x
a a
x
b
a a
x
b
где a > 0, a 1, b – любое число.

6.

При решении простейших
неравенств используют свойства
возрастания или убывания
показательной функции.
a a
x b
a 1
x
b
a a
x b
0 a 1
x
b

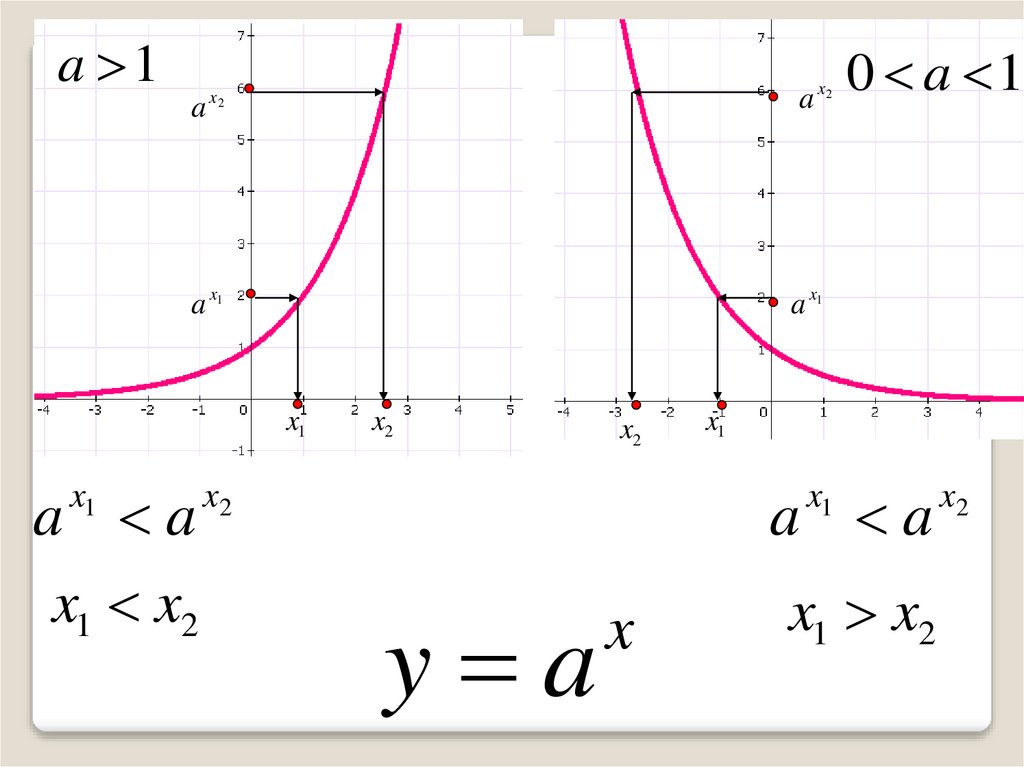
7.

a 1
x2
a x2
a x1
a x1
a
x1
a a
x1 x2
x1
x2
x2
0 a 1
x1
a a
x2
x1
y a
x
x1 x2
x2

8. Какие из перечисленных функций являются возрастающими, а какие убывающими?

1) y 5
x
возрастающая, т.к.5 1
2) y 0,5 убывающая, т.к.0 0,5 1
x
3) y 10
4) y
x
x
возрастающая, т.к.10 1
возрастающая, т.к. 1

9. Какие из функций являются возрастающими, а какие убывающими?

2
5) y
3
x
6) y 49
2
убывающая, т.к.0 1
3
x
1
1
убывающая, т.к.49 и 0
1
49
49
1

10. При а>1 функция возрастает

При а>1 функция возрастает
a
x x
a
x
a
x x
x0
a
0
x
x0
0
При 0<а<1 функция убывает
x
x
x
x
a
a
a
a
x x
0
0
x x
0
0

11.

Решения показательных
неравенств:
1. Способ Уравнивание оснований правой
и левой части

12. Решите неравенство:

3 81
x
4
3 3
x
т.к.3 1, то функция y 3 возрастающая
x
x 4
x 4;

13. Решите неравенство:

x
1 1
2 2
3
2
x
1
т.к.0 1, то функция y убывающая
2
2
1
3
x
2
3
x - ;
2

14.

Решите неравенство:
1
2 ;
2
3x
1
2 2 ;
3x
т.к. основание 2 1, то функция возрастающая
3 x 1;
1
x ;
3
1
x ;
3

15.

Простейшие показательные неравенства
Неравенства, решаемые вынесением за
скобки степени с меньшим показателем
Неравенства, решаемые введение новой
переменной

16. Простейшие показательные неравенства

1). 3 9 3 x 32 x 2
х
Ответ : х 2.
1
1
1
2).
4
2
2
х
Ответ : х 2.
x
2
1
x 2
2

17. Решение показательных неравенств

Способ 2: Вынесение за скобки степени с
меньшим показателем
1 х
х 3
3 3 10
3
3
х 3
3
3
1 3
(1 3 ) 10
3
х 3
х 3
(1 9) 10
10 10 : 10
х 3
1
х 3
0
3
3
3 > 1, то х 3 0
3
х 3.
Ответ: х >3

18. Решение показательных неравенств

Способ 3: введение новой переменной
(t 9) t 1 0
9 10 3 9
х
х
3 10 3 9 0
2х
х
3 t (t 0)
х
1 t 9
t 2 10t 9 0
D 10 4 9 100 36 64 8
2
10 8 18
t1
9
2
2
10 8 2
t2
1
2
2
1 3x 9
2
3 3 ; 3 3 ;
х
2
х 2
х
0
х 0.
3>1, то
Ответ: х < 2. х>0