Похожие презентации:
Подобие треугольников
1. Подобие треугольников
Урок - практикум2. Найдите подобные треугольники и обоснуйте их подобие.
12
4
6
3
5
7
9
8
10
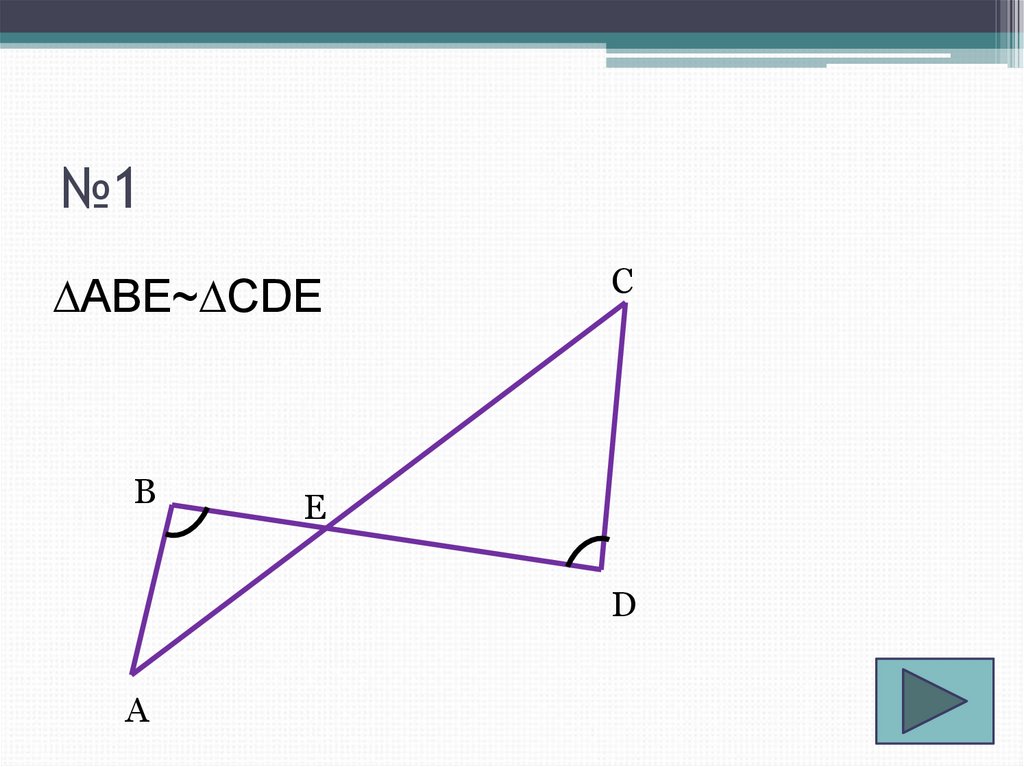
3. №1
∆ABE~∆CDEВ
С
Е
D
А
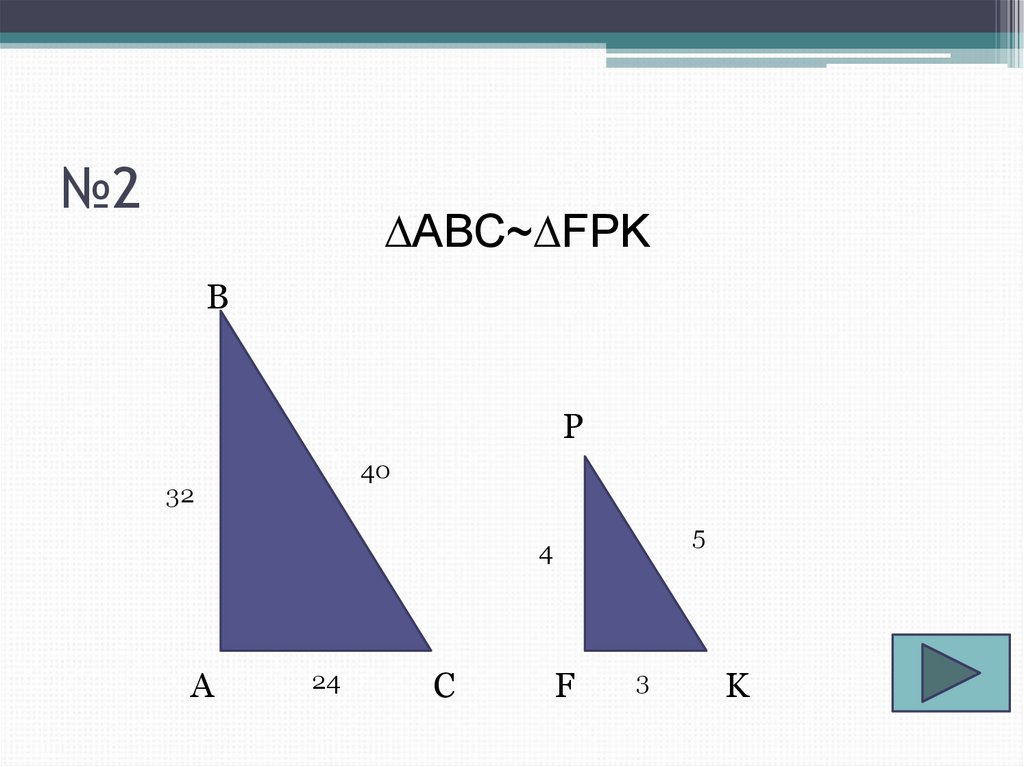
4. №2
∆ABC~∆FPKB
P
40
32
5
4
А
24
C
F
3
K
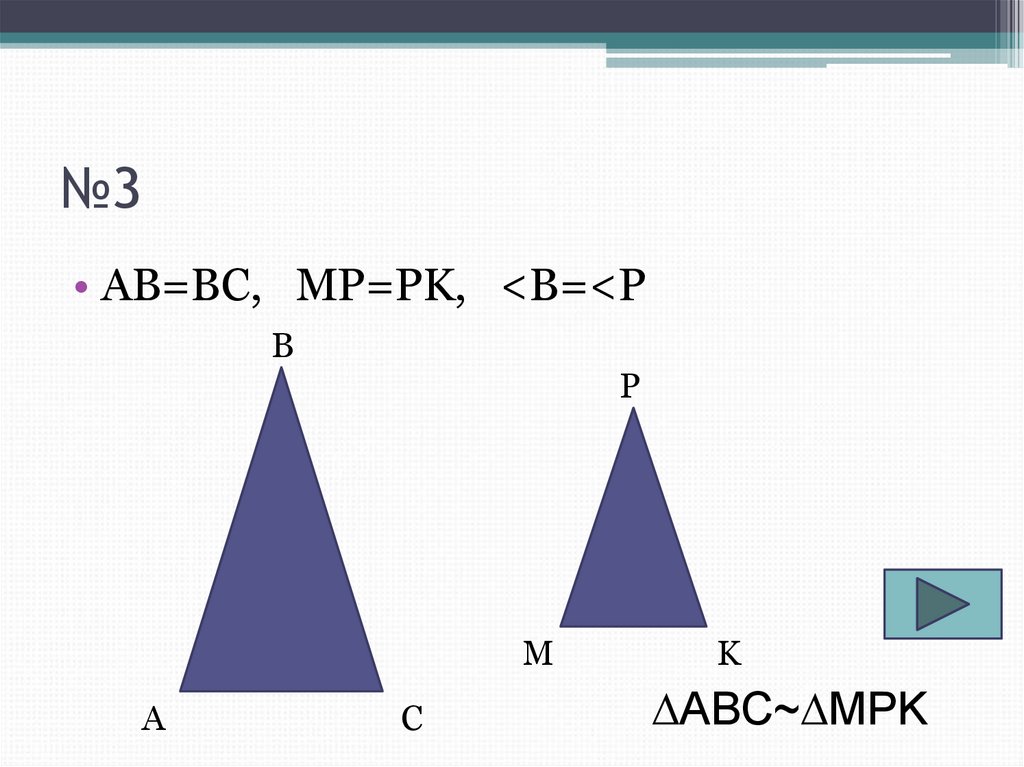
5. №3
• AB=BC, MP=PK, <B=<PB
P
M
A
C
K
∆ABC~∆MPK
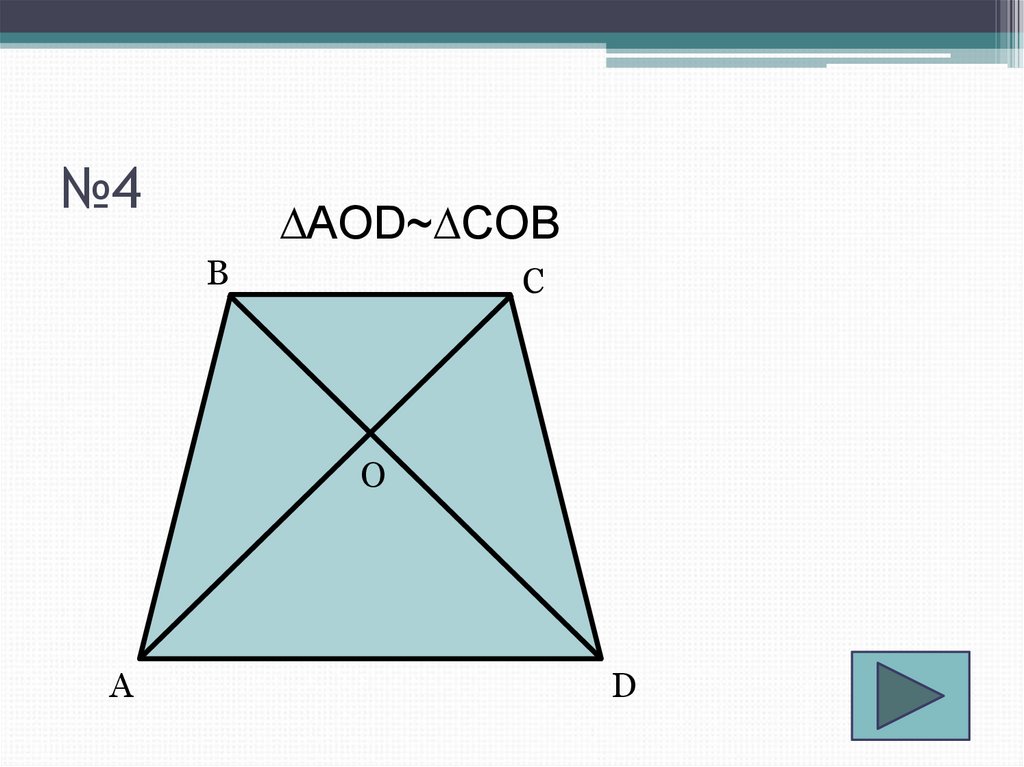
6. №4
∆AOD~∆COBB
C
O
A
D
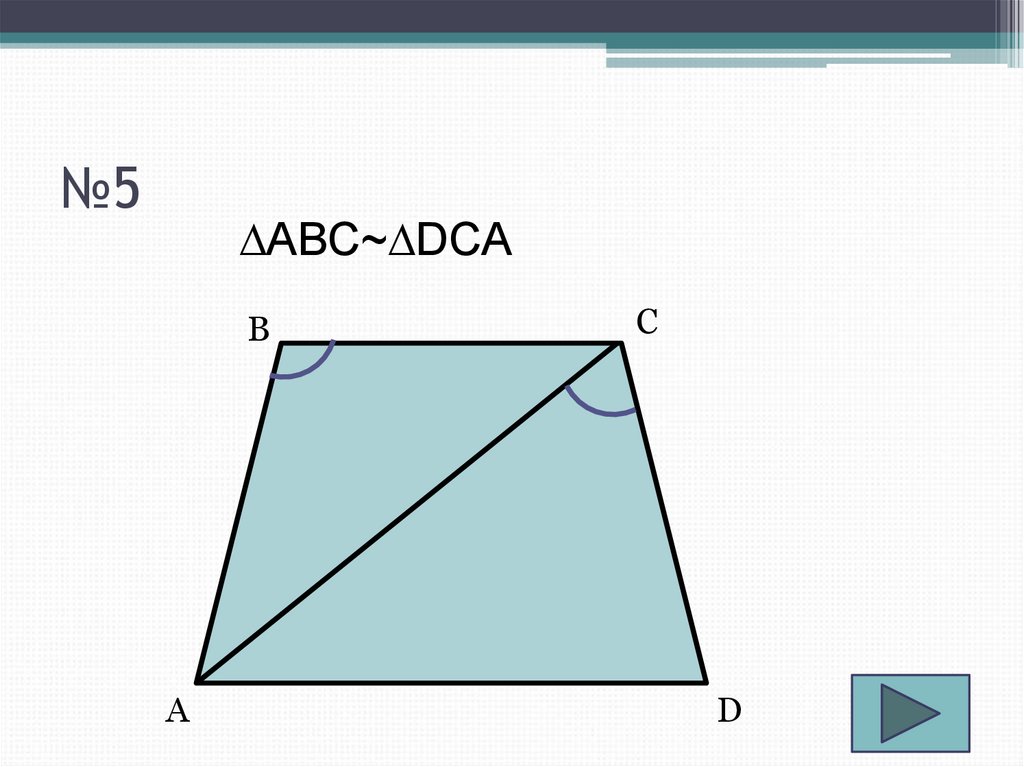
7. №5
∆ABC~∆DCAB
A
C
D
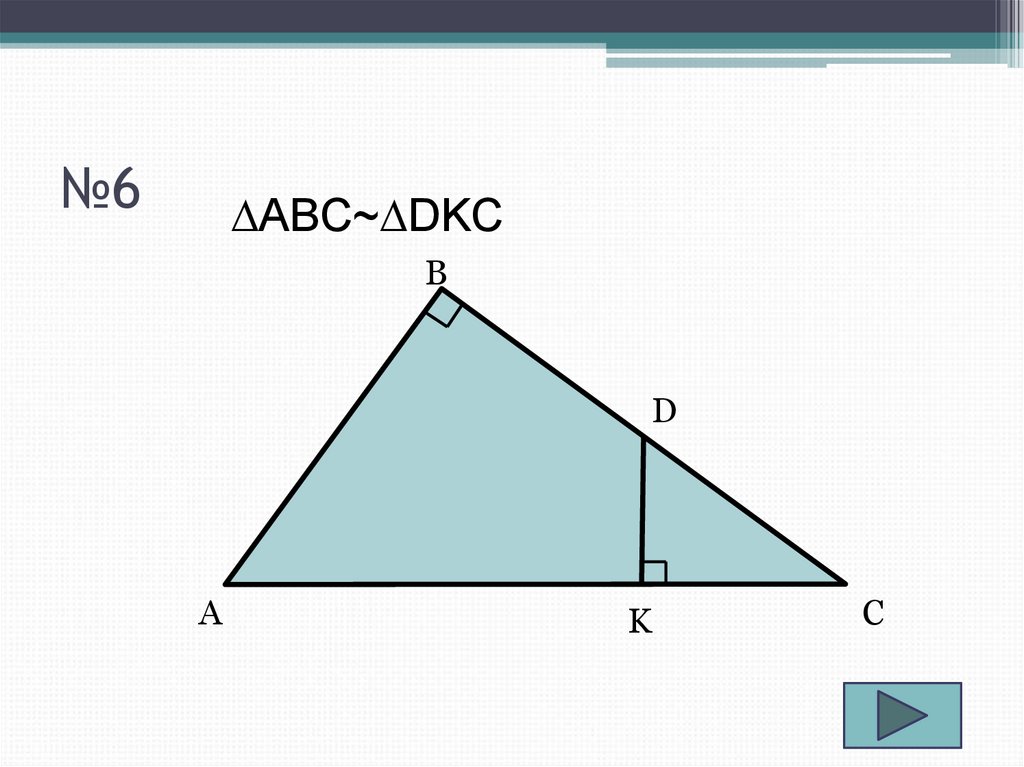
8. №6
∆ABC~∆DKCB
D
A
K
C
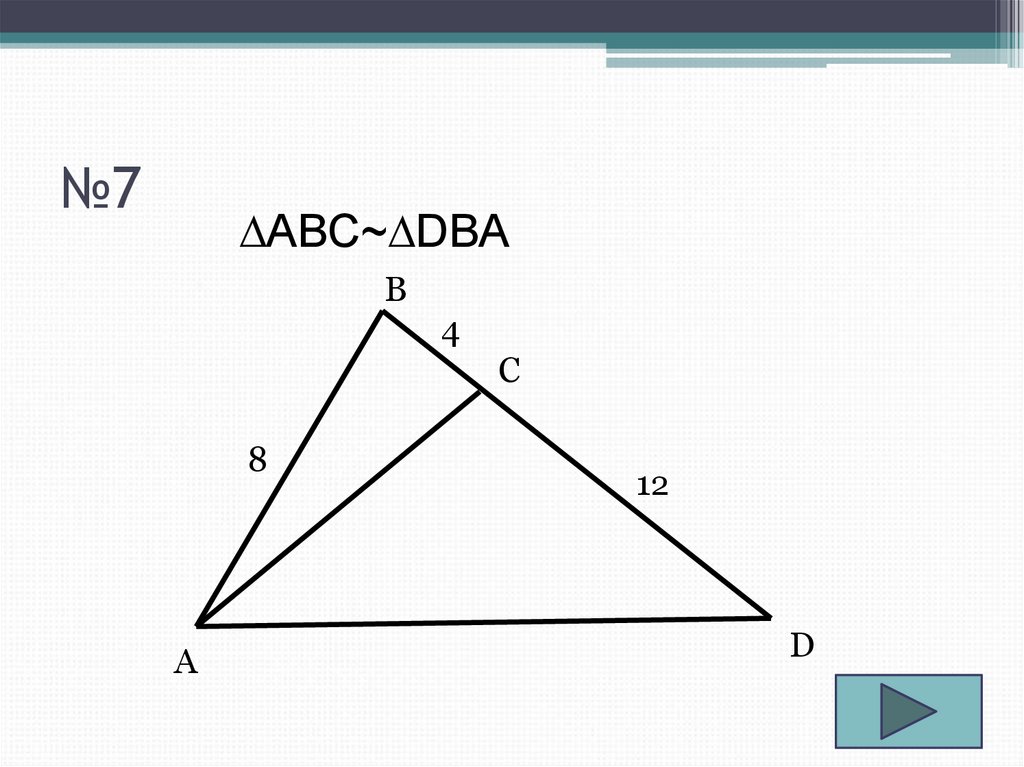
9. №7
∆ABC~∆DBAВ
4
С
8
А
12
D
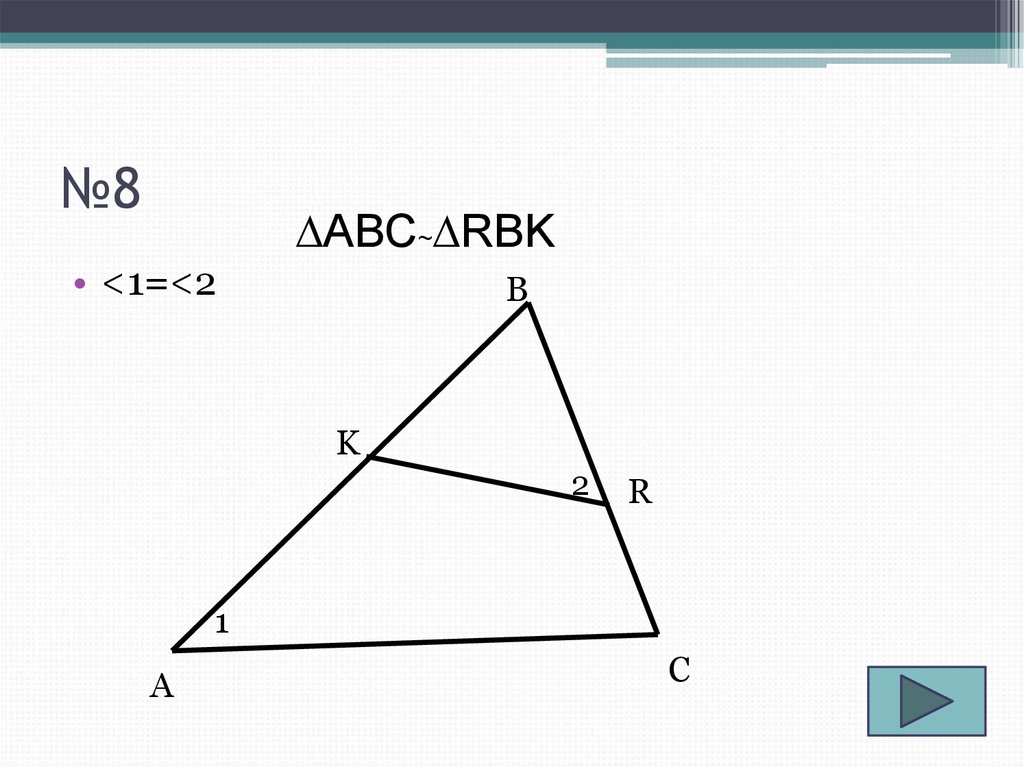
10. №8
∆ABC~∆RBK• <1=<2
B
K
2
R
1
A
C
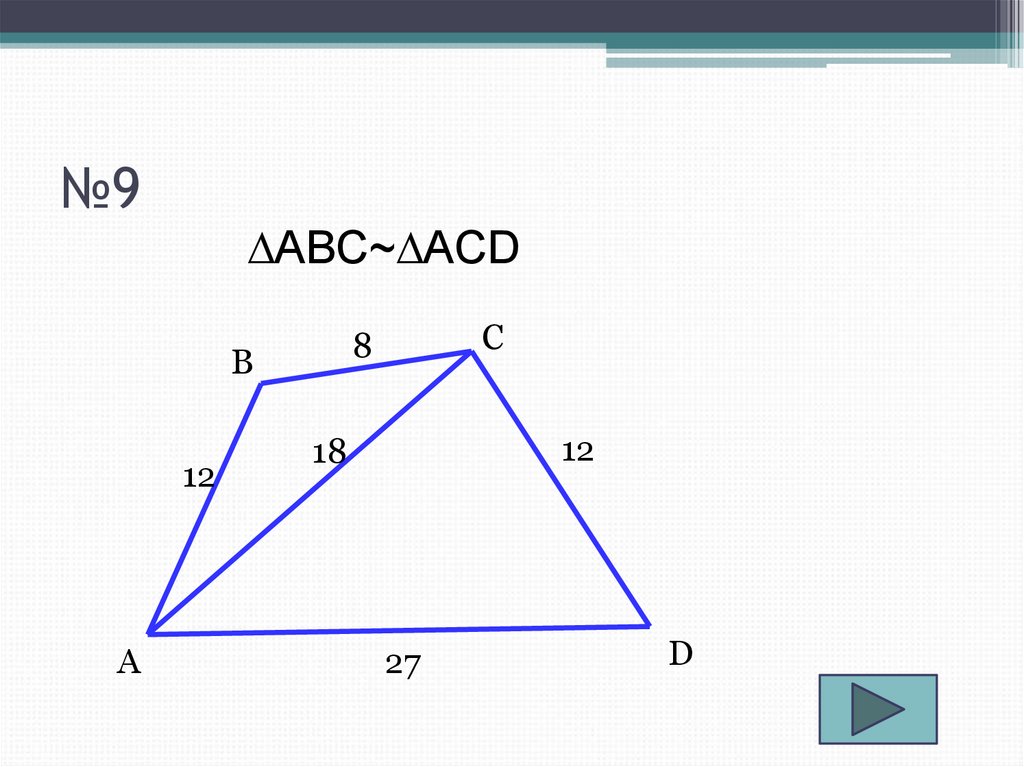
11. №9
∆ABC~∆ACDB
12
A
C
8
12
18
27
D
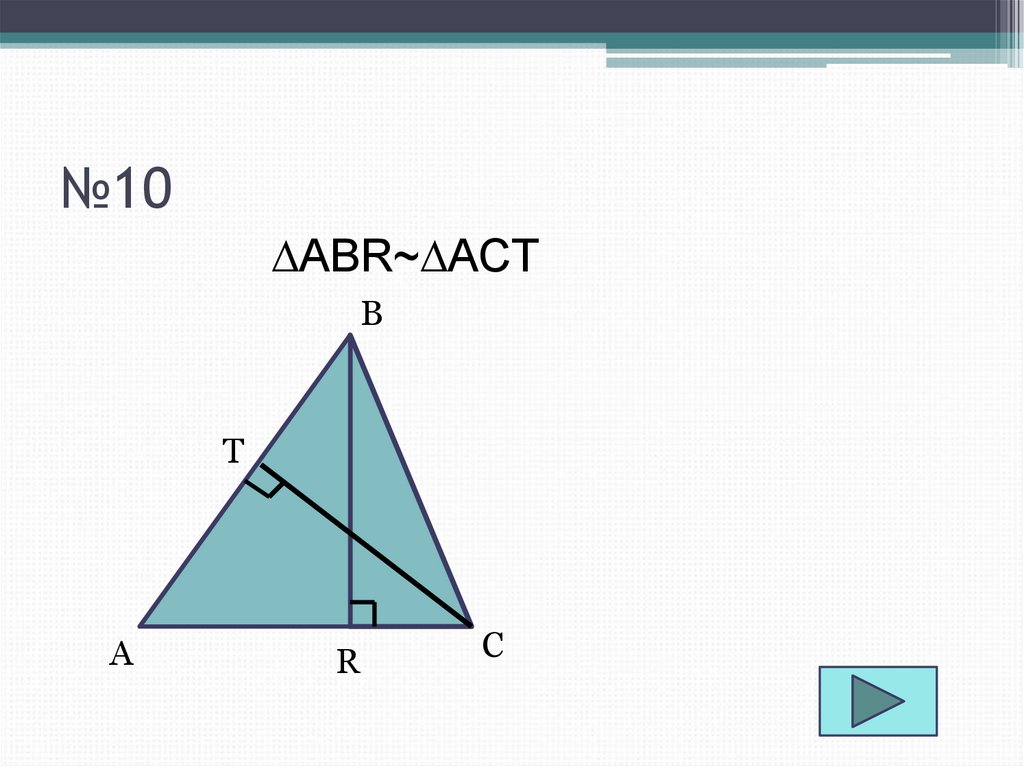
12. №10
∆ABR~∆ACTB
T
A
R
C
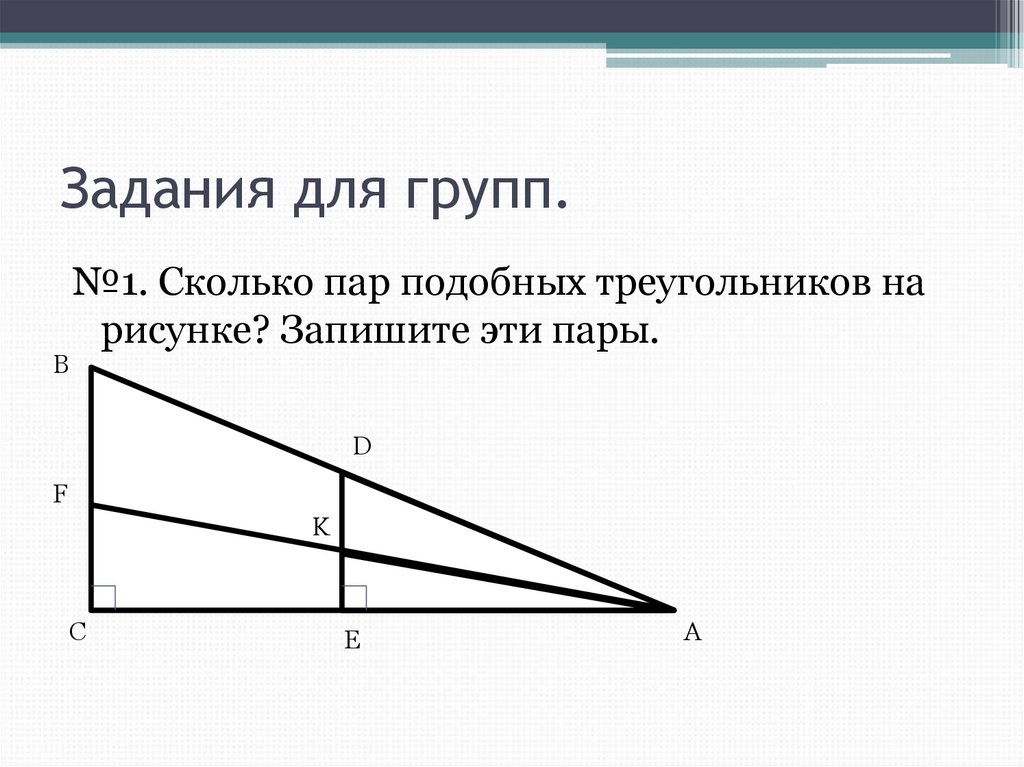
13. Задания для групп.
B№1. Сколько пар подобных треугольников на
рисунке? Запишите эти пары.
D
F
K
С
E
A
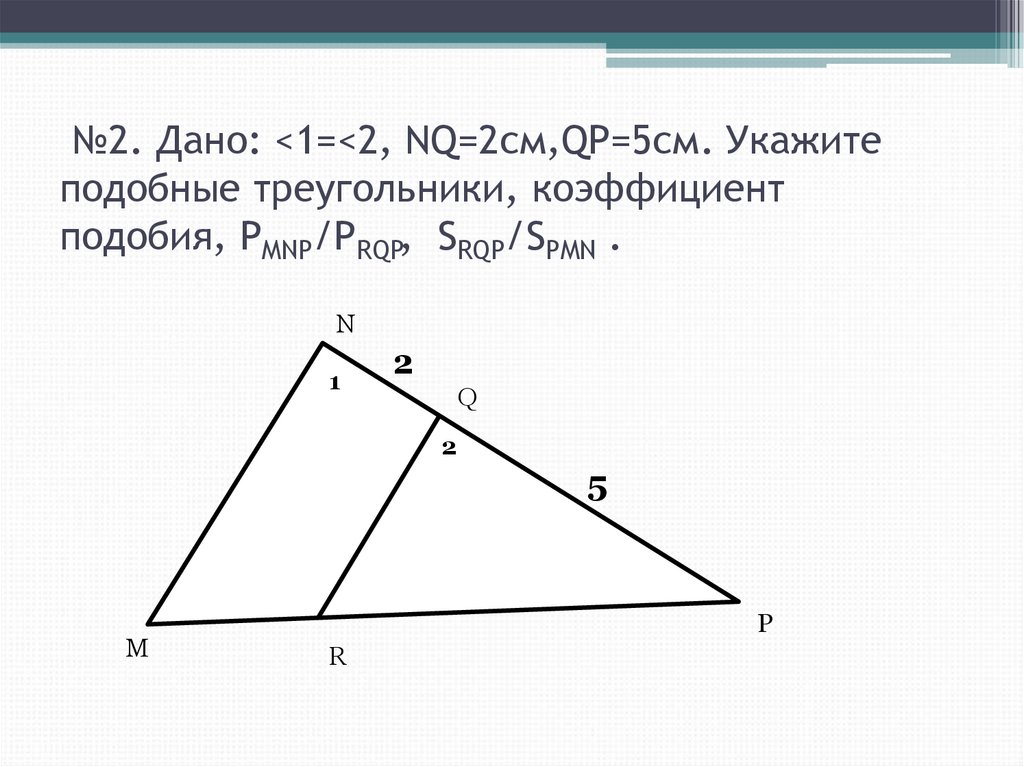
14. №2. Дано: <1=<2, NQ=2см,QP=5см. Укажите подобные треугольники, коэффициент подобия, PMNP/PRQP, SRQP/SPMN .
№2. Дано: <1=<2, NQ=2см,QP=5см. Укажитеподобные треугольники, коэффициент
подобия, PMNP/PRQP, SRQP/SPMN .
N
1
2
Q
2
5
M
P
R
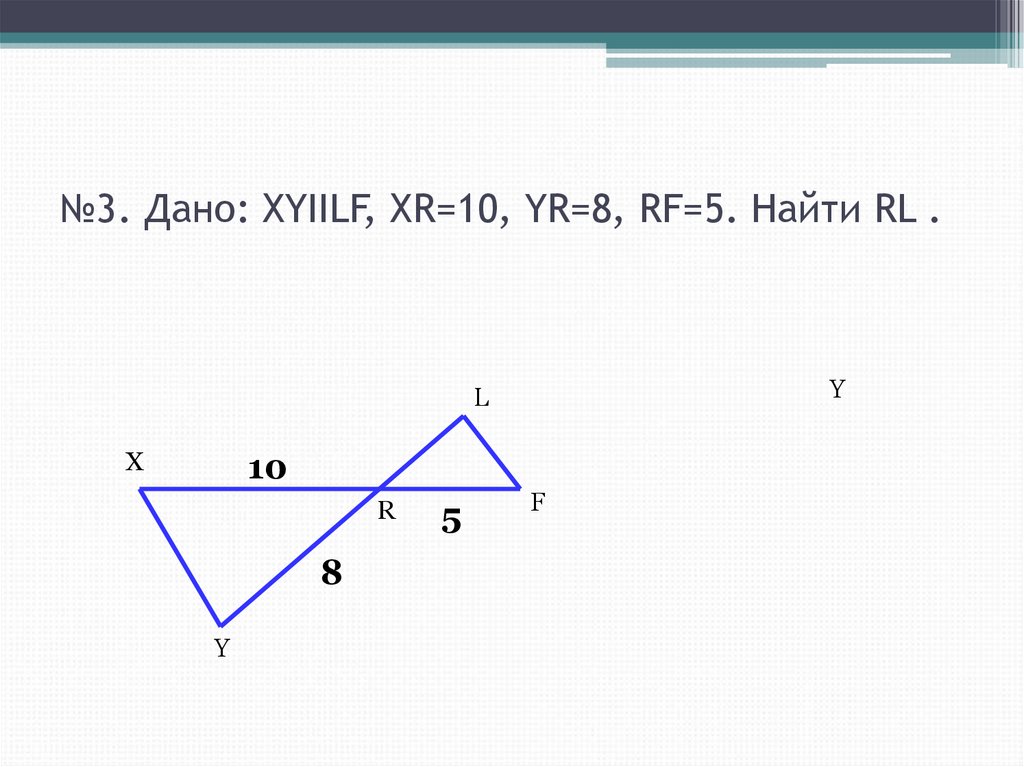
15. №3. Дано: XYIILF, XR=10, YR=8, RF=5. Найти RL .
YL
X
10
R
8
Y
5
F
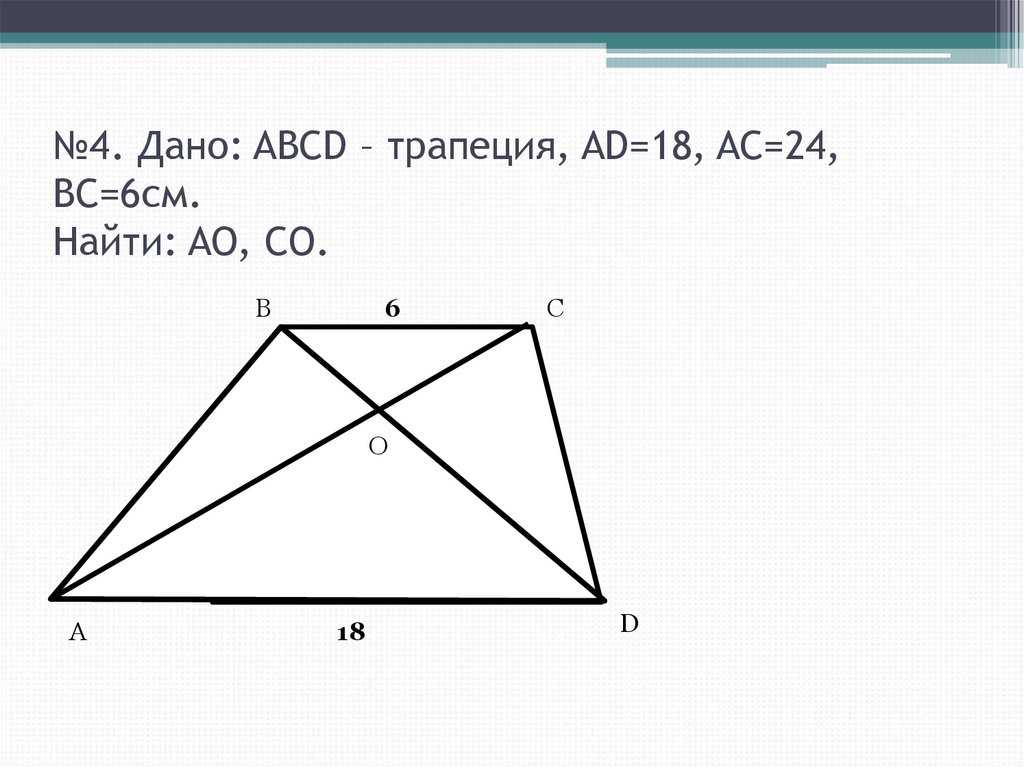
16. №4. Дано: ABCD – трапеция, AD=18, AC=24, BC=6см. Найти: AO, CO.
B6
C
O
A
18
D
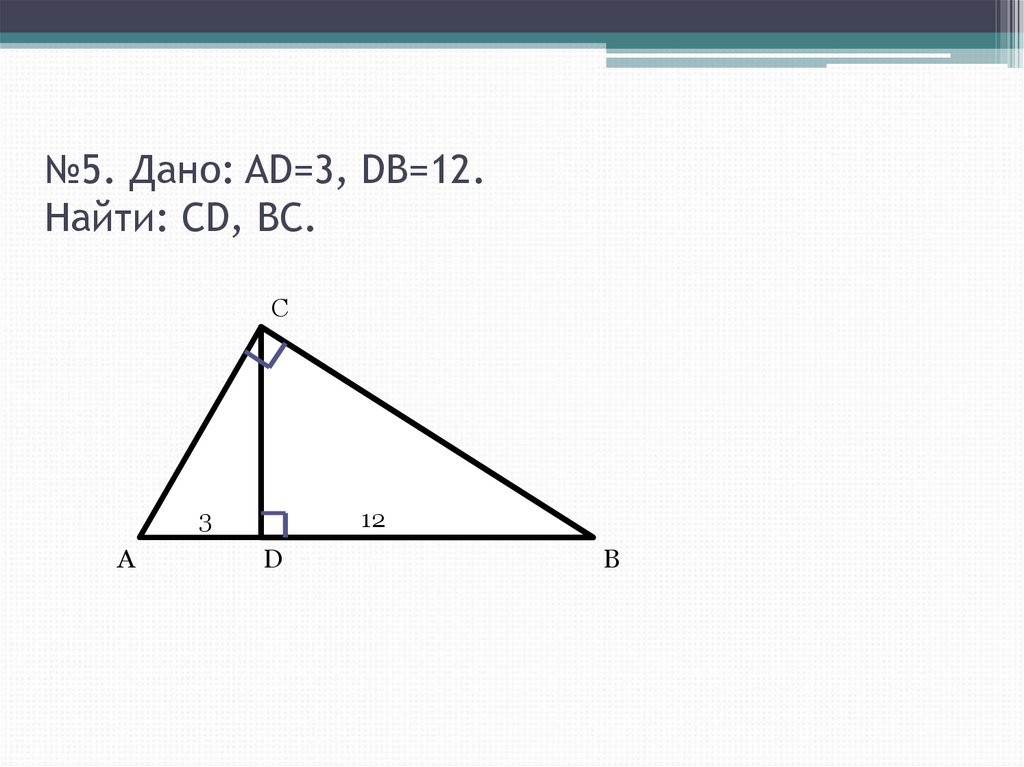
17. №5. Дано: AD=3, DB=12. Найти: CD, BC.
C3
A
12
D
B
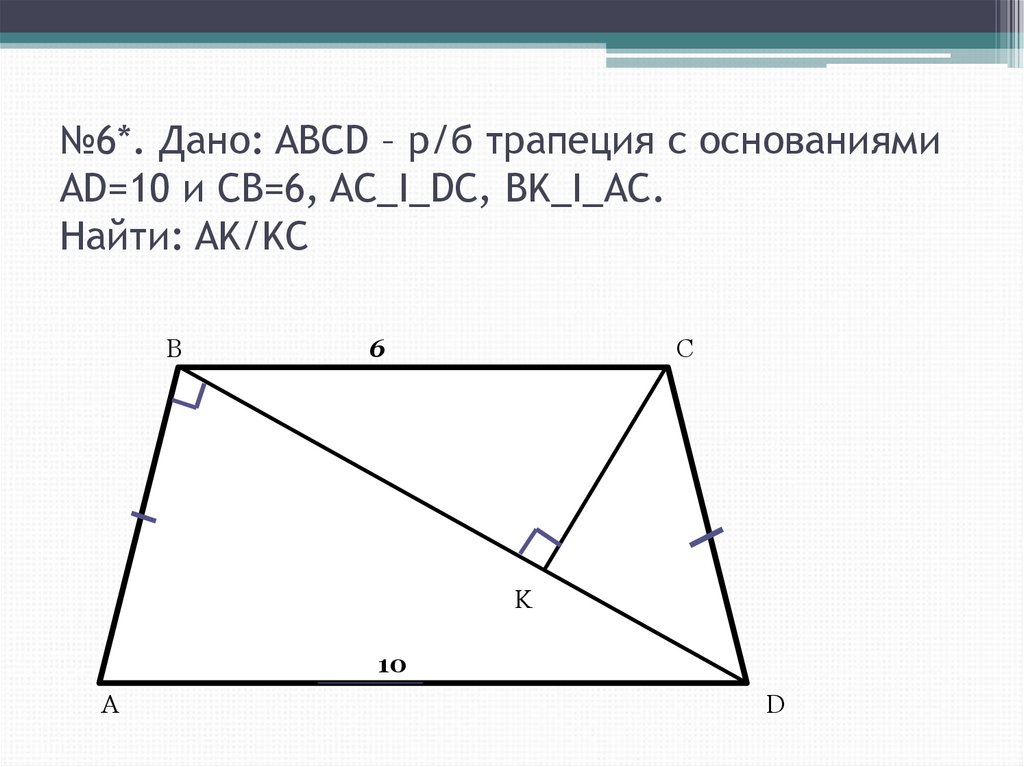
18. №6*. Дано: ABCD – р/б трапеция с основаниями AD=10 и CB=6, AC_I_DC, BK_I_AC. Найти: AK/KC
B6
C
K
10
A
D
19. Ответы к задачам.
• №1. 3 пары: ∆ADE~∆ABC,∆AKE~∆AFC, ∆ADK~∆ABF.
• №2. ∆RQP~∆MNP, PMNP/PRQP=7/5,
SRQP/SMNP=25/49.
• №3. RL=4см.
• №4. Ао=18см,ОС=6см.
• №5. CD=6, BC=6√5.
• №6. AK/CK=2/3.
20.
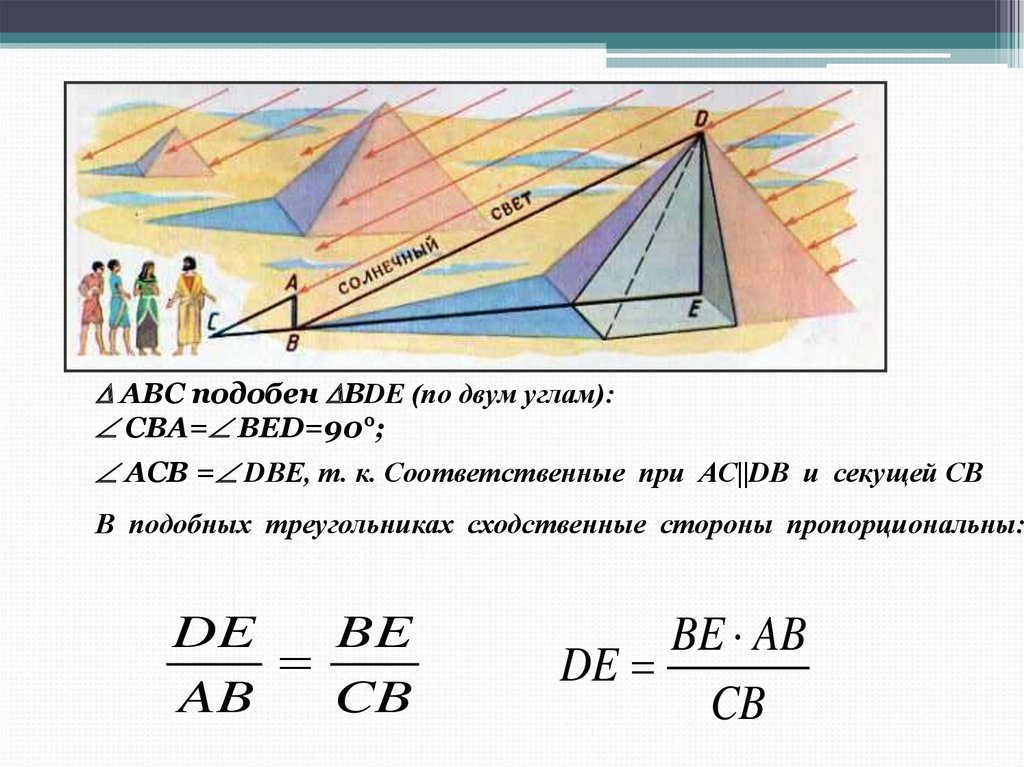
Идея измерения высотыегипетских пирамид с помощью
шеста принадлежит Фалесу.
21.
АВС подобен ВDE (по двум углам):СВА= ВED=90°;
АСВ = DВЕ, т. к. Соответственные при АС||DВ и секущей СВ
В подобных треугольниках сходственные стороны пропорциональны:
DE
BE
AB
CB
BE AB
DE
CB
22.
23.
;;
.
.
АВD ~ EFD (по двум углам):
ВАD= FED=90°;
АDВ = EDF, т.к. угол падения
равен углу отражения.
В подобных треугольниках
сходственные стороны
пропорциональны:
DE FE
AD AB
DE AB
FE
AD












 Математика
Математика








