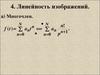Похожие презентации:
Преобразование Лапласа (лекция 7)
1.
Преобразование Лапласа2.
Преобразов анием Лапласа функции f (t )действительной переменной t называется функция
F ( p) комплексно й переменной p i , определяем ая
соотношением
F ( p) f (t )e
pt
dt.
(1)
0
Если интеграл (1) сходится, то функция F ( p)
называется изображением функции f (t ) по Лапласу , а
f (t ) функцией оригиналом или просто оригиналом
функции F ( p). Интеграл в правой части (1) называется
интегралом Лапласа.
3.
Если F ( p) изображение по Лапласу оригинала f (t ),то этот факт записывают в виде
F ( p) f (t ) или F ( p) L{ f (t )},
а если f (t ) оригинал функции F ( p), то
f (t ) F ( p) или
f (t ) L 1{F ( p)}.
4.
В дальнейшем будем всюду полагать, что функцияf (t ) определена для всех значений t и
удовлетворяет следующим условиям
1) f (t ) 0, t 0;
2) При t 0 функция f (t ) на каждом конечном
интервале оси Ot имеет не более чем конечное число
точек разрыва первого рода;
3) f (t ) возрастает не быстрее показательной
функции , то есть существуют такие постоянные
M 0 и 0, что
f (t ) Me t , t 0.
(2)
5.
Точная нижняя грань 0 всех чисел , для которыхсправедливо равенство (2), называется показателе м
роста функции f (t ).
Теорема 1. Всякий оригинал f (t ) имеет изображение
F ( p), являющееся аналитической функцией в
полуплоскости Re p 0 , где 0 показатель роста
f (t ).
Следствие. Если p при
Re p , то
lim F ( p) 0.
6.
Из теоремы 1 следует, что не всякая функция F ( p)может служить изображением некоторого оригинала.
Например , функция F ( p) ctg p имеет бесконечное
множество полюсов pk k , k Z . Поэтому нет такой
области Re p 0 , в которой ctg p является
p
аналитической функцией . Функция F ( p)
также не
p 1
p
является изображением, так как lim
1 0.
p 1
7.
Простейшей функцией оригиналом являетсяединичная функция Хевисайда
1, t 0,
1(t )
0, t 0.
Найдем её изображение. Из
равенства 1(t ) 1 e 0 t
следует, что 1(t ) оригинал с
показателем роста 0 0. По формуле (1) получаем
L{1(t )} e
pt
0
pt
e
1
dt
.
p0
p
1
Следовательно, 1(t ) , где Re p 0.
p
8.
С помощью единичной функции Хевисайда всякийоригинал f (t ) можно представить в виде
f (t ), t 0,
f (t ) 1(t )
0, t 0.
Например , функция sin t определена на всей
действительной оси и не удовлетворяет условию 2)
оригинала. Функция же
sin t , t 0,
sin t 1(t )
0, t 0
есть оригинал. Далее
будут рассматриваться
только оригиналы и 1(t )
будем опускать.
9.
Пример. Найти изображение оригиналова ) f (t ) e at ,
б ) f (t ) t.
а ) Согласно формуле (1) имеем
0
0
L{e at } e at e pt dt e ( p a ) t dt
( p a ) t
1
e
1
( p a )t
e
d [ ( p a )t ]
,
( p a) 0
( p a) 0
p a
если Re p a. Поэтому
1
e
.
p a
at
10.
б ) Применяя (1), получаемdv e pt dt ,
e pt
L{t} te pt dt
du dt , v
0
p
u t,
pt
te
p
0
1
1 pt
1
pt
e dt 2 e
2 , Re p 0,
p 0
p
p
0
t
1
так как lim te lim pt lim
0. Следовательно,
pt
t
t e
t pe
1
t 2 .
p
Используя метод математической индукции , можно
n!
n
доказатиь, что t n 1 , где Re p 0.
p
pt
11.
Свойствапреобразования
Лапласа
12.
1) Линейность . Если f1 (t ) и f 2 (t ) оригиналы споказателями роста 1 и 2 соответственно, то
линейная комбинация 1 f1 (t ) 2 f 2 (t ), 1 , 2 C
является оригиналом с показателем роста
max{ 1 , 2 }, и
L{ 1 f1 (t ) 2 f 2 (t )} 1L{ f1 (t )} 2 L{ f 2 (t )}.
13.
2) Теорема 2 (подобия или масштаба). Еслиf (t ) F ( p ) и любое положительное число, то
1 p
f ( t )
F .
3) Теорема 3 (смещения ). Если f (t ) F ( p ), то
для любого C
e t f (t ) F ( p ).
14.
4) Смещение в области оригинала. Пусть f (t )оригинал. Тогда f (t a), a 0, так же является
оригиналом с аргументом, запаздывающим на величину a.
Теорема 4 ( запаздывания ). Если f (t ) F ( p) и a
любое положительное число, то
f (t a) e pa F ( p).
Теорема 4' (опережения ). Если
f (t ) F ( p) и a любое
положительное число, то
a
pa
pt
f (t a) e F ( p) f (t )e dt .
0
15.
5) Теорема 5 (дифференци рования оригинала ).Если f (t ), f (t ), , f ( n ) (t ) оригиналы и f (t ) F ( p), то
f ( n ) (t ) p n F ( p) [ p n 1 f (0) p n 2 f (0) f ( n 1) (0)].
6) Теорема 6 (дифференци рования изображени я ).
Если f (t ) F ( p), то
F ( n ) ( p) ( t ) n f (t ).
16.
7) Теорема 7 (интегрирования оригинала ).Если f (t ) F ( p ), то
t
F ( p)
0 f ( )d p .
8) Теорема 8 (интегрирования изображени я ).
Если f (t ) F ( p ) и интеграл F ( s )ds сходится, то
p
f (t )
F ( s ) ds.
t
p
17.
9) Изображение свёртки оригиналов.Свёрткой двух оригиналов f1 (t ) и f 2 (t ) называется
функция , обозначаемая f1 (t ) f 2 (t ) и определяемая
равенством
f1 (t ) f 2 (t ) f1 ( ) f 2 (t )d .
Поскольку f1 ( ) 0 при 0 и f 2 (t ) 0 при t ,
то для свёртки получаем следующее выражение :
t
f1 (t ) f 2 (t ) f1 ( ) f 2 (t )d .
0
Можно доказать, что свёртка двух оригиналов есть
оригинал.
18.
Свёртка обладает основными свойствами операцииумножения :
а) f1 f 2 f 2 f1 (коммутативность),
б ) f1 f 2 f 3 f1 f 2 f 3 (ассоциативность),
в ) 1 f1 2 f 2 f 3 1 f1 f 3 2 f 2 f 3
( линейность).
Теорема 9 ( Бореля ). Если f1 (t ) F1 ( p) и
f 2 (t ) F2 ( p), то произведение F1 ( p) F2 ( p) является
изображением свёртки оригиналов f1 (t ) и f 2 (t ), то
есть
t
F1 ( p) F2 ( p) f1 ( ) f 2 (t )d f1 (t ) f 2 (t ).
0
19.
10) Интеграл Дюамеля . Если Если f1 (t ) F1 ( p ) иf 2 (t ) F2 ( p ), то
t
pF1 ( p ) F2 ( p ) f1 (t ) f 2 (0) f1 ( ) f 2 (t )d
(3)
0
или
t
pF1 ( p ) F2 ( p ) f1 (0) f 2 (t ) f1 (t ) f 2 ( )d . (4)
0
Равенство (3) или (4) называется формулой
Дюамеля.
20.
Определение оригиналапо его изображению
21.
Элементарн ый метод. Во многих случаяхзаданное изображение можно преобразовать к
такому виду, когда оригинал легко восстанавливается
непосредственно с помощью свойств преобразования
Лапласа и таблицы изображений.
Для преобразования изображения широко
используется в этом случае метод разложения
рациональной дроби в сумму простейших.
22.
Пример. Найти оригинал по его изображению3 p2 p 1
F ( p)
.
( p 1)( p 2) p
Разложим F ( p) на простейшие дроби :
3 p2 p 1
A
B
C
F ( p)
( p 1)( p 2) p p 1 p 2 p
A( p 2) p B( p 1) p C ( p 1)( p 2)
( p 1)( p 2) p
3 p 2 p 1 A( p 2) p B( p 1) p C ( p 1)( p 2)
3 p 2 p 1 Ap 2 2 Ap Bp 2 Bp Cp 2 Cp 2C
23.
3 p 2 p 1 ( A B C ) p 2 (2 A B C ) p 2Cp2
p1
p0
A B C 3,
2 A B C 1,
2C 1,
A 1,
B 3 2 ,
C 1 2 ,
или в равенство
3 p 2 p 1 A( p 2) p B( p 1) p C ( p 1)( p 2)
последовательно подставляем p 1, p 2 и p 0 :
p 1 3 A 3 0 0 A 1,
p 2 9 0 B 6 0 B 3 2 ,
p 0 1 0 0 C ( 2) C 1 2 .
24.
Тогда,A
B
C
1
3
1
F ( p)
.
p 1 p 2 p p 1 2( p 2) 2 p
Учитывая, что
1
1
1
t
2t
e ,
e ,
1
p 1
p 2
p
и свойство линейности, получаем
3 2t 1
t
f (t ) e e .
2
2
25.
Теорема 1. Если функция f (t ) является оригиналом,а F ( p ) ее изображением, то в любой точке t , где
оригинал f (t ) непрерывен,
i
1
pt
f (t )
F
(
p
)
e
dp,
2 i i
(1)
причем интегрирование производится вдоль любой
прямой Re p 0 , 0 показатель роста функции
f (t ) и интеграл понимается в смысле главного значения,
то есть
i
pt
F
(
p
)
e
dp lim
i
b
i b
pt
F
(
p
)
e
dp.
i b
26.
Формула (1) определяет обратное преобразованиеЛапласа , позволяюще е восстановить оригинал f (t ) по
соответствующему ему изображению F ( p). Эта
формула называется также формулой Меллина .
Замечание. Во всякой точке t0 , являющейся точкой
разрыва функции f (t ), правая часть формулы (1) равна
f (t0 0) f (t0 0)
.
2
Непосредственно применение формулы (1) часто
затруднительно, и обычно пользуются теоремами
разложения , являющимис я следствиями из нее.
27.
Теорема 2 (первая теорема разложения ) . ЕслиF ( p ) аналитическая функция в окрестности точки
p и ряд Лорана F ( p) с центром в этой точке
имеет вид
cn c1 c2
cn
F ( p) n 2 n ,
p p
p
n 1 p
то оригиналом f (t ) функции F ( p) является
cn
c3 2
cn 1 n
c2
n 1
f (t )
t c1 t t
t ,
1!
2!
n!
n 1 ( n 1)!
причем этот ряд сходится при всех t.
28.
Пример. Найти оригинал по его изображениюp4
F ( p) 5 .
p 1
Особыми точками функции F ( p) являются корни
уравнения p 5 1 0. Эти точки лежат на окружности
p 1. Значит, в области p 1, которая является
окрестностью бесконечно удаленной точки, функцию
F ( p) можно представить рядом Лорана по степеням p,
то есть в виде
p4
5
p 1
p4
1
1
1 1
1
1
6 11 5 n 4
p p
p
p
1 p 1 1
5
p 1 5
5
p
p
29.
То есть1 1
1
1
F ( p) 6 11 5 n 4
p p
p
p
Применяя к F ( p) теорему 2, получаем
t 5 t 10
t 5 n 5
f (t ) 1
5! 10!
(5n 5)!
30.
Теорема 3 (вторая теорема разложения ) . Еслиизображение F ( p) является однозначной функцией и
имеет лишь конечное число особых точек p1 , p2 , , pn ,
лежащих в конечной части полуплоскости Re p 0 ,
то
n
f (t ) Res F ( p)e pt .
k 1
p pk
(2)
31.
Пример. Найти оригинал по его изображению1
F ( p) 2 2
.
p ( p 1)
Функция F ( p ) удовлетворяет условиям теоремы 3.
Изолированными особыми точками этой функции являются
p 0 (полюс второго порядка ), p i и p i (простые
полюсы). Найдем вычеты функции F ( p)e pt в полюсах
функции F ( p ) :
Res F ( p )e
p 0
pt
2
1
pt
lim p 2 2
e
p 0
p ( p 1)
p
e pt
te pt ( p 2 1) e pt 2 p
lim 2 lim
t,
2
2
p 0 p 1
p 0
( p 1)
p
32.
ptpt
1
pt
Res F ( p)e lim ( p i ) 2 2
e
p
i
p i
p ( p 1)
( p i )e pt
e pt
eit
lim 2
lim 2
,
p i p ( p i )( p i )
p i p ( p i )
2i
1
pt
Res F ( p)e lim ( p i ) 2 2
e
p
i
p i
p ( p 1)
( p i )e pt
e pt
e it
lim 2
lim 2
.
p i p ( p i )( p i )
p i p ( p i )
2i
По формуле (2) получаем
eit e it
eit e it
f (t ) t
t
t sin t.
2i 2i
2i
33.
Таблица оригиналов и их изображени й для функций,часто встречающи хся при решении задач
№
1
f (t )
F ( p)
№
f (t )
F ( p)
1(t )
1
p
7
ch t
p
p 2 2
2
e
t
1
p
8
t
e sin t
( p ) 2 2
3
tn
n!
p n 1
9
t
p
( p ) 2 2
4
sin t
p 2 2
10
e sh t
( p ) 2 2
5
cos t
p
p 2 2
11
e t ch t
p
( p ) 2 2
6
sh t
p 2 2
12
t n
e cos t
t
e t
n!
( p ) n 1






















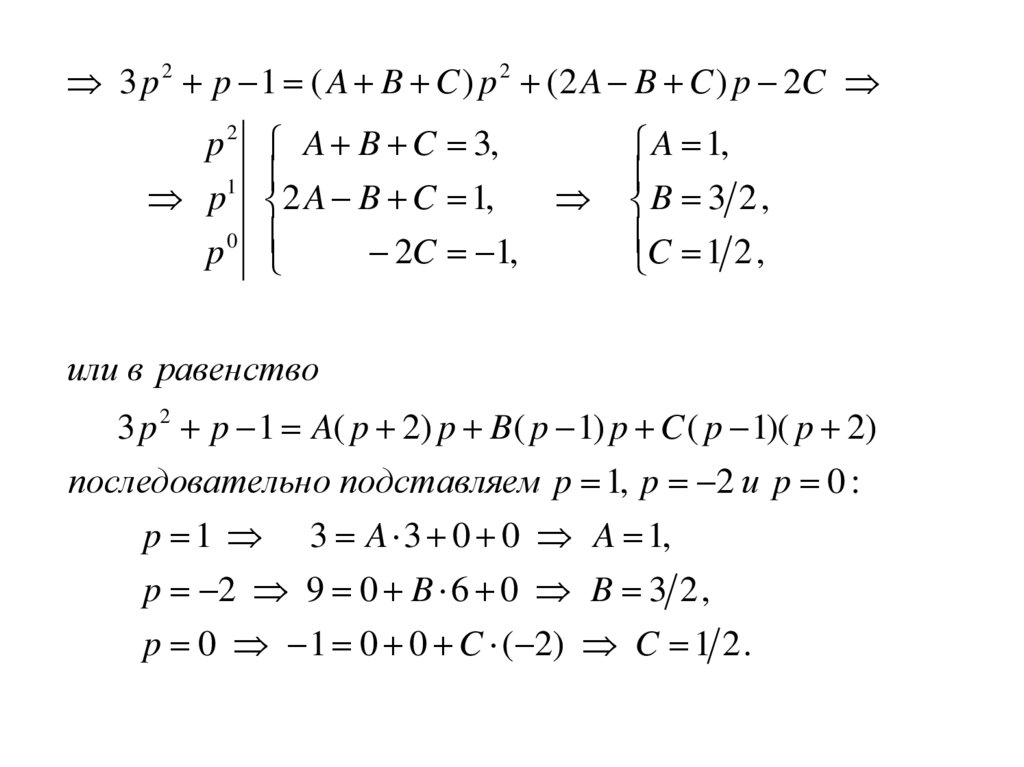










 Математика
Математика