Похожие презентации:
Неопределенный интеграл. Математический анализ. 1 курс, 2-й семестр
1.
Математическийанализ
1 курс, 2-й семестр
2.
1. Неопределенный интеграл2
3.
Первообразная• Функция F(x) называется первообразной функции f(x), если
функция F(x) дифференцируема и F’(x) = f(x).
• Например, если f(x) = 2x, то ее первообразной будет являться
функция x2.
• Но это не единственная первообразная. Например, x2 + 1 также
будет первообразной для 2x.
3
4.
Первообразная• Утверждение: Если F1(x) и F2(x) – две первообразные функции f(x),
то их разность F1(x) – F2(x) постоянное число.
• Таким образом, если F(x) – первообразная функции f(x), то все
остальные первообразные этой функции можно представить в
виде F(x) + C, где C – любая константа.
• Множество всех первообразных функции f(x) называется
неопределенным интегралом и обозначается ∫f(x)dx.
• Если F(x) – некоторая первообразная функции f(x), то ∫f(x)dx = F(x)
+ C, где C – неопределенная константа.
4
5.
Таблица интегралов• Из таблицы производных легко получить таблицу интегралов
элементарных функций.
n 1
x
1. x n dx
C (n 1),
n 1
1
2. dx ln x C,
x
x
a
x
3. a dx
C,
ln a
4. e dx e C,
x
x
5. sinxdx cosx C,
6. cosxdx sinx C,
1
7.
dx tg x C,
2
cos x
1
8. 2 dx ctgx C,
sin x
5
6.
Таблица интеграловarcsinx C,
dx
9.
2
1 x
arccosx C,
arctgx C,
1
dx
10.
2
1 x
arcctgx C,
1
11.
1
dx ln x x2 1 C,
x2 1
1 1 x
1
C.
dx ln
12.
2
2 1 x
1 x
6
7.
Свойства интеграла1. (∫f(x)dx)’ = f(x).
∫(f(x)+g(x))dx = ∫f(x)dx + ∫g(x)dx.
3. ∫αf(x)dx = α∫f(x)dx.
2.
По формуле производной сложной функции (f(kx + b))’ = f’(kx +
b) · (kx + b)’ = k · f’(kx + b).
4. Пусть F(x) – первообразная функции f(x). Тогда
∫f(kx + b)dx = F(kx + b)/k + C.
7
8.
Пример• Вычислить ∫(2x + 3)4 dx.
5
x
4
C.
• Согласно таблице интегралов: xdx
5
• Значит:
5
(2x
3)
4
(2x
3)
dx
C.
10
8
9.
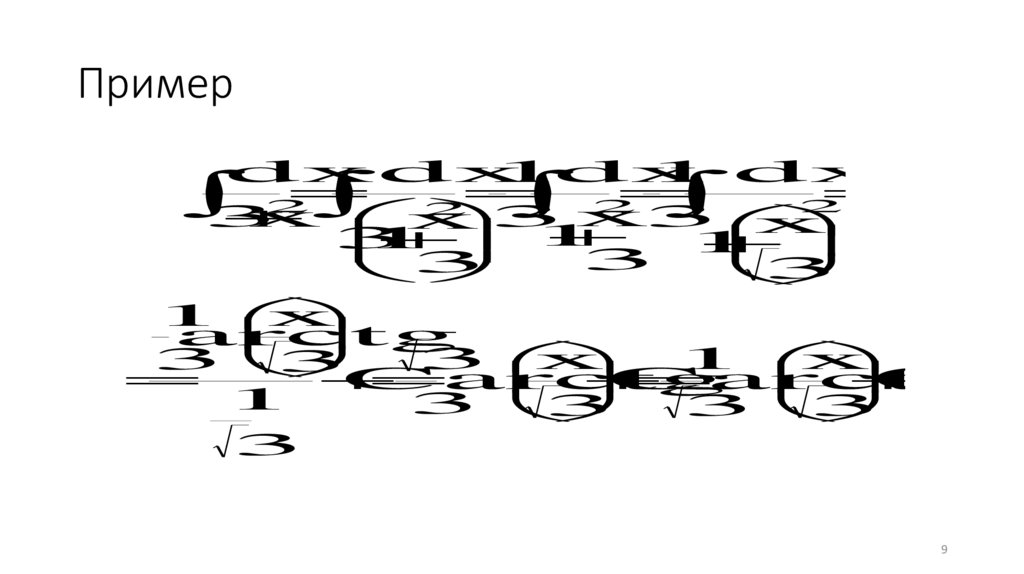
Примерdx dx
1dx
1 dx
2
2
2
2
3
x x
3 x3
x
1
3
1
1
3
3
3
1
x
arctg
3
x
1
x
3
3
C
arctg
C
arctg
C.
1
3
3
3
3
3
9
10.
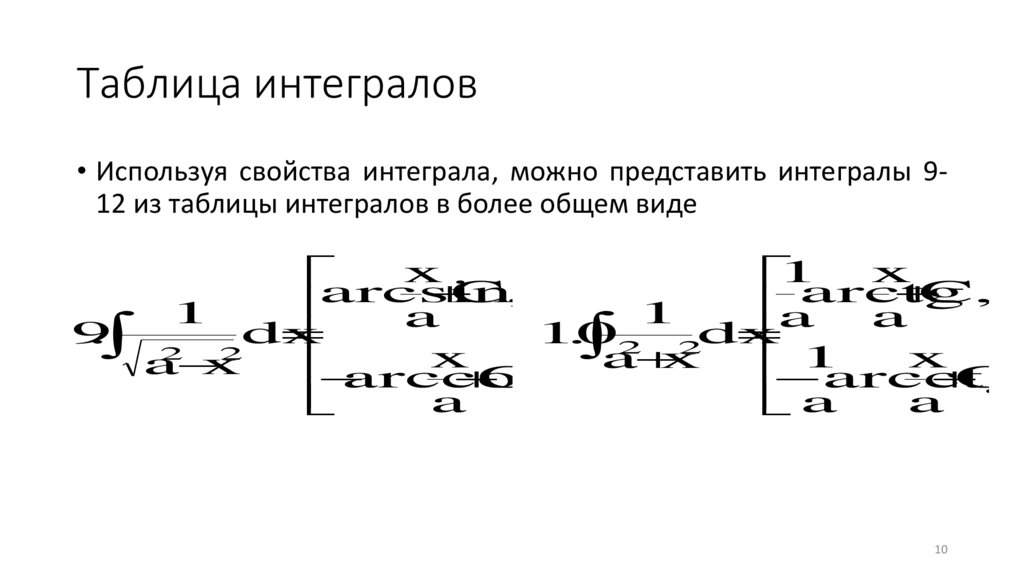
Таблица интегралов• Используя свойства интеграла, можно представить интегралы 912 из таблицы интегралов в более общем виде
x
1
x
arcsin
C,
arctg
C,
1
1
a
a
a
9
.
dx
10
. 2 2dx
2
2
x
1
x
a
x
a
x
arccos
C,
arcctg
C,
a
a
a
10
11.
Таблица интегралов11
.
1
dx
lnx x A C
,
x2 A
1
1 a x
12
. 2 2 dx
ln
C,
a x
2a a x
2
1
1 x a
13
. 2 2 dx
ln
C
x a
2a x a
11
12.
Интегрирование по частям• Пусть u = u(x), v = v(x) – некоторые функции.
• Из формулы производной произведения (uv)’ = u’v + v’u следует,
что ∫(uv)’dx = ∫u’vdx + ∫v’udx.
• Из свойств интеграла ∫(uv)’dx = uv.
• Из свойств дифференциала u’dx = du, v’dx = dv.
• Отсюда uv = ∫vdu + ∫udv. Преобразуя, получаем формулу
интегрирования по частям:
∫udv = uv – ∫vdu.
12
13.
Интегрирование по частям• Использовать этот метод стоит в том случае, если вычисление
интеграла ∫vdu проще, чем вычисление интеграла ∫udv.
• Первый тип функций, которые удобно интегрировать по частям:
P(x) ex, P(x) sin x, P(x) cos x, где P(x) – произвольный многочлен.
• При интегрировании функций данного типа за u следует взять
многочлен P(x).
13
14.
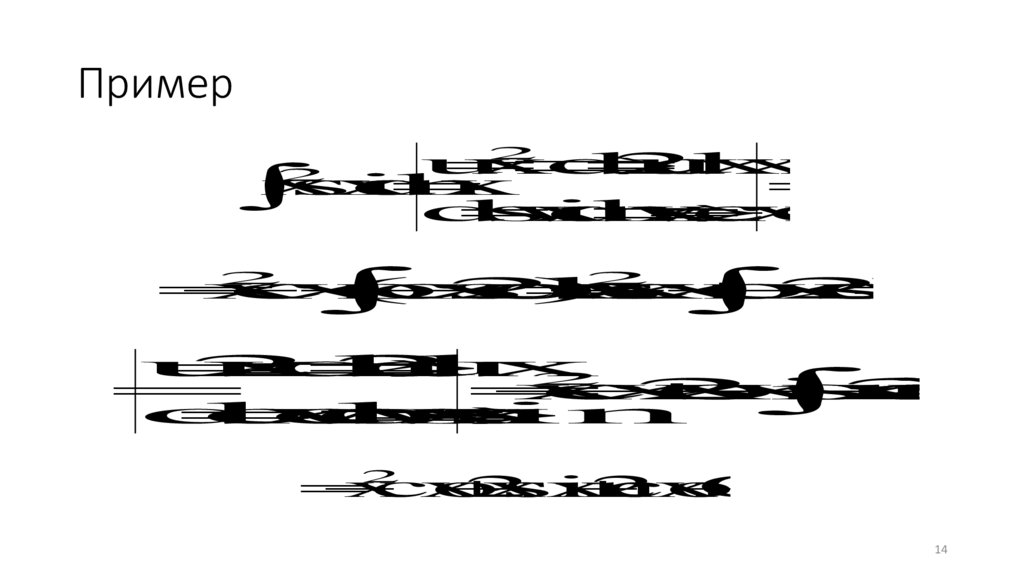
Примерu
x
du
2x
dx
x
sin
x
dx
dv
sin
x
dx
v
cos
x
2
2
x
cos
x
(
cos
x)
2x
dx
x
cos
x
cos
x
2x
dx
2
2
u
2
x
du
2
dx
2
x
cos
x
2
x
sin
x
sin
x
2
dx
dv
cos
x
dx
v
sin
x
2
x
cos
x
2
x
sin
x
2
cos
x
C.
14
15.
Интегрирование по частям• Второй тип функций, которые удобно интегрировать по частям:
P(x) ln x, P(x) arcsin x, P(x) arccos x, P(x) arctg x, P(x) arcctg x, где P(x)
– произвольный многочлен.
• При интегрировании функций данного типа за u следует взять
ln x, arcsin x, arccos x, arctg x или arcctg x.
15
16.
Примерdx
u
ln
x
du
3
3
x
x
dx
x
2
x
ln
x
dx
ln
x
3
3 3
x
x
2
dv
x
dx
v
3
3
2
3 3
xx
xx
ln
x
dx
ln
x
C
33
39
16
17.
Интегрирование по частям• Третий тип функций, которые удобно интегрировать по частям:
ex sin x, ex cos x.
• Это так называемые циклические интегралы.
17
18.
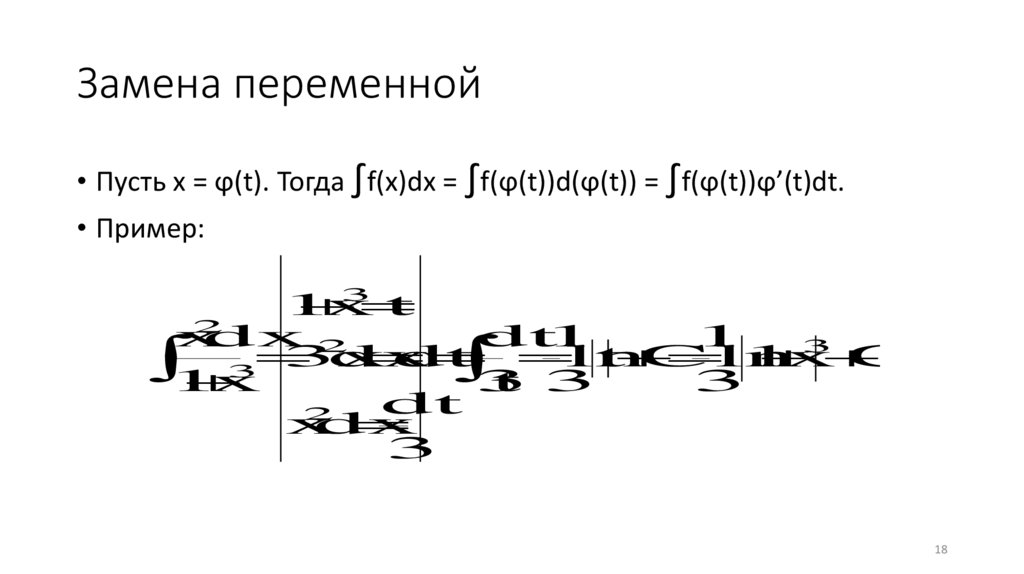
Замена переменной• Пусть x = ϕ(t). Тогда ∫f(x)dx = ∫f(ϕ(t))d(ϕ(t)) = ∫f(ϕ(t))ϕ’(t)dt.
• Пример:
1
x
t
2
x
dx 2
dt1
1
3
3x
dx
dt
ln
t
C
ln
1
x
C.
3
1
x
3
t 3
3
dt
2
x
dx
3
3
18
19.
Интегрирование рациональных функций20.
Интегрирование рациональных функцийСначала научимся интегрировать так называемые простейшие
дроби. Это
21.
Интегрирование рациональных функцийДроби I и II интегрируются легко.
Для дробей III и IV конструкция следующая.
Выделяем полный квадрат.
22.
Интегрирование рациональных функцийТеперь в случае III имеем
23.
Интегрирование рациональных функцийВ случае IV, используя ту же подстановку
имеем
24.
Интегрирование рациональных функцийДля нахождения второго интеграла в правой части можно
использовать следующую рекуррентную формулу.
25.
Интегрирование рациональных функций(разложение правильных дробей на простые)
26.
Интегрирование рациональных функций(разложение правильных дробей на простые)
Каждому сомножителю из разложения (*) сопоставляем сумму
простых дробей:
27.
Интегрирование рациональных функций(разложение правильных дробей на простые)
Пример
28.
Интегрирование рациональных функций(разложение правильных дробей на простые)
Пример
29.
Интегрирование иррациональных функций• Если подынтегральная функция содержит выражение вида
n
то, полагая
ax b
,
cx d
ax b
t
,
cx d
n
получим
dtn b
x
.
n
a ct
29
30.
Подстановки Эйлера30
31.
Условия Чебышева• Пусть n, m и p – рациональные числа. Интеграл вида
m
np
x
(a
bx
) dx
выражается через конечную комбинацию элементарных функций
только в следующих случаях:
1)p – целое число;
2)(m + 1)/n – целое число;
3)(m + 1)/n + p – целое число.
31
32.
Условия Чебышева• В первом случае следует сделать замену x = ts, где s –
наименьший общий знаменатель чисел n и m.
• Во втором случае следует сделать замену a + bxn = ts, где s –
знаменатель числа p.
• В третьем случае следует сделать замену ax-n + b = ts, где s –
знаменатель числа p.
32
33.
Тригонометрические подстановки• В подынтегральной функции иррационального вида можно
избавиться от иррациональности, используя следующие замены:
x asin
t a2 x2 acos
t;
x acos
t a2 x2 asin
t;
x asec
t x2 a2 atgt;
x atgt x2 a2 asec
t.
33
34.
Тригонометрические интегралы• Если в подынтегральной функции встречается sinnxdx или cosnxdx,
где n – нечетная степень, то можно представить их в виде
sinn-1x·sinxdx или cosn-1x·cosxdx и сделать замену t = сosx или t =
sinx соответственно.
• Если в подынтегральной функции встречается sinnxdx или cosnxdx,
где n – четная степень, то можно воспользоваться формулами
понижения степени:
1
cos2x
cos2x
2 1
cos
x
;sin
x
.
2
2
2
34
35.
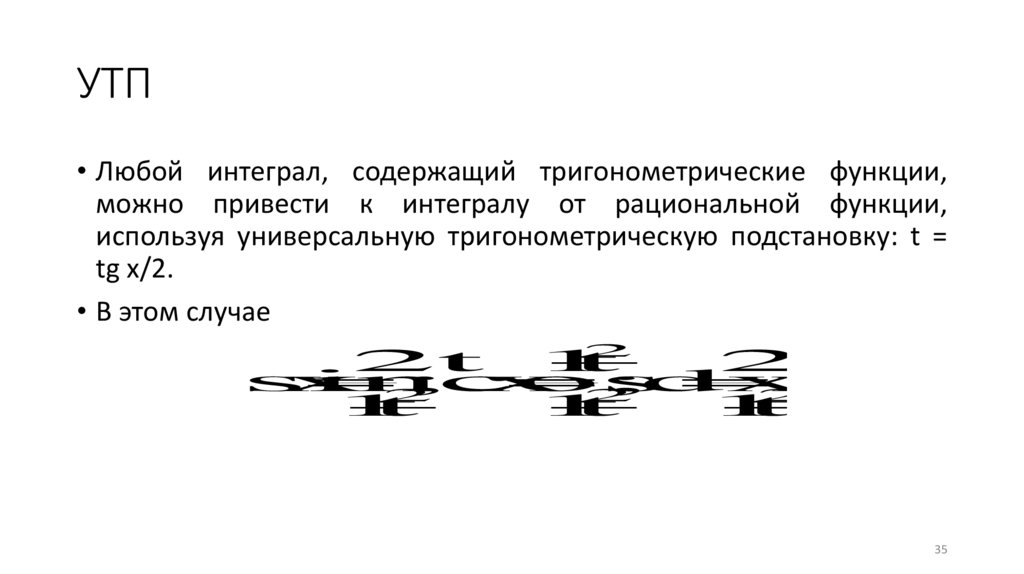
УТП• Любой интеграл, содержащий тригонометрические функции,
можно привести к интегралу от рациональной функции,
используя универсальную тригонометрическую подстановку: t =
tg x/2.
• В этом случае
2t 1
t
2dt
sin
x
;cos
x
;dx
.
2
2
2
1
t
1
t
1
t
2
35







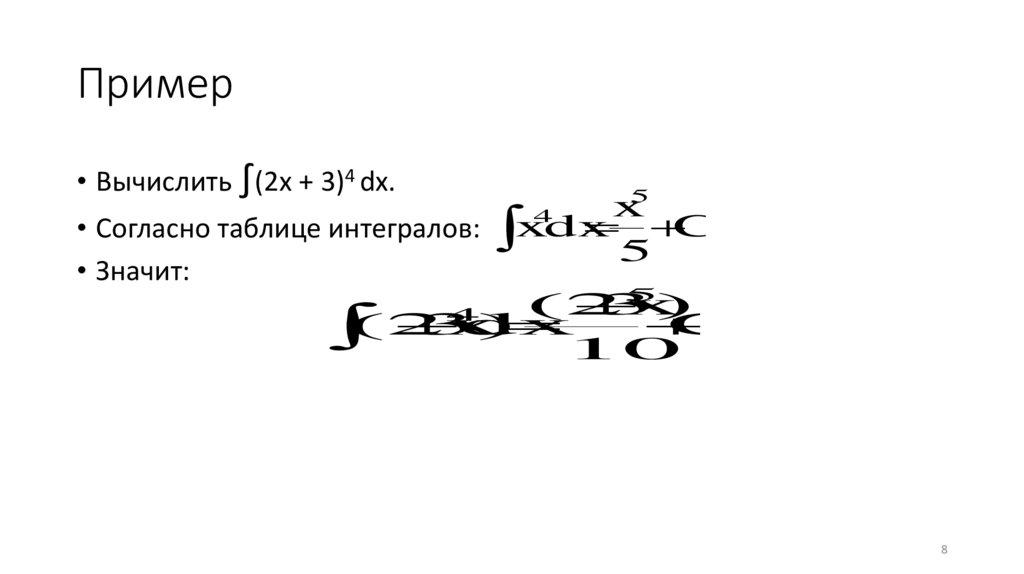




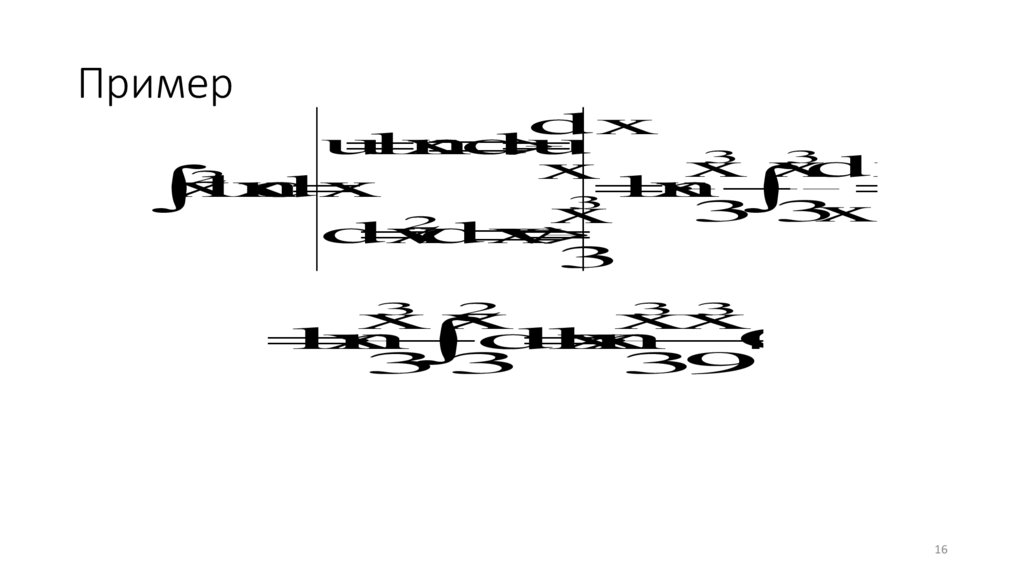

















 Математика
Математика








