Построение графиков функций в Matlab. Вычисление производных. M-файлы (файлы-сценарии). Метод деления

1.

Практическая работа № 2
Построение графиков функций в Matlab. М-файлы (файлы-сценарии).
Метод деления пополам для решения нелинейных уравнений
1. Построение графиков функций в Matlab
Рассмотрим простейшие графические средства Matlab.
Matlab позволяет строить двумерные и трехмерные графики функций, заданных в
аналитическом виде, в виде векторов и матриц, дает возможность построения множества
функций на одном графике: позволяет представлять графики разными цветами, типами
точек и линий и в различных системах координат.
Основными функциями двухмерной графики являются: plot(x, y), plot(x, y, s), где х –
аргумент функции, задаваемой в виде вектора; у – функция, представленная в
аналитическом виде или в виде вектора или матрицы; s – вектор стилей графика;
константа, определяющая цвет линий графика, тип точек и тип линий.
В таблице приведены некоторые возможные значения s:
вид кривой
символы
цвет
– сплошная
r красный
.
-- штриховая
g зеленый
+
: из точек
b синий
*
-. Штрих-пунктир
w белый
o
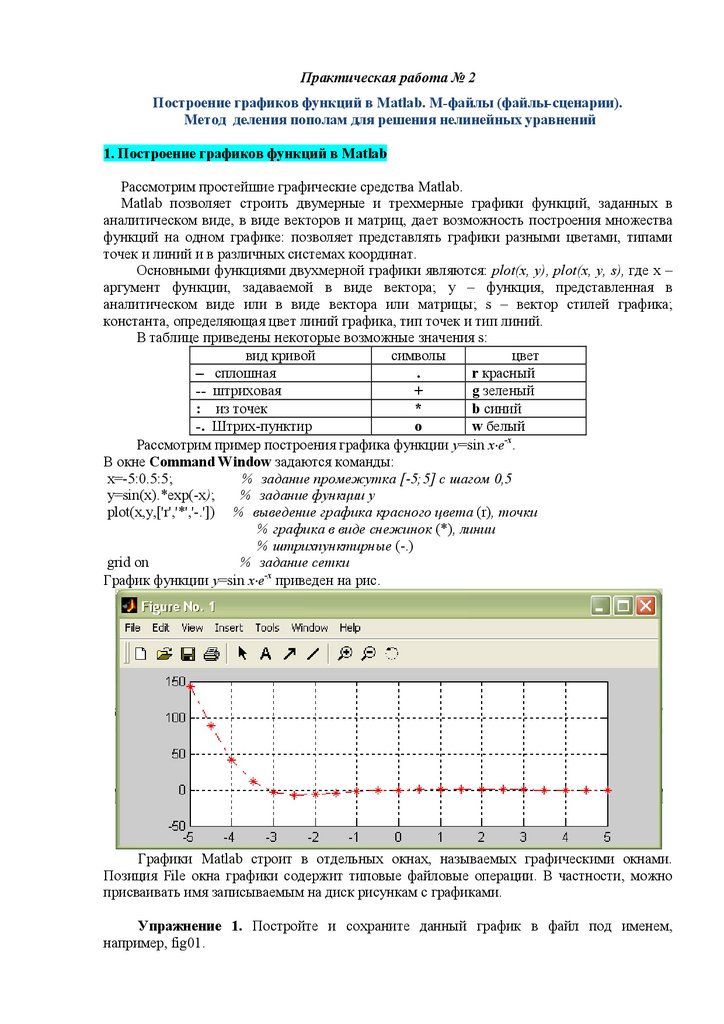
Рассмотрим пример построения графика функции у=sin x e-x.
В окне Command Window задаются команды:
x=-5:0.5:5;
% задание промежутка [-5;5] с шагом 0,5
y=sin(x).*exp(-x);
% задание функции у
plot(x,y,['r','*','-.']) % выведение графика красного цвета (r), точки
% графика в виде снежинок (*), линии
% штрихпунктирные (-.)
grid on
% задание сетки
График функции у=sin x e-x приведен на рис.
Графики Matlab cтроит в отдельных окнах, называемых графическими окнами.
Позиция File окна графики содержит типовые файловые операции. В частности, можно
присваивать имя записываемым на диск рисункам с графиками.
Упражнение 1. Постройте и сохраните данный график в файл под именем,
например, fig01.

2.

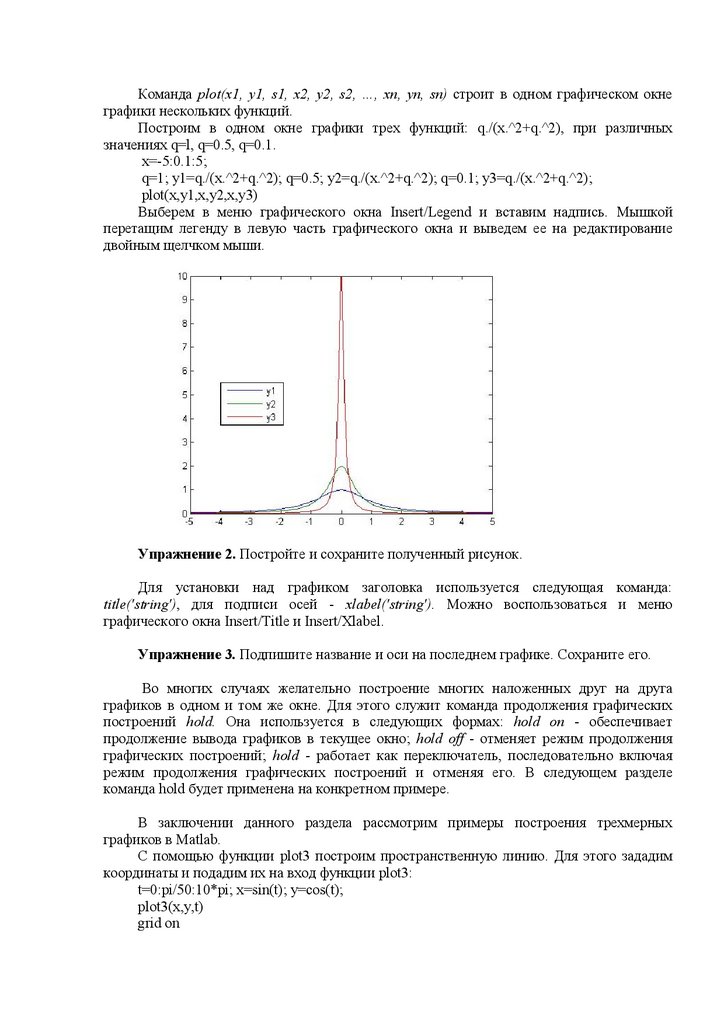
Команда plot(x1, y1, s1, x2, y2, s2, …, xn, yn, sn) строит в одном графическом окне
графики нескольких функций.
Построим в одном окне графики трех функций: q./(x.^2+q.^2), при различных
значениях q=l, q=0.5, q=0.1.
x=-5:0.1:5;
q=1; y1=q./(x.^2+q.^2); q=0.5; y2=q./(x.^2+q.^2); q=0.1; y3=q./(x.^2+q.^2);
plot(x,y1,x,y2,x,y3)
Выберем в меню графического окна Insert/Legend и вставим надпись. Мышкой
перетащим легенду в левую часть графического окна и выведем ее на редактирование
двойным щелчком мыши.
Упражнение 2. Постройте и сохраните полученный рисунок.
Для установки над графиком заголовка используется следующая команда:
title('string'), для подписи осей - xlabel('string'). Можно воспользоваться и меню
графического окна Insert/Title и Insert/Xlabel.
Упражнение 3. Подпишите название и оси на последнем графике. Сохраните его.
Во многих случаях желательно построение многих наложенных друг на друга
графиков в одном и том же окне. Для этого служит команда продолжения графических
построений hold. Она используется в следующих формах: hold on - обеспечивает
продолжение вывода графиков в текущее окно; hold off - отменяет режим продолжения
графических построений; hold - работает как переключатель, последовательно включая
режим продолжения графических построений и отменяя его. В следующем разделе
команда hold будет применена на конкретном примере.
В заключении данного раздела рассмотрим примеры построения трехмерных
графиков в Matlab.
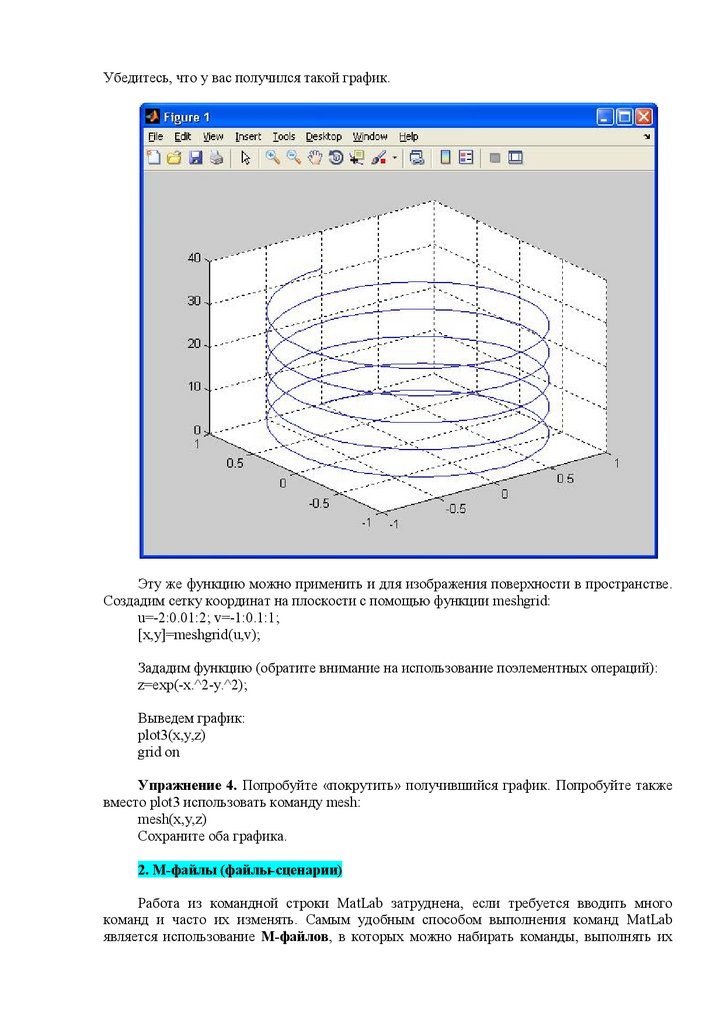
С помощью функции plot3 построим пространственную линию. Для этого зададим
координаты и подадим их на вход функции plot3:
t=0:pi/50:10*pi; x=sin(t); y=cos(t);
plot3(x,y,t)
grid on

3.

Убедитесь, что у вас получился такой график.
Эту же функцию можно применить и для изображения поверхности в пространстве.
Создадим сетку координат на плоскости с помощью функции meshgrid:
u=-2:0.01:2; v=-1:0.1:1;
[x,y]=meshgrid(u,v);
Зададим функцию (обратите внимание на использование поэлементных операций):
z=exp(-x.^2-y.^2);
Выведем график:
plot3(x,y,z)
grid on
Упражнение 4. Попробуйте «покрутить» получившийся график. Попробуйте также
вместо plot3 использовать команду mesh:
mesh(x,y,z)
Сохраните оба графика.
2. М-файлы (файлы-сценарии)
Работа из командной строки MatLab затруднена, если требуется вводить много
команд и часто их изменять. Самым удобным способом выполнения команд MatLab
является использование М-файлов, в которых можно набирать команды, выполнять их

4.

все сразу или частями, сохранять в файле и использовать в дальнейшем. Для работы с Мфайлами предназначен редактор М-файлов. При помощи этого редактора можно создавать
собственные функции и вызывать их, в том числе и из командной строки.
Рассмотрим работу команды hold, создав (для нашего удобства) m-файл.
В окне редактора М-файлов в меню File, в пункте New выберем подпункт M-file.
Наберем в редакторе команды:
x = -3:0.01:3;
f =0.5*x+0.1*sin(25*x);
plot(x, f)
hold on
g = abs(x);
plot(x, g)
Упражнение 5. Сохраните файл, например, под именем graph.m, выбрав пункт
Save as меню File редактора.
Для запуска команд на выполнение можно нажать F5 или выбрать Debug/Run. Если
теперь нужно построить график cos(x) вместо abs(x), достаточно исправить
соответствующую строчку и запустить выполнение команд.
Упражнение 6. Исправьте и сохраните полученный рисунок.
Бывает, что в одном окне надо расположить несколько координатных осей с
различными графиками без наложения их друг на друга. Для этого используются команда
subplot, применяемые перед построением графиков: subplot(m,n,p) - разбивает графическое
окно на m х n подокон, m - число подокон по горизонтали, n - число подокон по вертикали,
а р - номер подокна, в которое будет выводиться текущий график (подокна отсчитываются
последовательно по строкам). Для всех графиков возможна индивидуальная установка
дополнительных объектов, например титульных надписей, подписей по осям и т.д.
Наберем в редакторе команды, приводящие к построению двух графиков в одном
графическом окне:
x = [0:0.1:7];
f = exp(-x);
subplot(1, 2, 1)
plot(x, f)
g = sin(x);
subplot(1, 2, 2)
plot(x, g)
Отдельные блоки М-файла можно снабжать комментариями, которые пропускаются
при выполнении, но удобны при работе с М-файлом. Комментарии в MatLab начинаются
со знака процента и автоматически выделяются зеленым цветом, например:
% построение графика sin(x)
Упражнение 7. Добавьте комментарии и сохраните m-файл.
Закройте графическое окно Figure 1. Выделите при помощи мыши, удерживая левую
кнопку, или клавишами со стрелками при нажатой клавише Shift, четыре команды, и
выполните их, нажав клавишу F9. В графическом окне должен появиться только один
график.
Упражнение 8. Сохраните полученный рисунок.

5.

В редакторе М-файлов может быть одновременно открыто несколько файлов.
Переход между файлами осуществляется при помощи закладок с именами файлов,
расположенных внизу окна редактора. Заметим, что в этой работе мы имели дело только с
так называемыми Script-M-файлами или файлами-сценариями, не имеющими входных
параметров. С другим типом М-файлов – файлами-функциями мы познакомимся в
следующей лабораторной работе.
3. Метод деления пополам для решения нелинейных уравнений
Решение уравнения f(x)=0 состоит из двух этапов:
1. Отделение корней (на данном этапе мы находим, сколько корней, на каких
промежутках, какой кратности имеет уравнение).
2. Уточнение корней (находим значение корней с заданной точностью).
Отделение корней
– процедура нахождения отрезков, на которых уравнение имеет только одно решение. В
большинстве случаев отделение корней можно провести графически. В сомнительных
случаях графическое отделение корней подкрепляется аналитически, с помощью
следующих положений:
1. Если непрерывная функция f(x) принимает на концах отрезка [a,b] значения
разных знаков, то уравнение f(x)=0 имеет на этом отрезке по крайней мере один корень;
2. Если к тому же f(x) строго монотонна, то корень на отрезке единственный.
3
Пример: Рассмотрим функцию y x x 1 .
При x=1 она принимает отрицательное значение y=-1. При x=2 – положительное
значение y=5. Значит, на отрезке [1,2] функция имеет, по крайней мере, один корень.
2
Далее, поскольку производная y ' 3 x 1 0 при x 1, 2 , то функция строго
возрастает на всем отрезке и, следовательно, имеет ровно один корень.
Наши рассуждения можно подкрепить графически.
Зададим рассматриваемую функцию в Matlab с использованием оператора @ (т.е.
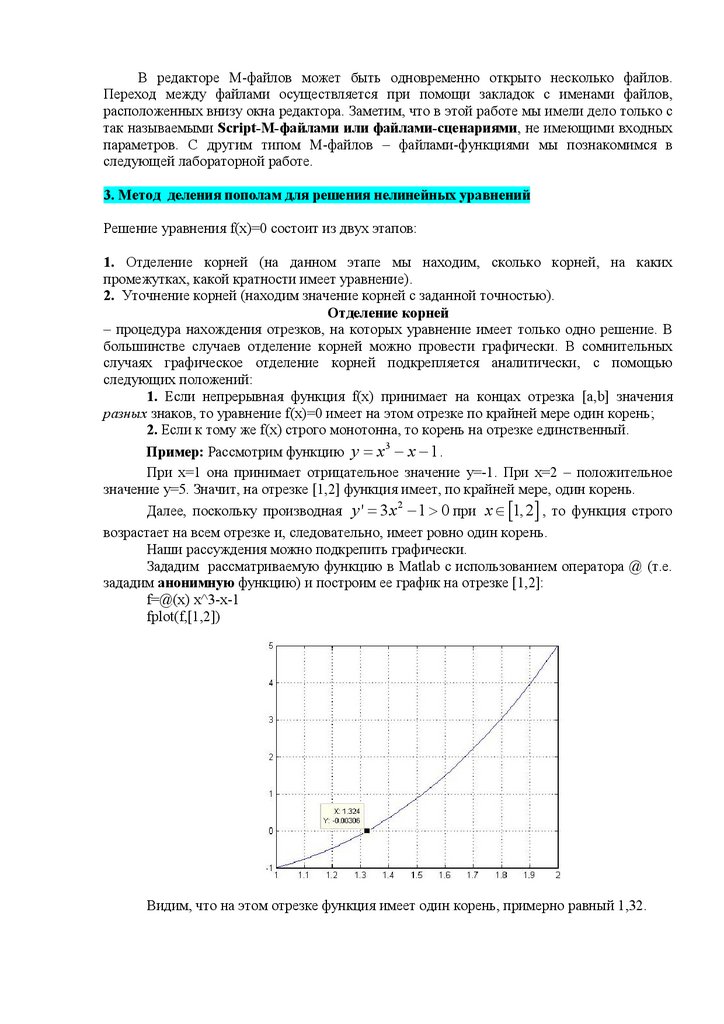
зададим анонимную функцию) и построим ее график на отрезке [1,2]:
f=@(x) x^3-x-1
fplot(f,[1,2])
Видим, что на этом отрезке функция имеет один корень, примерно равный 1,32.

6.

9. Покажите (аналитически и графически), что функция
y cos 2 x x 5 имеет один корень на отрезке [5,6].
Уточнение корней
После того, как все корни отделены, их требуется уточнить, т.е. найти их значения
с заданной точностью. Рассмотрим метод деления пополам уточнения корней.
Упражнение
Метод дихотомии (деления пополам, бисекции)
Пусть уравнение f(x)=0 имеет на отрезке [a,b] единственный корень, причем
функция f(x) на данном отрезке непрерывна.
Разделим отрезок [a,b] пополам точкой =
. Если ( ) ≠ 0, то возможны два
случая:
1. Функция f(x) меняет знак на отрезке [a,c].
2. Функция f(x) меняет знак на отрезке [c,b].
Выбирая в каждом случае тот отрезок, на котором функция меняет знак, и продолжая
процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка,
содержащего корень.
За приближенное значение корня можно принять середину последнего отрезка.
Погрешность определения корня при этом не превышает половины длины
последнего отрезка. Таким образом, для заданной точности вычисления следует вести до
тех пор, пока длина нового отрезка не станет меньше 2 .
3
Пример: Уточним корень функции y x x 1 . В прошлом примере мы
выяснили, что у нее есть ровно 1 корень на отрезке [1,2]. Зададимся точностью = 0.1.
Ясно, что f(1) < 0, f(2) > 0.
Шаг 1. Найдем середину отрезка [1,2]: c = 1.5
Определим знак функции в этой точке: f(1.5) > 0.
Итак, функция меняет знак на отрезке [1,1.5]. Это наш новый интервал
локализации корня. Длина интервала - 0,5 - больше, чем 2 . Продолжаем итерации.
Шаг 2. Находим середину нового интервала: : c = 1.25.
Определим знак функции в этой точке: f(1.25) < 0.
Итак, функция меняет знак на отрезке [1.25,1.5].
Удобно оформить наши рассуждения в виде таблицы.
+
Номер итерации
Знак Знак
=
( ) ( )
2
0
1
2
+
1.5
1
1
1.5
+
1.25
2
1.25 1.5
+
1.375
3
1.25 1.375 +
1.313
( )
+
+
-
−
1
0.5
0.25
0.125
Поскольку длина последнего интервала | − | = 0.125 < 2 = 0.2, вычисления
можно остановить.
.
Приближенное значение корня - 1.313. Гарантируемая точность = 0.06.
Упражнение 10. Найдите корень (вручную!) уравнения cos 2 x x 5 0 на
отрезке [5,6] с точностью.
= 0.1.