ОСН_МАТ_МОД_03_Решение_Нелин_Уравнений

1.

НЕЛИНЕЙНЫЕ И ТРАНСЦЕНДЕНТНЫЕ УРАВНЕНИЯ
И ИХ СИСТЕМЫ
Нелинейные уравнения содержат произведения искомых переменных либо
их степени выше первой. Такие уравнения могут иметь один, несколько либо
бесконечное множество корней. Поиск решений нелинейных уравнений бывает
чрезвычайно затруднительным. Рассмотрим одну из задач такого характера:
Задача 2
Найти корни полинома заданного выражением F ( x) a x b x c x d
если коэффициенты принимают следующие значения: а = 1, в = - 6 , с =
21 и d = -52.
Численное решение такого типа уравнений проводят в два этапа. На первом
этапе необходимо отделить корни уравнения, т. е. найти такие интервалы
изменения переменной х, где расположен только один корень.
По сути дела, на этом этапе находят приближенные значения корней, с
погрешностью, задаваемой длиной каждого интервала. На втором этапе
проводят уточнение отделенных корней, т. е. находят корни с заданной
точностью, для этого известен ряд алгоритмов.
3
2
Графический (или табличный) способ отделения корней уравнения
используется когда отсутствует информация о расположении корней. В
интересующей нас области изменения x [x0 , xn] при фиксированных
параметрах задачи вычисляют ряд значений левой части уравнения и строят
график.
1

2.

СРЕДСТВА MATHCAD ДЛЯ РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
Вычислить корни уравнения в среде MathCad можно с помощью встроенной
функции root(expr,var,[xmin,xmax]), где expr – выражение, var – переменная,
xmin и xmax – границы диапазона, внутри которого ищутся корни
(необязательные параметры).
Функция polyroots(v) позволяет найти корни полинома, здесь v – вектор
коэффициентов. Коэффициенты в векторе v располагаются по мере роста
степени аргумента.
Функция root(expr,var,[xmin,xmax]) работает по итерационному механизму
вычислений и использует при этом значение встроенной переменной TOL,
которая задает погрешность вычислений (допуск сходимости). Значение
переменной TOL, используемое средой MathCad по умолчанию равно 0,001.
В случае необходимости пользователь может присвоить переменной TOL
другое значение. Для работы функций, использующих итерационный механизм
вычислений, необходимо задавать начальное приближение искомой
величины. Практическое использование данных функций рассмотрим на
примере решения задачи 2.
Поскольку пользователь изначально не имеет никакой информации о
расположении корней, необходимо графически представить зависимость чтобы
наглядно определить количество и расположение корней.
2

3.

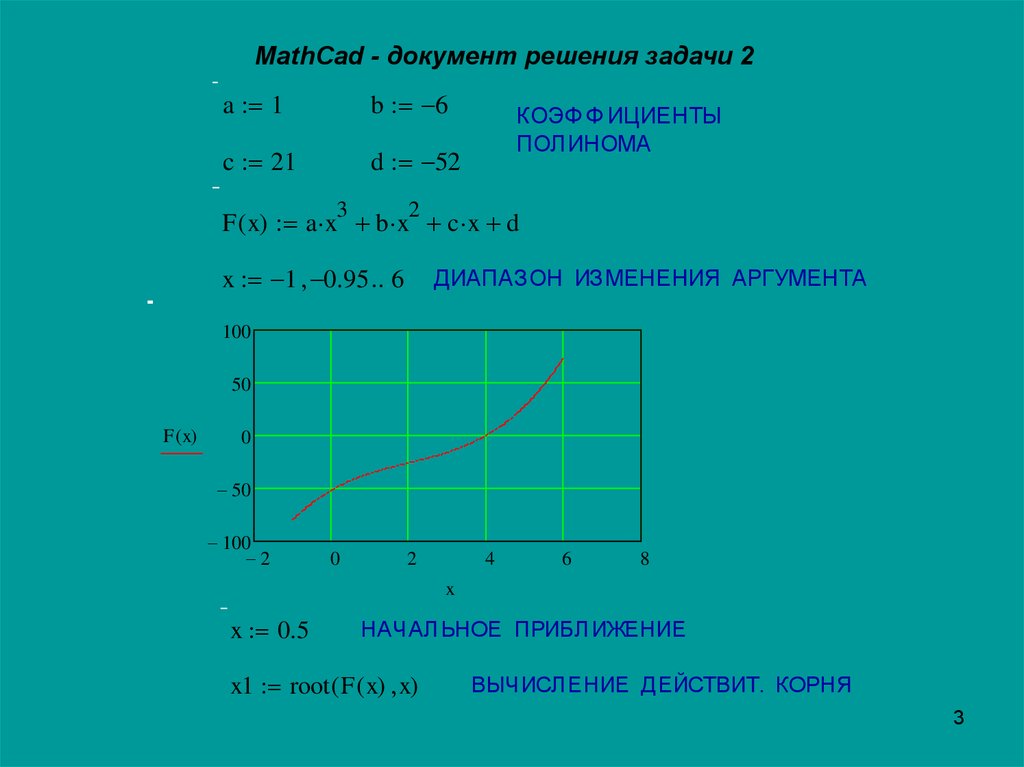
MathCad - документ решения задачи 2
a 1
b 6
c 21
d 52
3
КОЭФ Ф ИЦИЕНТЫ
ПОЛИНОМА
2
F ( x) a x b x c x d
x 1 0.95 6
ДИАПАЗОН ИЗМЕНЕНИЯ АРГУМЕНТА
100
50
F ( x)
0
50
100
2
0
2
4
6
8
x
x 0.5
НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ
x1 root ( F ( x) x)
ВЫЧИСЛЕНИЕ ДЕЙСТВИТ. КОРНЯ
3

4.

x1 4
ДЕЙСТВИТЕЛЬНЫЙ. КОРЕНЬ
ВЫЧИСЛЕНИЕ ОСТАЛЬНЫХ ( ВОЗМОЖНО КОМПЛЕКСНЫХ ) КОРНЕЙ
i
1
x 1 1 i
F ( x) x
x x1
НОВОЕ НАЧАЛЬНОЕ ПРИБЛИЖЕНИЕ
x2 root
ВЫЧИСЛЕНИЕ ВТОРОГО КОРНЯ
x2 1 3.464i
ВТОРОЙ КОРЕНЬ
F ( x)
x
( x x1) ( x x2)
x3 root
x3 1 3.464i
ТРЕТИЙ КОРЕНЬ
4

5.

При поиске второго корня заданного уравнения вместо F(x) была
подставлена функция F(x) делённая на x – x1, что позволило учесть тот факт,
что корень x1 уже найден.
При решении данной задачи в программе вычислений новое значение
переменной TOL не задавалось, т.е. использовалось значение, установленное
по умолчанию. Оно и определяет собой точность найденного корня.
Найдя корни уравнения необходимо выполнить их проверку.
Поскольку функция, приведенная в задаче 2 представляет собой полином, то
его корни с успехом могут быть найдены с помощью функции polyroots :
MathCad программа решения задачи 2 с помощью функции polyroots
52 d
c
21
V
6 b
a
1
X polyroots ( V)
1 3.464i
X 1 3.464i
4
5

6.

Уравнения типа f ( x, p1 , p2 ,..., pn ) 0 , где f(x) - некоторая функция, а p1, p2,…,
pn – параметры называются трансцендентными. Аналитическое решение таких
уравнений найти не удаётся, однако можно найти их численное решение,
причём со сколь угодно высокой точностью.
Задача 2 m
Определить при каком значении переменной x значение функции f(x)
будет равно 2. Известно, что f ( x) k x 2 exp a
, k =1.5, a = 3.3, c =
0.25 .
c x
Запишем наше уравнение в другом виде:
a
k x 2 exp
f0 0
c
x
Для решения задачи 2m помимо функции root можно воспользуемся
функцией Find, которая предназначена для решения систем линейных и
нелинейных алгебраических уравнений.
Данная функция работает со служебным словом Given за которым должны
следовать уравнения, подлежащие решению. Уравнения должны быть записаны
как булевы выражения.
MathCad - документ решения задачи 2 m
6

7.

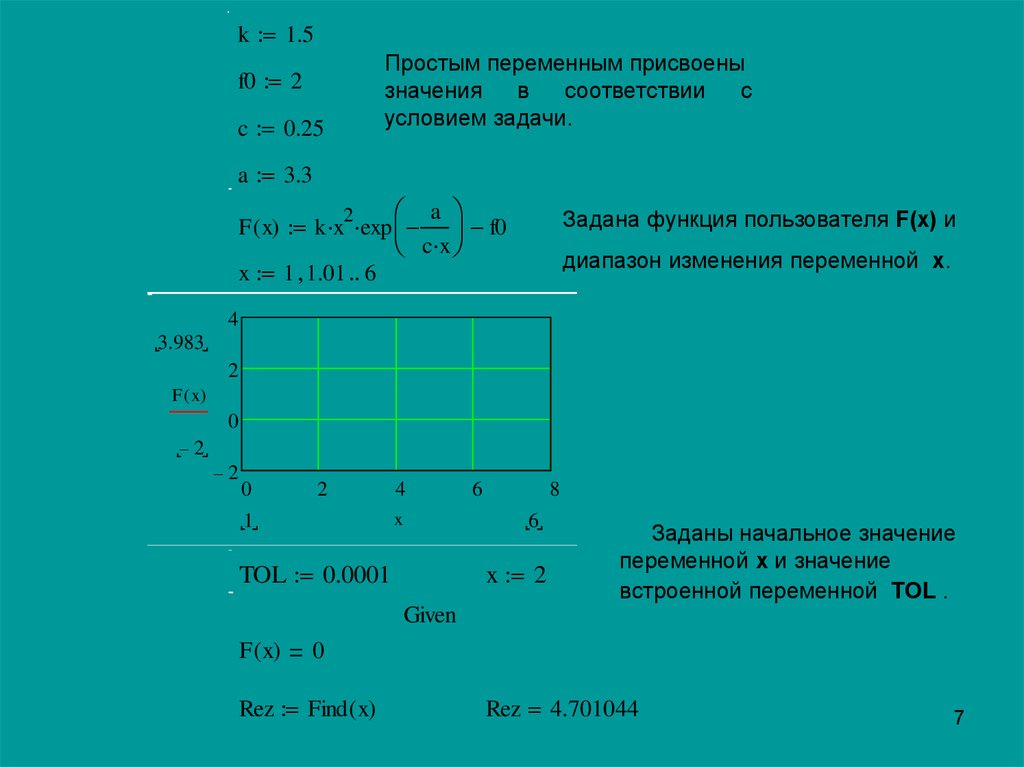
k 1.5
Простым переменным присвоены
значения
в
соответствии
с
условием задачи.
f0 2
c 0.25
a 3.3
a f0
c
x
F ( x) k x exp
Задана функция пользователя F(x) и
x 1 1.01 6
диапазон изменения переменной x.
2
4
3.983
2
F ( x)
0
2
2
0
2
4
x
1
6
8
6
TOL 0.0001
x 2
Заданы начальное значение
переменной x и значение
встроенной переменной TOL .
Given
F ( x)
0
Rez Find ( x)
Rez 4.701044
7

8.

Проанализировав ход кривой на графике, было установлено, что корень
один, а его величина больше 4, но меньше 5. Далее было задано начальное
приближение (x := 2), которое выбирается пользователем из области
определения функции, и соответствующее значение переменной TOL.
Получив решение уравнения, необходимо выполнить проверку результата,
чтобы убедиться, что погрешность вычислений на самом деле меньше
заданной пользователем.
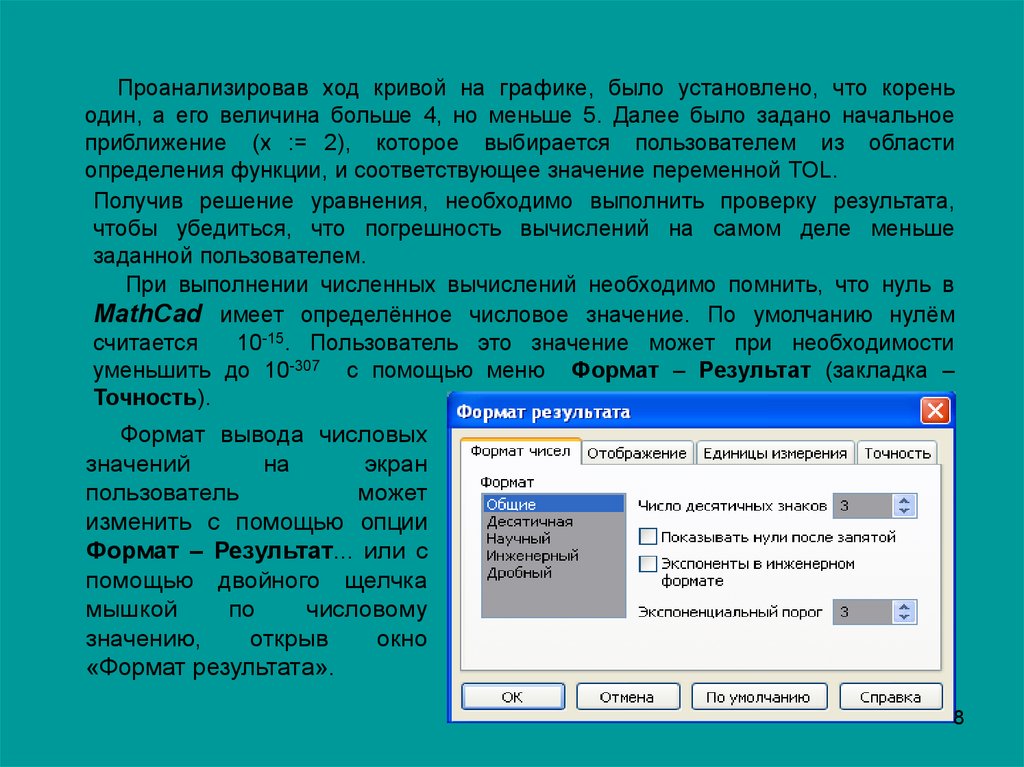
При выполнении численных вычислений необходимо помнить, что нуль в
MathCad имеет определённое числовое значение. По умолчанию нулём
считается
10-15. Пользователь это значение может при необходимости
уменьшить до 10-307 с помощью меню Формат – Результат (закладка –
Точность).
Формат вывода числовых
значений
на
экран
пользователь
может
изменить с помощью опции
Формат – Результат... или с
помощью двойного щелчка
мышкой
по
числовому
значению,
открыв
окно
«Формат результата».
8

9.

Окно «Формат результата» содержит четыре закладки, пользуясь которыми
можно изменить вид представления числовых значений на экране.
9