Практическое задание «Решение уравнений средствами Mathcad»

1.

Практическое задание
«РЕШЕНИЕ УРАВНЕНИЙ
СРЕДСТВАМИ MATHCAD»
1

2.

Численное решение нелинейного уравнения
Для простейших уравнений вида f(x) = 0
решение в MathCad находится с помощью
функции root(f(x),x), где f(x) – выражение, равное
нулю, x – аргумент, варьируя который, система
ищет значение.
Если задан
root(f(x),x,a,b).
интервал
поиска
корней:
2

3.

Начальные приближения:
Известны из физического смысла задачи;
Известны из решения аналогичной задачи при
других исходных данных;
Найдены графическим способом.
Функция solve:
Так же для решения уравнений в MathCad
используется функция solve.
f(x)=0 solve,x
3

4.

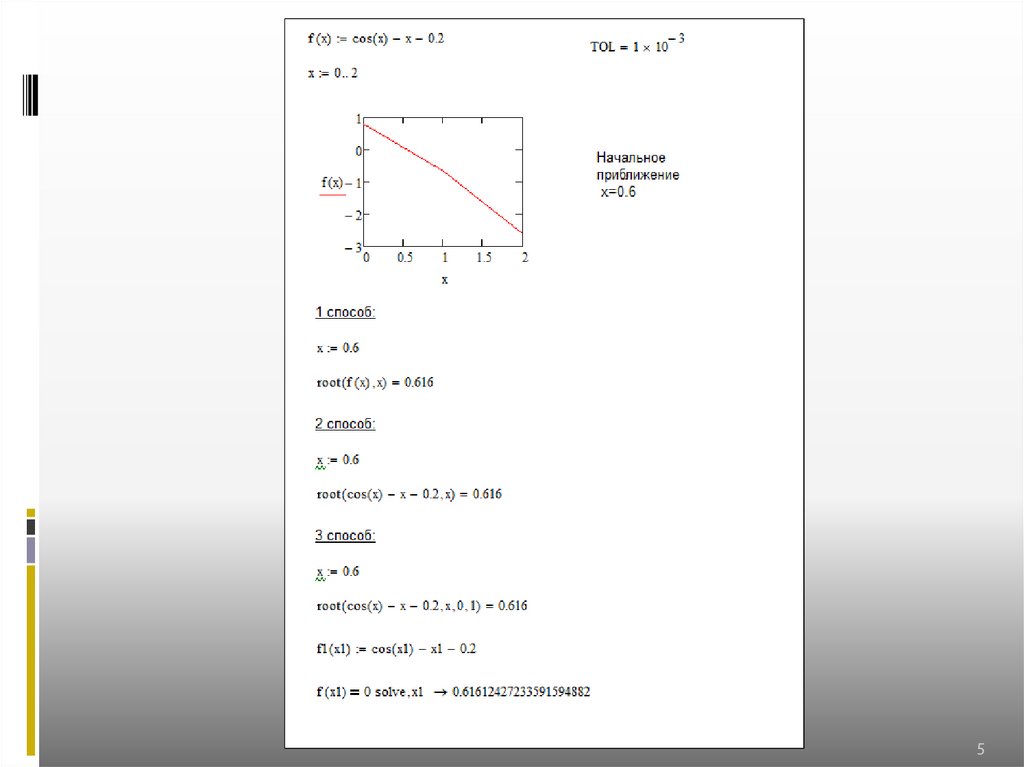
Пример – решение уравнения cos(x)=x+0.2 в MathCad
1. Графическое решение
2. Решение с помощью root
3. Решение с помощью solve
Знак присвоить можно ставить с помощью «shift:»
4

5.

5

6.

Нахождение корней полинома
Для
нахождения
корней
выражения,
имеющего вид
vnxn + ... + v2x2 + v1x + v0,
лучше использовать функцию polyroots, нежели
root.
Возвращает корни полинома степени n.
Коэффициенты полинома находятся в векторе v
длины n + 1. Возвращает вектор длины n,
состоящий из корней полинома.
6

7.

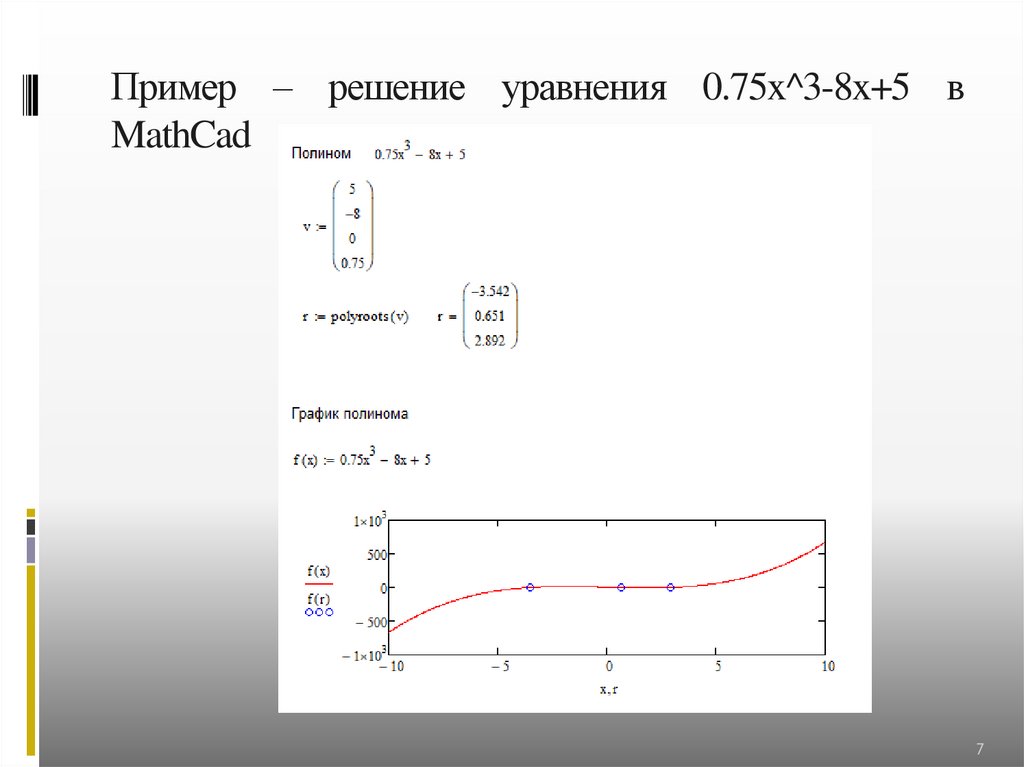
Пример – решение уравнения 0.75x^3-8x+5 в
MathCad
7

8.

Решение систем уравнений
Для решения системы уравнений необходимо
выполнить следующее:
Задать
начальное приближение для всех
неизвестных, входящих в систему уравнений.
Mathcad решает систему с помощью итерационных
методов.
Напечатать ключевое слово Given. Оно указывает
Mathcad, что далее следует система уравнений.
Введите уравнения и неравенства в любом
порядке. Введите любое выражение, которое
включает функцию Find
8

9.

Решение систем уравнений
Функция Find возвращает точное решение
системы уравнений. Число аргументов должно быть
равно числу неизвестных.
Ключевое
слово
Given,
уравнение
и
неравенства, которые следуют за ним, и какое-либо
выражение, содержащее функцию Find, называют
блоком решения уравнений.
9

10.

Пример – решение системы уравнений в MathCad
10

11.

Решение систем уравнений
Рассмотрим
систему
алгебраических
уравнений
неизвестных х1, х2, …, хn:
n
линейных
относительно
n
a11 x1 a12 x2 ... a1n xn b1 ,
a x a x ... a x b ,
21 1
22 2
2n n
2
. . . . . . . .
an1 x1 an 2 x2 ... ann xn bn .
В соответствии с правилом умножения матриц
рассмотренная система линейных уравнений может
быть записана в матричном виде Ах = b.
11

12.

Где А – матрица коэффициентов (матрица
системы), b – матрица правой части, x –
матрица неизвестных (решение системы)
a11 a12
a
a
A 21 22
a
n1 an 2
a1n
a2 n
,
ann
1
x1
x
x 2 ,
...
x
n
b1
b
b 2
...
b
n
1
A Ax A b,
1
x A b.
Системы линейных уравнений удобно решать
с помощью функции lsolve.
lsolve(А, b)
12

13.

Пример – решение системы уравнений в MathCad
13

14.

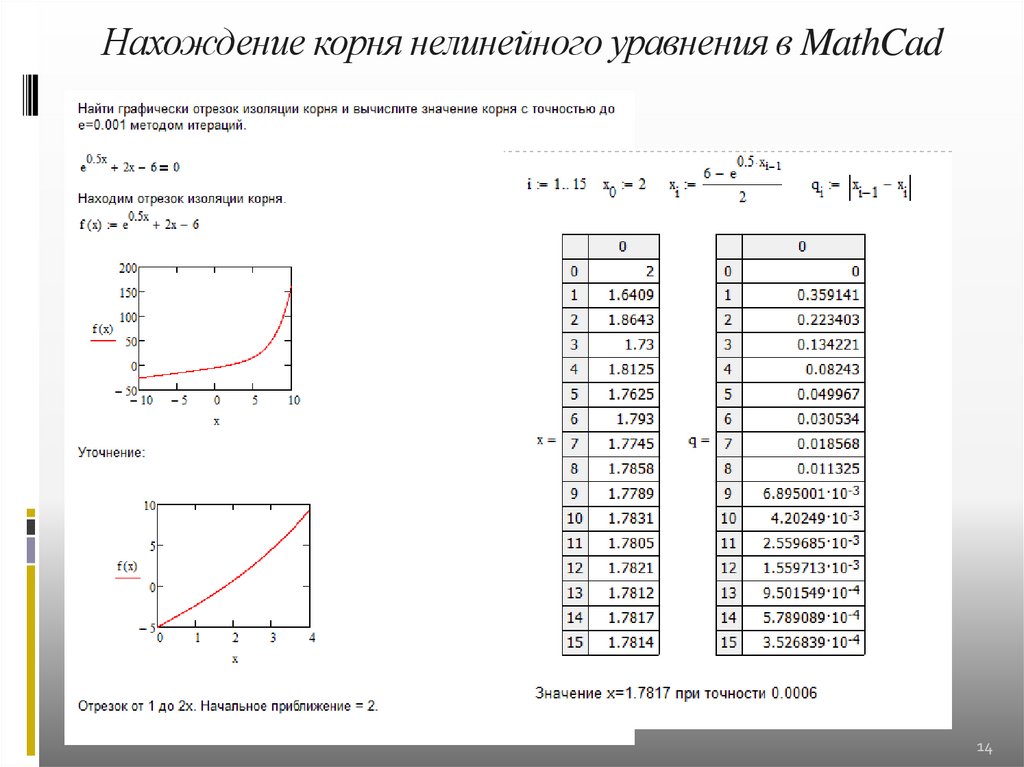
Нахождение корня нелинейного уравнения в MathCad
14

15.

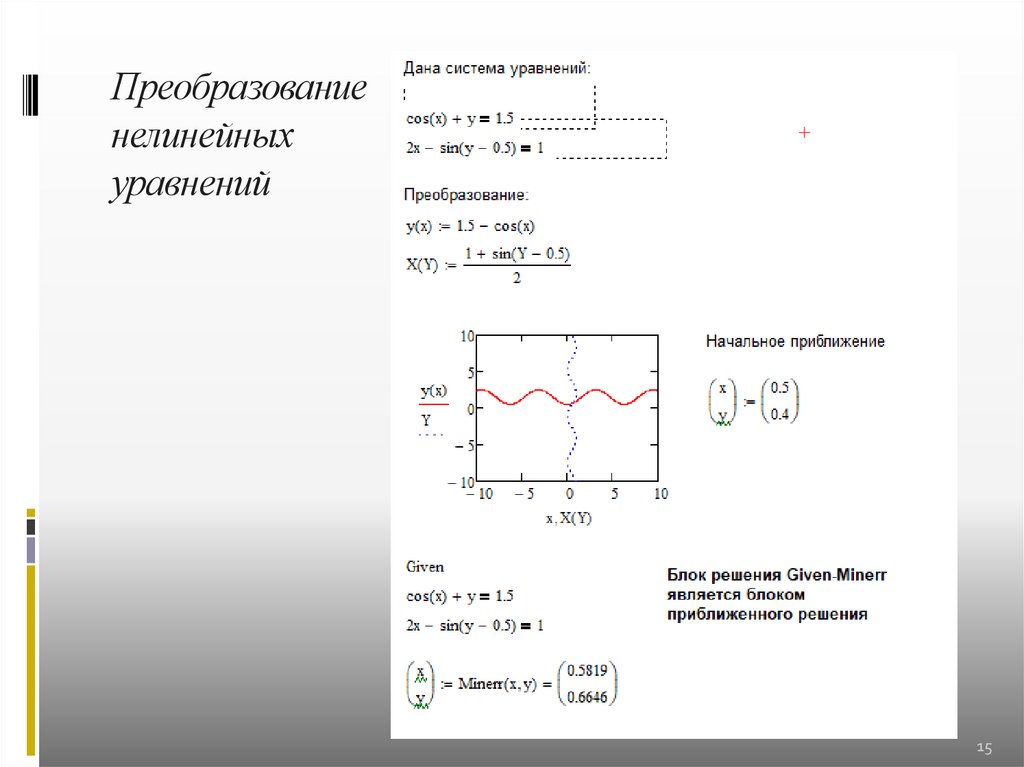
Преобразование
нелинейных
уравнений
15