Химическая кинетика и катализ

1.

Химическая кинетика и катализ
Законы химической термодинамики позволяют определить
направление и предел протекания возможного при данных
условиях химического процесса, а также его энергетический эффект
(∆rН, ∆rU, ∆rS, …)
Однако, термодинамика не может ответить на
вопросы о том, как осуществляется данный процесс и с
какой скоростью он протекает.
Кроме того, многие процессы протекают через
несколько
стадий
с
образованием
ряда
промежуточных и конечных продуктов.
Эти вопросы – механизм и скорость
химической реакции – являются предметом
изучения химической кинетики
Химическая кинетика. Лекция 1.
1

2.

«Термодинамика» и «Кинетика»
• Известно, что возможность или невозможность протекания
химического
превращения
определяется
изменением
термодинамических потенциалов (энергий Гиббса ΔG и Гельмгольца
ΔA).
• Однако в ряде случаев даже процессы, возможные термодинамически,
практически не совершаются из-за ничтожно малых скоростей.
Пример: смесь водорода с кислородом, даже в стехиометрическом для
полного сгорания соотношении (т.н. гремучий газ) , может «мирно»
существовать бесконечно долго, хотя ΔG этой реакции <<0. Однако она
способна взорваться от самого слабого источника энергии (нагрев, искра
и т.д.)
В связи с этим установление кинетических закономерностей
является необходимым для определения возможности реального
осуществления химической реакции.
Химическая кинетика. Лекция 1.
2

3.

Химическая кинетика и катализ
Химическая кинетика – раздел физической химии,
изучающий закономерности протекания физико-химических
процессов во времени.
Цель
кинетических
исследований
заключается
в
следующем:
изучить зависимость скорости реакции от концентрации
реагентов, температуры, свойств среды, электромагнитного
излучения, катализатора и других факторов;
установить стехиометрический механизм химической реакции,
т.е. определить число элементарных стадий сложного процесса и
установить природу образующихся при этом промежуточных и
конечных продуктов;
выяснить взаимосвязь строения реагирующих молекул со
скоростью реакции и объяснить причины ее зависимости от
перечисленных выше факторов.
Химическая кинетика. Лекция 1.
3

4.

Химическая кинетика и катализ
В кинетических исследованиях решаются две основные
задачи.
Прямая кинетическая задача заключается в расчете
скорости реакции и текущих концентраций реагентов по
известному кинетическому уравнению. Такая задача обычно
решается в технологических исследованиях, имеющих цель
определить оптимальные условия проведения процесса, то
есть достигнуть максимальной производительности за
минимальный промежуток времени.
Обратная кинетическая задача ставится и решается в
кинетических исследованиях. Она состоит в разработке
кинетической модели реакции на базе ее стехиометрического
механизма и зависимости концентрации от времени для
исходных реагентов, промежуточных и конечных продуктов.
Химическая кинетика. Лекция 1.
4

5.

Скорость химической реакции
Определение (строгое):
Скорость химической реакции есть число
однотипных элементарных актов химической реакции, происходящих в
единицу времени в единице реакционного пространства (в единице
объема для гомогенных реакций или
на единице площади для
гетерогенных реакций)
Или: число пробегов реакции,
или количество вещества (израсходрованного или образовавшегося)
в единицу времени в единице реакционного пространства
n n
n
i i,0 i
i
i
Вспомним термин число
пробегов (пробег) реакции:
«+» - для продуктов,
«-» для исходных веществ
Для реакции:
n
n
n
n
1 2 3 4
1
2
3
4
Пример: СН + 2О → СО + 2Н О
4
nCH 4
1
2
2
nO2
2
2
nCO2
1
nH 2O
2
Химическая кинетика. Лекция 1.
5

6.

Скорость химической реакции
Определение (строгое): Скорость химической реакции есть число
однотипных
элементарных
актов
химической
реакции,
происходящих в единицу времени в единице реакционного
пространства (в единице объема для гомогенных реакций или на
единице площади для гетерогенных реакций)
Или: число пробегов реакции,
или количество вещества (израсходрованного или образовавшегося)
в единицу времени в единице реакционного пространства
Элементарной реакцией (стадией) называют совокупность
большого числа элементарных актов химического взаимодействия,
которые протекают с преодолением одного энергетического
барьера путем прямого превращения молекул исходных реагентов в
молекулы конечных продуктов реакции.
Химическая кинетика. Лекция 1.
6

7.

Скорость химической реакции
Согласно определению: r
или
r
Если объем V=const, то:
r
Тогда
1 d
1 dni
V d
i Vd
1 d
1 dni
S d
i Sd
«+» - для продуктов,
«-» для исходных веществ
dni
dCi , где Сi – концентрация.
V
1 dCi
i d
Скорость реакции не зависит от того, через концентрацию
какого вещества она выражена, т.е. для реакции:
r
1 dC1
1 dC2
1 dC3
1 dC4
1 d
2 d
3 d
4 d
Химическая кинетика. Лекция 1.
7

8.

Скорость химической реакции
dni
dCi , где Сi – концентрация.
V
«+» - для продуктов,
1 dCi
r
«-» для исходных веществ
i d
Итак, если объем V=const, то:
Тогда
Таким образом, для реакций, протекающих без изменения
объема (например в жидкой фазе):
скорость химической реакции r равна изменению
концентрации реагирующих веществ в единицу времени (с
учетом стехиометрии).
Вспомним, что понятие «производная» как раз и
характеризует скорость изменения функции, в данном случае –
концентрации.
Химическая кинетика. Лекция 1.
8

9.

Скорость химической реакции
.
Кроме величины скорости процесса, описываемой
уравнением (4.3), на практике используют понятие скорость
процесса по реагенту – ri.
dC
ri i
d
«+» - для продуктов,
«-» для исходных веществ
.
Связь величин r и ri отражает выражение:
r
1
1
1
1
r1 r2 r3 r4
1 2
3 4
Химическая кинетика. Лекция 1.
9

10.

Скорость химической реакции
r
1 dCi
i d
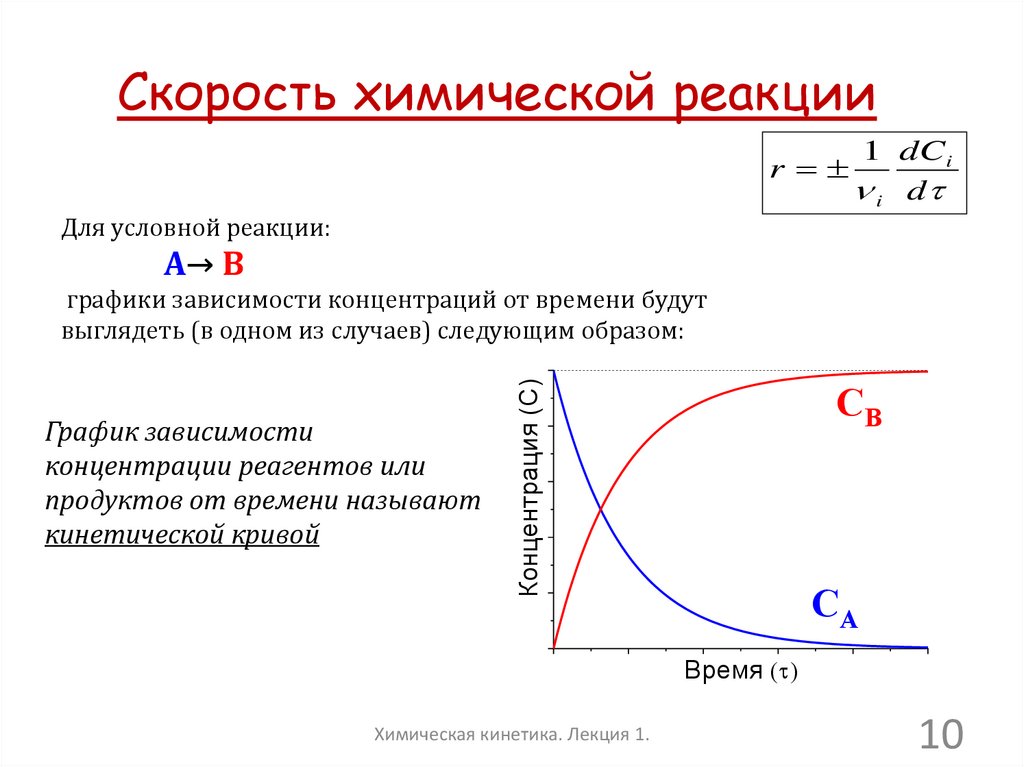
Для условной реакции:
А→ В
График зависимости
концентрации реагентов или
продуктов от времени называют
кинетической кривой
Концентрация (C)
графики зависимости концентраций от времени будут
выглядеть (в одном из случаев) следующим образом:
CB
CA
Время ( )
Химическая кинетика. Лекция 1.
10

11.

Скорость химической реакции
Определение истинной скорости реакции по
исходному реагенту и конечному продукту в
мономолекулярной реакции:
r
1 dCi
i d
Концентрация (C)
А→ В
a
b
CB
r = tga tgb
CA
Время ( )
Химическая кинетика. Лекция 1.
11

12.

Скорость химической реакции
От чего может зависеть скорость химической реакции?
Скорость химической реакции зависит от:
Природы реагирующих веществ
Концентраций реагирующих веществ
Температуры
Природы растворителя
Наличия катализатора
Других факторов - излучения, механических воздействий…
Химическая кинетика. Лекция 1.
12

13.

Скорость химической реакции
Рассмотрим пример:
Пусть при некоторых условиях скорость образования NO в
реакции
2 NOBr(г) → 2 dC
NO(г)
+ Br2(г)ммоль
NO
составила
d
0,16
л с
Поскольку νNO =+2, мы можем заключить, что скорость реакции
равна (давайте подсчитаем и дадим ответ):
1 dC NO
ммоль
r
0,080
2 d
л с
А поскольку νNOBr = -2, то cкорость расхода NOBr равна:
dC NOBr
ммоль
0,16
d
л с
Но скорость реакции при этом:
r
1 dC NOBr
2
d
0,080
ммоль
л с
Кстати, это равносильно скорости расхода NOBr 9.6 × 1016 молекул /(cм3 с).
Химическая кинетика. Лекция 1.
13

14.

Кинетический закон действующих масс
(К.З.Д.М.)
Химическая кинетика. Лекция 1.
14

15.

Закон действующих масс (З.Д.М.)
Термодинамический З.Д.М.
Кинетический З.Д.М.
касающийся состава реакционной
смеси в равновесном состоянии
касающийся уравнений
скорости для
элементарных реакций
(вспомните весенний семестр)
Для реакции:
ν1А1 + ν2А2 ↔ ν3А3 + ν4А4
P3 3 P4 4
1
2 KР
P1 P2
Эта дробь зависит только от:
• природы реагентов
и
•температуры
Химическая кинетика. Лекция 1.
15

16.

Кинетический закон действующих масс (К.З.Д.М.)
Одной из задач химической
кинетики является определение состава
реакционной смеси в любой момент
времени (!!!). Для этого необходимо знать
зависимость скорости реакции от текущих
концентраций.
Очевидно, что чем выше
концентрации реагирующих веществ, тем
выше скорость реакции.
В основе химической кинетики
лежит постулат, сформулированный
норвежскими учеными
Като Максимилианом Гульдбергом и
Петером Воге, вытекающий из
экспериментальных наблюдений,
сделанных в период между 1867 и 1879
годами.
Химическая кинетика. Лекция 1.
Cato Maximilian
Guldberg
(1836-1902)
Peter Waage
(1833 – 1900)
16

17.

Кинетический закон действующих масс (К.З.Д.М.)
Гульберг и Воге:
Для реакции:
ν1А1 + ν2А2 → продукты
«Скорость химической реакции пропорциональна
концентрациям реагирующих веществ в степенях, равных
их стехиометрическим коэффициентам», т.е.:
1
2
r k C A1 C A2
К примеру, для элементарной реакции типа
А+2В→продукты
кинетическое уравнение следует записать:
r kC1ACB2 kCACB2
Химическая кинетика. Лекция 1.
17

18.

Кинетический закон действующих масс (К.З.Д.М.)
Это может быть интересно!!!
Социофизика использует инструменты и
концепции из физики и физической химии для
описания некоторых аспектов социального и
политического поведения.
В ней предпринимаются попытки объяснить,
почему и как люди ведут себя во многом подобно
атомам, по крайней мере, в некоторых аспектах их
коллективной жизни.
Закон действующих масс (обобщенный, если
это необходимо) является основным инструментом
для получения «уравнения взаимодействий людей» в
социофизике.
Химическая кинетика. Лекция 1.
18

19.

Кинетический закон действующих
масс (К.З.Д.М.)
.
В общем случае КЗДМ записывается так:
r kCAn11 CAn22
где показатели степеней n1 и n2 – коэффициенты, называемые
частными порядками реакции
Химическая кинетика. Лекция 1.
19

20.

Кинетический закон действующих масс
νА A+νВ B→ продукты…
r kCAnA CBnB
Коэффициент k есть константа скорости химической реакции.
Константа k является коэффициентом пропорциональности
между скоростью реакции r и концентрациями Ci реагирующих
веществ.
Физический смысл:
Константа скорости химической реакции k численно равна
скорости реакции r при концентрациях реагирующих веществ
CA=CB=1
Константа скорости зависит от тех же факторов, что и
скорость реакции, но кроме(!!!):
• концентрации реагирующих веществ
и
• времени
Химическая кинетика. Лекция 1.
20

21.

Кинетический закон действующих масс
νА A+νВ B→ продукты…
r kCAnA CBnB
Молекулярность химической реакции
• Сумма стехиометрических коэффициентов
ν = (νА+ νВ)
называется молекуляностью химической реакции.
Молекулярность равна числу частиц, участвующих в одном акте
химического взаимодействия.,
Различают реакции:
o мономолекулярные
o бимолекулярные
o тримолекулярные
Примеры:
Br2 → Br ∙ + Br ∙
СН3Вr + КОН → СН3ОН + КВr
О2 + NО + NО → 2NО2
Химическая кинетика. Лекция 1.
21

22.

Кинетический закон действующих масс
νА A+νВ B→ продукты…
r kC C
nA
A
nB
B
Общий и частные порядки химической реакции
Сумма показателей в уравнении закона действующих масс (ЗДМ)
n= (nА+nВ)
называется общим порядком химической реакции;
• Показатели nА и nВ называются частными порядками реакции по
реагентам А и В
Важно помнить:
• Частные порядки реакции не всегда совпадают со
стехиометрическими коэффициентами. Их определяют только из
опыта.
• Общий порядок реакции может быть равен n= 0, 1, 2, 3.
• Но может иметь и дробные, и отрицательные значения.
• Порядок реакции характеризует кинетическое уравнение реакции,
а молекулярность – механизм реакции.
Химическая кинетика. Лекция 1.
22

23.

Кинетический закон действующих масс
νА A+νВ B→ продукты…
r kC C
nA
A
nB
B
Следует помнить, что
Закон действующих масс выполняется при определенных условиях,
которые для простой реакции заключаются в следующем:
1. Химическая реакция протекает достаточно медленно по сравнению с
физическими процессами обмена энергией между реагирующими
молекулами.
2. Изменение концентрации реагентов заметно не меняет свойства
среды (вязкость, полярность и т.д.) и физическое состояние реагентов.
3. Химическая реакция осуществляется только за счет тепловой
энергии. Если реакция протекает под влиянием электромагнитного
или радиационного излучений, электрического тока и т.д., то скорость
зависит от этих факторов, а закон действующих масс изменяется.
Химическая кинетика. Лекция 1.
23

24.

Реакции нулевого порядка
(n=0)
Математическое описание этих реакций простое.
Тем не менее, необходимо помнить, что реакции нулевого порядка это всегда сложные реакции!!!
Рассмотрим модельную реакцию:
k
A продукты...
По закону действующих масс: r kCAA
С учетом условия нулевого порядка nA= 0:
n
Итак,
r kCA0 k
r kCA0 k
dC A
Согласно определению скорости реакции: r
d
dC A
k
Объединив формулы:
d
Химическая кинетика. Лекция 1.
24

25.

Реакции нулевого порядка
(n=0)
dC A
k
d
Таким образом, скорость реакции нулевого
порядка постоянна во времени и не зависит
от концентрации реагирующих веществ.
Разделим переменные и проинтегрируем:
CA
dC kd
A
C A, 0
0
Получаем зависимость концентрации исходного реагента от времени:
C A C A , 0 k
В реакции нулевого порядка концентрация убывает пропорционально
времени реакции.
Химическая кинетика. Лекция 1.
25

26.

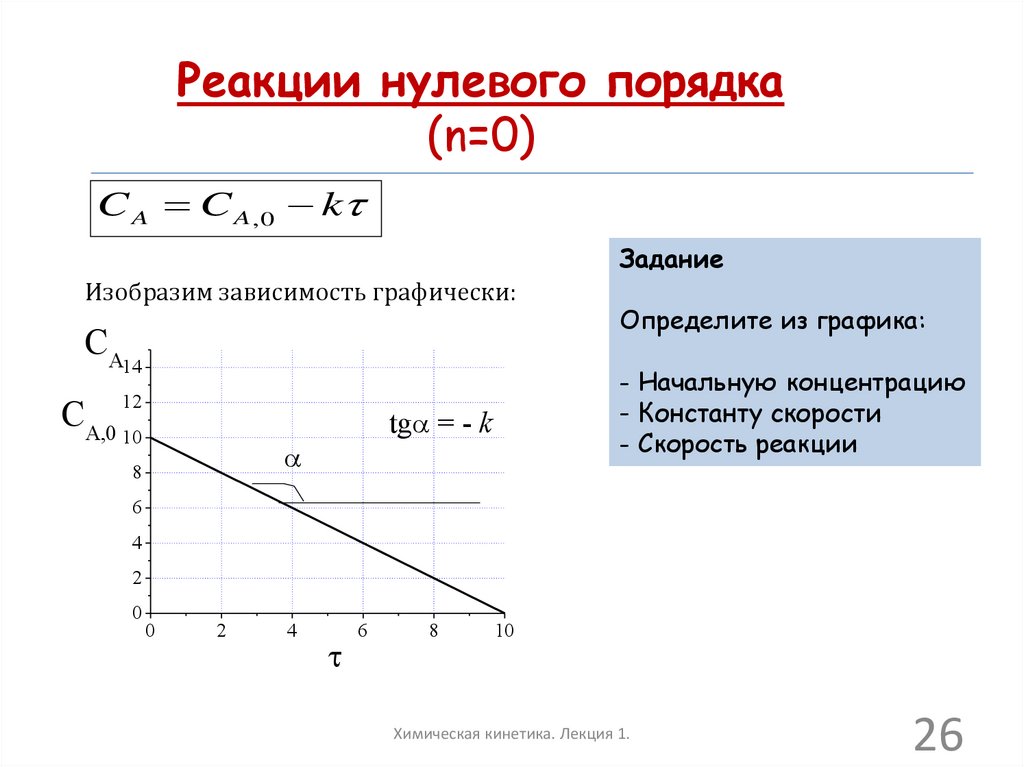
Реакции нулевого порядка
(n=0)
C A C A , 0 k
Задание
Изобразим зависимость графически:
CA
14
12
CA,0 10
- Начальную концентрацию
- Константу скорости
- Скорость реакции
tga = - k
a
8
Определите из графика:
6
4
2
0
0
2
4
6
8
10
Химическая кинетика. Лекция 1.
26

27.

Реакции нулевого порядка
(n=0)
Период полупревращения
Одной из величин, характеризующих скорость реакции является
период полупревращения (полураспада) τ1/2 , определяемое как время,
за которое реагирует половина исходного вещества.
При τ = τ1/2 СА=СА,0/2, тогда
C A, 0
2
C A , 0 k 1/ 2
Откуда:
1/ 2
C A,0
2k
Таким образом, для реакции нулевого порядка время полупревращения
прямо пропорционально начальной концентрации
Химическая кинетика. Лекция 1.
27

28.

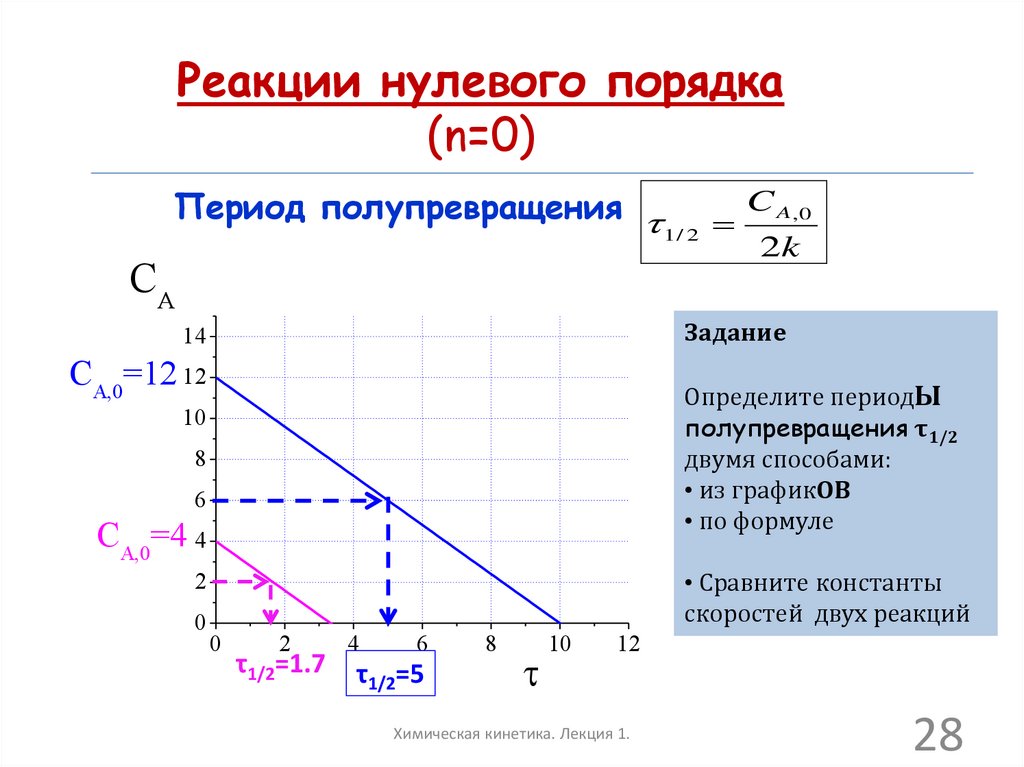
Реакции нулевого порядка
(n=0)
Период полупревращения
CA
2k
Задание
14
CA,0=12 12
Определите периодЫ
полупревращения τ1/2
двумя способами:
• из графикОВ
• по формуле
10
8
6
CA,0=4 4
• Сравните константы
скоростей двух реакций
2
0
1/ 2
C A,0
0
2
τ1/2=1.7
4
6
τ1/2=5
8
10
12
Химическая кинетика. Лекция 1.
28

29.

Реакции первого порядка
(n=1)
Теперь рассмотрим реакцию первого порядка.
k
A продукты...
По закону действующих масс:
r kCAn A
С учетом условия первого порядка nA= 1:
r kC1A
Итак, r kCA
Скорость реакции первого порядка прямо пропорциональна концентрации.
Согласно определению скорости реакции:
r
Объединив формулы:
dC A
d
dC A
kCA
d
Химическая кинетика. Лекция 1.
29

30.

Итак:
Реакции первого порядка
(n=1)
dC A
kCA
d
Разделим переменные и проинтегрируем:
CA
dC A
k d
CA
C A, 0
0
Получаем зависимость концентрации исходного реагента от времени:
ln C A ln C A , 0 k
Химическая кинетика. Лекция 1.
30

31.

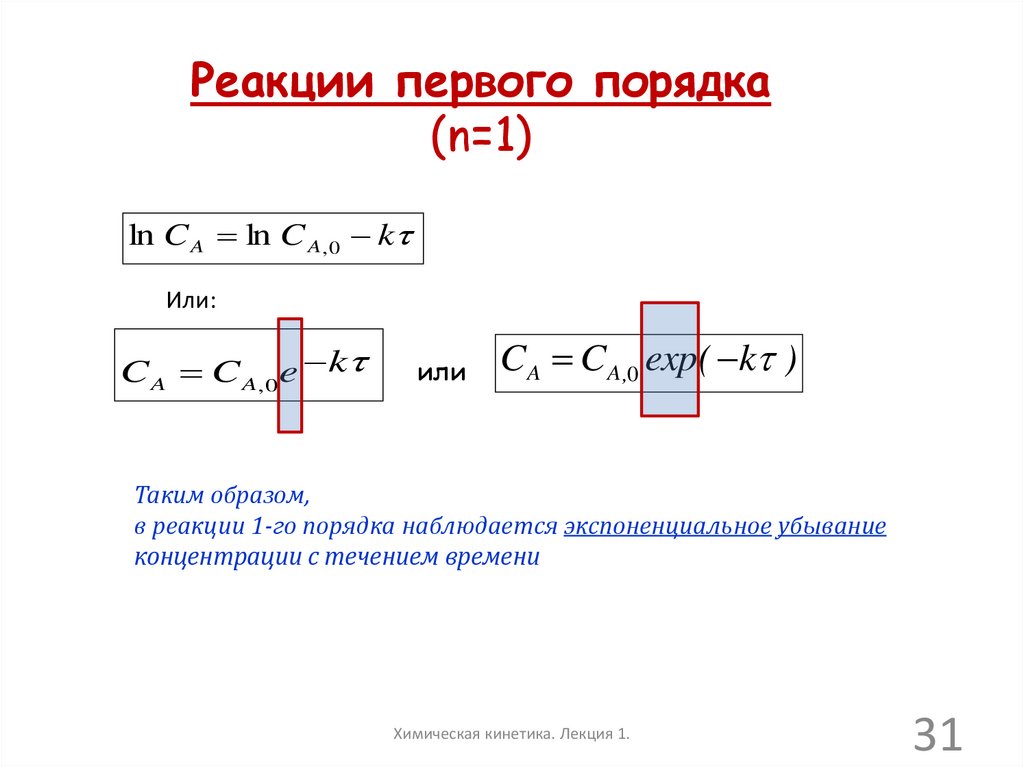
Реакции первого порядка
(n=1)
ln C A ln C A , 0 k
Или:
C A C A, 0 e k
или
CA CA ,0 exp( k )
Таким образом,
в реакции 1-го порядка наблюдается экспоненциальное убывание
концентрации с течением времени
Химическая кинетика. Лекция 1.
31

32.

Реакции первого порядка
(n=1)
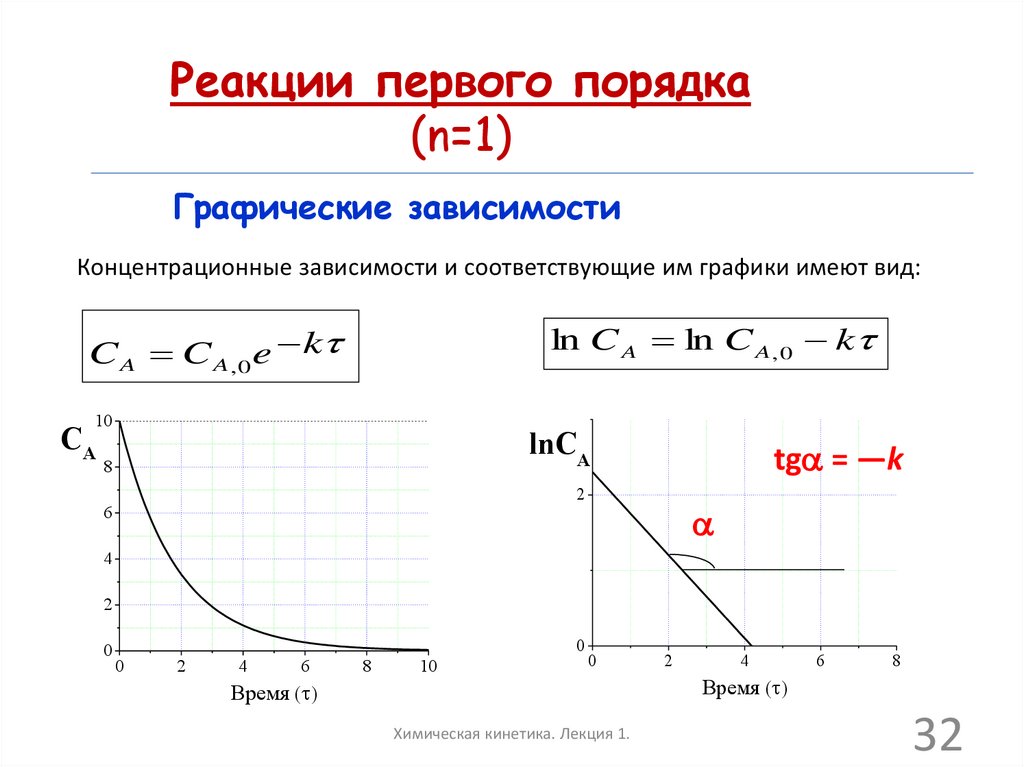
Графические зависимости
Концентрационные зависимости и соответствующие им графики имеют вид:
ln C A ln C A , 0 k
C A C A, 0 e k
10
CA
lnCA
8
tga = —k
2
6
a
4
2
0
0
0
2
4
6
8
10
0
Время ( )
Химическая кинетика. Лекция 1.
2
4
6
8
Время ( )
32

33.

Реакции первого порядка
(n=1)
Период полупревращения
C A ,0
Если τ = τ1/2 /, то C A
2
тогда
ln
C A ,0
ln C A ,0 k 1 / 2
2
ln 2
Откуда:
τ1 / 2
k
Таким образом, для реакции первого
порядка время полупревращения
не зависит от начальной
концентрации, а определяется
только константой скорости реакции
Химическая кинетика. Лекция 1.
33

34.

Реакции первого порядка
(n=1)
10
CA
8
6
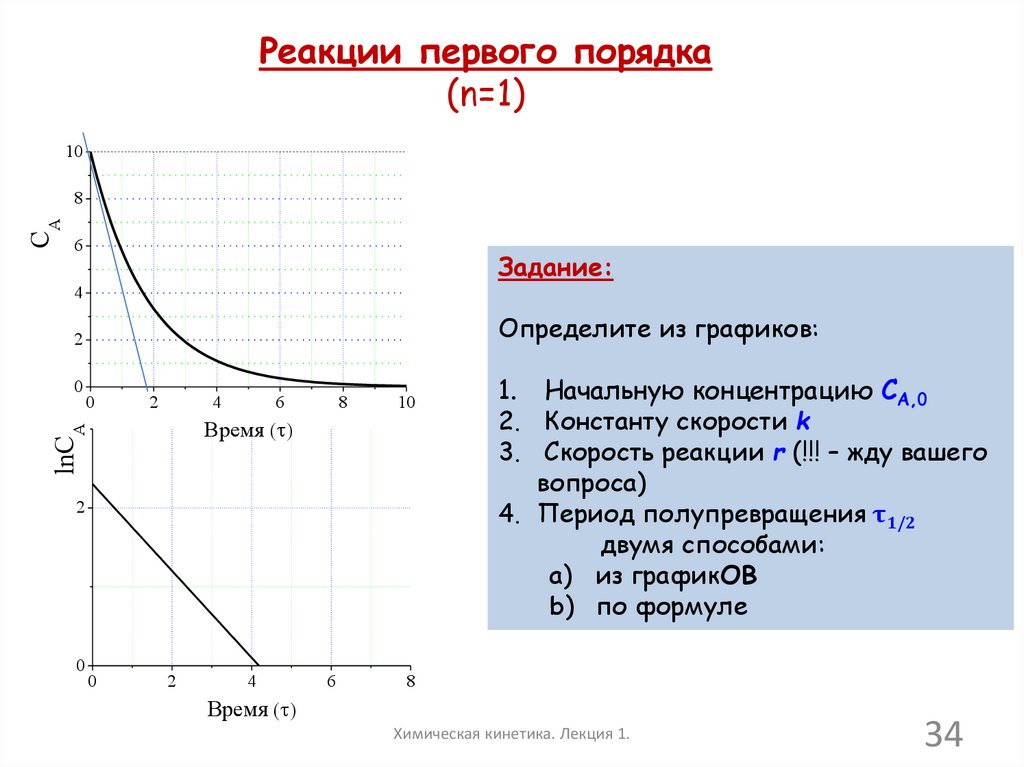
Задание:
4
Определите из графиков:
2
0
2
4
6
8
10
Время ( )
lnCA
0
2
0
0
2
4
6
1. Начальную концентрацию CA,0
2. Константу скорости k
3. Скорость реакции r (!!! – жду вашего
вопроса)
4. Период полупревращения τ1/2
двумя способами:
a) из графикОВ
b) по формуле
8
Время ( )
Химическая кинетика. Лекция 1.
34

35.

Реакции второго порядка
(n=2)
Теперь рассмотрим реакцию первого порядка.
k
A продукты...
По закону действующих масс:
k
2 A продукты...
k
A B продукты...
r kCAn A
С учетом условия нулевого порядка nA= 2: r kCA2
Итак,
r kCA2
r kC1ACB1
Скорость реакции 1-го порядка прямо пропорциональна квадрату концентрации.
Согласно определению скорости реакции:
Объединив формулы:
r
dC A
kCA2
d
dCA
d
Это кинетическое уравнение для реакции второго порядка в
дифференциальной форме
Химическая кинетика. Лекция 1.
35

36.

Реакции второго порядка
(n=2)
dC A
kCA2
d
Разделим переменные и проинтегрируем:
CA
dC A
k d
2
CA
C A, 0
0
Получаем зависимость концентрации исходного реагента от времени:
1
1
k
CA
C A, 0
или
CA
Химическая кинетика. Лекция 1.
1
1
k
C A, 0
36

37.

Реакции второго порядка
(n=2)
CA
1
1
k
C A, 0
1
1
k
CA
C A, 0
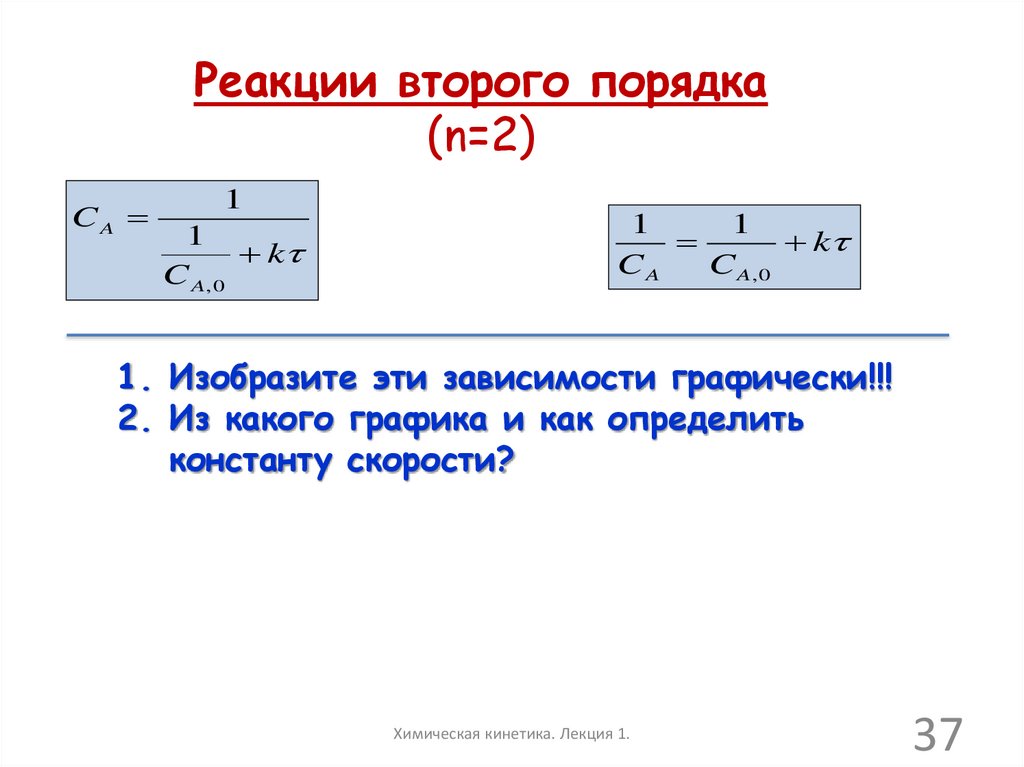
1. Изобразите эти зависимости графически!!!
2. Из какого графика и как определить
константу скорости?
Химическая кинетика. Лекция 1.
37

38.

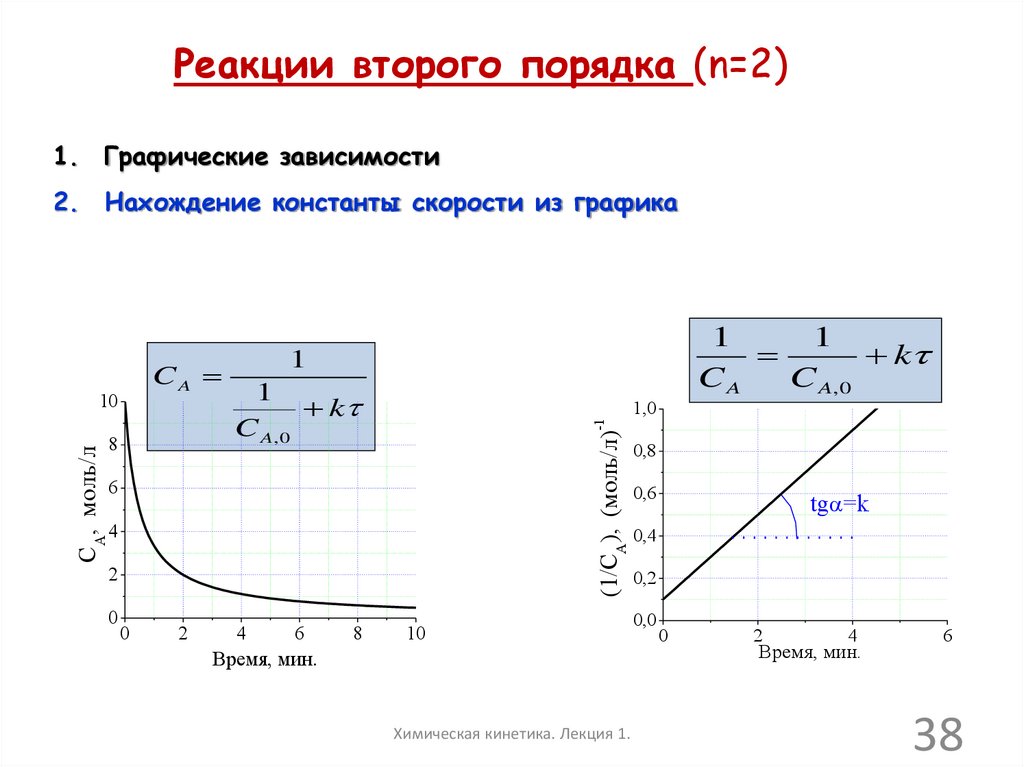
Реакции второго порядка (n=2)
1. Графические зависимости
2. Нахождение константы скорости из графика
CA, моль/л
8
1
k
C A, 0
1,0
-1
10
1
(1/CA), (моль/л)
CA
1
1
k
CA
C A, 0
6
4
2
0
0
2
4
6
8
10
Время, мин.
Химическая кинетика. Лекция 1.
0,8
0,6
tga=k
0,4
0,2
0,0
0
2
4
Время, мин.
6
38

39.

Реакции второго порядка (n=2)
Получим формулу для τ1/2
1
1
k
CA
C A, 0
1
1
C A ,0
2
1
k 1 / 2
C A ,0
1
1/ 2
kCA, 0
Таким образом, для реакции 2-го порядка
время полупревращения
обратно пропорционально начальной
концентрации
Химическая кинетика. Лекция 1.
39

40.

Реакции второго порядка
(n=2)
Для реакции:
k
A B продукты...
при СА,0≠ СB,0:
dC A
kCAC B
d
k
C C
1
Ln( A B , 0 )
(C A, 0 C B , 0 )
C A, 0 C B
Химическая кинетика. Лекция 1.
40

41.

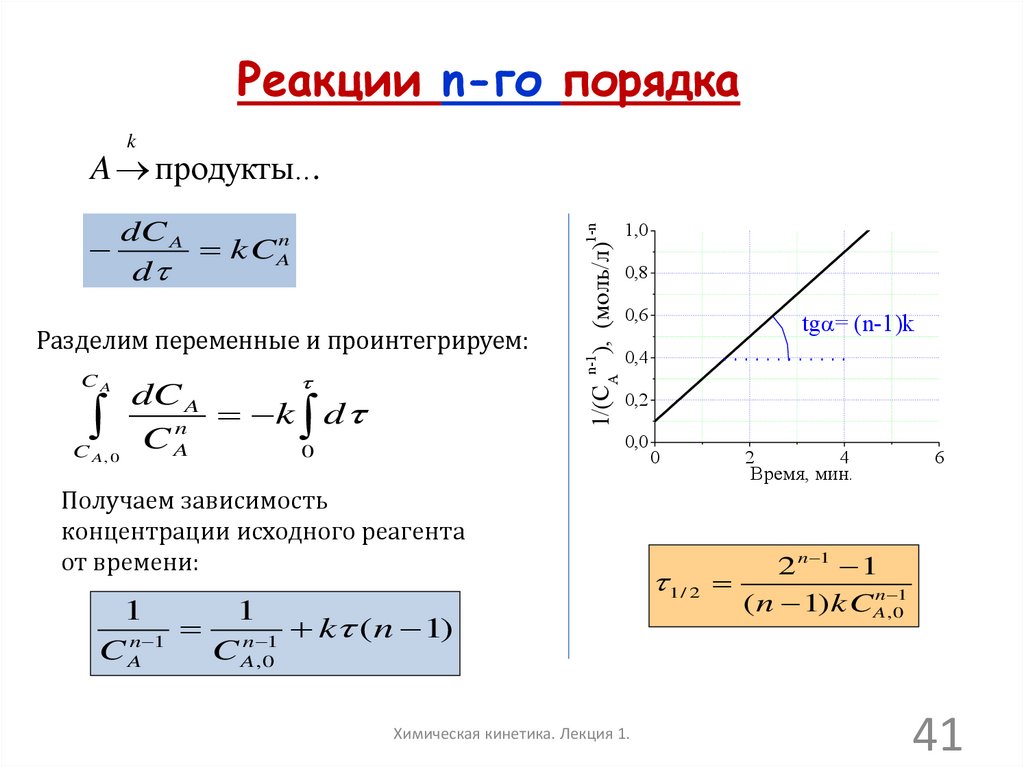
Реакции n-го порядка
k
A продукты...
CA
dC A
k d
n
CA
C A, 0
0
n-1
Разделим переменные и проинтегрируем:
1/(CA ), (моль/л)
1-n
dC A
kCAn
d
1,0
0,8
0,6
tga= (n-1)k
0,4
0,2
0,0
Получаем зависимость
концентрации исходного реагента
от времени:
1
1
k (n 1)
n 1
n 1
CA
C A, 0
Химическая кинетика. Лекция 1.
0
2
4
Время, мин.
6
2 n 1 1
1/ 2
( n 1) kCAn , 01
41

42.

Подходы и методы определения порядка
реакции
!!! Порядки реакций определяются на основе экспериментальных данных!!!
1. Нахождение общего порядка реакции
k
2 A B продукты.. .
Смешаем компоненты в стехиометрическом соотношении, т.е. СА,0=2С0, СВ,0=С0
dC
k ( 2C ) n A C nB
d
(в любой момент времени)
dC
( k 2 n A )C n A nB
d
Обозначим: k * k 2 n A , nA+nB=n –общий порядок
Тогда
dC
k *C n
d
Из опытов определяют общий порядок n
Химическая кинетика. Лекция 1.
42

43.

Подходы и методы определения порядка реакции
2.
Нахождение порядка реакции по компоненту
(метод избыточных компонентов,
или метод изолирования Оствальда)
k
A B продукты...
Смешаем компоненты в соотношении СА,0>>СВ,0, т.е. А возьмем в избытке. Тогда:
dC
kC n A C nB ( kC n A )C nB
d
Обозначим:
Тогда
k * kCA A const
n
dC
n
k *C B B
d
Из опытов определяют частный порядок nВ.
Затем выполняют опыт при СА,0<<СВ,0, и определяют nА
Химическая кинетика. Лекция 1.
43

44.

Подходы и методы определения порядка
реакции
3. Графический метод
Только одна из зависимостей будет линейный вид, по виду
которой можно установить порядок реакции
Порядок
C(τ)
Линейная форма
n=0
C A C A , 0 k
C A C A , 0 k
С=f(τ)
n=1
C A C A, 0 e k
ln C A ln C A , 0 k
LnC=f(τ)
n=2
C A 1 /(
n=3
C A2 1 /(
1
k )
C A, 0
1
1
k
CA
C A, 0
1
2k )
C A2 , 0
1
1
2k
C A2
C A2 , 0
Химическая кинетика. Лекция 1.
1
f ( )
C 1A
1
f ( )
C A2
44

45.

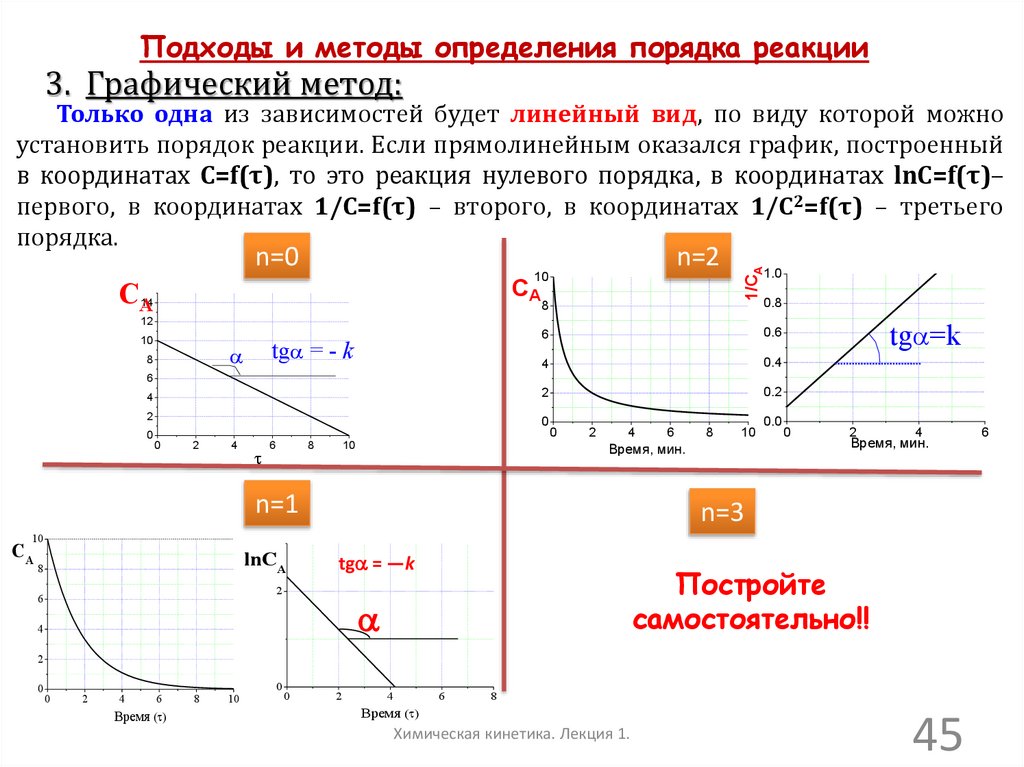
Подходы и методы определения порядка реакции
3. Графический метод:
Только одна из зависимостей будет линейный вид, по виду которой можно
установить порядок реакции. Если прямолинейным оказался график, построенный
в координатах C=f(τ), то это реакция нулевого порядка, в координатах lnC=f(τ)–
первого, в координатах 1/C=f(τ) – второго, в координатах 1/C2=f(τ) – третьего
порядка.
n=2
10
CA
CA
14
1/CA
n=0
1.0
0.8
8
12
6
0.6
4
0.4
4
2
0.2
2
0
10
tga = - k
a
8
tga=k
6
0
0
2
4
6
8
10
0
2
4
6
8
10
Время, мин.
n=1
0.0
0
2
4
Время, мин.
n=3
10
CA
lnCA
8
tga = —k
2
6
Постройте
самостоятельно!!
a
4
2
0
0
0
2
4
6
Время ( )
8
10
0
2
4
6
8
Время ( )
Химическая кинетика. Лекция 1.
45
6

46.

Подходы и методы определения порядка
реакции
4. Подбор кинетического уравнения для константы скорости
Из расчета только по одной из формул для различных моментов
времени τ, величина k будет оставаться постоянной (константой), откуда
следует сделать вывод о порядке реакции
Порядок
n=0
n=1
Формула расчета k
k
k
k
n=2
k
n=3
Химическая кинетика. Лекция 1.
1
1
1
(C A, 0 C A )
ln
(
C A,0
CA
1
1
)
CA
C A, 0
1
1
1
( 2 2 )
2 C A
C A, 0
46

47.

Подходы и методы определения порядка
реакции
5. По периоду полупревращения
(a) Определяют τ1/2 при различных начальных концентрациях СА,0. По
характеру зависимости τ1/2 от СА,0 делают вывод о порядке реакции (см.
таблицу)
Порядок
n=0
n=1
n=2
n=3
Формула τ1/2
1/ 2
C A,0
2k
ln 2
2k
1
1/ 2
kCA, 0
3
1/ 2
2kCA2 , 0
1/ 2
Химическая кинетика. Лекция 1.
τ1/2 от СА,0
τ1/2 СА,0
τ1/2 ≠ f(СА,0)
τ1/2 1/СА,0
τ1/2 1/С2А,0
47

48.

Подходы и методы определения порядка
реакции
5. По периоду полупревращения
(б) Метод Оствальда – Нойеса.
Определяют τ1/2 при двух различных начальных концентрациях СА,0(1) и
СА,0(2).
Далее по формуле вычисляют порядок реакции:
(1)
Ln 1/ 2
1 / 2 ( 2 )
n 1
C A , 0 ( 2)
Ln
C
(
1
)
A, 0
Химическая кинетика. Лекция 1.
48

49.

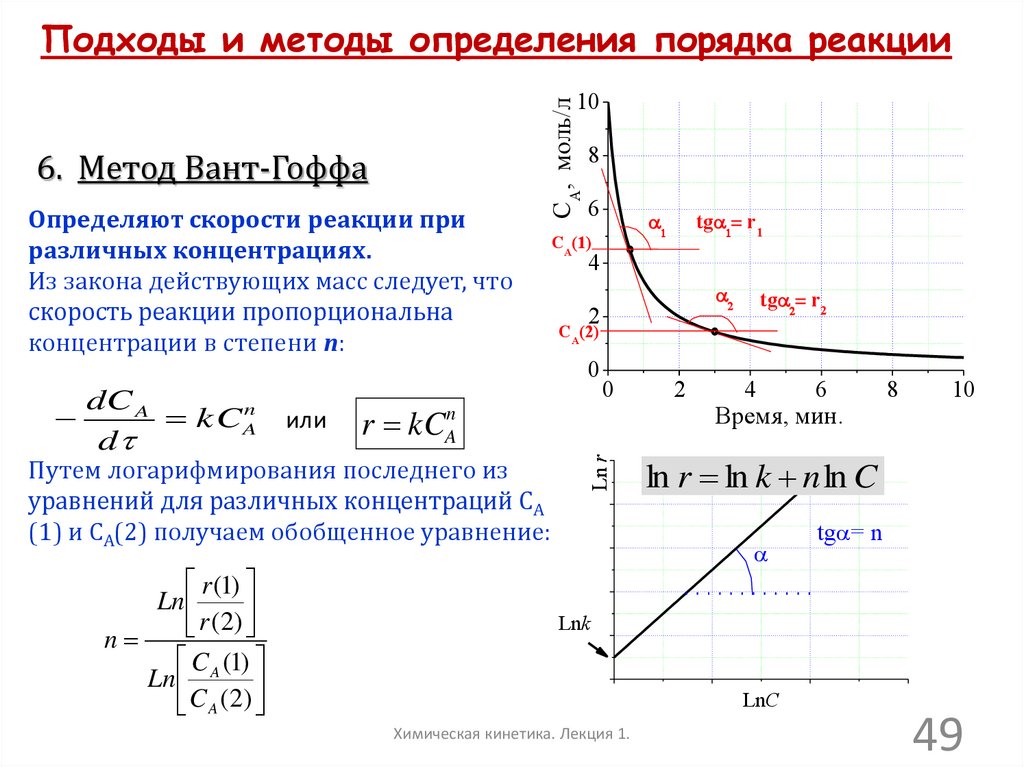
Подходы и методы определения порядка реакции
6. Метод Вант-Гоффа
Определяют скорости реакции при
различных концентрациях.
Из закона действующих масс следует, что
скорость реакции пропорциональна
концентрации в степени n:
или
6
tga r1
a
CA(1)
4
a
2
tga r2
CA(2)
0
r kCAn
Путем логарифмирования последнего из
уравнений для различных концентраций СА
(1) и СА(2) получаем обобщенное уравнение:
r (1)
Ln
r (2)
n
C (1)
Ln A
C A ( 2)
8
0
Ln r
dC A
kCAn
d
CA, моль/л
10
2
4
6
Время, мин.
8
10
ln r ln k n ln C
a
tga= n
Lnk
LnC
Химическая кинетика. Лекция 1.
49

50.

Влияние температуры на скорость
(константу скорости) химической реакции
1) Правило Вант-Гоффа:
«При повышении температуры на каждые 10о константа
скорости реакции увеличивается в 2-4 раза»
Коэффициент Вант-Гоффа:
Откуда:
kT 2 kT 1
kT 10
kT
T2 T1
10
Следует иметь в виду, что правило Вант-Гоффа – приближенное,
хотя и очень полезное для оценочных целей.
Химическая кинетика. Лекция 1.
50

51.

Влияние температуры на скорость
(константу скорости) химической реакции
2) Уравнение Аррениуса
(Сванте Август Аррениус, шведский физико-химик, 1859-1927)
Аррениус:
«Не всякое столкновение частиц приводит к химическому
взаимодействию.
Необходимо, чтобы сталкивающиеся молекулы обладали запасом
энергии, называемым энергией активации» химической реакции
Энергия активации – минимальная энергия (избыточная над
средней энергией), которой должны обладать молекулы,
чтобы их столкновение могло привести к к химическому
взаимодействию
Химическая кинетика. Лекция 1.
51

52.

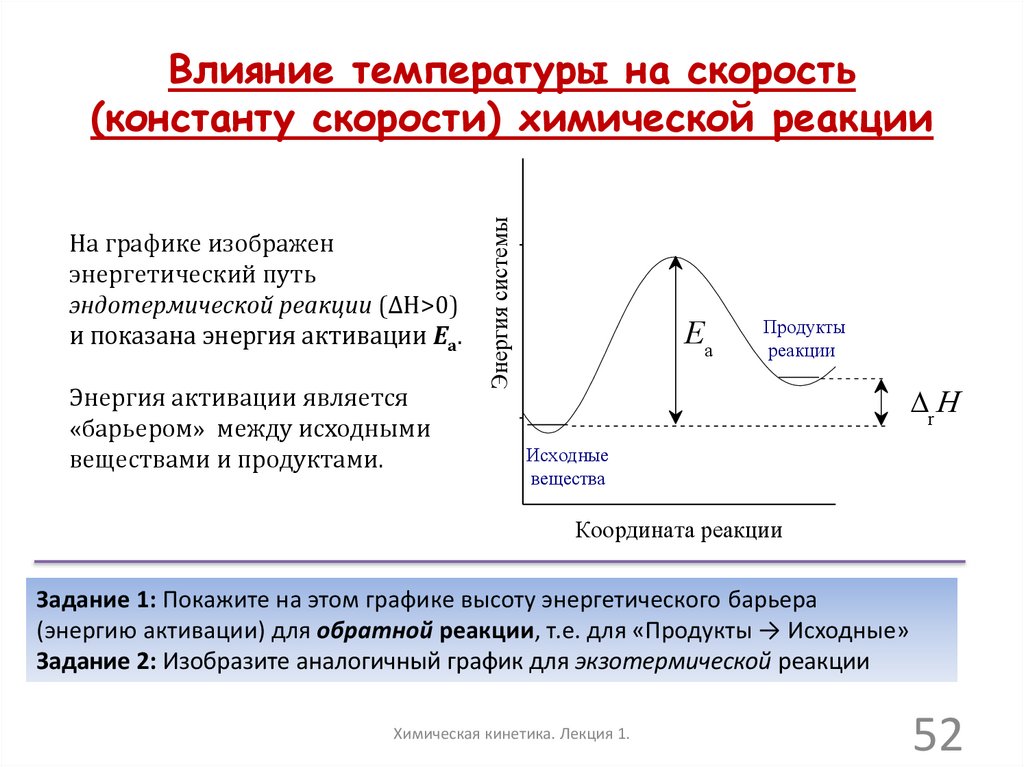
На графике изображен
энергетический путь
эндотермической реакции (∆Н>0)
и показана энергия активации Еа.
Энергия активации является
«барьером» между исходными
веществами и продуктами.
Энергия системы
Влияние температуры на скорость
(константу скорости) химической реакции
Ea
Продукты
реакции
r
Исходные
вещества
Координата реакции
Задание 1: Покажите на этом графике высоту энергетического барьера
(энергию активации) для обратной реакции, т.е. для «Продукты → Исходные»
Задание 2: Изобразите аналогичный график для экзотермической реакции
Химическая кинетика. Лекция 1.
52

53.

Влияние температуры на скорость
(константу скорости) химической реакции
Уравнение Аррениуса
Уравнение Аррениуса - это зависимость константы скорости реакции от
температуры:
где А – коэффициент Аррениуса
(предэкспоненциальный множитель)
k увеличивается с ростом температуры Т
и
уменьшается с ростом энергии активации Еа,
т.е:
k при Т и при Еа
Энергия системы
k Ae
Ea
RT
Ea
Продукты
реакции
r
Исходные
вещества
Координата реакции
Химическая кинетика. Лекция 1.
53

54.

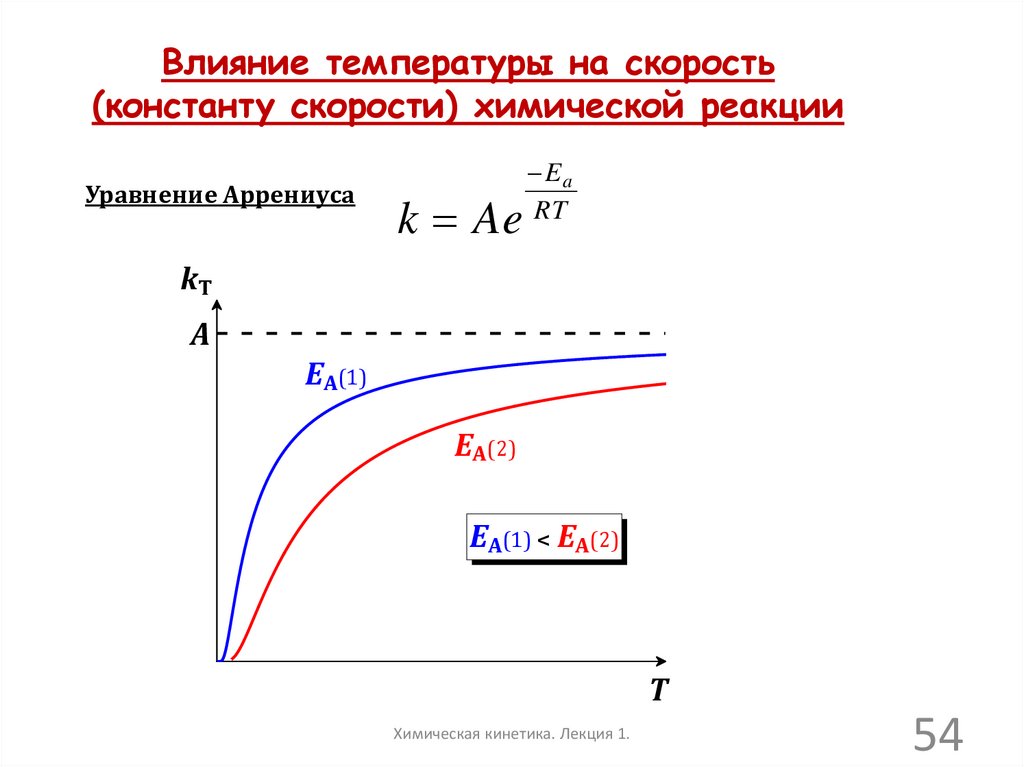
Влияние температуры на скорость
(константу скорости) химической реакции
Уравнение Аррениуса
k Ae
Ea
RT
kT
A
EA(1)
EA(2)
EA(1) < EA(2)
T
Химическая кинетика. Лекция 1.
54

55.

Влияние температуры на скорость
(константу скорости) химической реакции
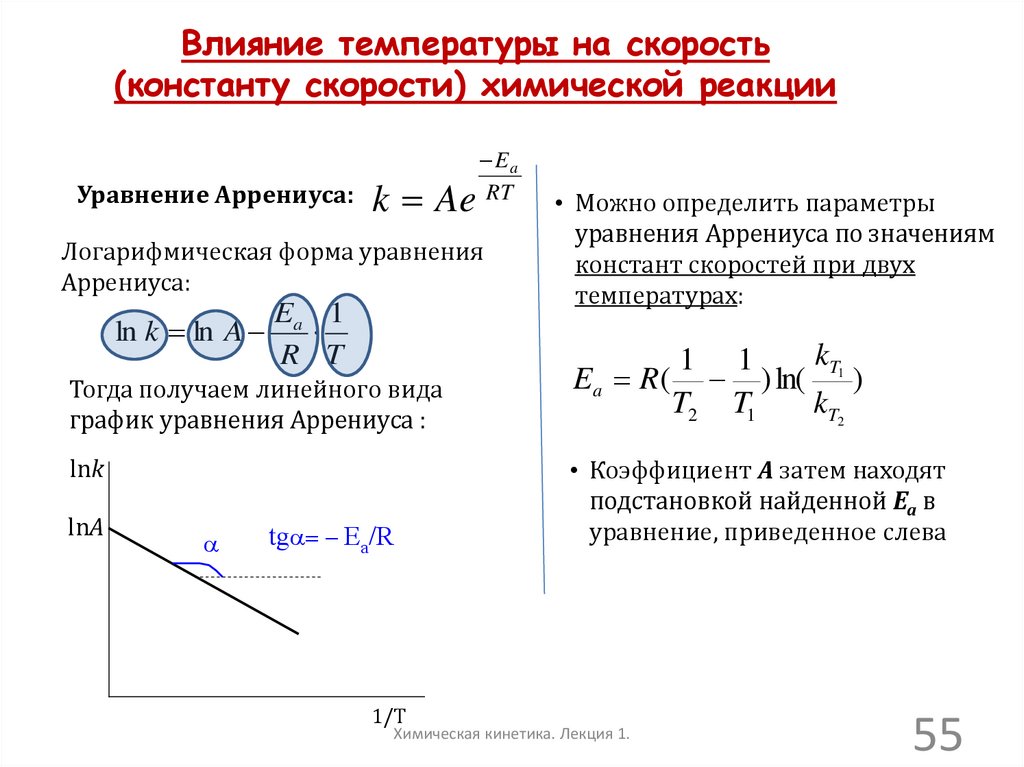
Уравнение Аррениуса:
k Ae
Ea
RT
Логарифмическая форма уравнения
Аррениуса:
Ea 1
ln k ln A
R T
Тогда получаем линейного вида
график уравнения Аррениуса :
lnk
lnA
a
tga Ea/R
1/T
• Можно определить параметры
уравнения Аррениуса по значениям
констант скоростей при двух
температурах:
kT1
1 1
Ea R ( ) ln( )
T2 T1
kT2
• Коэффициент А затем находят
подстановкой найденной Еа в
уравнение, приведенное слева
Химическая кинетика. Лекция 1.
55

56.

Кинетика сложных реакций
До этого мы рассматривали реакции , считая их элементарными,
т.е.протекающими в одну стадию.
Сложными называют реакции, протекающие более, чем в одну стадию.
Пример сложной реакции:
2HI + H2O2 I2 +2H2O
2
1
По формальному признаку это реакция3-го порядка: r kCHI CH 2O2
Но на самом деле это реакция 2-го порядка.
Механизм реакции был выяснен из опыта: реакция протекает в две
последовательные стадии:
(1) HI + H2O2 НIO+H2O
(2) HIO + HI I2 + H2O
При этом скорости стадий: r(1)>>r(2), следовательно, общая скорость реакции
определяется скоростью r(2) более медленной стадии (её называют
скорость определяющая, или лимитирующая стадия).
Химическая кинетика. Лекция 1.
56

57.

Кинетика сложных реакций
Принцип независимости протекания химической реакции:
Если в системе имеет место несколько элементарных реакций, то
каждая из них протекает по тем же законам и с той же скоростью, как и
в отсутствие других реакций при тех же концентрации и температуре
Самыми простыми из сложных реакций являются:
Обратимые
А В
Параллельные A
B
C
Последовательные А В С
Химическая кинетика. Лекция 1.
57

58.

Кинетика сложных реакций
Обратимые (двусторонние) реакции:
А В
k2
r r1 r2
r
При =0
При =
k1
r1 – скорость прямой реакции,
r2 – скорость обратной реакции
dC A
k1C A k 2CB
d
А
В
СА,0
СВ,0
СА,0− x
СВ,0+x
где x – количество вещества А, прореагировавшего к моменту времени
dC A
dx
k1 (C A, 0 x) k 2 (C B , 0 x)
d
d
Решая дифференциальное уравнение и с учетом того, что реакционная
система придет к равновесию, получим:
1
(k1 k 2 ) ln
x
x x
где x − равновесная убыль вещества А
Химическая кинетика. Лекция 1.
58

59.

Кинетика сложных реакций
Обратимые (двусторонние) реакции:
k1
А В
k2
При равновесии скорости прямой и обратной реакций равны ( r1 r2 ).
С учетом этого получим еще одно уравнение:
k1 C B , 0 x
k 2 C A, 0 x
или
k1
KC
k2
где КС – константа равновесия реакции
Таким образом, получаем систему двух уравнений с двум неизвестными:
1
x
(k1 k 2 ) ln
x x
k1
KC
k2
KC
Химическая кинетика. Лекция 1.
C B k1
C A k2
59

60.

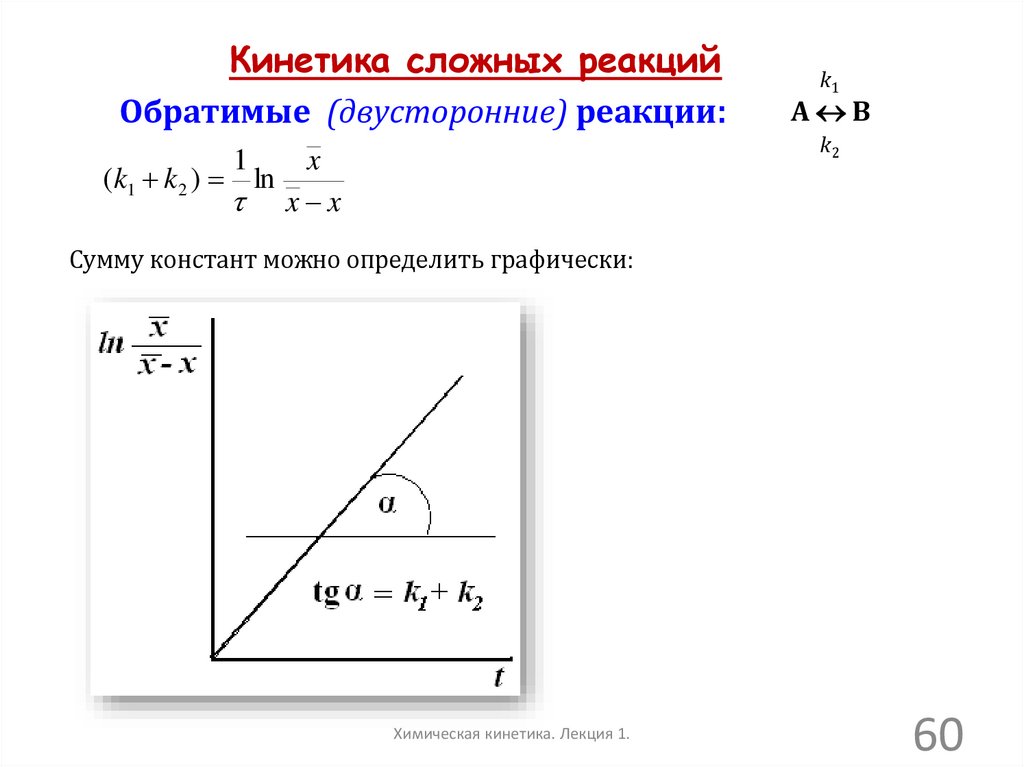
Кинетика сложных реакций
Обратимые (двусторонние) реакции:
1
(k1 k 2 ) ln
k1
А В
k2
x
x x
Сумму констант можно определить графически:
Химическая кинетика. Лекция 1.
60

61.

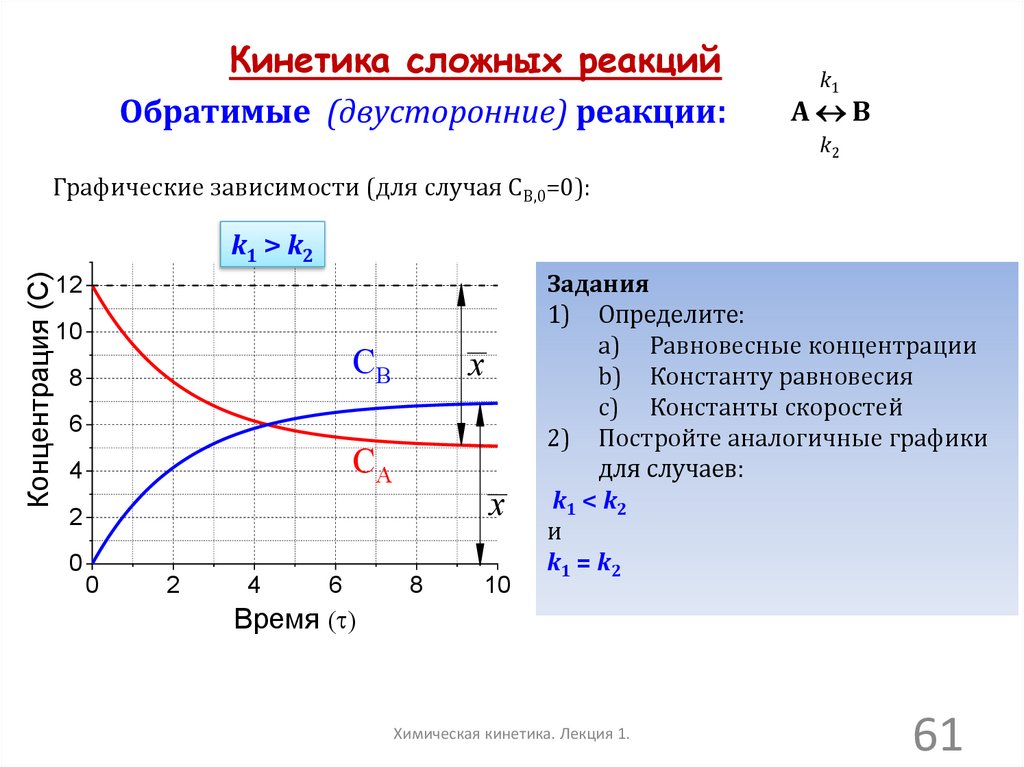
Кинетика сложных реакций
Обратимые (двусторонние) реакции:
k1
А В
k2
Графические зависимости (для случая СВ,0=0):
Концентрация (C)
k1 > k2
12
10
CB
8
x
6
CA
4
x
2
0
0
2
4
6
8
10
Задания
1) Определите:
a) Равновесные концентрации
b) Константу равновесия
c) Константы скоростей
2) Постройте аналогичные графики
для случаев:
k1 < k2
и
k1 = k2
Время ( )
Химическая кинетика. Лекция 1.
61

62.

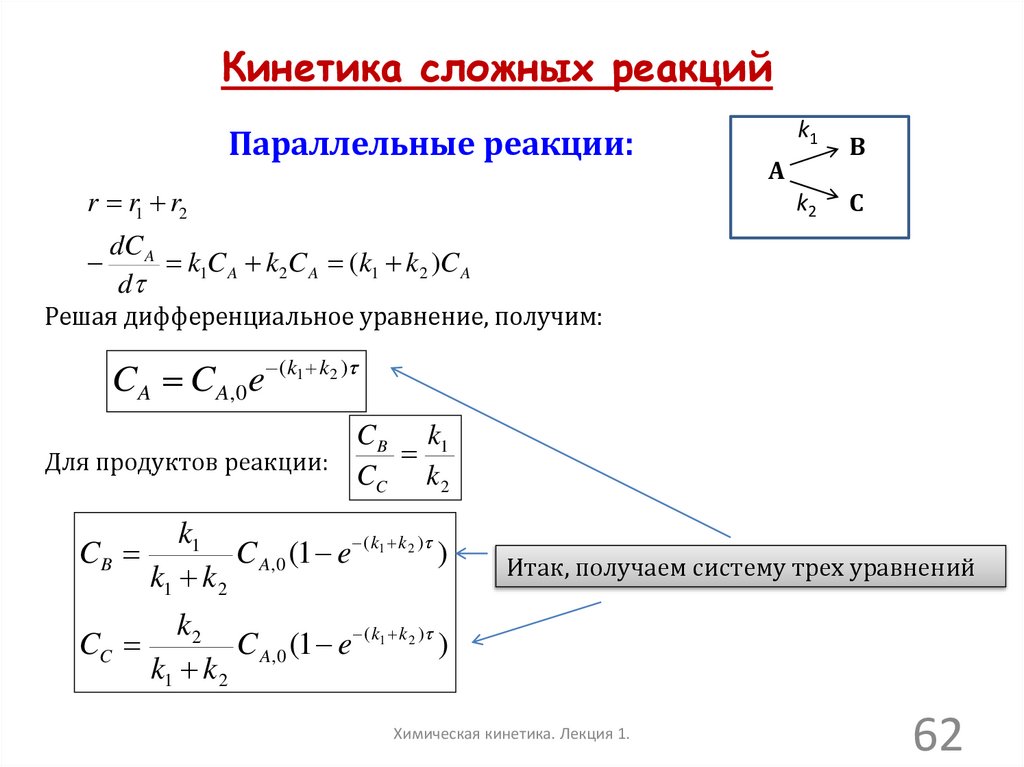
Кинетика сложных реакций
Параллельные реакции:
r r1 r2
k1
B
k2
C
A
dC A
k1C A k 2C A (k1 k 2 )C A
d
Решая дифференциальное уравнение, получим:
C A C A,0e ( k1 k2 )
C B k1
Для продуктов реакции:
CC k 2
CB
k1
C A,0 (1 e ( k1 k2 ) )
k1 k2
CC
k2
C A,0 (1 e ( k1 k2 ) )
k1 k 2
Итак, получаем систему трех уравнений
Химическая кинетика. Лекция 1.
62

63.

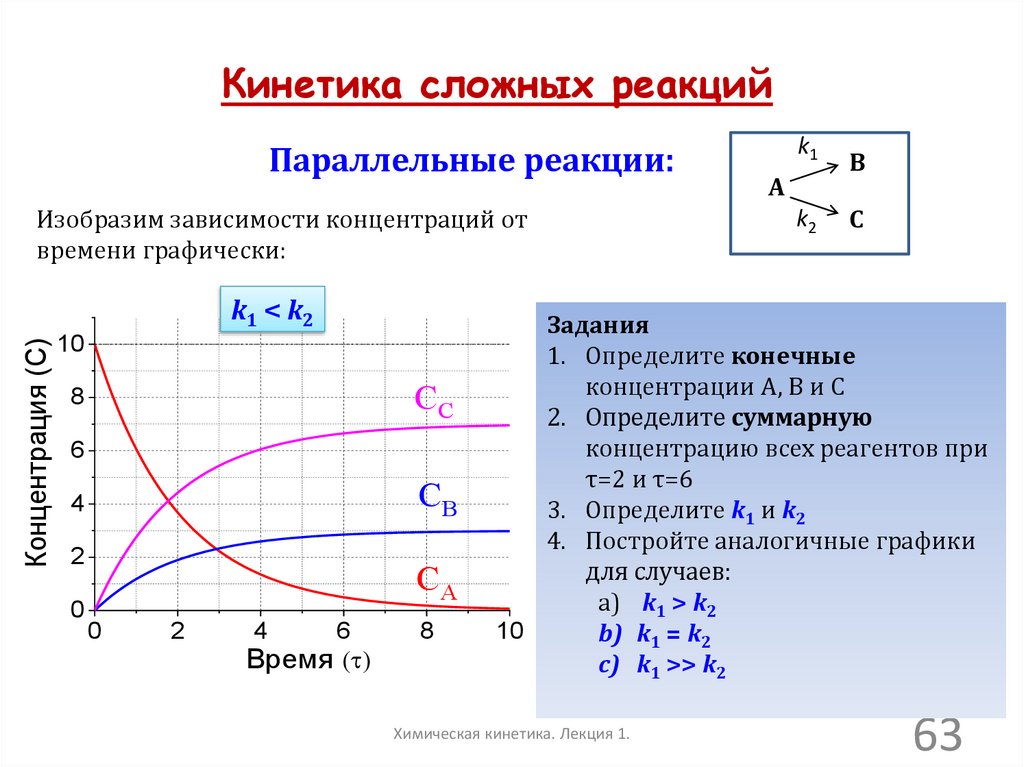
Кинетика сложных реакций
Параллельные реакции:
Изобразим зависимости концентраций от
времени графически:
Концентрация (C)
k1 < k2
10
CC
8
6
CB
4
2
0
CA
0
2
4
6
Время ( )
8
k1
B
k2
C
A
Задания
1. Определите конечные
концентрации А, В и С
2. Определите суммарную
концентрацию всех реагентов при
τ=2 и τ=6
3. Определите k1 и k2
4. Постройте аналогичные графики
для случаев:
a) k1 > k2
10
b) k1 = k2
c) k1 >> k2
Химическая кинетика. Лекция 1.
63

64.

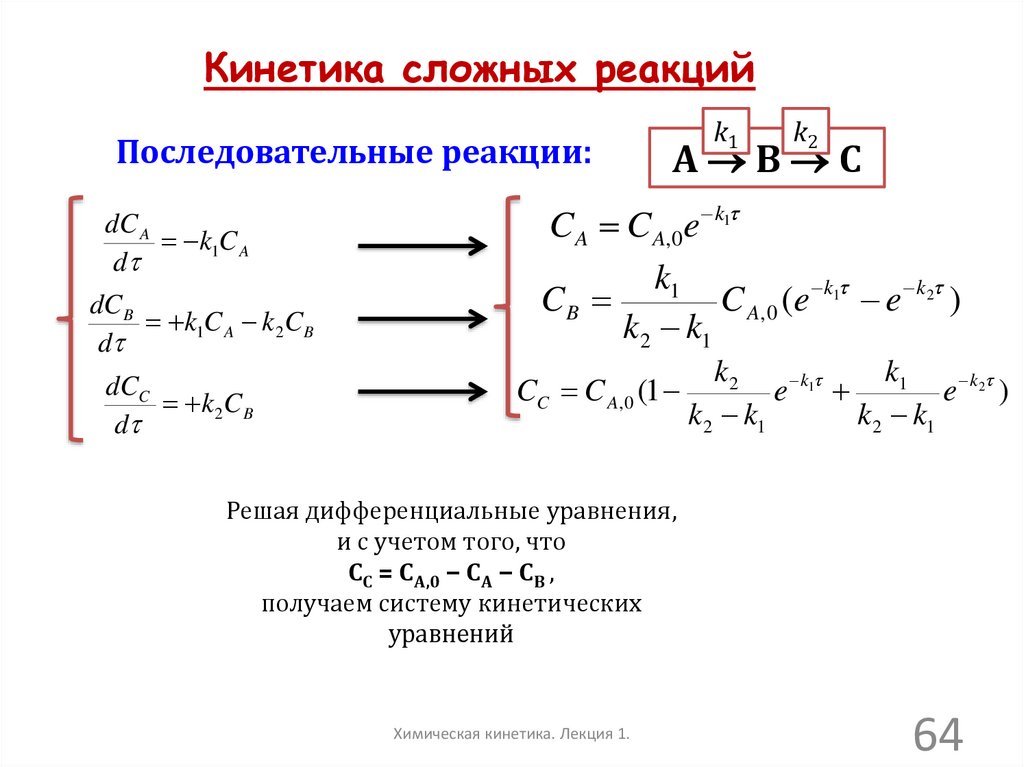
Кинетика сложных реакций
Последовательные реакции:
dC A
k1C A
d
dC B
k1C A k 2C B
d
dCC
k 2C B
d
k1
k2
А В С
C A C A,0e k1
k1
CB
C A, 0 (e k1 e k2 )
k 2 k1
CC C A, 0 (1
k2
k1
e k1
e k2 )
k 2 k1
k 2 k1
Решая дифференциальные уравнения,
и с учетом того, что
СС = СА,0 − СА − СВ ,
получаем систему кинетических
уравнений
Химическая кинетика. Лекция 1.
64

65.

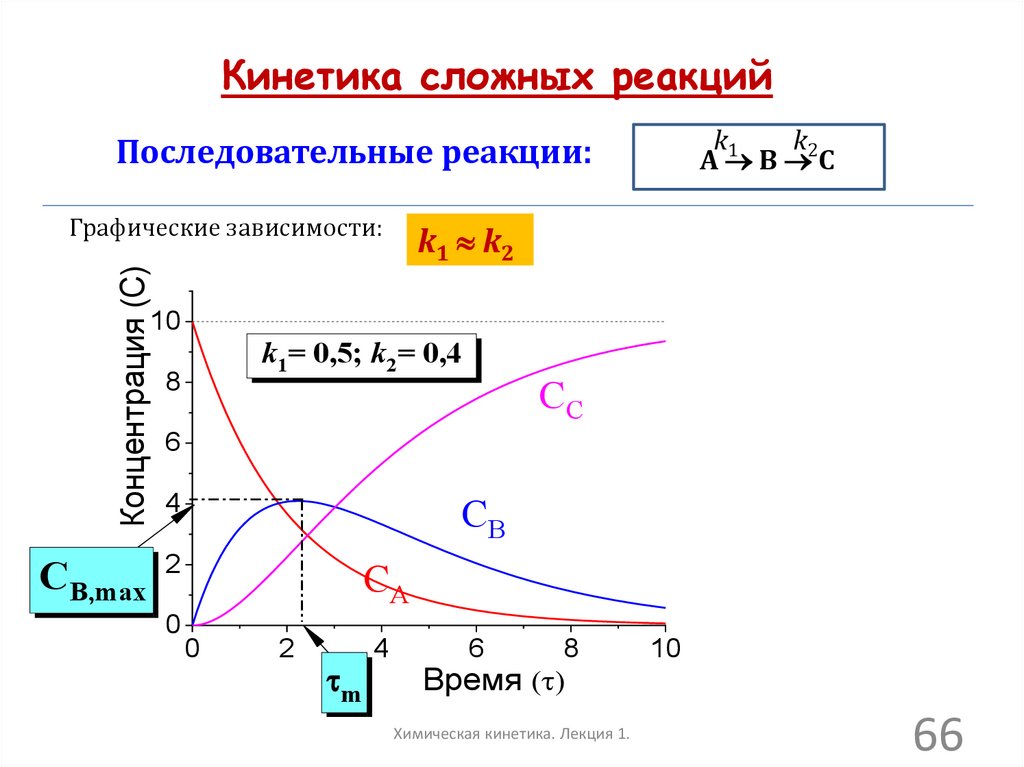
Кинетика сложных реакций
Последовательные реакции:
k1
k2
А В С
1. Поскольку вещество В участвует в двух реакциях (образование и
последующее расходование), зависимость СВ от проходит через
максимум.
dC B
0,
Координаты этого максимума находят из условия экстремума:
d
откуда следует:
CB, max C A,0
k2
)
k1
m
k 2 k1
ln(
1
1
,
где
k2
k1
, где m – время достижения максимальной концентрации СB, max
2. Следует отметить, что график СС от имеет S-образную форму!
Точка перегиба соответствует по времени m
Химическая кинетика. Лекция 1.
65

66.

Кинетика сложных реакций
k1
k
А
В 2С
Последовательные реакции:
Концентрация (C)
Графические зависимости:
k1 k2
10
k1= 0,5; k2= 0,4
8
CC
6
CB
4
CB,max 2
0
CA
0
2
m
4
6
8
Время ( )
Химическая кинетика. Лекция 1.
10
66

67.

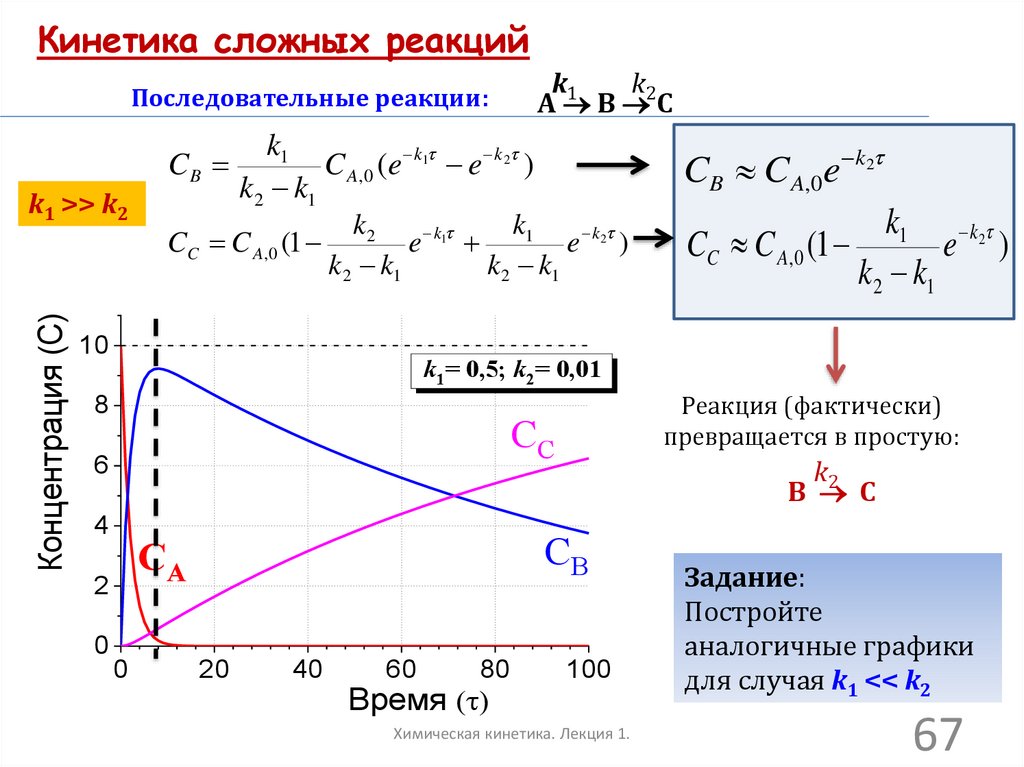
Кинетика сложных реакций
k1
k2
А В С
Последовательные реакции:
CB
Концентрация (C)
k1 >> k2
k1
C A, 0 (e k1 e k2 )
k 2 k1
CC C A, 0 (1
k2
k1
e k1
e k2 )
k 2 k1
k 2 k1
10
k1 k2
CC C A,0 (1
e )
k2 k1
k1= 0,5; k2= 0,01
8
Реакция (фактически)
превращается в простую:
CC
6
4
0
k2
В С
CB
CA
2
0
CB C A,0e k2
20
40
60
80
Время ( )
100
Химическая кинетика. Лекция 1.
Задание:
Постройте
аналогичные графики
для случая k1 << k2
67

68.

Кинетика сложных реакций
Метод квазистационарных концентраций Боденштейна
Макс Боденштейн (1871-1942) Max Ernst August Bodenstein; немецкий
химик и физик, известный по своим работам в области химической
кинетики. Он был первым человеком, сформулировавшим идею
существования цепной реакции.
Математическое описание кинетики сложных, многостадийных
процессов, протекающих с образованием нескольких промежуточных веществ,
представляет собой систему дифференциальных уравнений. Для точного
решения таких систем и разработки кинетической модели процесса
необходимо получение экспериментальных зависимостей С=f(τ) для всех
участников процесса. Достаточно часто аналитическое определение ничтожно
малой концентрации реакционноспособного интермедиата (промежуточного
вещества) не представляется возможным.
Если в системе имеются последовательные стадии, и скорости
образования и расходования промежуточных веществ равны, что, например,
наблюдается в реакциях с участием реакционноспособных частиц, то
скорость по промежуточному веществу dCпром еж.
d
0
что позволяет существенно упростить решение системы уравнений, в которой
не содержится концентрация промежуточного
продукта.
Химическая кинетика. Лекция 1.
68

69.

Кинетика сложных реакций
Метод квазистационарных концентраций Боденштейна
Рассмотрим реакцию:
k1
k2
А В С
k3
k4
D
k5
E
Запишем для неё систему дифференциальных уравнений:
dC A
k1C A
d
dC B
k1C A k 2C B k3CC
d
dCC
k 2C B k3CC k 4CC k5CC
d
dC D
k 4 CC
d
dC E
k 5 CC
d
Химическая кинетика. Лекция 1.
69

70.

Кинетика сложных реакций
Метод квазистационарных концентраций Боденштейна
Рассмотрим еще один пример сложной реакции
(в ней появились стехиометрические коэффициенты):
k1
k2
А +D 2В С
k3
dC A
k1C AC D
d
dC B
2(k1C AC D k 2C B2 k3CC )
d
dCC
k 2C B2 k3CC
d
Запишем для неё систему
дифференциальных уравнений:
В данном случае промежуточным веществом является В. И если скорости
образования и расходования для него равны, то скорость по этому веществу
dCВ/d 0.
2
Тогда
0 2(k1C AC D k 2C B k3CC )
Откуда : C B2
k1C AC D k3CC
k2
Подставляем в уравнение для С:
dCC
k C C k3CC
k2 ( 1 A D
) k3CC
d
k2
Химическая кинетика. Лекция 1.
70

71.

Кинетика сложных реакций
Метод квазистационарных концентраций Боденштейна
Приведем еще один пример реакции, включающей обратимую стадию –
реакцию разложения озона: 2О → 3О
k1
3
2
Эта реакция протекает через следующие стадии:
При соблюдении условия:
dC О
0
d
C О
О 3 ↔ О2 + O
k2
k
3
O + О3 →
2О2
k1C О3
k 2C О2 k3C О3
Уравнение для озона:
dCО3
d
k1CО3 k 2CО2 CО k3CО3 CО
После подстановки выражения для СО в кинетическое уравнение скорости
по исходному веществу (О3) и математических преобразований получим:
dCО3
d
Итак:
k1CО3 k2CО2
dCО3
d
k1C О3
k2C О2 k3C О3
2k1k3CО23
k2C О2 k3C О3
k3CО3
k1C О3
k2C О2 k3C О3
2k1k3CО23
k2C О2 k3C О3
В зависимости от соотношения СО2 и СО3
будет наблюдаться либо 1-й, либо 2-й
порядок реакции
Химическая кинетика. Лекция 1.
71

72.

Теория элементарных актов
химической реакции
Элементарным актом (ЭА) называют единичный акт
превращения частиц (атомов, молекул, ионов, ...) исходных
веществ
в
частицы
продуктов,
протекающий
через
единичный энергетический барьер
Химическая кинетика. Лекция 1.
72

73.

Теория элементарных актов химической реакции
I. Теория Аррениуса
Мы её уже кратко рассматривали немного раньше.
1. Для того, чтобы ЭА был возможен,
необходимо, чтобы
взаимодействующие частицы были
возбуждены
2. Взаимодействующие частицы
должны обладать неким
достаточным для ЭА запасом энергии,
т.е. энергией активации химической
реакции (Eа)
Энергия системы
Выделим главные положения этой
теории:
Химическая кинетика. Лекция 1.
A*
k2
k1
k-1
A
Ea
Продукты
реакции
Координата реакции
73

74.

Теория элементарных актов химической реакции
3. ЭА – это двухстадийный процесс:
k1
k2
*
А А продукты
k 1
при этом k1 и k ―1 >> k2, следовательно, 2я стадия лимитирует общую скорость
реакции.
Энергия системы
I. Теория Аррениуса
A*
k2
k1
k-1
A
4. Константа скорости
зависит от Т и ЕА:
всей
k Ae
Ea
Продукты
реакции
реакции
Ea
RT
Координата реакции
Недостатки теории Аррениуса:
1. Для сложных реакций уже уравнение Аррениуса имеет более
сложный вид
2. Еа и А могут зависеть от Т Химическая кинетика. Лекция 1.
74

75.

Теория элементарных актов химической реакции
II. Теория активных соударений (ТАС)
Молекулы должны сблизиться на определенное расстояние (равносильно
столкновению).
Не все соударения приводят к химическому превращению: энергия молекул должна
быть не менее Еа.
Способы активации молекул:
1. Тепловая активация – энергия поступательного движения переходит в энергию
возбуждения
2. Радиационная активация – возбуждение молекул за счет поглощения фотонов
электромагнитного излучения: А + h → A*
3. При взаимодействие с другими частицами – электронами, протонами,…
4. Взаимодействие электрическим полем или разрядом
5. Взаимодействие с катализатором
Основные положения ТАС:
1. При столкновении взаимодействие происходит «мгновенно»
2. Химическая реакция протекает, в основном, за счет двойных соударений
3. В ходе химической реакции распределение Максвелла-Больцмана по энергиям
практически сохраняется, т.е. скорость установления распределения выше
скорости реакции.
Химическая кинетика. Лекция 1.
75

76.

Теория элементарных актов химической реакции
II. Теория активных соударений (ТАС)
Из ТАС получают уравнение для расчета
предэкспоненциального множителя
(коэффициента Аррениуса):
1
2
A
2 8kT
RT
k AB
N
e
A
m
E
1
2
Выражение в круглых скобках и есть коэффициент
2 8kT
A
NA
AB
Аррениуса (предэкспоненциальный множитель) А:
m
_
• Средняя арифметическая скорость движения молекул
8kT
v
m
• Приведенная масса m* сталкивающихся молекул А и В
m
m A mB
m A mB
• Средний эффективный диаметр σАВ молекул А и В
А
В
σАВ
76

77.

Теория элементарных актов химической реакции
II. Теория активных соударений (ТАС)
Обще число столкновений в ед. времени:
(nA и nB – концентрации частиц)
Число активных столкновений z* в ед. времени:
1
2
2 8kT
z AB
m n A nB
z* z e
EA
RT
Рассчитаем общее число столкновений молекул воздуха в 1 секунду:
• в 1 м3
• в 1 см3
Химическая кинетика. Лекция 1.
77

78.

Теория элементарных актов химической реакции
II. Теория активных соударений (ТАС)
Теория
активных
столкновений
дает
возможность
рассчитать
предэкспоненциальные множители для ряда реакций, протекающих в
газовой фазе, но не позволяет теоретически оценить энергию активации и
ее необходимо определять экспериментально.
Для большинства реакций константы скорости, вычисленные по уравнению,
1
значительно превышают опытные значения.
k
A
8kT 2
RT
N
e
A
m
E
2
AB
Это связано с тем, что молекулы представляют собой не
бесструктурные частицы, и для их взаимодействия должно соблюдаться
определенное благоприятное расположение активных групп.
В связи с этим в выражение для константы скорости необходимо ввести
дополнительный стерический
множитель (Р), характеризующий
пространственные затруднения при осуществлении реакции.
Таким образом, уравнение для константы скорости реакции в теории
активных столкновений имеет следующий вид: k = Р z exp(- E/RT)
78

79.

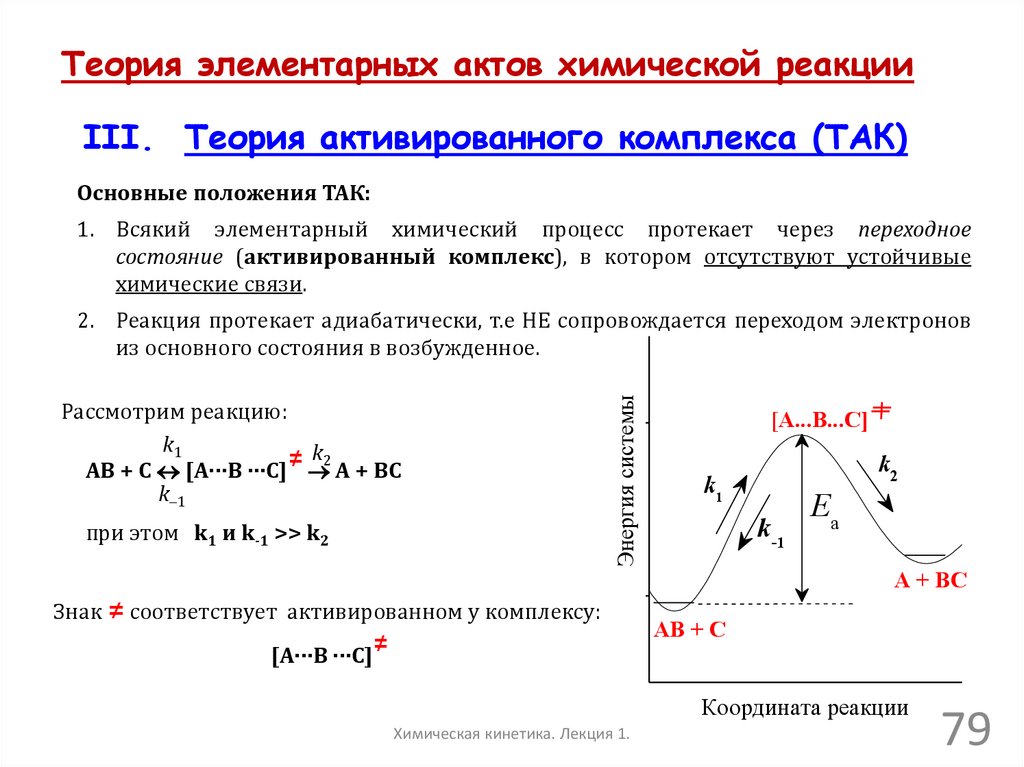
Теория элементарных актов химической реакции
III. Теория активированного комплекса (ТАК)
Основные положения ТАК:
1. Всякий элементарный химический процесс протекает через переходное
состояние (активированный комплекс), в котором отсутствуют устойчивые
химические связи.
Рассмотрим реакцию:
k1
k2
≠
АВ + С [А···B ···C] A + BC
k 1
при этом k1 и k-1 >> k2
Энергия системы
2. Реакция протекает адиабатически, т.е НЕ сопровождается переходом электронов
из основного состояния в возбужденное.
Знак ≠ соответствует активированном у комплексу:
≠
[А···B ···C]
[A...B...C]
k2
k1
k-1
Ea
A + BC
AB + C
Координата реакции
Химическая кинетика. Лекция 1.
79

80.

Теория элементарных актов химической реакции
III. Теория активированного комплекса (ТАК)
k1
≠ k2
АВ + С [А···B ···C] A + BC
k 1
Предполагается, что на стадии образования активированного комплекса
[А …В…С]≠ устанавливается равновесие, характеризуемое константой
равновесия:
Использование аппарата статистической термодинамики позволило
получить следующее выражение для константы скорости бимолекулярной
реакции, протекающей в газовой фазе:
где – трансмиссионный коэффициент, учитывающий долю активированных
комплексов, переходящих в продукты реакции, для большинства реакций =1;
h – постоянная Планка; Pо – стандартное давление; Δν≠ - изменение числа частиц
при образовании активированного комплекса; ΔSo≠ - энтропия активации; ΔНо≠ энтальпия активации; kБ – постоянная
Больцмана.
Химическая кинетика. Лекция 1.
80

81.

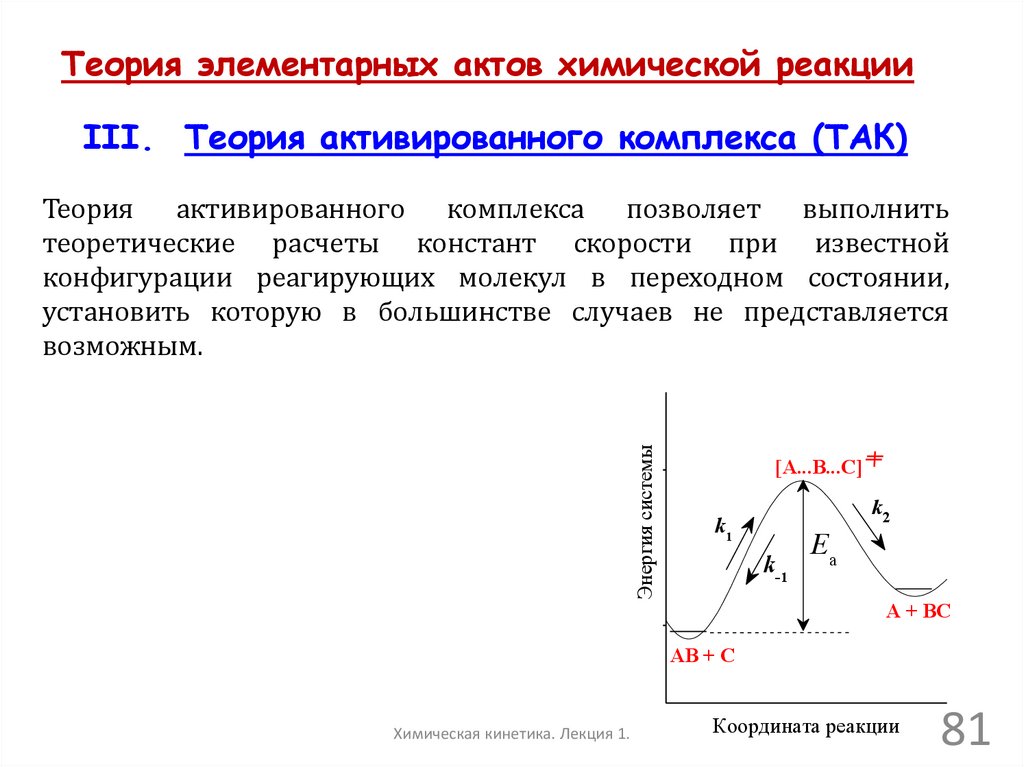
Теория элементарных актов химической реакции
III. Теория активированного комплекса (ТАК)
Энергия системы
Теория активированного комплекса позволяет выполнить
теоретические расчеты констант скорости при известной
конфигурации реагирующих молекул в переходном состоянии,
установить которую в большинстве случаев не представляется
возможным.
[A...B...C]
k2
k1
k-1
Ea
A + BC
AB + C
Химическая кинетика. Лекция 1.
Координата реакции
81

82.

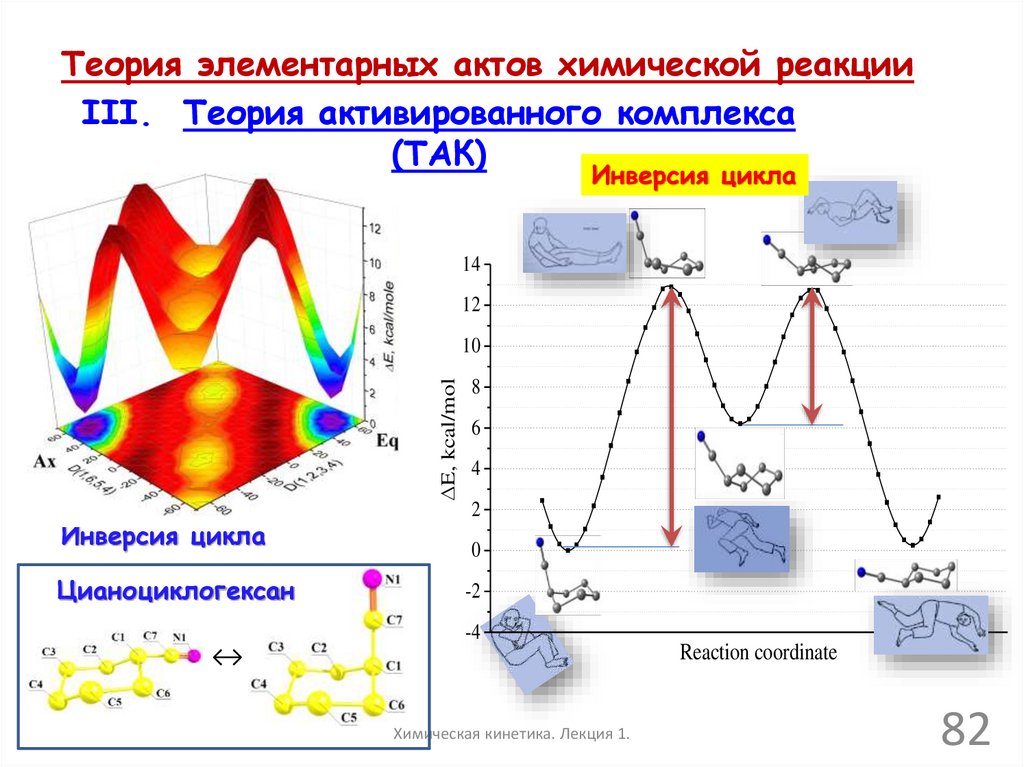
Теория элементарных актов химической реакции
III. Теория активированного комплекса
(ТАК)
Инверсия цикла
14
12
E, kcal/mol
10
Инверсия цикла
Цианоциклогексан
8
6
4
2
0
-2
-4
Reaction coordinate
↔
Химическая кинетика. Лекция 1.
82

83.

Влияние растворителя и катализатора на
скорость химической реакции
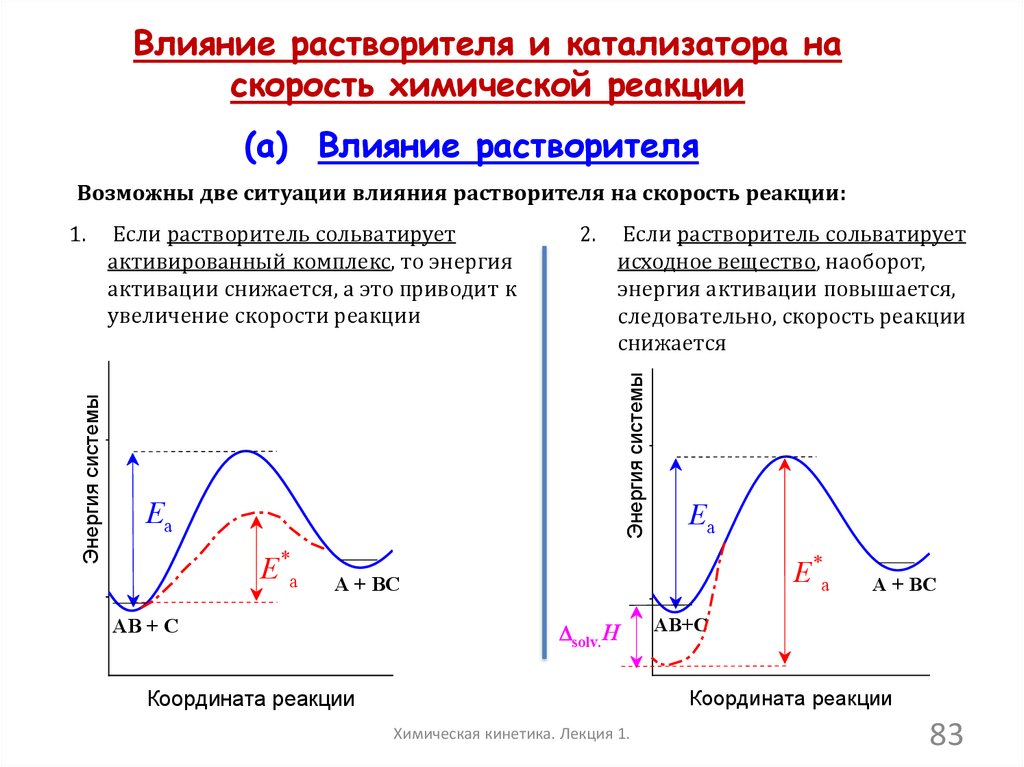
(а) Влияние растворителя
Возможны две ситуации влияния растворителя на скорость реакции:
Если растворитель сольватирует
активированный комплекс, то энергия
активации снижается, а это приводит к
увеличение скорости реакции
2.
Если растворитель сольватирует
исходное вещество, наоборот,
энергия активации повышается,
следовательно, скорость реакции
снижается
Энергия системы
Энергия системы
1.
Ea
E *a
Ea
E*a
A + BC
AB + C
solv.H
A + BC
AB+C
Координата реакции
Координата реакции
Химическая кинетика. Лекция 1.
83

84.

Влияние растворителя и катализатора на скорость химической реакции
(б) Влияние катализатора
Термин «катализ» был предложен в 1834 г. Й. Берцелиусом. В дословном
переводе с греческого catalysis означает прекращение, разрушение, что не
соответствует тому смыслу, который сейчас вкладывается в это понятие.
Существуют различные определения катализа, отражающие различные
стороны каталитического процесса.
В соответствии с современным определением явление катализа состоит в
селективном (избирательном) ускорении химической реакции веществом
(катализатором), которое многократно вступает в промежуточные
взаимодействия с исходными реагентами, но регенерируется к моменту
образования продуктов.
Катализ – явление изменения скорости реакции в присутствии веществ,
состояние и количество которых после реакции остаются неизменными.
Такие вещества называются катализаторами.
Химическая кинетика. Лекция 1.
84

85.

Влияние растворителя и катализатора на скорость химической реакции
(б) Влияние катализатора
Катализатор входит в структуру активированного комплекса, но
стехиометрически не является реагентом.
Следует иметь в виду, что:
• Никакой катализатор не способен сделать возможным
самопроизвольное протекание термодинамически невозможного
процесса (т.е. для которого ∆G>0)
• Катализатор не изменяет константу равновесия для обратимой реакции,
а только ускоряет как прямую, так и обратную реакцию, сокращая тем
самым время достижения химического равновесия.
Химическая кинетика. Лекция 1.
85

86.

Влияние растворителя и катализатора на скорость химической реакции
(б) Влияние катализатора
Основные свойства катализаторов:
1. Специфичность – ускоряет только одну или группу реакций, но при этом
не влияет на скорость других реакций. Например, Pt, Cu, Ni, Fe и др.
катализируют процесс гидрирования, а Al2O3 – гидратацию.
2. Селективность – ускоряет только одну из возможных параллельных
реакций.
Так, например, разложение этилового спирта на различных катализаторах
сопровождается образованием разных продуктов:
Смесь ZnO с Cr2O3 (получаются бутадиен (дивинил) и вода) была предложена С.В.
Лебедевым для процесса получения синтетического каучука путем
полимеризации бутадиена
Химическая кинетика. Лекция 1.
86

87.

Влияние растворителя и катализатора на
скорость химической реакции
(б) Влияние катализатора
Вещества, замедляющие химическую реакцию, называются ингибиторы.
Катализаторы биохимических процессов называются ферменты (энзимы).
Механизм катализа
Катализатор изменяет механизм реакции!!!
• Катализатор образует промежуточное вещество (активированный
комплекс)
• Энергия активации этого процесса ниже, чем если бы реакция протекала без
участия катализатора.
• Это понижение энергии активации укоряет протекание реакции.
Химическая кинетика. Лекция 1.
87

88.

Влияние растворителя и катализатора на
скорость химической реакции
(б) Влияние катализатора
Энергия системы
[A...B]
Ea
[A...B...Кат.]
Eа, Кат.
AB + Кат.
A + B + Кат.
Энергия системы
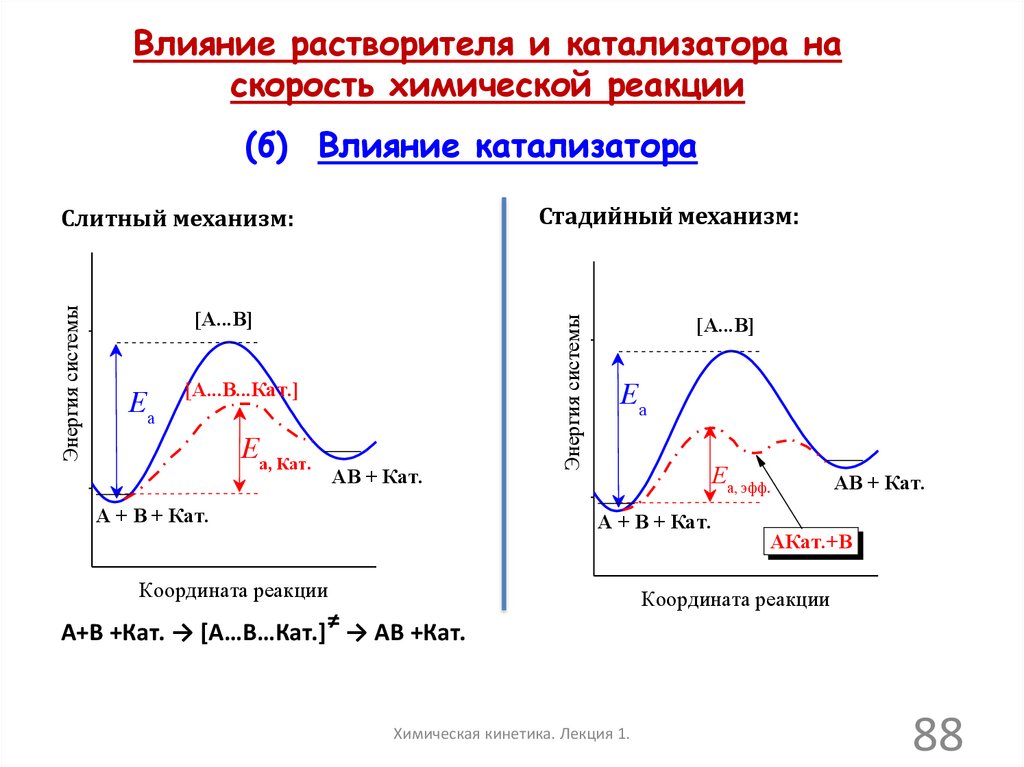
Стадийный механизм:
Слитный механизм:
[A...B]
Ea
Еа, эфф.
A + B + Кат.
Координата реакции
А+В +Кат. → [A…B…Кат.]≠ → АВ +Кат.
Химическая кинетика. Лекция 1.
AB + Кат.
AКат.+B
Координата реакции
88

89.

Влияние растворителя и катализатора на
скорость химической реакции
(б) Влияние катализатора
Уравнение Михаэлиса-Ментен
Рассмотрим простейшую мономолекулярную реакцию:
S→P
в присутствии катализатора Е:
Здесь общая концентрация катализатора равна сумме концентраций
свободной и связанной формы: С = С + С
E0
E
SE
ив метод квазистационарных концентраций:
Получим:
Уравнение Михаэлиса-Ментен
Химическая кинетика. Лекция 1.
89

90.

Влияние растворителя и катализатора на
скорость химической реакции
(б) Влияние катализатора
Ферменты
Ферменты являются гомогенными биологическими катализаторами. Эти
вездесущие соединения представляют собой особые белки или нуклеиновые
кислоты, которые содержат активный центр, ответственный за связывание
субстратов, реагентов, и переработку их в продукты.
Как и в случае с любым катализатором, активный центр возвращается в
исходное состояние после высвобождения продуктов.
Многие ферменты состоят в основном из белков, некоторые из которых
содержат органические или неорганические кофакторы в своих активных
центрах. Однако некоторые молекулы РНК также могут быть биологическими
катализаторами, образующими рибозимы. Очень важным примером рибозима
является рибосома, большое собрание белков и каталитически активных
молекул РНК, ответственных за синтез белков в клетке.
Химическая кинетика. Лекция 1.
90

91.

Влияние растворителя и катализатора на скорость химической реакции
(б) Влияние катализатора
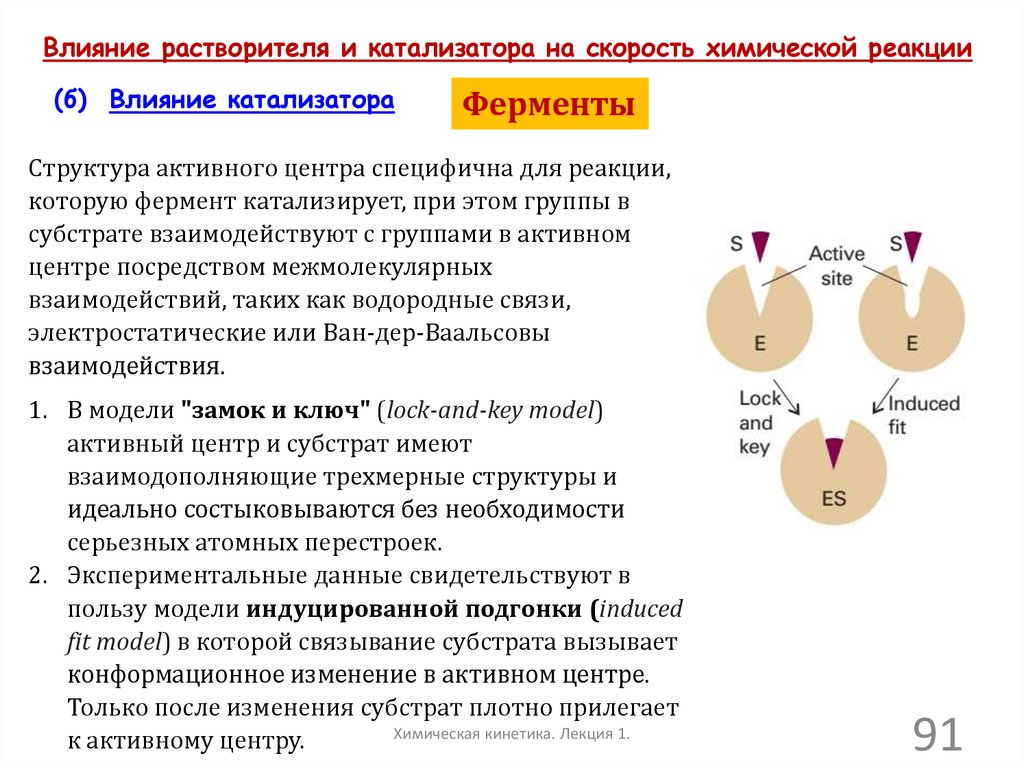
Ферменты
Структура активного центра специфична для реакции,
которую фермент катализирует, при этом группы в
субстрате взаимодействуют с группами в активном
центре посредством межмолекулярных
взаимодействий, таких как водородные связи,
электростатические или Ван-дер-Ваальсовы
взаимодействия.
1. В модели "замок и ключ" (lock-and-key model)
активный центр и субстрат имеют
взаимодополняющие трехмерные структуры и
идеально состыковываются без необходимости
серьезных атомных перестроек.
2. Экспериментальные данные свидетельствуют в
пользу модели индуцированной подгонки (induced
fit model) в которой связывание субстрата вызывает
конформационное изменение в активном центре.
Только после изменения субстрат плотно прилегает
Химическая кинетика. Лекция 1.
к активному центру.
91

92.

Влияние растворителя и катализатора на скорость химической реакции
(б) Влияние катализатора
Ферменты
Реакции, катализируемые ферментами, склонны к ингибированию
молекулами, которые препятствуют образованию продукта.
Многие лекарственные средства для лечения заболеваний
действуют путем ингибирования ферментов.
Например, важная стратегия лечения синдрома приобретенного
иммунодефицита (СПИД) включает постоянное введение
специально разработанного ингибитора протеазы.
Препарат ингибирует фермент, который является ключевым для
формирования белковой оболочки, окружающей генетический
материал вируса иммунодефицита человека (ВИЧ).
Без правильно сформированной оболочки ВИЧ не может
реплицироваться в организме «хозяина».
Химическая кинетика. Лекция 1.
92

93.

Кинетика ионных реакций в растворах
Предположим, что в водном растворе протекает химическая реакция c
участием ионов вида:
где zA, zB, zD, zE – заряды частиц.
В соответствии с выражением для константы скорости в теории
активированного комплекса (ТАК), см. слайд № 80:
(1)
Согласно термодинамике неидеальных систем константа
равновесия для реакций с участием ионов должна
выражаться не через концентрации, а через активности:
(2)
Химическая кинетика. Лекция 1.
93

94.

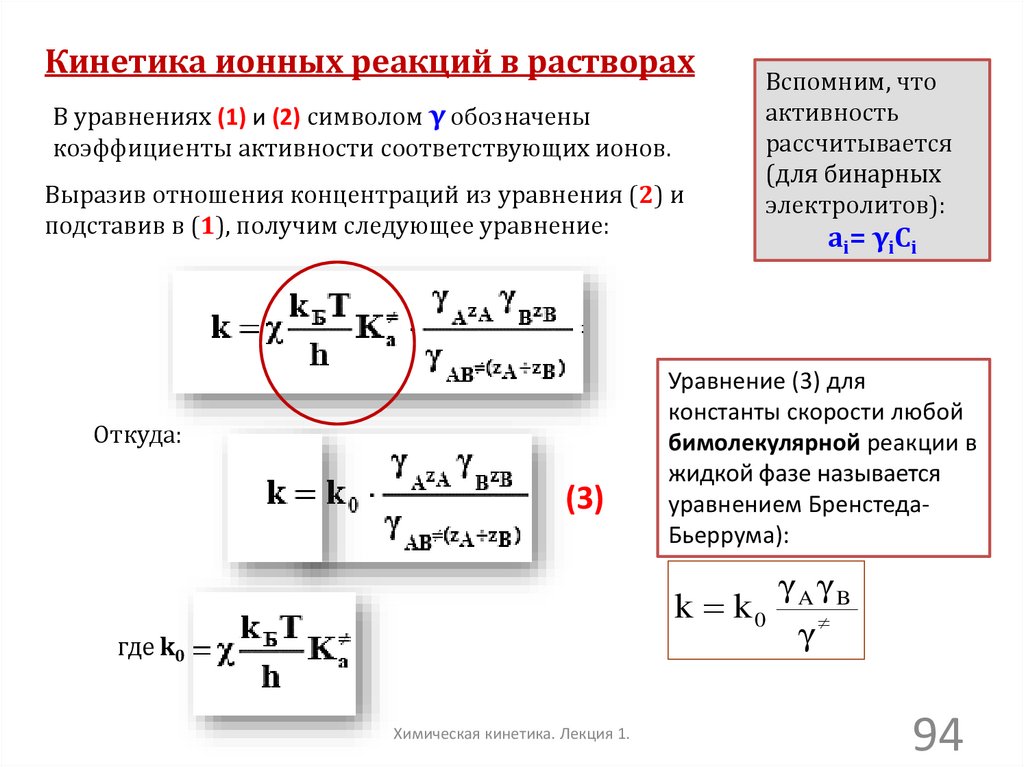
Кинетика ионных реакций в растворах
В уравнениях (1) и (2) символом γ обозначены
коэффициенты активности соответствующих ионов.
Выразив отношения концентраций из уравнения (2) и
подставив в (1), получим следующее уравнение:
Откуда:
(3)
Вспомним, что
активность
рассчитывается
(для бинарных
электролитов):
ai= γiCi
Уравнение (3) для
константы скорости любой
бимолекулярной реакции в
жидкой фазе называется
уравнением БренстедаБьеррума):
γAγB
k k0
γ
где k0
Химическая кинетика. Лекция 1.
94

95.

Кинетика ионных реакций в растворах
(3)
Согласно теории сильных электролитов Дебая и Хюккеля, коэффициент
активности иона в водном растворе приближенно может быть выражен
следующим образом:
(4)
где z – заряд иона, I – ионная сила раствора: I
1
Σ(m i Zi2 )
2
Логарифмируя уравнение (3) и подставляя выражения для
коэффициентов активности ионов в соответствии с уравнением (4) ,
получаем следующее уравнение:
Откуда:
(5)
Химическая кинетика. Лекция 1.
95

96.

Кинетика ионных реакций в растворах
(5)
Таким образом, для реакции между ионами:
логарифм константы скорости оказывается линейной функцией
квадратного корня из ионной силы.
На рисунке приведены зависимости для различных значений произведений
зарядов реагирующих ионов:
k
lg
k0
ZA·ZB >0
ZA·ZB =0
I
ZA·ZB <0
Химическая кинетика. Лекция 1.
96

97.

Кинетика ионных реакций в растворах
k
lg
1,02 Z A Z B I
k0
(5)
В соответствии с теорией для ионов, обладающих одинаковым по
знаку зарядом (неважно, «+» или « » ), логарифм константы
скорости растет с ростом I, причем тем сильнее, чем больше по
абсолютной величине произведение зарядов.
Если взаимодействующие ионы имеют противоположные заряды, то
наблюдается уменьшение логарифма константы скорости с
увеличением I.
При взаимодействии иона с незаряженной частицей логарифм
константы скорости не зависит от ионной силы раствора.
Химическая кинетика. Лекция 1.
97

98.

Кинетика ионных реакций в растворах
Необходимо отметить, что указанные зависимости хорошо
соблюдаются на практике, что является подтверждением теории
активированного комплекса.
Ионная сила раствора зависит от концентрации всех присутствующих
в растворе ионов, а не только от участников реакции. Поэтому
скорость реакции может изменяться при добавлении в раствор
посторонних электролитов.
Влияние добавки постороннего вещества на скорость реакции в
растворе посредством изменения его ионной силы называется
первичным солевым эффектом.
Возможен вторичный солевой эффект, заключающийся в воздействии
добавляемого электролита на концентрацию одного из реагентов, что
приводит к изменению скорости реакции.
Химическая кинетика. Лекция 1.
98

99.

Кинетика ионных реакций в растворах
В 1966 г. Брауну и Дейтону удалось использовать уравнение
(5) для доказательства существования в водном растворе
сольватированного электрона (есольв). В опытах он был получен
воздействием на водный раствор γ-облучения.
Было обнаружено, что:
при взаимодействии есольв с Ag+ или СН3О+ константа
скорости линейно понижается,
при взаимодействии с одноименно заряженной частицей,
например, с NO2– возрастает
Всё это могло быть истолковано только как результат
взаимодействия ионов с реально существующей частицей
Химическая кинетика. Лекция 1.
99

100.

Кинетика ионных реакций в растворах
При электростатистическом взаимодействии заряженных частиц
(диполей или ионов) с полярными молекулами растворителя вокруг
частиц возникают сольватные оболочки.
Кирквудом было выведено уравнение, определяющее величину
работы, затраченной на создание сольватной оболочки:
(6)
где μ– дипольный момент; r – радиус полярной молекулы;
ε – диэлектрическая проницаемость среды.
Подстановка выражения (6) в уравнение Бренстеда-Бьеррума дает
известную формулу Кирквуда для константы скорости реакции
взаимодействия двух полярных молекул с дипольными моментами μА
и μА , образующих промежуточный продукт (активированный комплекс)
с дипольным моментом μ≠:
(7)
Химическая кинетика. Лекция 1.
100

101.

Кинетика ионных реакций в растворах
(7)
Графики зависимости lnk
от параметра уравнения
Кирквуда
Если μ2≠ > μА2 + μB2 , , то соблюдается
линейная зависимость с
положительным угловым
коэффициентом (прямая 2 на рисунке)
Если μ2≠ < μА2 + μB2 , то угловой
коэффициент отрицателен (прямая 1)
Химическая кинетика. Лекция 1.
101