Похожие презентации:
Неопределенный интеграл. Определения и теоремы
1. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
1.Определение и свойстванеопределенного интеграла
2. Определения и теоремы:
Определение. Первообразной функцией дляданной функции f(x) на данном промежутке
называется, такая функция F(x),
производная которой равна f(x) или
дифференциал которой равен f(x)dx на
рассматриваемом промежутке.
3.
Теорема. Две различные первообразныеодной и той же функции, определенной в
некотором промежутке, отличаются друг от
друга на этом промежутке на const.
4.
Определение. Общее выражение для всехпервообразных данной непрерывной
функции f(x) называется неопределенным
интегралом от функции f(x) или от
дифференциального выражения f(x)dx и
обозначается символам f (x)dx .
f (x)dx F (x) C
5. Свойства неопределенного интеграла
1.Если непрерывно дифференцируемаяфункция, то
d
(
x
)
(
x
)
C
2.
d f x dx f x dx
f x dx ' f x
Af
(
x
)
dx
A
f
(
x
)
dx
6.
3. Неопределенный интеграл оталгебраической суммы конечного числа
непрерывных функций равен
алгебраической сумме неопределенных
интегралов от этих функций.
7. 2.Таблица простейших неопределенных интегралов
Таблица интегралов8.
1.m
1
u
m
u du m 1 C,m 1
2.
du lnu C
u
9.
3.4.
5.
u
u
e
du
e
C
u
a
u
a du lna C
cos udu sin u C
10.
6.7.
8.
sin
udu
cos
u
C
du tgu C
cos 2u
du ctgu C
sin 2u
11.
9.du arcsinu C arccosu C
1 u2
10.
du arctgu C arcctgu C
1 u 2
12. Дополнительные формулы:
1.du 1 ln a u Ca
a2 u2 2a a u
2.
du 1 ln a u C
u2 a2 2a a u
13.
3.du lnu u2 a C
u2 a
du
u
arcsin
C
4.
a
2
2
\ / a u
du 1 arctg u C
5. a2 u2 a
a
14. 3.Основные методы интегрирования :
1.Метод разложения.Пусть
f x f x f x
1 2
, тогда
f x dx f1 x dx f 2 x dx
15.
2.Метод подстановки (метод введенияновой переменной)
t dt
f
x
dx
f
t
'
16.
3.Метод интегрирования по частям.udv
uv
vdu
17. Неберущиеся интегралы
Sinx ln xdx e dxCosx ln xdx e dx
dx
Cosx
ln x
dx
x
x2
x
2
18. Теорема Коши
• Теорема: Всякая непрерывная функцияимеет первообразную (от всякой
непрерывной функции существует
неопределенный интеграл).







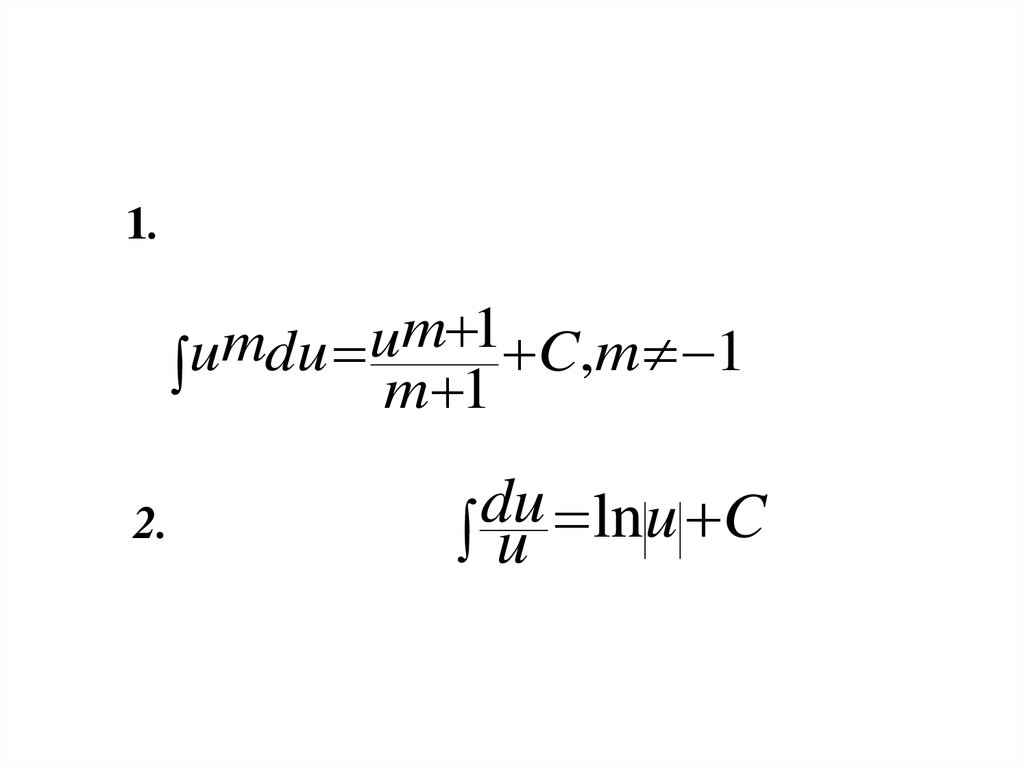

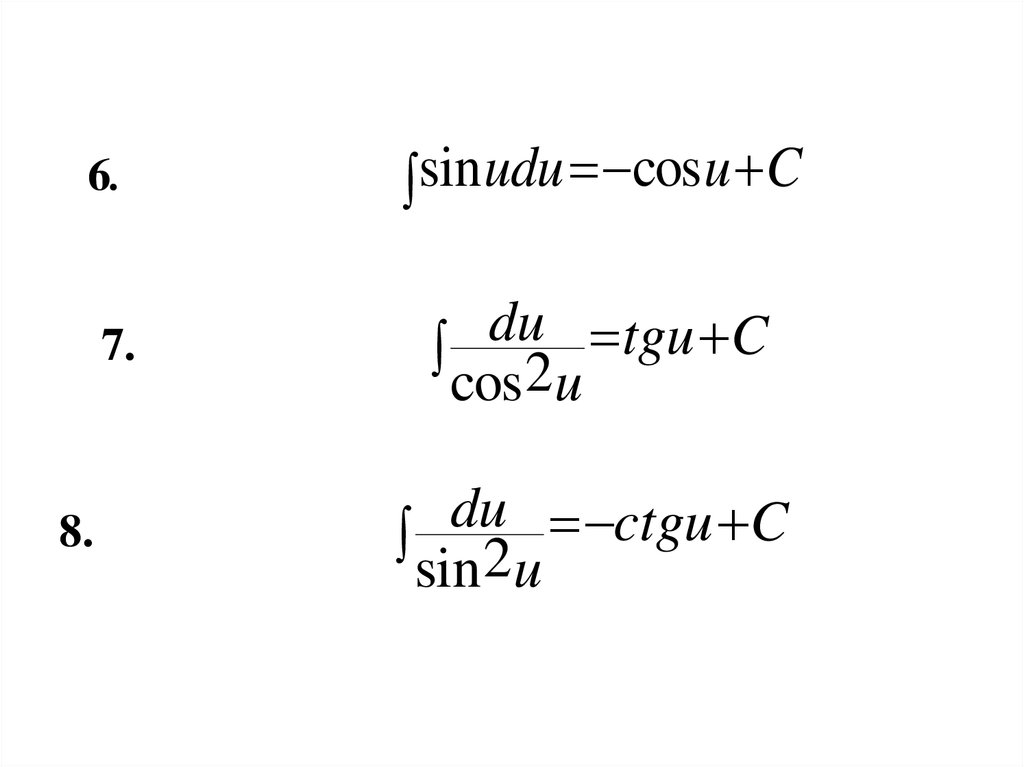


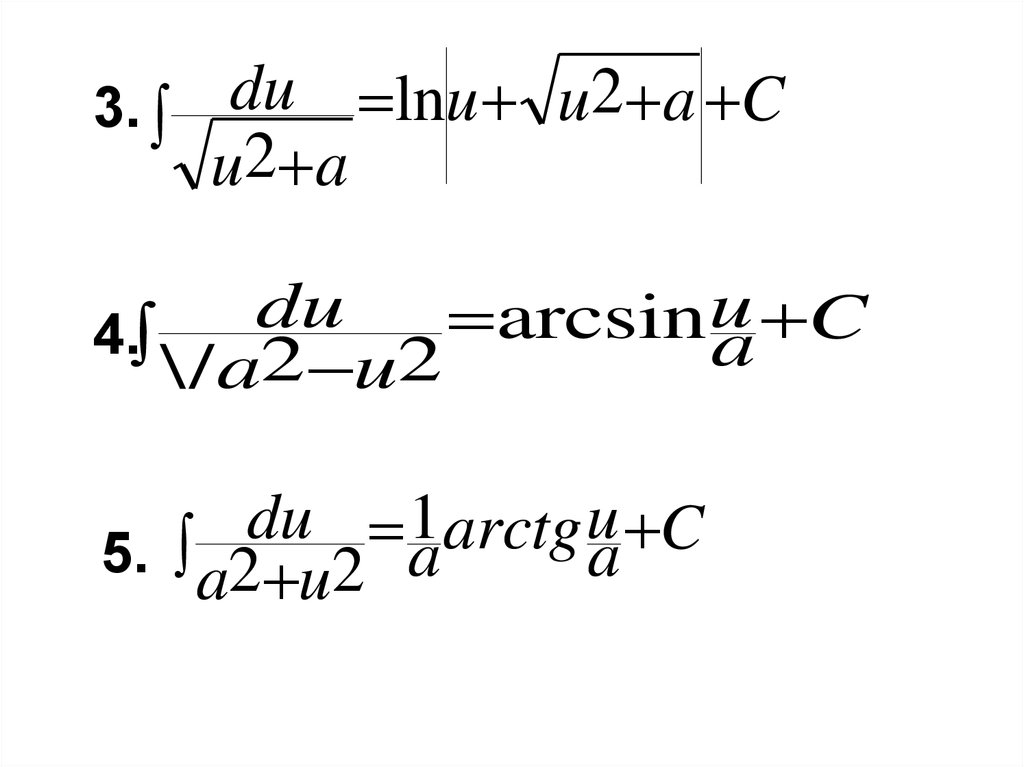


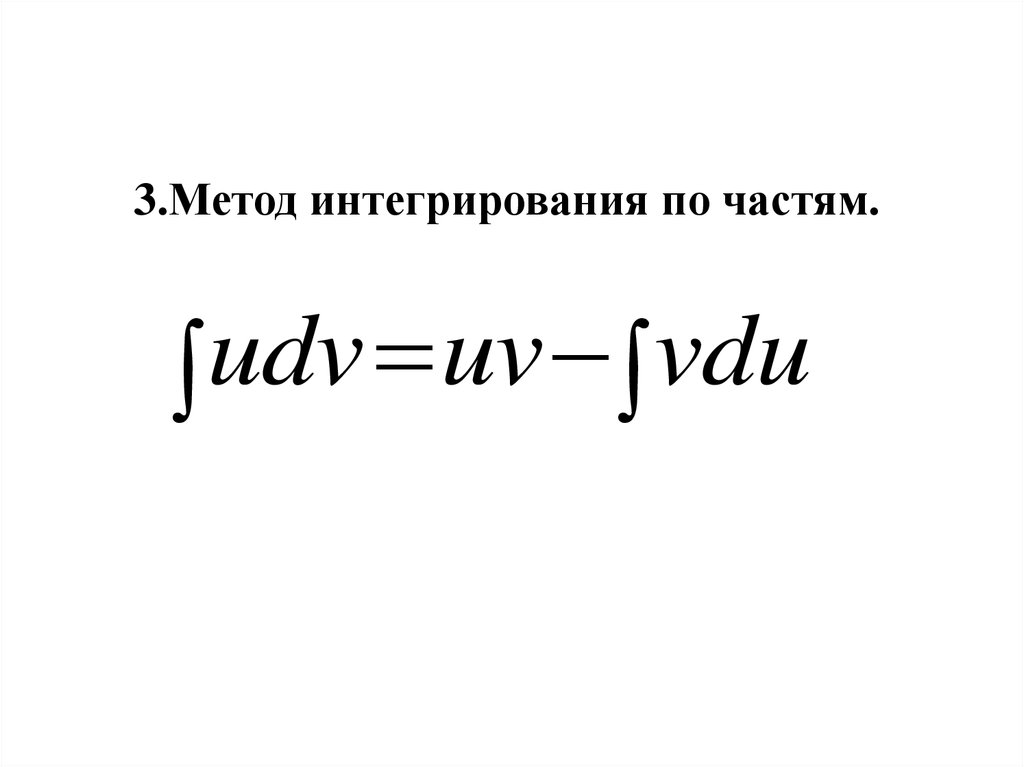


 Математика
Математика








