Похожие презентации:
Решение иррациональных уравнений с параметром
1. Решение иррациональных уравнений с параметром.
2.
3.
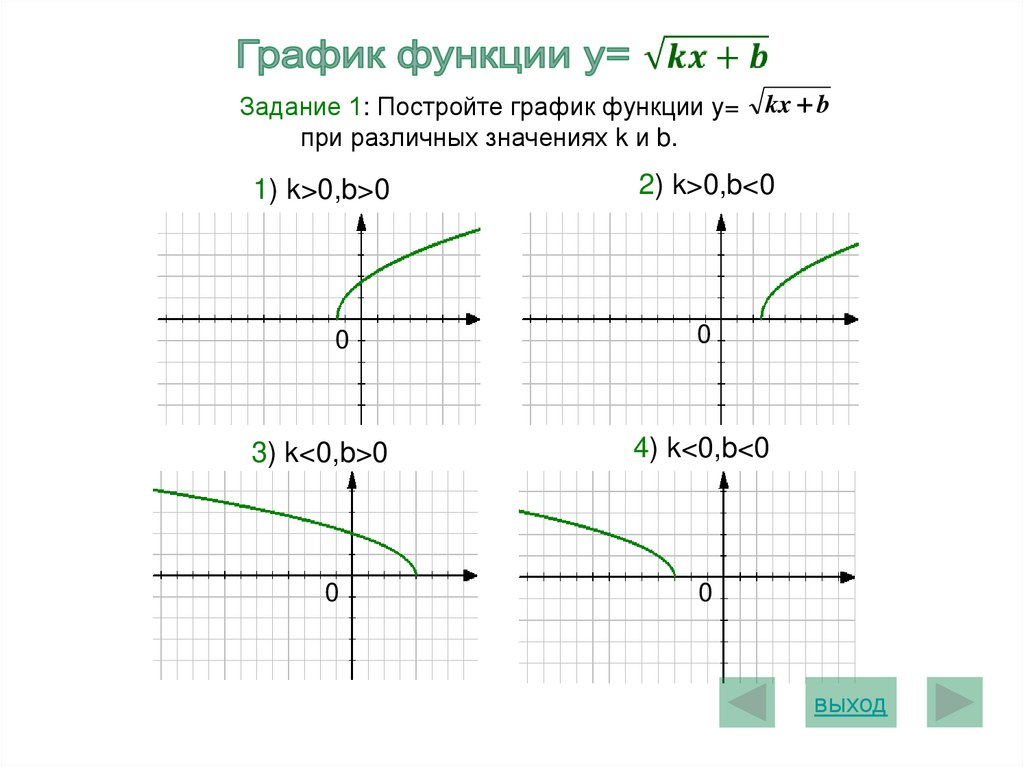
Задание 1: Постройте график функции y=при различных значениях k и b.
1) k>0,b>0
0
kx b
2) k>0,b<0
0
3) k<0,b>0
4) k<0,b<0
0
0
выход
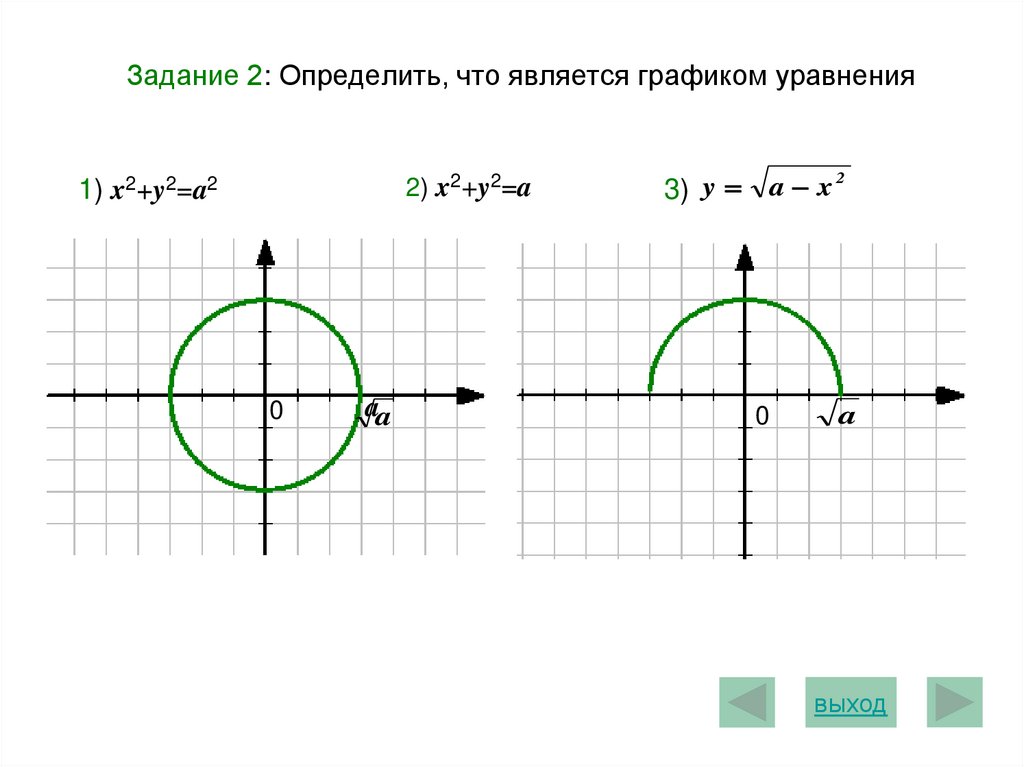
4. Задание 2: Определить, что является графиком уравнения
2) x2+y2=a1) x2+y2=a2
0
aa
2
3) y a x
0
a
выход
5.
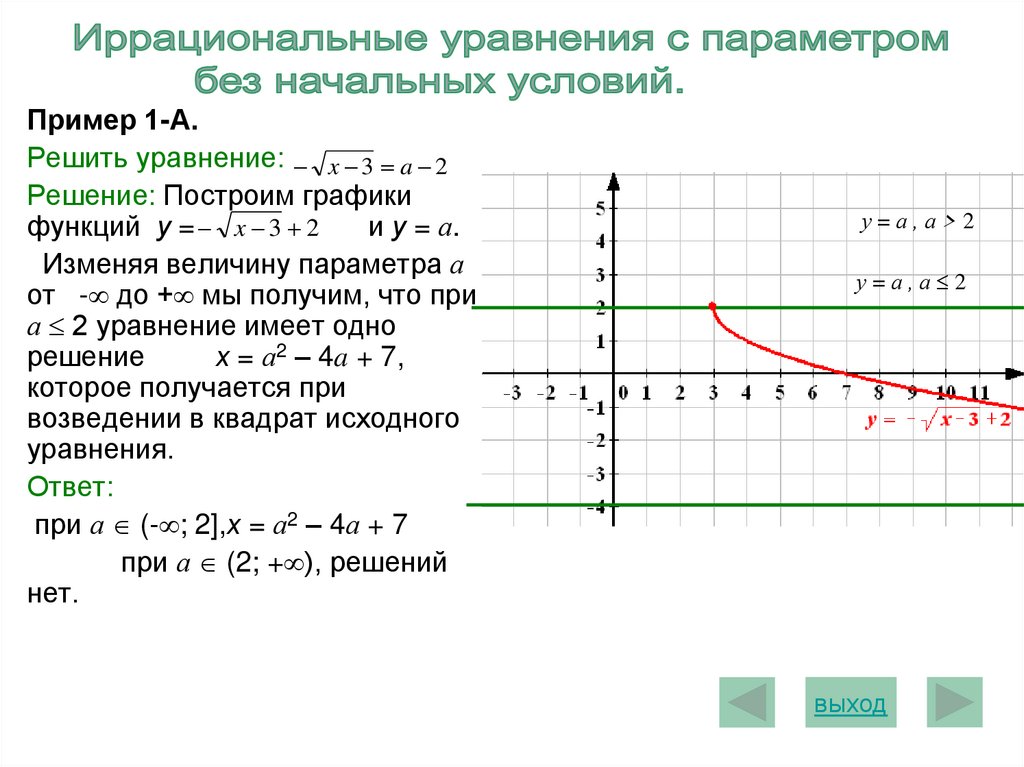
Пример 1-А.Решить уравнение: x 3 a 2
Решение: Построим графики
функций у = x 3 2
и у = а.
Изменяя величину параметра а
от - до + мы получим, что при
а 2 уравнение имеет одно
решение
х = а2 – 4a + 7,
которое получается при
возведении в квадрат исходного
уравнения.
Ответ:
при а (- ; 2],х = а2 – 4а + 7
при а (2; + ), решений
нет.
у=а,а>2
у=а,а 2
выход
6.
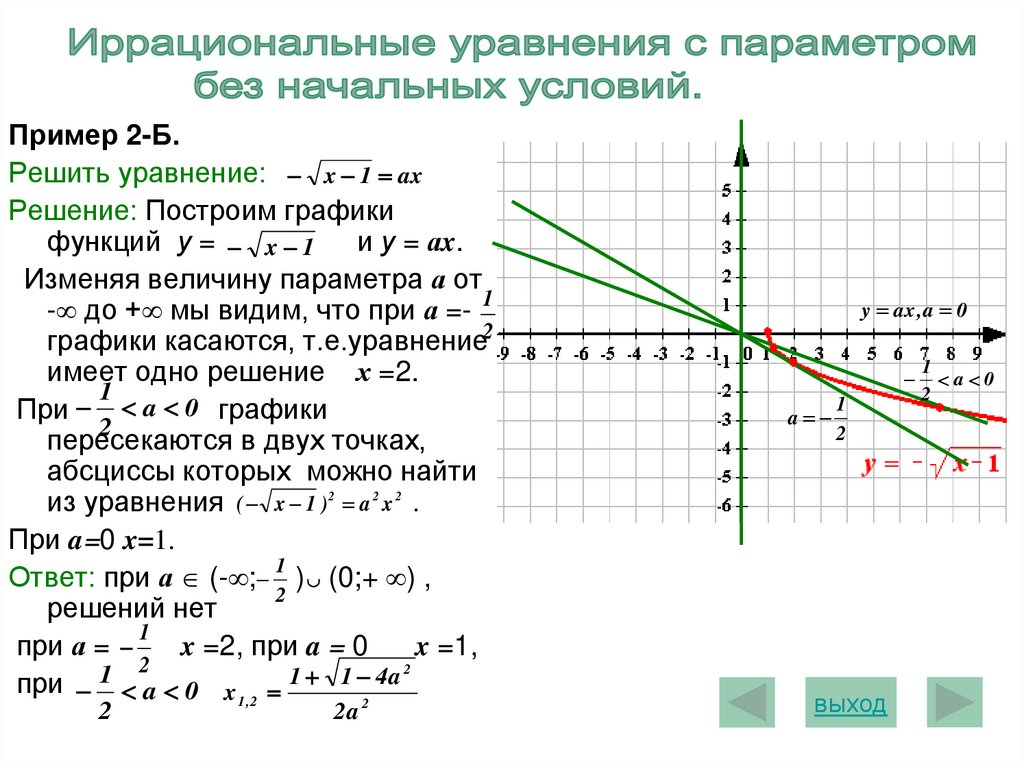
Пример 2-Б.Решить уравнение: x 1 ax
Решение: Построим графики
функций у = x 1 и у = аx.
Изменяя величину параметра а от
- до + мы видим, что при а =- 1
графики касаются, т.е.уравнение2
имеет одно решение х =2.
1
При a 0 графики
2
пересекаются в двух точках,
абсциссы которых можно найти
из уравнения ( x 1 )2 a 2 x 2 .
При a=0 x=1.
1
Ответ: при а (- ; ) (0;+ ) ,
2
решений нет
1
при а =
x =2, при a = 0
x =1,
2
2
при 1 a 0 x 1 ,2 1 1 4 a
2
2a 2
y ax , a 0
a
1
2
выход
1
a 0
2
7.
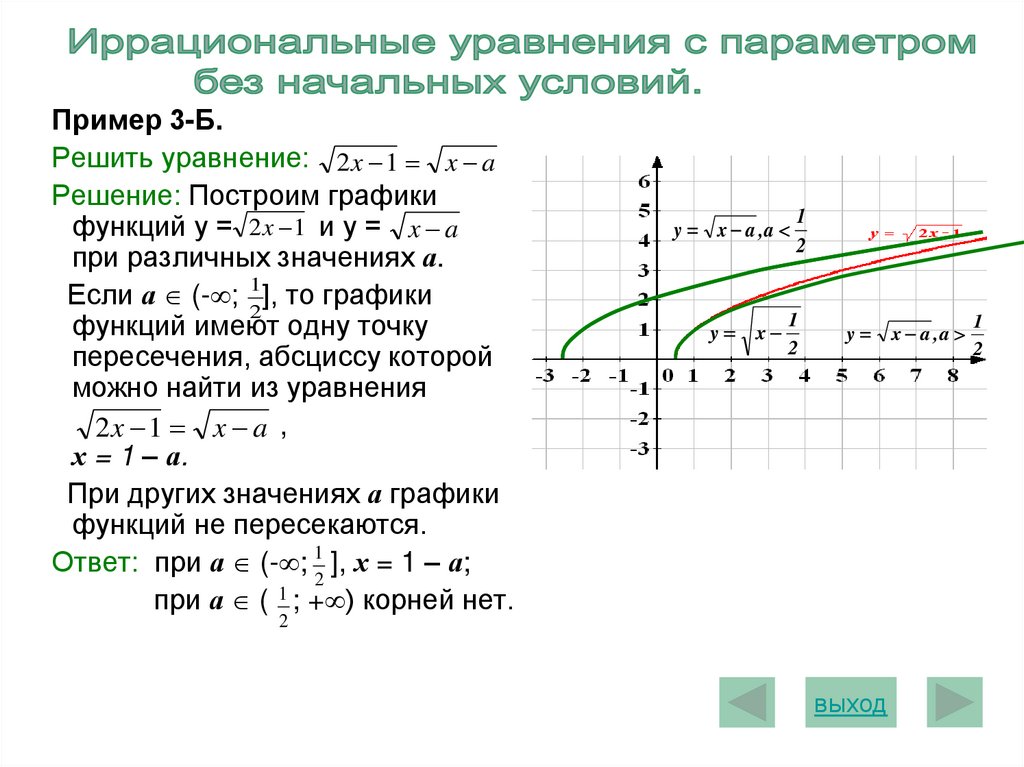
Пример 3-Б.Решить уравнение: 2 x 1 x a
Решение: Построим графики
функций у = 2 x 1 и у = x a
при различных значениях а.
Если а (- ; 12], то графики
функций имеют одну точку
пересечения, абсциссу которой
можно найти из уравнения
2 x 1 x a ,
х = 1 – а.
При других значениях а графики
функций не пересекаются.
Ответ: при а (- ; 12 ], х = 1 – а;
при а ( 1 ; + ) корней нет.
y x a ,a
y
x
1
2
1
2
y
2
выход
x a ,a
1
2
8.
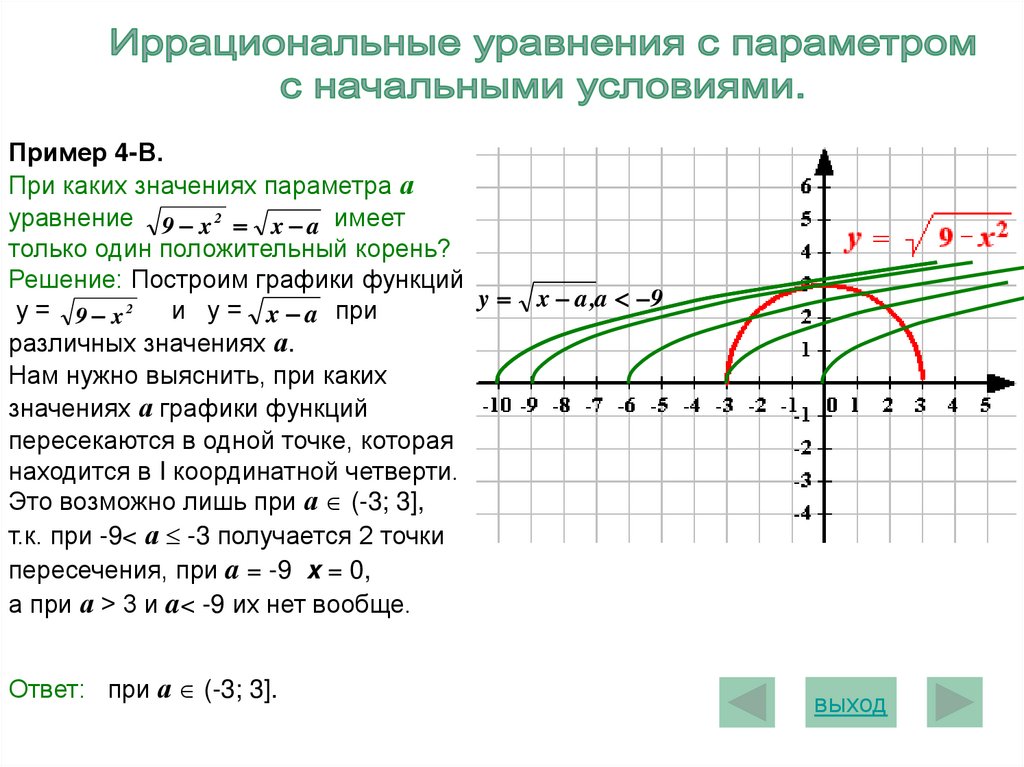
Пример 4-В.При каких значениях параметра а
уравнение 9 x 2 x a имеет
только один положительный корень?
Решение: Построим графики функций
y
у = 9 x2
и у = x a при
различных значениях а.
Нам нужно выяснить, при каких
значениях а графики функций
пересекаются в одной точке, которая
находится в I координатной четверти.
Это возможно лишь при а (-3; 3],
т.к. при -9< а -3 получается 2 точки
пересечения, при a = -9 x = 0,
а при а > 3 и a< -9 их нет вообще.
Ответ: при а (-3; 3].
x a ,a 9
выход
9.
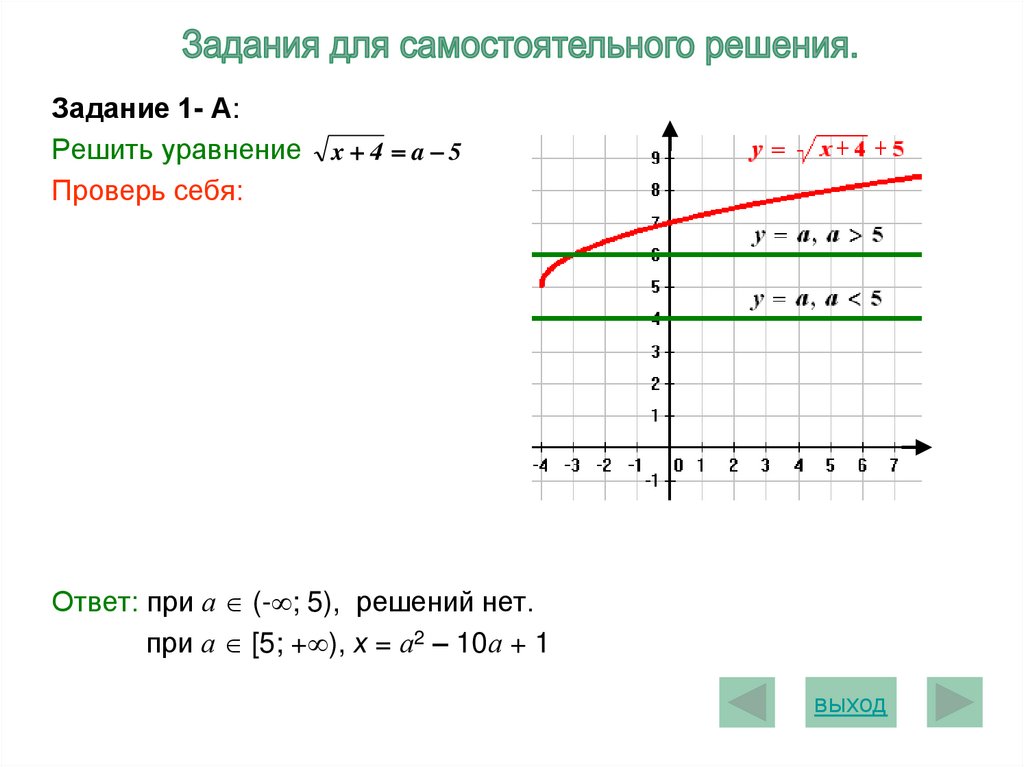
Задание 1- А:Решить уравнение
Проверь себя:
x 4 a 5
Ответ: при а (- ; 5), решений нет.
при а [5; + ), х = а2 – 10а + 1
выход
10.
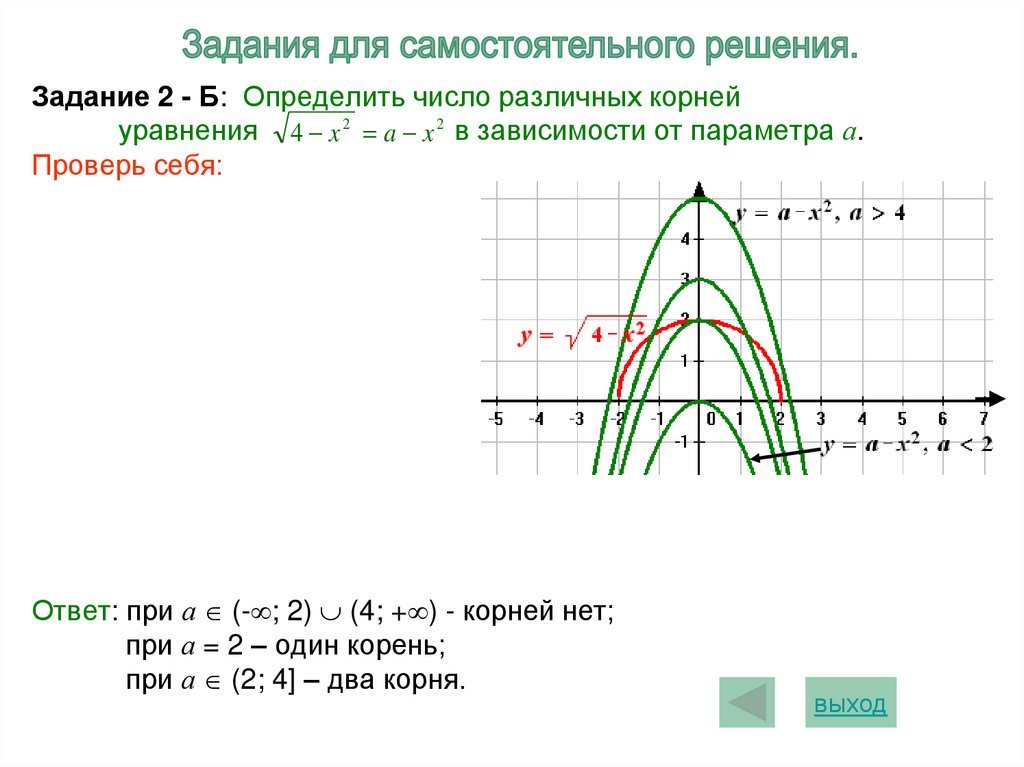
Задание 2 - Б: Определить число различных корнейуравнения 4 x 2 a x 2 в зависимости от параметра а.
Проверь себя:
Ответ: при а (- ; 2) (4; + ) - корней нет;
при а = 2 – один корень;
при а (2; 4] – два корня.
выход


 Математика
Математика








