Линейное программирование. (Лекция 1)

1.

Лекция 1
1.Общая задача линейного программирования
2. Система m линейных уравнений с n переменными,
основные (базисные) и неосновные (свободные) переменные.
Базисные решения.
3.Геометрический смысл решений линейных неравенств и их
систем.

2.

1.Общая задача линейного программирования
Дана система m линейных уравнений и неравенств с n
переменными
a11 x1 a12 x2 ...
a21 x1 a22 x2 ...
a1n xn b1
a2 n xn b2
…………………………………………..
ak1 x1 ak 2 x2 ...
akn xn bk
a k 1,1 x1 a k 1, 2 x 2 ... a k 1,n x n bk 1
…………………………………………..
am1 x1 am 2 x2 ... amn xn bm
и
линейная функция
F c1 x1 c2 x2 ... cn xn

3.

Необходимо найти такое решение системы
x j 0, j 1,2,..., l ; l n
X x1 , x2 ,..., xn
при котором линейная функция принимает оптимальное (т.е.
максимальное или минимальное) значение .
Оптимальное решение иногда называют оптимальным планом
(экономическая интерпретация).
Рассматривают различные формы задач линейного
программирования.
Если все переменные неотрицательны и система ограничений
состоит лишь из одних неравенств, то задача называется стандартной.
Если система ограничений состоит из одних уравнений, то задача
называется канонической.
Любая задача линейного программирования может быть сведена к
канонической, стандартной или общей задаче.

4.

2. Система m линейных уравнений с n переменными,
основные (базисные) и неосновные (свободные) переменные). Базисные
решения.
Рассмотрим систему
a11 x1 a12 x2 ... a1n xn b1
a21 x1 a22 x2 ... a2 n xn b2
………..……………………………………………
(1.1)
am1 x1 am 2 x2 ... amn xn bm
Будем считать, что в системе (1.1) все m уравнений линейно
независимы, т.е. r = m (r - ранг системы) и m < n .
Определение. Любые m переменных системы (1.1) называются
основными (или базисными), если определитель матрицы
коэффициентов при них отличен от нуля. Тогда остальные n - m
переменных называются неосновными (или свободными).
Замечание. Максимально возможное число групп основных переменных
не превосходит числа всех сочетаний из n по m
n!
C
m! n m !
m
n

5.

Теорема. Если для системы m линейных уравнений с n переменными
(1.1 ) существует хотя бы одна группа базисных переменных, то эта
система является неопределенной, причем каждому произвольному
набору значений cвободных переменных соответствует одно
решение системы.
Д. Пусть x1,x2,…,xm - базисные переменные. Запишем систему уравнений в
виде
a11 x1 a12 x 2 ... a1m x m b1 a1,m 1 x m 1 ... a1n x n
a 21 x1 a 22 x 2 ... a 2 m x m b2 a 2,m 1 x m 1 ... a 2 n x n
………………………………………………………………
a m1 x1 a m 2 x 2 ... a mm x m bm a m,m 1 x m 1 ... a mn x n
При произвольном наборе значений переменных xm+1 ,xm+2,…,xn получаем
систему

6.

a11 x1 a12 x 2 ... a1m x m b1'
a 21 x1 a 22 x 2 ... a 2 m x m b2'
…………………………………….
a m1 x1 a m 2 x 2 ... a mm x m bm'
Определитель этой системы
a11
a12
...
a1m
a 21
a 22
... a 2 m
...
...
...
a m1
am2
...
... a mm
0
по теореме Крамера система имеет
единственное решение. В силу произвольного
выбора свободных переменных получаем
бесконечное множество решений.

7.

Решение системы (1.1) называется допустимым, если оно
содержит только неотрицательные компоненты.
Базисным решением системы m уравнений с n переменными
называется решение, в котором все n - m свободных переменных
равны нулю.
Базисное решение, в котором хотя бы одна из основных
переменных равна нулю, называется вырожденным.
Пример. Найти все базисные решения системы уравнений
4!
C42
6 максимальное число пар
x1 2 x2 3x3 x4 0,
2! 2!
базисных переменных
x1 2 x2 x3 3x4 2.
1) x1,x2 -,базисные переменные; x3, x4 – свободные переменные
x1 2 x2 0,
x1 2 x2 2.
1 2
1 2
1 2 1 2 0
x1, x2 не могут быть базисными
переменными
2) x1,x3 - базисные переменные; x2, x4 – свободные переменные
x1 3x3 0,
x1 x3 2.
1
3
x3 , x1
2
2
3 1
X 1 ,0, ,0
2 2
базисное допустимое
решение

8.

x1 2 x2 3x3 x4 0,
x1 2 x2 x3 3x4 2.
3) x1,x4 - базисные переменные; x2, x3 – свободные переменные
x1 x4 0,
x1 3x4 2.
1
1
x1 , x4
2
2
1
1
X 2 ,0,0,
2
2
4) x2 ,x3 - базисные переменные; x1, x4 – свободные переменные
2 x2 3x3 0,
2 x2 x3 2.
3
1
x2 , x3
4
2
3 1
X 3 0, , ,0
4 2
5) x2,x4 - базисные переменные; x1, x3 – свободные переменные
2 x2 x4 0,
2 x2 3x4 2.
1
1
x2 , x4
4
2
1
1
X 4 0, ,0,
2
4
6) x3,x4 - базисные переменные; x1, x2 – свободные переменные
3 x3 x4 0,
x3 3 x4 2.
1
3
x3 , x4
4
4
1 3
X 5 0,0, ,
4 4

9.

3. Геометрический смысл решений линейных неравенств и их
систем.
Теорема. Решением линейного неравенства
a x1 b x2 c
является одна из двух полуплоскостей, на которые прямая
a x1 b x2 c
делит всю плоскость, а также и сама прямая. Вторая полуплоскость
вместе с прямой является решением неравенства
a x1 b x2 c

10.

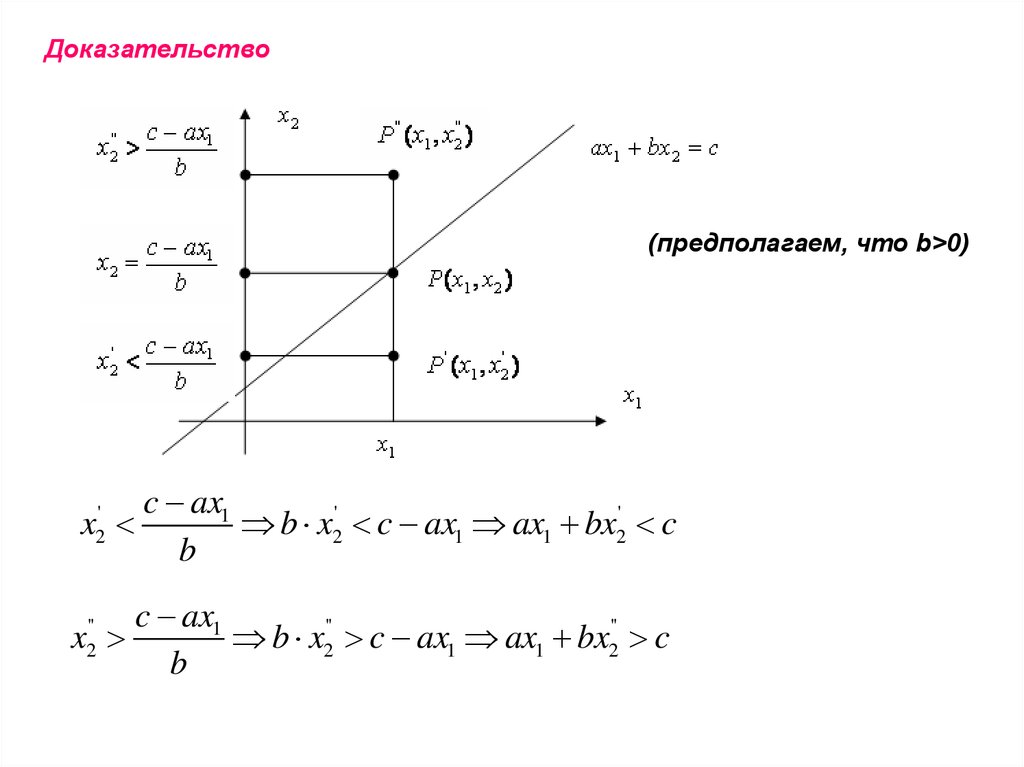
Доказательство
(предполагаем, что b>0)
x2'
c ax1
b x2' c ax1 ax1 bx2' c
b
c ax1
x
b x2'' c ax1 ax1 bx2'' c
b
''
2

11.

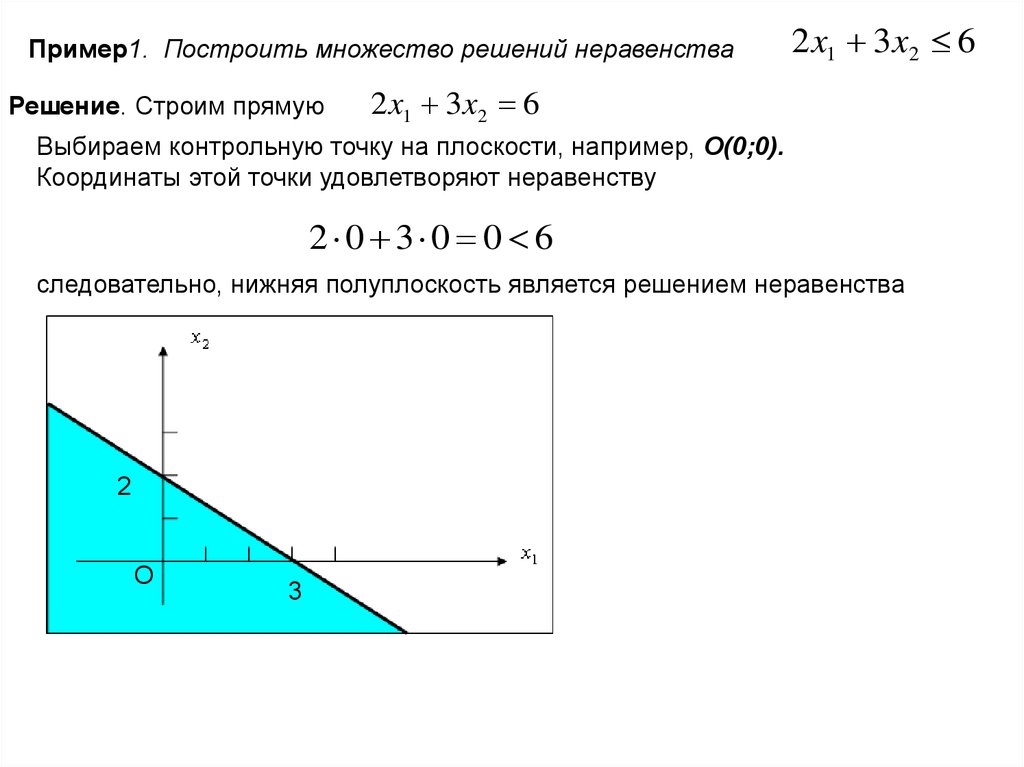
Пример1. Построить множество решений неравенства
Решение. Строим прямую
2 x1 3x2 6
2 x1 3x2 6
Выбираем контрольную точку на плоскости, например, O(0;0).
Координаты этой точки удовлетворяют неравенству
2 0 3 0 0 6
следовательно, нижняя полуплоскость является решением неравенства
2
O
3

12.

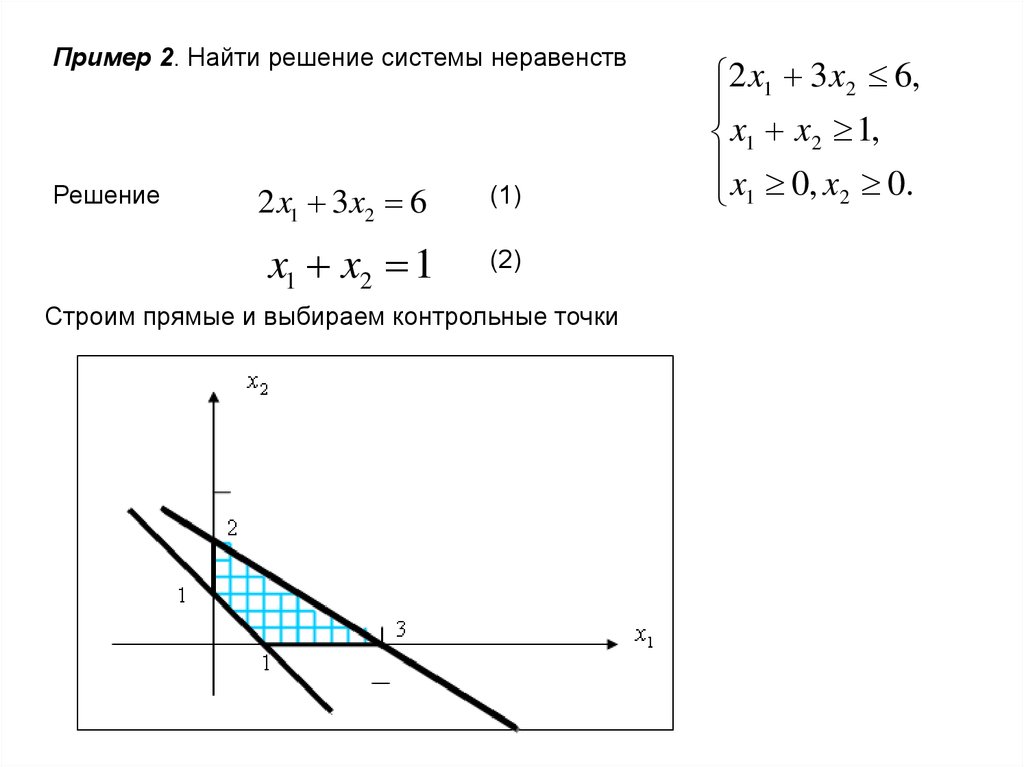
Пример 2. Найти решение системы неравенств
Решение
2 x1 3x2 6
x1 x2 1
(1)
(2)
Строим прямые и выбираем контрольные точки
2 x1 3 x2 6,
x1 x2 1,
x 0, x 0.
2
1

13.

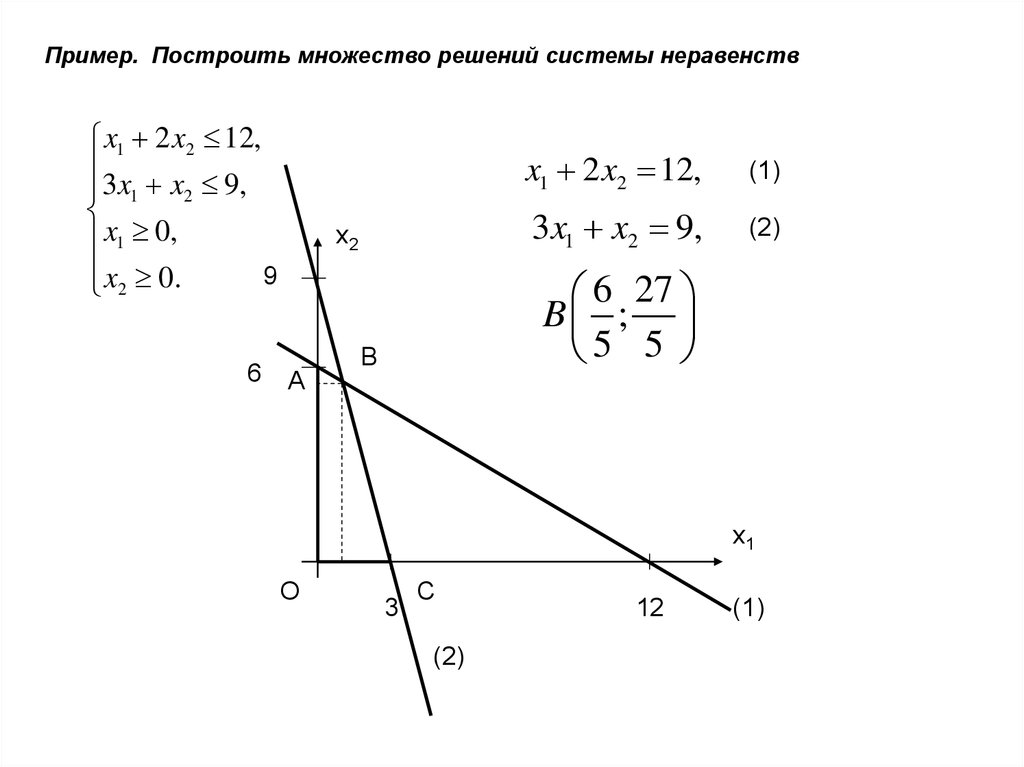
Пример. Построить множество решений системы неравенств
x1 2 x2 12,
3 x x 9,
1 2
x1 0,
x2 0.
9
6
x2
x1 2 x2 12,
(1)
3x1 x2 9,
(2)
6 27
B ;
5 5
B
A
x1
O
3
C
(2)
12
(1)