Кинематика. Основные понятия

1. I. Кинематика. Основные понятия

Кинематика – раздел механики , в котором вводятся методы математического
описания движений, происходит классификация движений,
но не изучаются причины, определяющие вид движения.
Механика – раздел физики, в котором изучаются законы
механического движения и равновесия тел.
Механическое движение – изменение расположения тела
относительно других тел в пространстве
с течением времени.
Телом отсчета называется тело, относительно которого рассматривается
движение других тел. (Одно и то же движение может иметь разный вид
относительно разных тел отсчета, т. е. механическое движение относительно)
Система отсчета — совокупность тела отсчета,
системы координат, связанной с телом отсчета,
Y
S – путь
и часов, неподвижных относительно тела отсчета.
Траектория — линия, по которой движется точка.
Путь — расстояние, пройденное точкой вдоль
траектории.
O
Х
Путь равен длине участка траектории, заключенного между
начальным и конечным положениями точки, если эта точка не
проходит по одному и тому же отрезку
траектории более одного раза.

2.

II. Способы описания положения точки
Для описания положения точки в пространстве существует два основных способа:
1. Координатный способ — положение точки описывается набором чисел,
называемых координатами.
Y
Например, декартовы координаты — набор чисел (x; y; z),
А
или полярные координаты — набор чисел (r; j)
y
А
r
O
Х
x
j
координата точки А по оси ОХ
координата точки А по оси ОY
O
2. Векторный способ — положение точки описывается вектором,
(его называют «радиус-вектор»).
Y
А (x; y)
y
O
rA
x
Радиус-вектор — направленный отрезок,
проведенный из начала координат
в ту точку, положение которой он задает.
Радиус-вектор, задающий положение точки А
Х
Проекции радиус-вектора на координатные оси равны
координатам той точки, положение которой он задает
rx = x ; ry = y ; rz = z

3.

III. Перемещение
Если какая-либо физическая величина изменяется с течением времени, то
Изменением величины называется разность
между ее конечным и начальным значениями.
Изменение величины обозначают символом « D » (дельта):
Da = a2 – a1
Если при движении точки
Da — изменение величины a,
меняется ее координата,
т. е. разность между конечным (a2)
Y
изменение координаты
и начальным (a1) ее значениями
равно Dx = x2 – x1
Радиус-вектор, задающий положение точки,
Dr
r1
тоже меняется, когда эта точка движется.
Перемещением точки называется изменение
ее
r2
радиус-вектора
( Dr )
x
x
(
r
)
т. е. разность между конечным 2 и начальным (r1 )
2
1
O
Х
радиус-векторами:
Dx = x2 – x1
2
1
Dr r r
по правилу вычитания векторов, отложенных из одной точки,
вектор разности проводят
из конца вычитаемого вектора (r1 ) в конец уменьшаемого (r2 )
вектор перемещения проводится
Из рисунка видно, что
из начального положения точки в ее конечное положение
Проекция
вектора перемещения на координатную ось равна
Drx = Dx ; Dry = Dy ; Drz = Dz
изменению координаты точки по этой оси:

4.

IV. Равномерное движение
Равномерным называется движение, при котором точка
за любые равные промежутки времени
S1
проходит одинаковые пути.
S3
S2
То есть, если промежутки времени Dt1=
, Dt2 =
и Dt3 равны друг другу, то пути,
которые точка проходит за эти промежутки времени, S1 ,= S2 и
= S3 тоже равны.
Важно отметить, что промежутки времени Dt1, Dt2 и др. могут быть любыми,
т. е. иметь любую длительность и начинаться с любого момента движения.
Модулем скорости равномерного движения называется отношение
пути, пройденного точкой,
ко времени, за которое пройден этот путь.
путь, пройденный точкой
за время t.
Единица измерения скорости в СИ: 1 м/с
1 м/с — это скорость такого равномерного движения,
При условии, что
при котором точка за каждую секунду
v
=
const
движение равномерно.
проходит путь 1 м.
S
v
t
Если движение равномерно, то с какого бы момента мы ни начали отсчет
промежутка времени t, путь S, пройденный за это время,
будет одним и тем же. Значит, модуль скорости (v = S/t) будет одним и тем же
в любой момент равномерного движения.
Модуль скорости при равномерном движении не изменяется.

5.

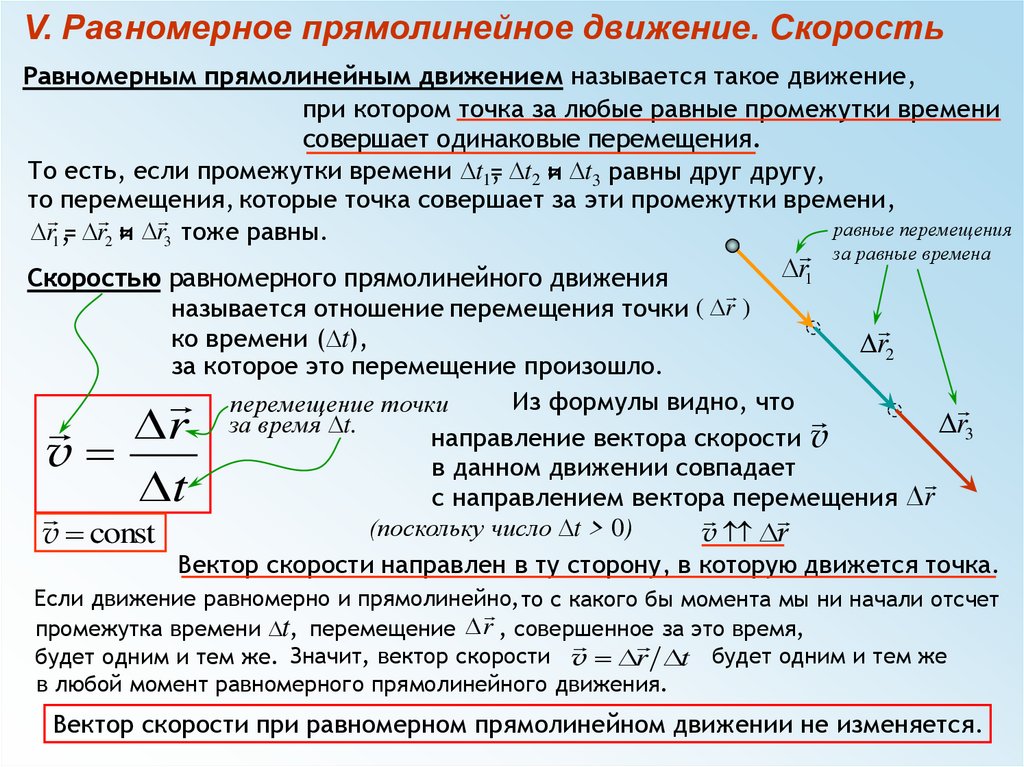
V. Равномерное прямолинейное движение. Скорость
Равномерным прямолинейным движением называется такое движение,
при котором точка за любые равные промежутки времени
совершает одинаковые перемещения.
То есть, если промежутки времени Dt1=
, Dt2 =
и Dt3 равны друг другу,
то перемещения, которые точка совершает за эти промежутки времени,
равные перемещения
Dr1 ,= Dr2 =и Dr3 тоже равны.
Dr1
за равные времена
Скоростью равномерного прямолинейного движения
называется отношение перемещения точки ( Dr )
ко времени (Dt),
Dr2
за которое это перемещение произошло.
Из формулы видно, что
перемещение точки
Dr3
за время Dt.
направление вектора скорости v
в данном движении совпадает
с направлением вектора перемещения Dr
(поскольку число Dt > 0)
v Dr
v const
Вектор скорости направлен в ту сторону, в которую движется точка.
Dr
v
Dt
Если движение равномерно и прямолинейно,то с какого бы момента мы ни начали отсчет
промежутка времени Dt, перемещение D r , совершенное за это время,
будет одним и тем же. Значит, вектор скорости v Dr Dt будет одним и тем же
в любой момент равномерного прямолинейного движения.
Вектор скорости при равномерном прямолинейном движении не изменяется.

6.

VI. Равномерное прямолинейное движение.
Кинематическое уравнение движения
Кинематическими уравнениями движения называют формулы,
которые выражают зависимость координат движущейся точки от времени.
x(t) = …
y(t) = …
z(t) = …
Чтобы получить такие уравнения для равномерного прямолинейного движения
запишем формулу скорости в этом движении
в проекциях на ось ОХ:
Если отсчет времени начать с момента t1
(то есть в этот момент включить секундомер,
стрелка которого стоит на отметке «0»)
то получится, что t1 = 0
(таковы показания секундомера в этот момент)
Координату точки в момент t = 0 принято обозначать « x0 »
таким образом, в нашей формуле вместо x1 будем писать x0
Вместо t2 будем писать просто t (индекс «2» теряет смысл, т. к. величины t1
в формуле теперь нет)
Вместо x2 будем писать просто x (x — координата точки в момент t — конечная
vx t = x – x0
x = x0 + vxt
x0 — координата точки в момент t = 0
(начальная координата)
координата)

7.

VII. Графики равномерного движения
Зависимость модуля скорости от времени
v
В равномерном движении модуль скорости не меняется.
(v = const)
t
Значит, график v(t) не может подниматься вверх
(это означало бы увеличение скорости)
и не может опускаться вниз
(это означало бы уменьшение скорости).
График представляет собой прямую, параллельную оси t.
Вычислим площадь фигуры, заключенной между графиком v(t)
и участком оси t,
v
который соответствует некоторому промежутку времени Dt.
Искомая площадь равна площади прямоугольника
со сторонами v и Dt .
v
При равномерном движении
t произведение модуля скорости v на время движения Dt
Отсюда правило:
Dt
равно пройденному пути s.
Площадь, заключенная между графиком зависимости модуля скорости v
от времени t и осью Оt, численно равна пути, который пройден за тот промежуток
времени, над которым лежит эта площадь.
Sпод графиком v(t) = s
численно

8.

VIII. Графики равномерного движения
Зависимость проекции скорости от времени
В равномерном прямолинейном движении вектор скорости не изменяется,
vx значит, его проекции тоже остаются постоянными. (vx = const)
t
vx
Следовательно, график vx(t) не может подниматься вверх
и не может опускаться вниз.
График представляет собой прямую, параллельную оси t.
Вычислим площадь фигуры, заключенной между графиком vx(t)
и участком оси t, который соответствует некоторому промежутку времени Dt.
vx
Искомая площадь равна площади прямоугольника со сторонами vx и Dt .
При равномерном прямолинейном движении
произведение проекции скорости vx на время движения Dt
t
равно изменению координаты Dx.
(Это следует из формулы x = x0 + vxt vxt = x - x0 = Dx)
Dt
Отсюда правило:
Площадь, заключенная между графиком зависимости проекции скорости vx(t) и
осью Оt, численно равна изменению координаты, которое произошло за тот
промежуток времени, над (или под) которым лежит эта площадь.
Sмежду графиком vx(t) и осью Оt = Dx
численно
«+» — если площадь лежит выше оси Ot, «-» — если ниже.