Похожие презентации:
Кинематика. Основные задачи кинематики
1. ВВЕДЕНИЕ
Кинематика – раздел теоретической механики,в котором изучают движение материальных точек
и тел без учета причин, вызывающих или изменяющих это
движение (сил).
Основные задачи кинематики:
Установление математических способов задания
движения точек (тел).
Определение по заданному движению точки (тела), всех
кинематических характеристик этого движения:
траекторий, скоростей , ускорений, угловых скоростей,
угловых ускорений и т.д...
2. Свойства пространства и времени в классической механике
ПространствоВремя
однородно,
однонаправлено,
изотропно,
непрерывно,
геометрия
пространства –
евклидова.
протекает одинаково и
равномерно во всех
точках пространства и на
всех как угодно
движущихся телах.
Замечание. Указанные свойства пространства и времени приближенно
отражают их реальные свойства при движениях со скоростями V << c .
3. Система отсчета
Положение и движение точки (тела) впространстве относительны: их можно
определить только по отношению к другому
произвольно выбранному телу - телу отсчета.
Системой отсчета (СО) называют совокупность
тела отсчета и связанной с ним системы
координат и часов по отношению к которому
изучается движение данной точки (тела).
Характер движения точки (тела) существенно
зависит от выбора системы отсчета.
4.
Глава 1Кинематика точки
§ 1.1 Способы задания движения точки
Движение точки считается заданным, если известен способ, при
помощи которого можно однозначно определить положение
точки в пространстве в любой момент времени относительно
выбранной системы отсчета.
Существуют три способа задания движения точки:
1) векторный способ задания движения;
2) координатный способ задания движения;
3) естественный (траекторный) способ задания движения.
Траектория точки – есть геометрическое место точек
пространства, последовательно занимаемых движущейся
точкой.
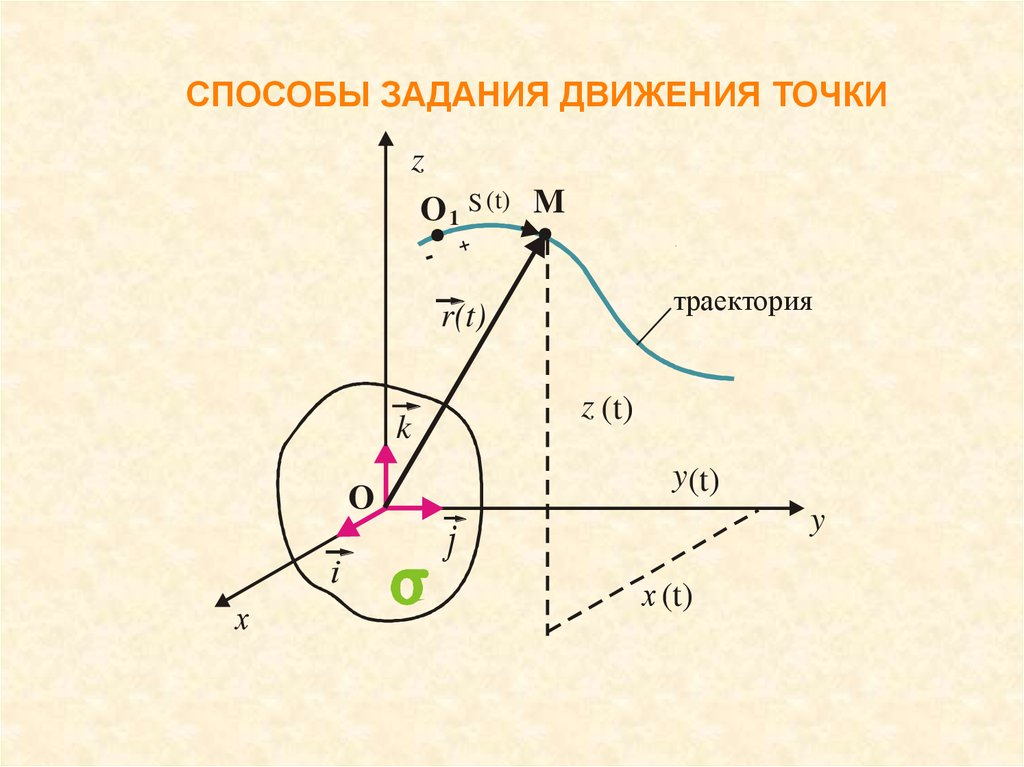
5. Способы задания движения точки
1) Векторный способ задания движения:задается система отсчета;
положение точки в пространстве определяется радиусомвектором r = r ( t ) , направленным из начала системы
отсчета в движущуюся точку.
Зависимость r = r ( t ) однозначная и непрерывная!
ЗАМЕЧАНИЕ! Вид системы координат при этом способе
задания движения произволен, поэтому векторный
способ задания движения используется для получения
основных кинематических характеристик движения точки.
6. Способы задания движения точки
2) координатный способ задания движения:задается система отсчета;
положение точки в пространстве определяется декартовыми
координатами:
x x t
y y t
z z t .
Зависимость координат от времени - однозначная и непрерывная.
Замечание. Помимо декартовых координат для задания
положения точки в пространстве можно использовать также
полярные, цилиндрические, сферические и произвольные
криволинейные координаты.
7. Способы задания движения точки
3) Естественный (траекторный) способ задания движения:задается система отсчета;
задается траектория точки;
на траектории задается начало отсчета и положительное
направление отсчета дуговой координаты s;
закон изменения дуговой координаты s = s(t) ;
Зависимость s = s(t) - однозначная и непрерывная!
8. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
zO 1 S (t) M
-
+
траектория
r(t)
k
O
z (t)
y(t)
y
(t)
9. § 1.2 СВЯЗЬ МЕЖДУ СПОСОБАМИ ЗАДАНИЯ ДВИЖЕНИЯ ТОЧКИ
Пусть движение точки задано координатным способом:x f1 (t ), y f 2 (t ), z f 3 (t ) (1).
Переход к векторному способу
задания движения точки.
z
r (t ) x(t )i y (t ) j z (t )k .
Переход к естественному способу
задания движения точки.
Траекторию точки можно найти,
исключая из уравнений движения (1)
время t : например
t f1( 1) ( x).
Тогда траектория точки есть линия
пересечения двух поверхностей
ds
dz
dx
.
dy
y
О
x
ds 2 dx 2 dy 2 dz 2
y f 2 ( f1( 1) ( x)) 0,
Ф1 ( x, y) 0,
2
2
2
2
или
(
x
y
z
)(
dt
)
.
( 1)
Ф
(
x
,
z
)
0.
z
f
(
f
(
x
))
0.
2
3
1
2
2
2
s
(
t
)
s
x
y
z
dt.
Закон движения точки по траектории:
0
Замечание. Параметр s0 и знак перед интегралом зависят от выбора начала
отсчета и положительного направления отсчета дуговой координаты.
10.
ГЛАВА 2.ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ
ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ ТОЧКИ
СКОРОСТЬ ТОЧКИ
Скорость точки V - векторная величина,
характеризующая быстроту и направление изменения
положения точки в пространстве относительно
выбранной системы отсчета с течением времени.
УСКОРЕНИЕ ТОЧКИ
Ускорение точки a - векторная величина,
характеризующая изменение вектора скорости точки
по модулю и по направлению.
11.
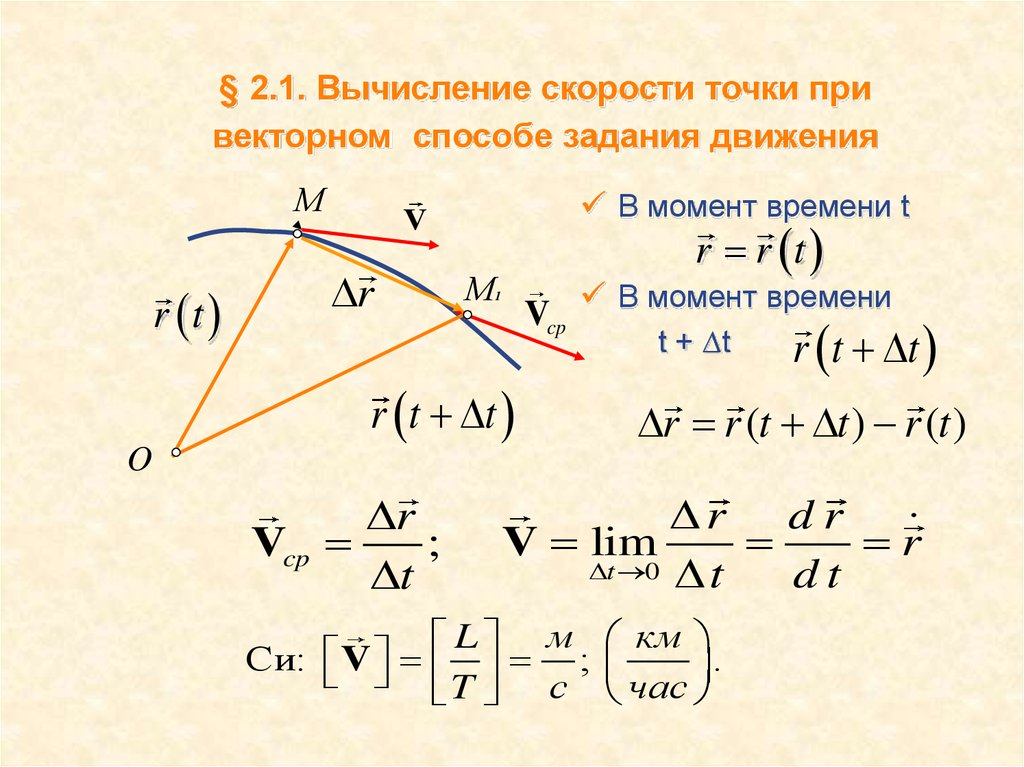
§ 2.1. Вычисление скорости точки привекторном способе задания движения
М
r t
В момент времени t
V
r
М
r r t
Vcp В момент времени
1
t + ∆t
r t t
r t t
r r (t t ) r (t )
O
r
Vcp
;
t
.
r d r
V lim
r
t 0 t
dt
L м км
Си: V ;
.
T с час
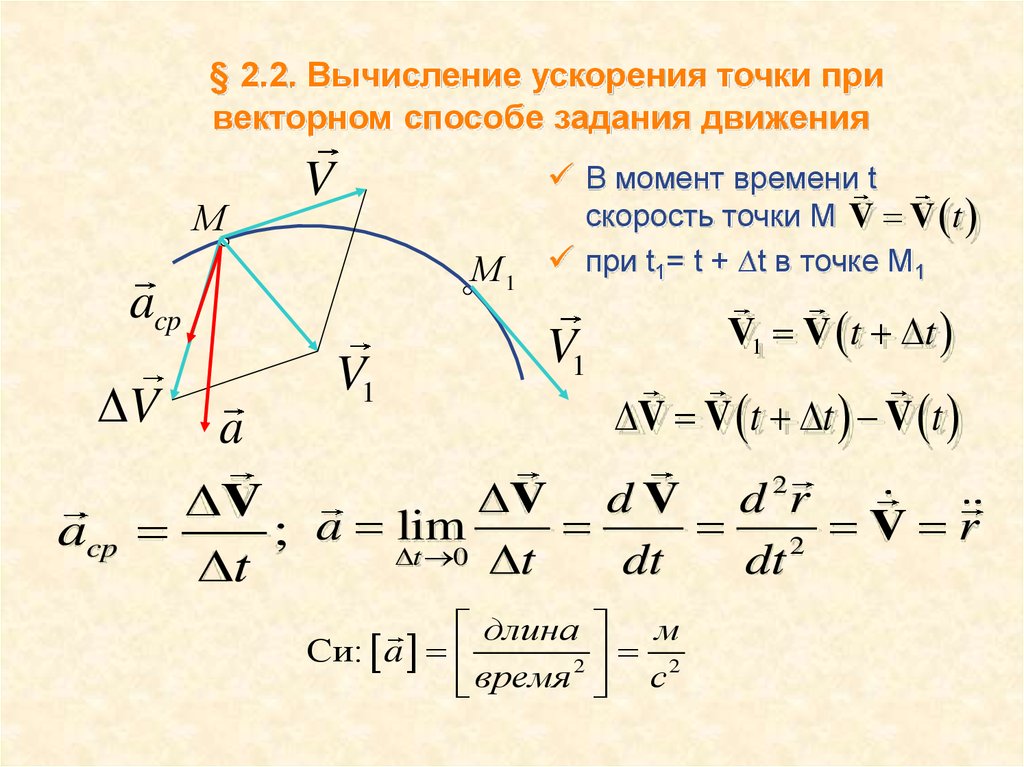
12. § 2.2. Вычисление ускорения точки при векторном способе задания движения
МV
М1
acp
V
V1
a
В момент времени t
скорость точки М V V t
при t1= t + ∆t в точке М1
V1
V1 V t t
V V t t V t
V d V d r
V
2 V r
; a lim
t 0 t
dt
dt
t
2
acp
длина м
Си: a
2
2
время с
13.
§ 2.3. Вычисление скорости точки прикоординатном способе задания движения
r xi y j z k
dr dx
dy
dz
V
i
j
k xi y j z k
dt d t
dt
dt
V Vx i Vy j Vz k
Vx x ,
V y y ,
Vz z .
V Vx2 Vy2 Vz2
,
Vy
cos V, y ,
V
V
cos V, z z
V
Vx
cos V, x
V
направляющ ие
косинусы
14. § 2.4. Вычисление ускорения точки при координатном способе задания движения
d Vyd V d Vx
d Vz
a
i
j
k
dt
dt
dt
dt
d 2r d 2 x
d2 y
d2 z
2 2 i 2 j 2 k
dt
dt
dt
dt
a ax i a y j az k
a x Vx x ,
a y Vy y ,
a z Vz z .
a ax2 a y2 az2
ax
cos a , x ,
a
a y
cos a , y ,
a
az
cos a , z .
a
направляющ ие
косинусы
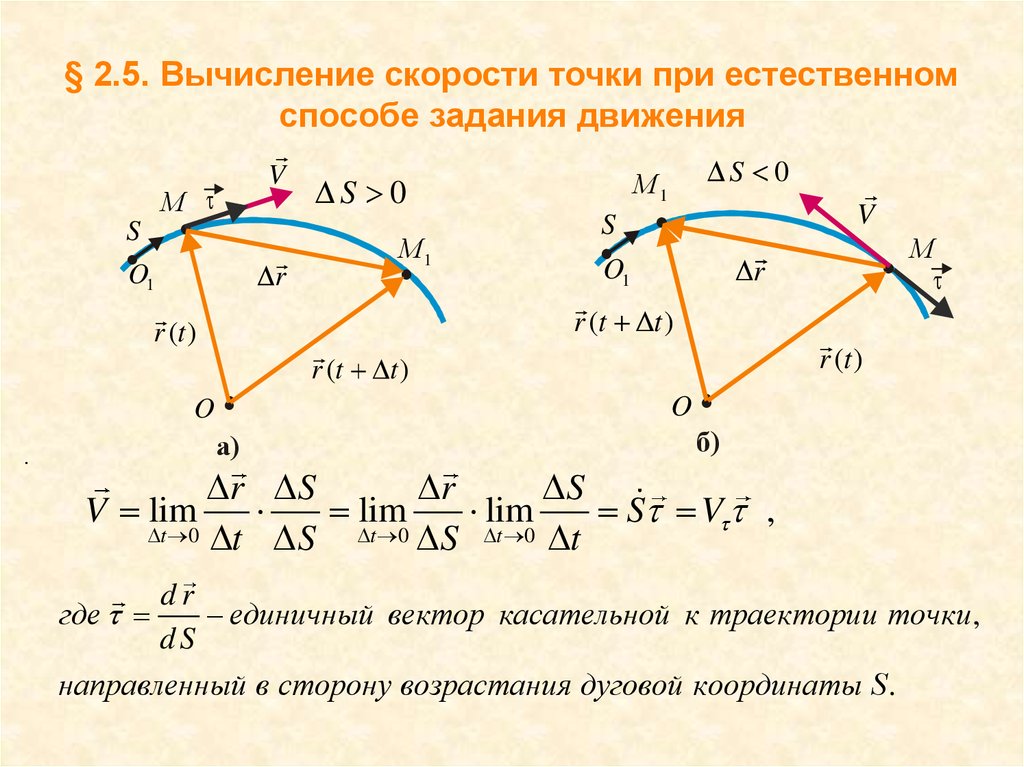
15. § 2.5. Вычисление скорости точки при естественном способе задания движения
МS
•O1
V
S
М1
r
.
O •
а)
S
•O1
r (t
r (t )
r (t
t)
S
М1
0
0
V
r
М
t)
r (t )
O •
б)
r S
r
S
V lim
lim
lim
S V ,
t 0 t S
t 0 S t 0 t
где
dr
единичный вектор касательной к траектории точки ,
dS
направленный в сторону возрастания дуговой координаты S .
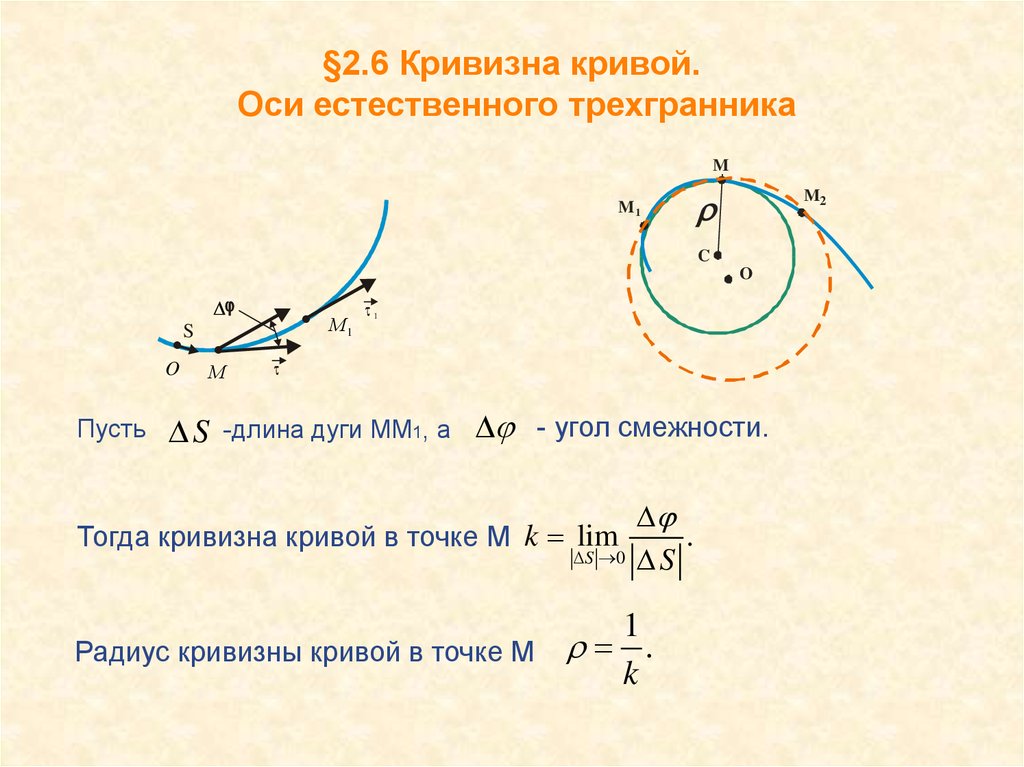
16. §2.6 Кривизна кривой. Оси естественного трехгранника
MM1
r
M2
C
O
S
•
O
М
Пусть
S
М1
1
-длина дуги ММ1, а
- угол смежности.
Тогда кривизна кривой в точке М k lim
S 0
.
S
1
Радиус кривизны кривой в точке М r .
k
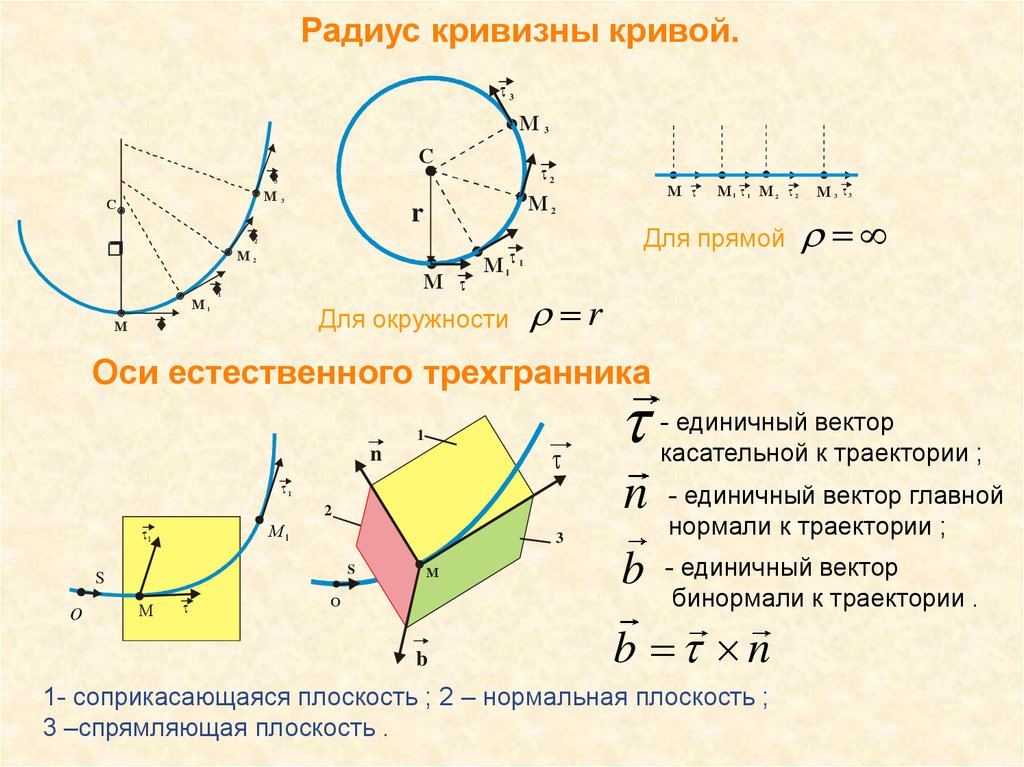
17. Радиус кривизны кривой.
3М3
С
2
М2
t3
М3
С
r
t2
r
М2
М1
М
t1
М1 1 М 2 2
Для прямой
М 1
М 3 3
r
1
Для окружности
t
М
М
r r
Оси естественного трехгранника
1
n
1
2
М1
1
O
М
S
М
О
b
- единичный вектор
касательной к траектории ;
n
- единичный вектор главной
нормали к траектории ;
b
- единичный вектор
бинормали к траектории .
3
S
b n
1- соприкасающаяся плоскость ; 2 – нормальная плоскость ;
3 –спрямляющая плоскость .
18. § 2.7 Вычисление ускорения точки при естественном способе задания движения
B1
•М
1
1
dV d (V ) dV
dV
V 2
d
a
V
n
dt
dt
dt
dt
dt
r
S
d
lim
lim
t
0
t
0
dt
t
t S
1
S
V lim
lim
lim
lim
0
A
t 0 t t 0 S t 0
М
r t 0
sin
2 1.
Из АМВ : 2 sin
; тогда lim
lim
t 0
t 0
2
2
d ( )
d
d
Очевидно 1, поэтому
2
0, следовательно
.
d
d
d
S
•
M
Вектор лежит в соприкасающейся плоскости и
направлен в сторону вогнутости траектории.
Вывод : вектор
d
d
n.
19. Вычисление ускорения точки при естественном способе задания движения
a a an n abb2
dV d S касательное (тангенциальное)
2 ускорение
dt
dt
V 2
an
нормальное ускорение
r
a
ab 0
В каждый момент времени вектор ускорения
точки лежит в соприкасающейся плоскости!
a
n
an
a
M
a a 2 an2
Касательное ускорение характеризует изменение модуля вектора
скорости точки.
a 0
a 0
при движении точки с постоянной скоростью;
в моменты времени, когда скорость точки достигает экстремальных значений
Нормальное ускорение характеризует изменение направления вектора
скорости точки.
an 0
an 0
при движении точки по прямой;
в моменты времени, когда скорость точки
а также в точках перегиба траектории.
V 0,
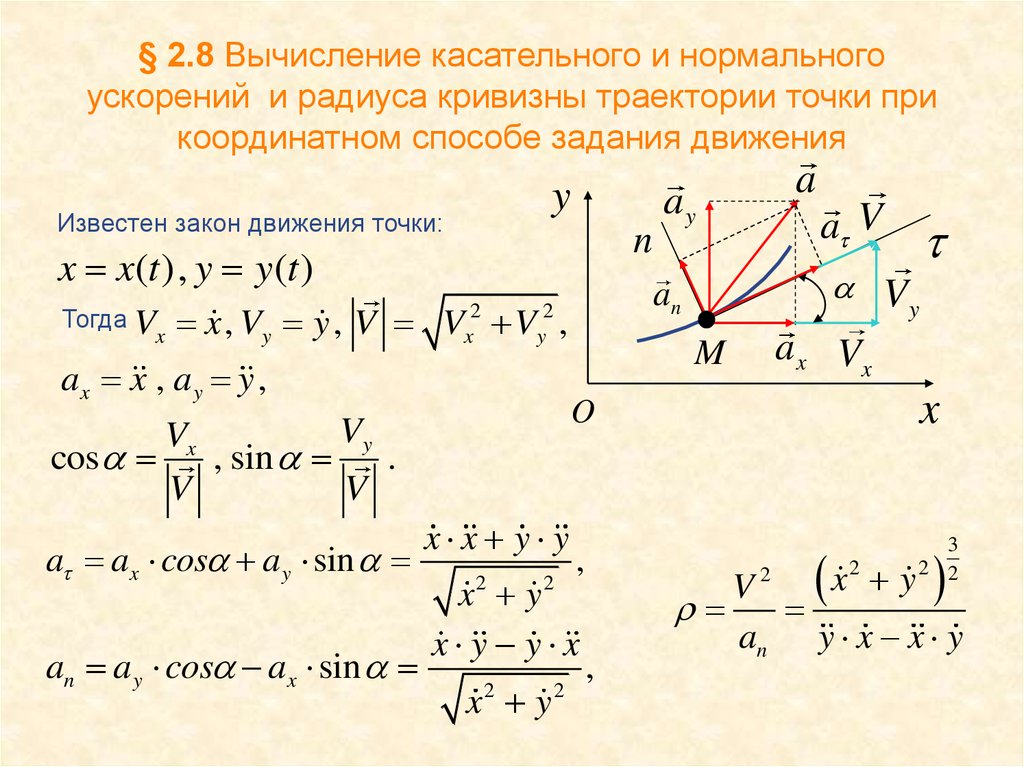
20. § 2.8 Вычисление касательного и нормального ускорений и радиуса кривизны траектории точки при координатном способе задания
движенияy
Известен закон движения точки:
n
x x(t ), y y(t )
Тогда V
x
an
x , Vy y , V V V ,
2
x
2
y
ax x , a y y ,
Vy
Vx
cos
, sin
.
V
V
a ax cos a y sin
an a y cos ax sin
x x y y
2
x y
2
2
a V
V
y
a x Vx
M
O
x
,
3
2 2
x y
x y y x
2
a
ay
V
r
an y x x y
2
,
2
x
y
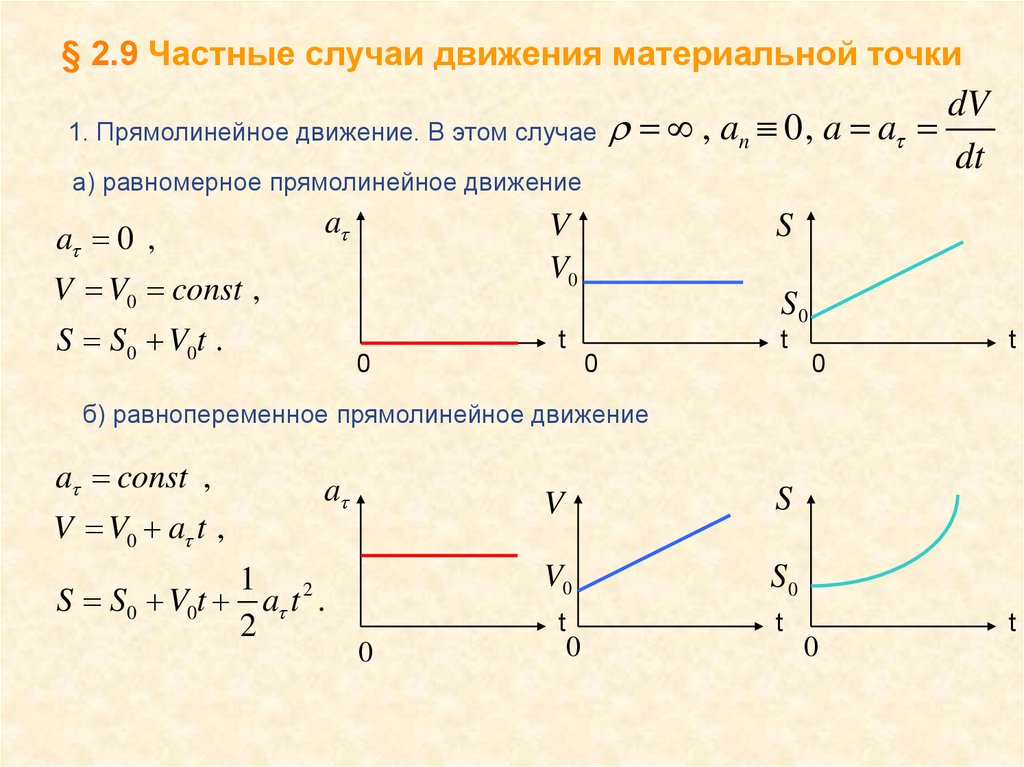
21. § 2.9 Частные случаи движения материальной точки
1. Прямолинейное движение. В этом случаеа) равномерное прямолинейное движение
a 0 ,
a
dV
r , an 0, a a
dt
V
V0
V V0 const ,
S
S0
S S0 V0t .
t
t
0
0
t
0
б) равнопеременное прямолинейное движение
a const ,
V V0 a t ,
a
1 2
S S0 V0t a t .
2
0
V
S
V0
S0
t
t
0
0
t
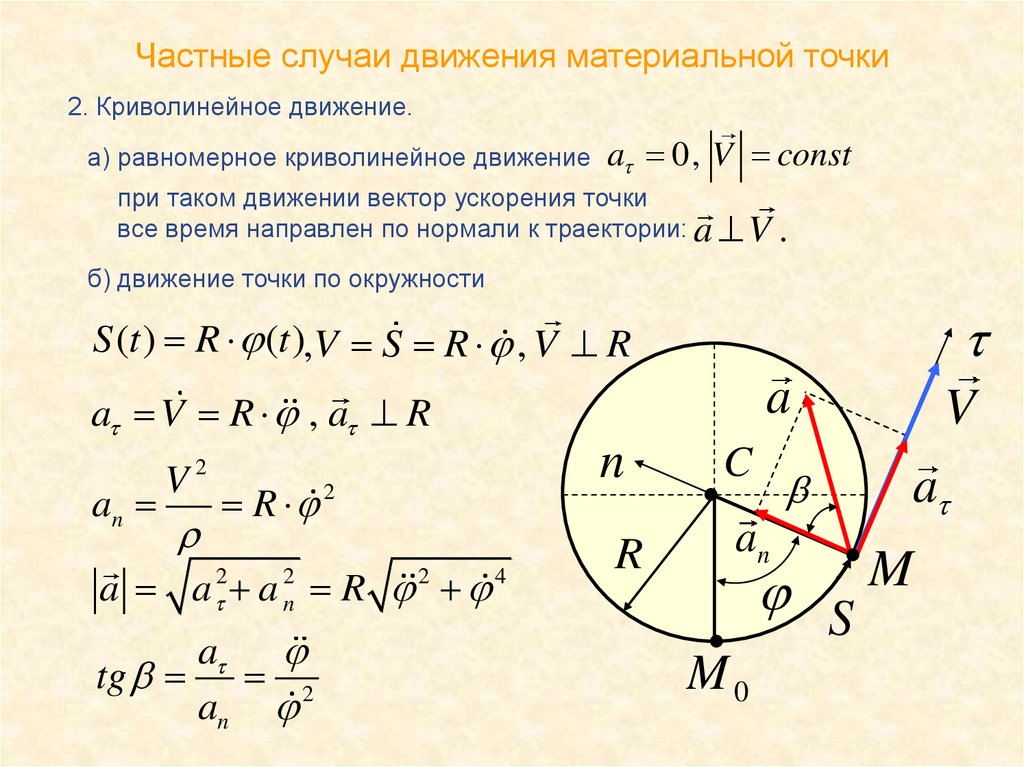
22. Частные случаи движения материальной точки
2. Криволинейное движение.а) равномерное криволинейное движение
a 0, V const
при таком движении вектор ускорения точки
все время направлен по нормали к траектории: a V .
б) движение точки по окружности
S (t ) R (t ),V S R , V R
a
a V R , a R
an
V2
r
R 2
a a 2 a 2n R 2 4
a
tg 2
an
n
R
.
a
.
M
S
.M
C
an
0
V













 Физика
Физика








