Похожие презентации:
Основные понятия кинематики. Кинематика точки
1. Основные понятия кинематики. Кинематика точки
ОСНОВНЫЕ ПОНЯТИЯКИНЕМАТИКИ.
КИНЕМАТИКА ТОЧКИ
Лекция 9
2. Основные кинематические параметры
ОСНОВНЫЕ КИНЕМАТИЧЕСКИЕ ПАРАМЕТРЫТраектория - линия, которую
очерчивает материальная точка при
движении в пространстве.
Траектория может быть прямой и
кривой, плоской и пространственной
линией.
Уравнение траектории при плоском
движении:
у = f(x).
Пройденный путь - измеряется вдоль
траектории в направлении движений.
обозначение — S,
единицы измерения — метры.
О
S
3. Уравнение движения точки - уравнение, определяющее положение движущейся точки в зависимости от времени
УРАВНЕНИЕ ДВИЖЕНИЯ ТОЧКИ - УРАВНЕНИЕ, ОПРЕДЕЛЯЮЩЕЕПОЛОЖЕНИЕ ДВИЖУЩЕЙСЯ ТОЧКИ В ЗАВИСИМОСТИ ОТ ВРЕМЕНИ
Положение точки в каждый момент времени
можно определить по расстоянию, пройденному
вдоль траектории от некоторой неподвижной
точки, рассматриваемой как начало отсчета.
Такой способ задания движения называется
естественным.
Таким образом, уравнение движения можно
представить в виде
S= f(t).
4. Уравнение движения точки - уравнение, определяющее положение движущейся точки в зависимости от времени
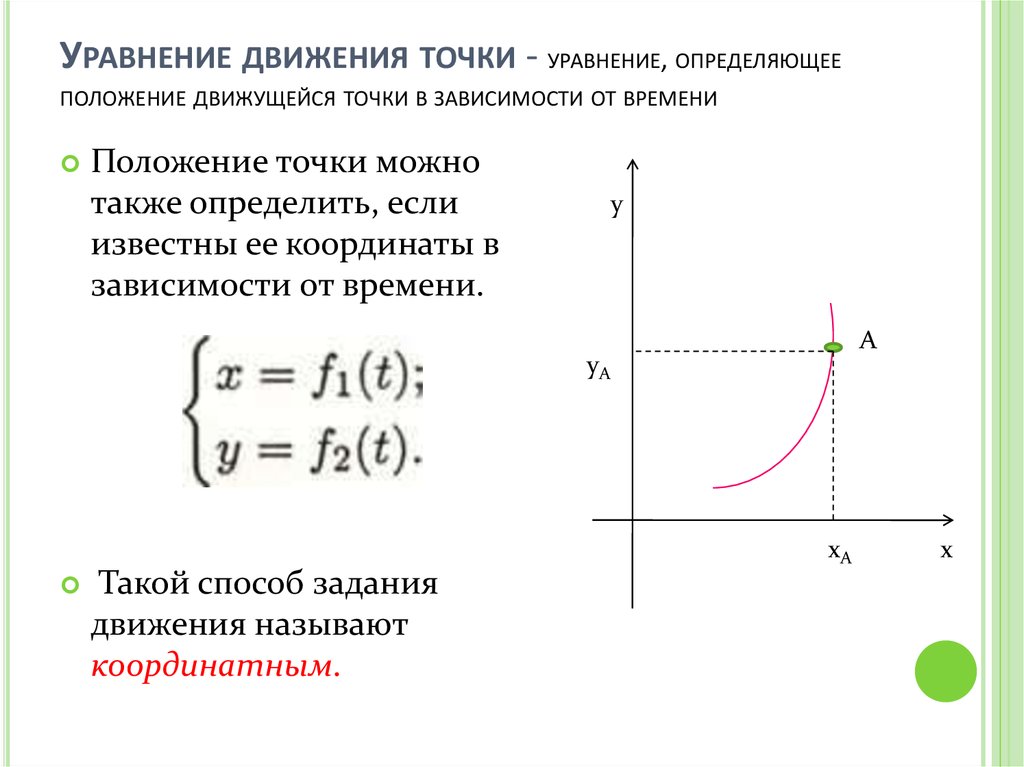
УРАВНЕНИЕ ДВИЖЕНИЯ ТОЧКИ - УРАВНЕНИЕ, ОПРЕДЕЛЯЮЩЕЕПОЛОЖЕНИЕ ДВИЖУЩЕЙСЯ ТОЧКИ В ЗАВИСИМОСТИ ОТ ВРЕМЕНИ
Положение точки можно
также определить, если
известны ее координаты в
зависимости от времени.
y
A
yA
Такой способ задания
движения называют
координатным.
xA
x
5. Скорость движения - векторная величина, характеризующая в данный момент быстроту и направление движения по траектории
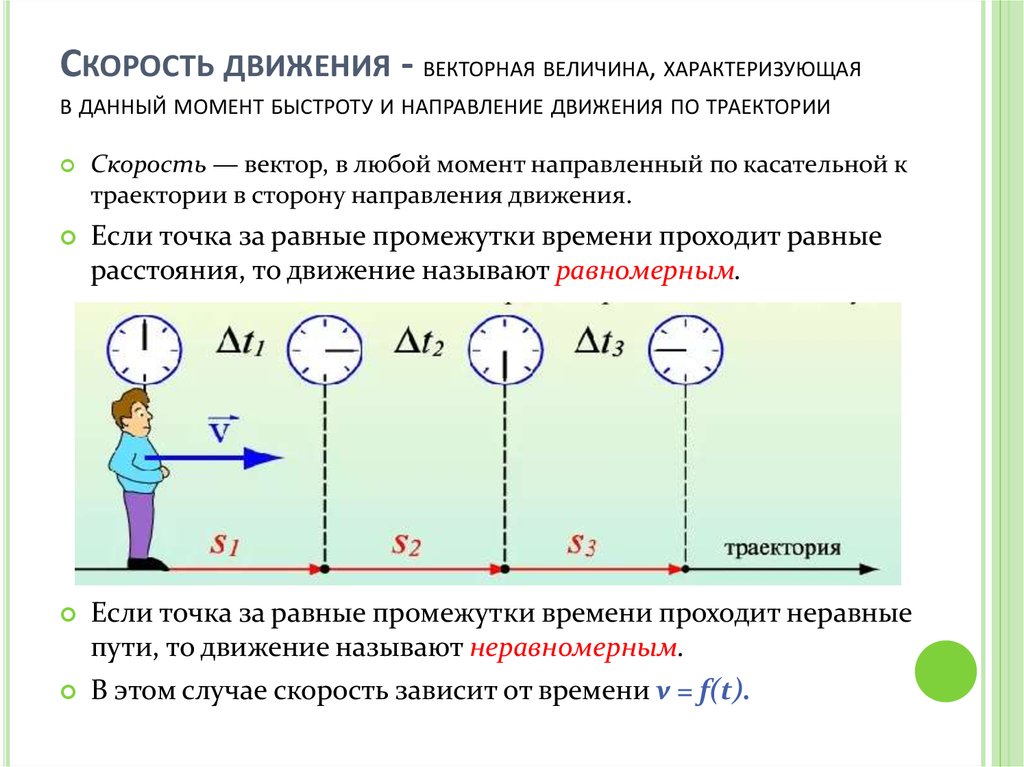
СКОРОСТЬ ДВИЖЕНИЯ - ВЕКТОРНАЯ ВЕЛИЧИНА, ХАРАКТЕРИЗУЮЩАЯВ ДАННЫЙ МОМЕНТ БЫСТРОТУ И НАПРАВЛЕНИЕ ДВИЖЕНИЯ ПО ТРАЕКТОРИИ
Скорость — вектор, в любой момент направленный по касательной к
траектории в сторону направления движения.
Если точка за равные промежутки времени проходит равные
расстояния, то движение называют равномерным.
Если точка за равные промежутки времени проходит неравные
пути, то движение называют неравномерным.
В этом случае скорость зависит от времени v = f(t).
6. Скорость движения - векторная величина, характеризующая в данный момент быстроту и направление движения по траектории
СКОРОСТЬ ДВИЖЕНИЯ - ВЕКТОРНАЯ ВЕЛИЧИНА, ХАРАКТЕРИЗУЮЩАЯВ ДАННЫЙ МОМЕНТ БЫСТРОТУ И НАПРАВЛЕНИЕ ДВИЖЕНИЯ ПО ТРАЕКТОРИИ
Средняя скорость на пути ΔS
S
t
При рассмотрении малых
промежутков времени (Δt 0)
средняя скорость становится
равной истинной скорости
движения в данный момент.
Поэтому скорость в данный момент
определяют как
Vср
dS
V
dt
V
7. Ускорение точки - векторная величина, характеризующая быстроту изменения скорости по величине и направлению
УСКОРЕНИЕ ТОЧКИ - ВЕКТОРНАЯ ВЕЛИЧИНА, ХАРАКТЕРИЗУЮЩАЯБЫСТРОТУ ИЗМЕНЕНИЯ СКОРОСТИ ПО ВЕЛИЧИНЕ И НАПРАВЛЕНИЮ
Скорость точки при
перемещении из точки М1 в
точку М2 меняется по
величине и направлению.
Среднее значение ускорения за
этот промежуток времени
V
аср
t
При рассмотрении бесконечно
малого промежутка времени
среднее ускорение превратится
в ускорение в данный момент:
dV
а
dt
8. Ускорение точки - векторная величина, характеризующая быстроту изменения скорости по величине и направлению
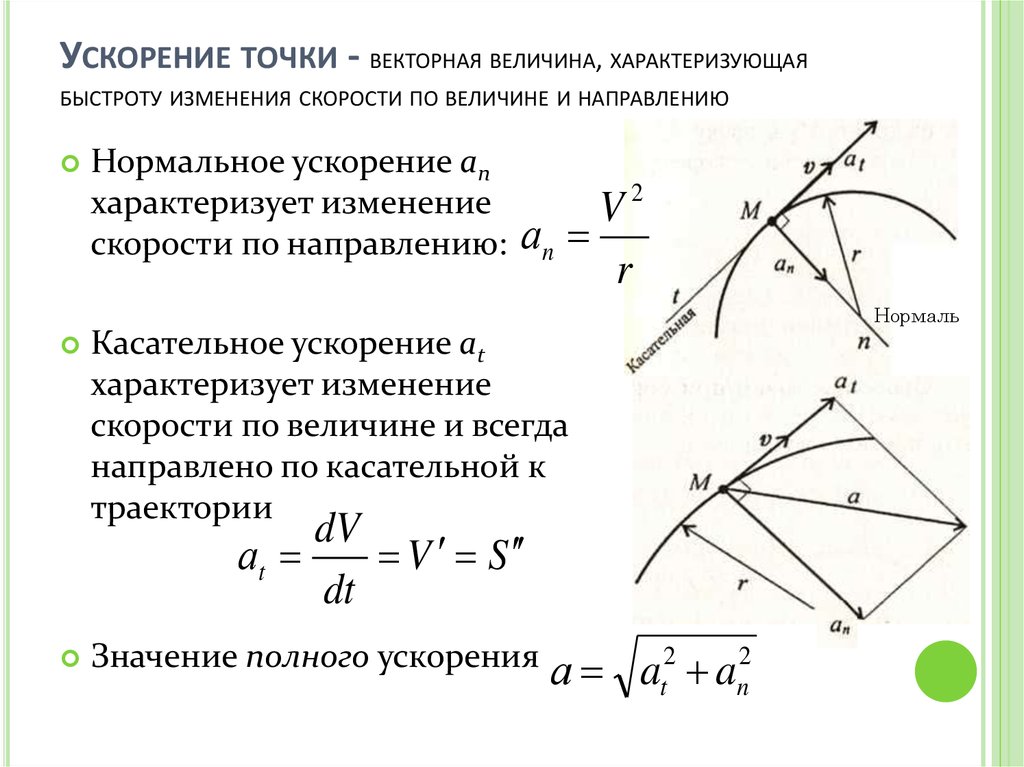
УСКОРЕНИЕ ТОЧКИ - ВЕКТОРНАЯ ВЕЛИЧИНА, ХАРАКТЕРИЗУЮЩАЯБЫСТРОТУ ИЗМЕНЕНИЯ СКОРОСТИ ПО ВЕЛИЧИНЕ И НАПРАВЛЕНИЮ
Нормальное ускорение ап
характеризует изменение
скорости по направлению:
V2
аn
r
Нормаль
Касательное ускорение at
характеризует изменение
скорости по величине и всегда
направлено по касательной к
траектории
dV
аt
V S
dt
Значение полного ускорения
а a a
2
t
2
n
9. Анализ видов и кинетических параметров движений
АНАЛИЗ ВИДОВ И КИНЕТИЧЕСКИХ ПАРАМЕТРОВ ДВИЖЕНИЙРавномерное движение — это движение с постоянной
скоростью: V = const
Прямолинейное
равномерное движение
Криволинейное
равномерное движение
dV
аt
at 0
dt
V2
r an
0
r
а
dV
at 0
dt
V2
r an
0
r
аt
at2 an2 0
а
at2 an2 an
Уравнение (закон) движения точки при равномерном движении
в общем виде является уравнением прямой:
S = So+Vt,
где So — путь, пройденный до начала отсчета
10. Анализ видов и кинетических параметров движений
АНАЛИЗ ВИДОВ И КИНЕТИЧЕСКИХ ПАРАМЕТРОВ ДВИЖЕНИЙРавнопеременное движение — это движение с
постоянным касательным ускорением: at = const
Прямолинейное
равнопеременное движение
at
аt const 0
r an
а
Криволинейное
равнопеременное движение
2
V
0
r
at2 an2 at
аt const 0
V2
r an
0
r
а
at2 an2
Значение скорости при равнопеременном движении
V V0 at t
Уравнение (закон) движения точки при равнопеременном движении
в общем виде является уравнением параболы:
at t 2
S S 0 V0 t
2
11. Кинематические графики — это графики изменения пути, скорости и ускорений в зависимости от времени
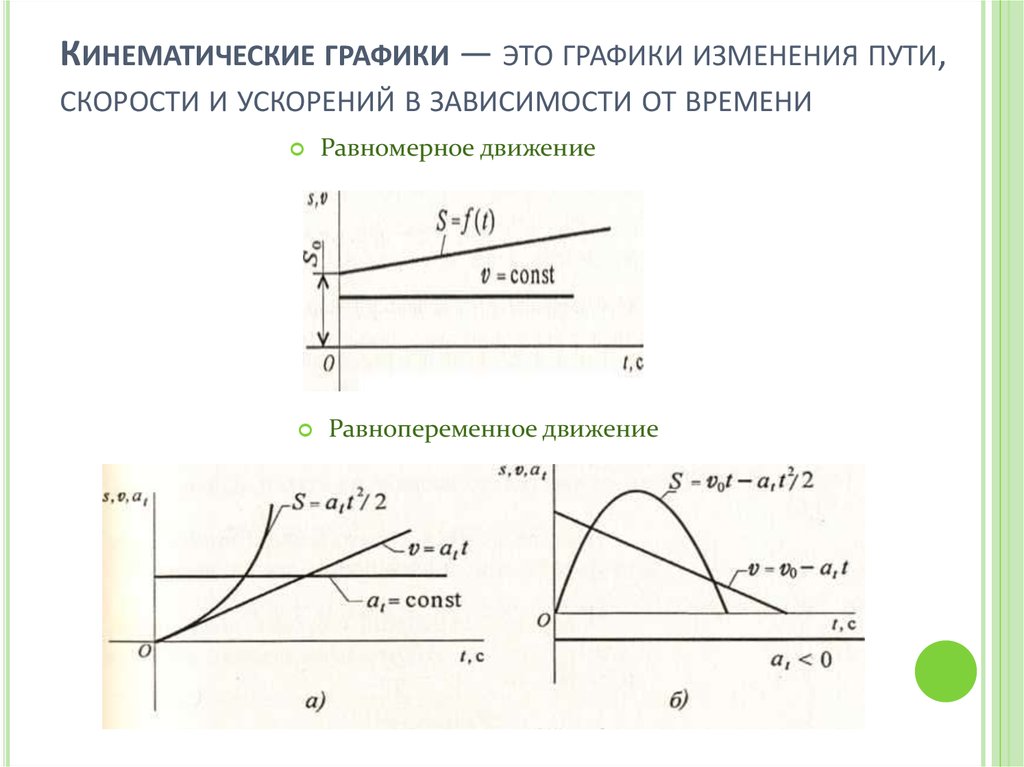
КИНЕМАТИЧЕСКИЕ ГРАФИКИ — ЭТО ГРАФИКИ ИЗМЕНЕНИЯ ПУТИ,СКОРОСТИ И УСКОРЕНИЙ В ЗАВИСИМОСТИ ОТ ВРЕМЕНИ
Равномерное движение
Равнопеременное движение
12.
13. Простейшие движения твердого тела
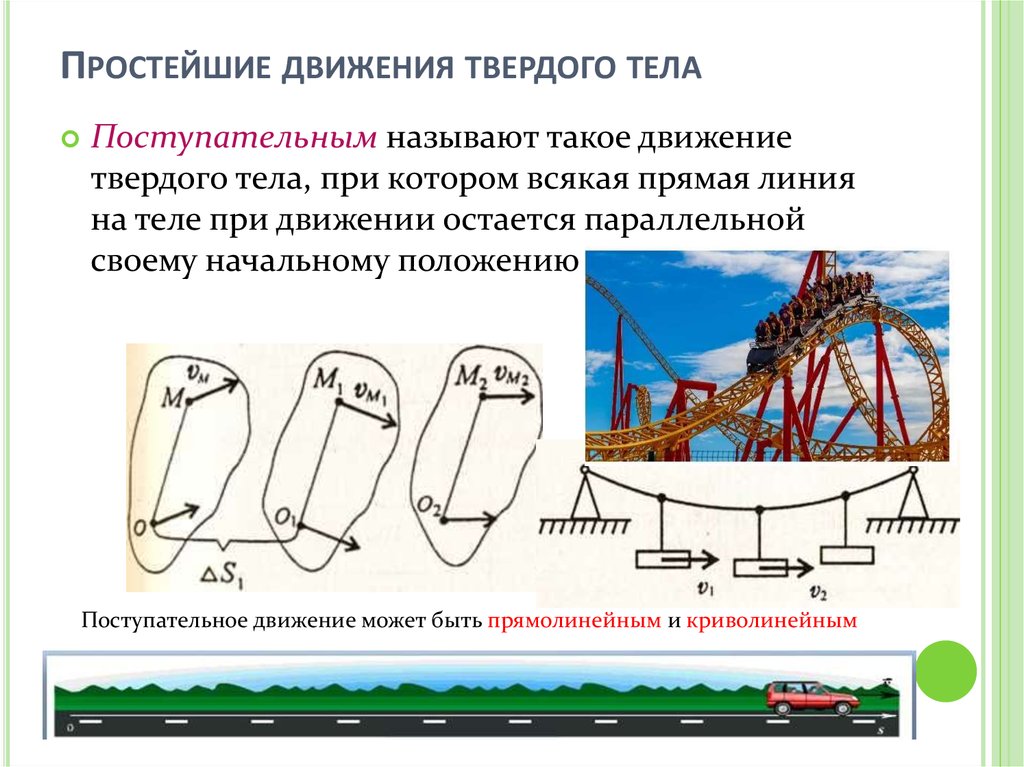
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛАПоступательным называют такое движение
твердого тела, при котором всякая прямая линия
на теле при движении остается параллельной
своему начальному положению
Поступательное движение может быть прямолинейным и криволинейным
14. Простейшие движения твердого тела
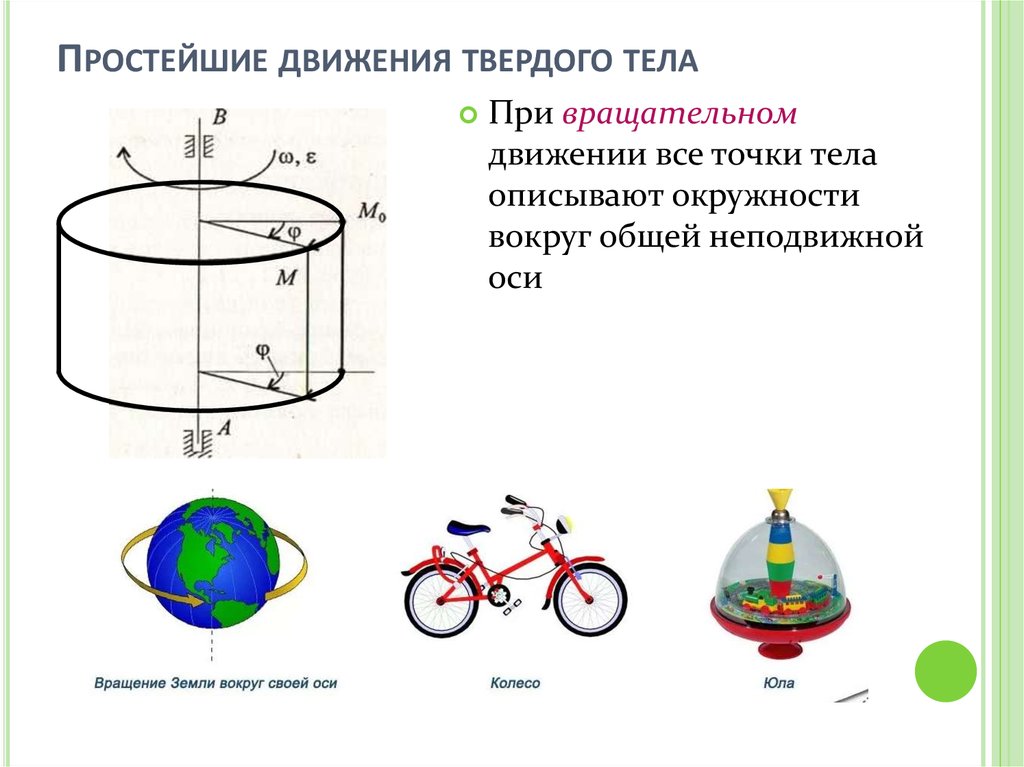
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛАПри вращательном
движении все точки тела
описывают окружности
вокруг общей неподвижной
оси
15. Простейшие движения твердого тела
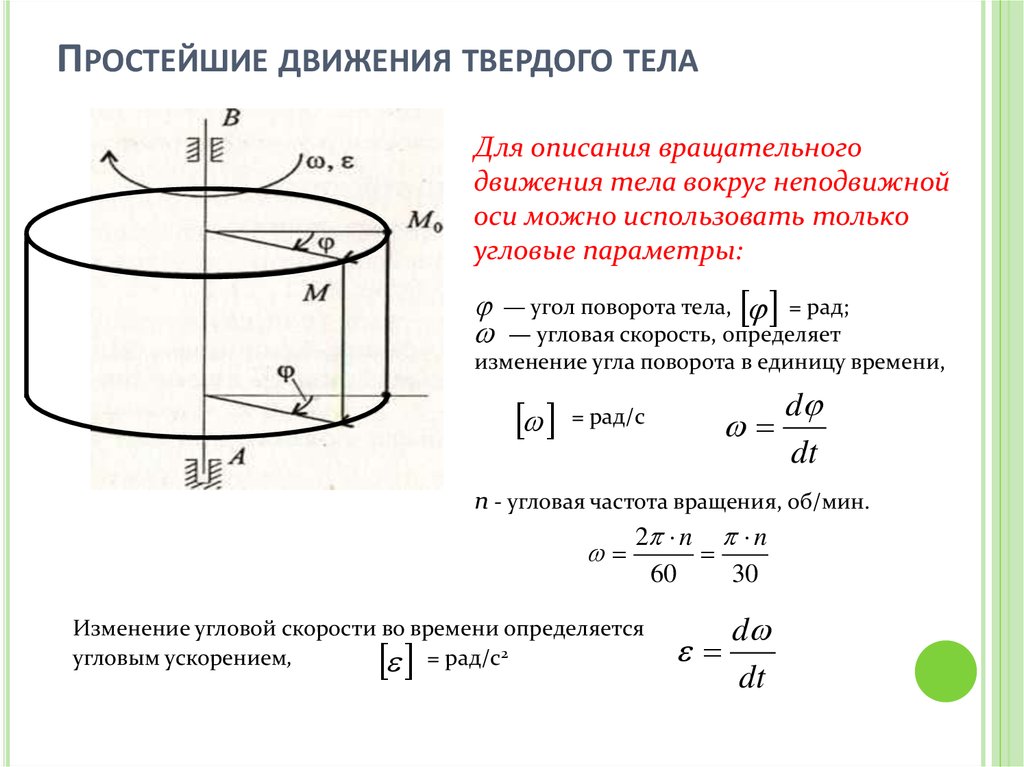
ПРОСТЕЙШИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛАДля описания вращательного
движения тела вокруг неподвижной
оси можно использовать только
угловые параметры:
— угол поворота тела, = рад;
— угловая скорость, определяет
изменение угла поворота в единицу времени,
= рад/с
d
dt
n - угловая частота вращения, об/мин.
2 n n
60
30
Изменение угловой скорости во времени определяется
угловым ускорением,
= рад/с2
d
dt
16. Частные случаи вращательного движения
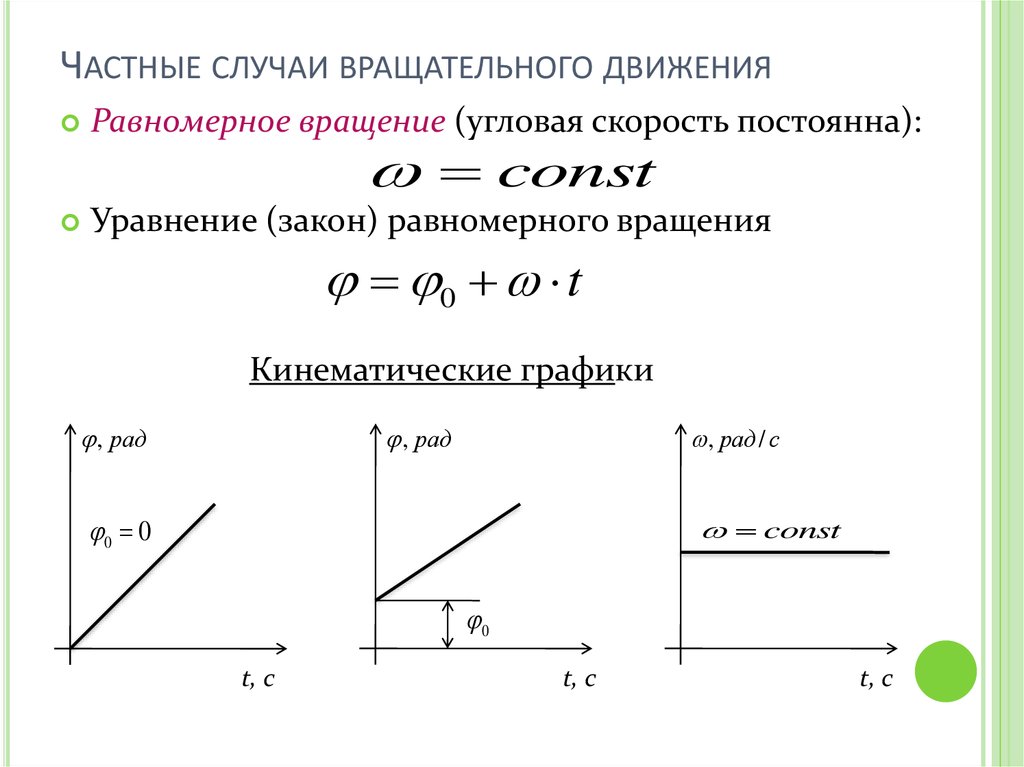
ЧАСТНЫЕ СЛУЧАИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯРавномерное вращение (угловая скорость постоянна):
Уравнение (закон) равномерного вращения
const
0 t
Кинематические графики
, рад
, рад
, рад / с
0 0
const
0
t, c
t, c
t, c
17. Частные случаи вращательного движения
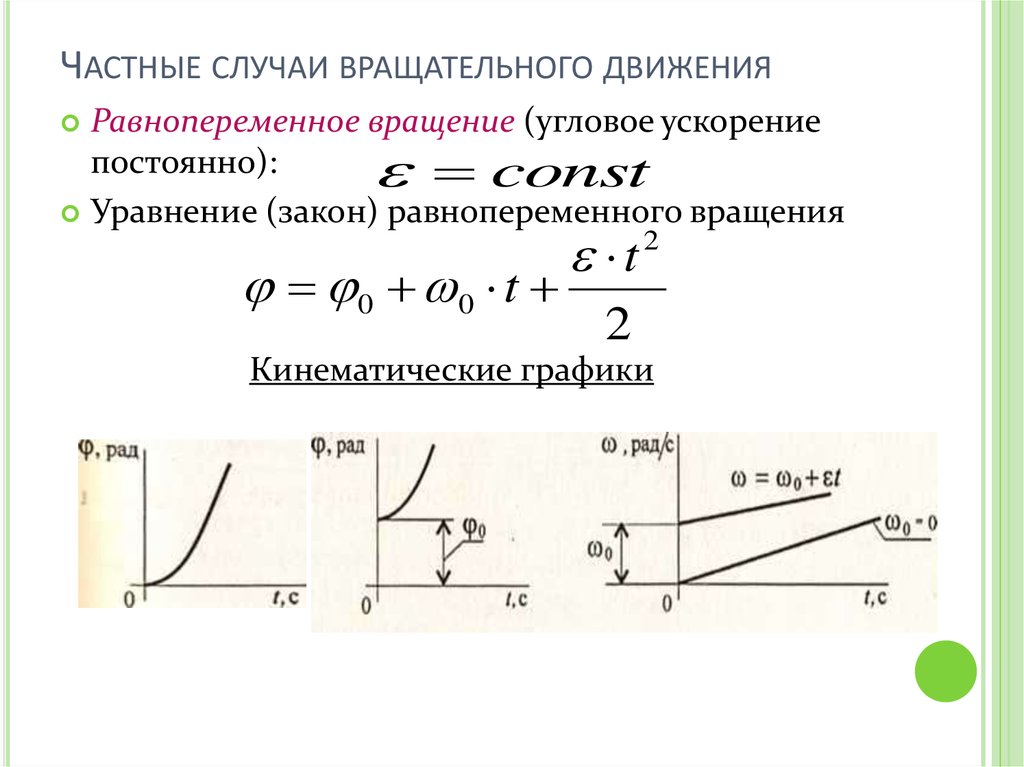
ЧАСТНЫЕ СЛУЧАИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯРавнопеременное вращение (угловое ускорение
постоянно):
const
Уравнение (закон) равнопеременного вращения
0 0 t
t2
2
Кинематические графики
18. Скорости и ускорения точек вращающегося тела
СКОРОСТИ И УСКОРЕНИЯ ТОЧЕК ВРАЩАЮЩЕГОСЯ ТЕЛАS A rA
Путь точки A:
Линейная скорость точки A:
VA rA
Ускорения точки А:
касательное
нормальное
atA rA
anA 2 rA
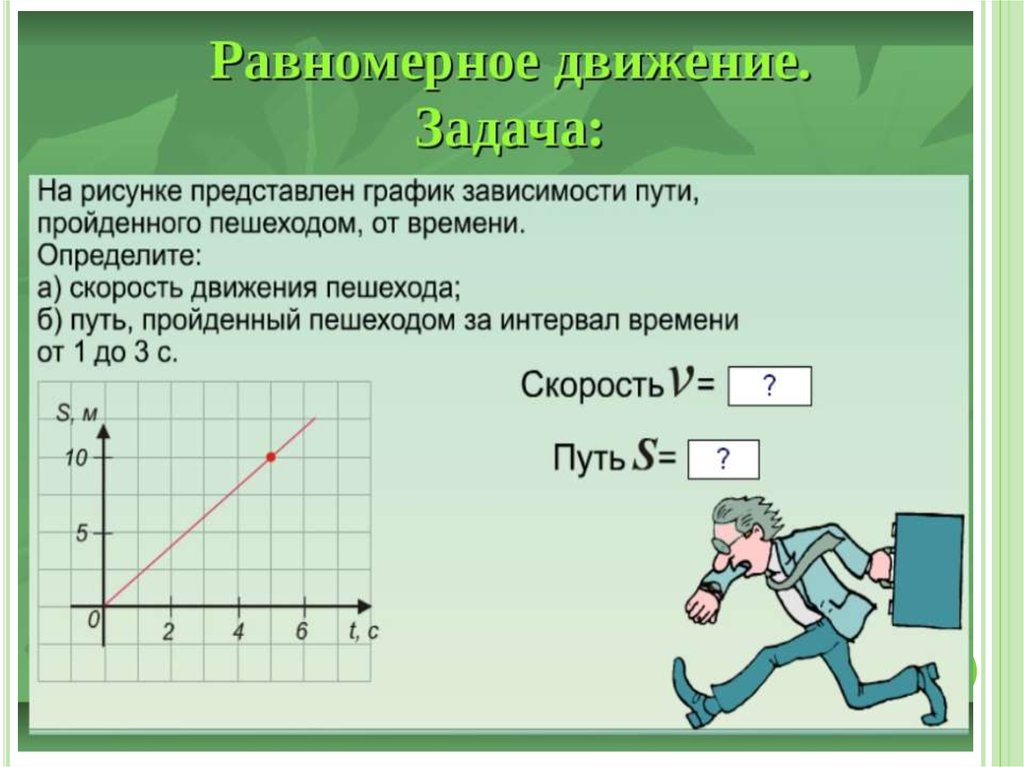
19. Примеры решения задач
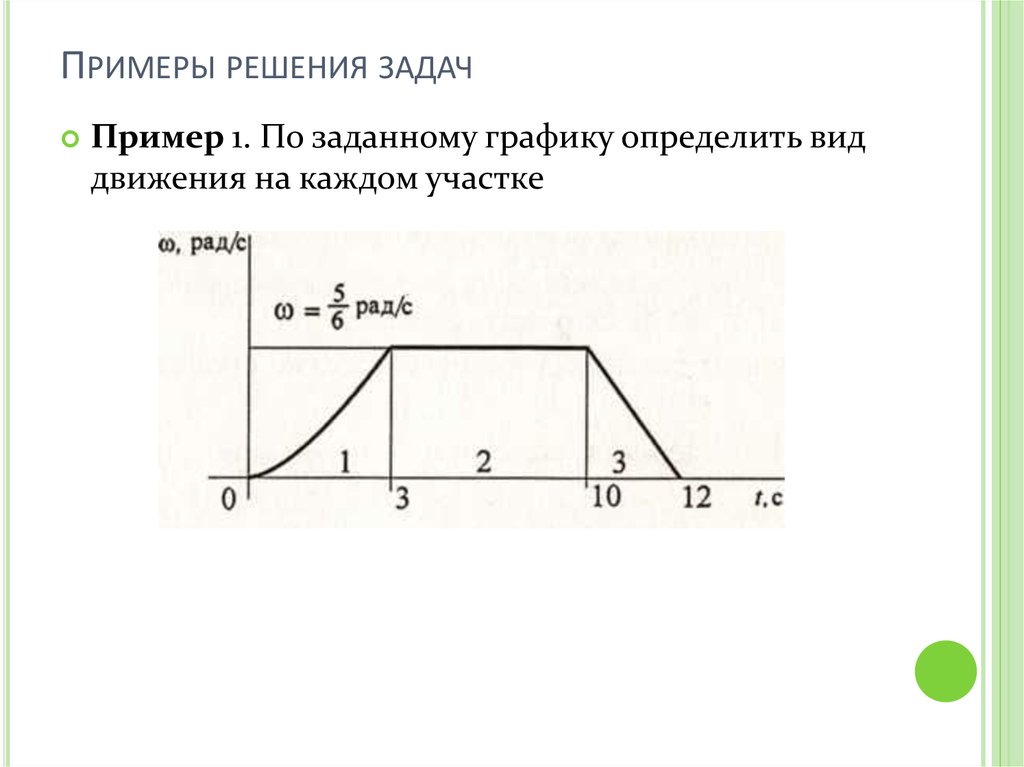
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧПример 1. По заданному графику определить вид
движения на каждом участке








 Физика
Физика








