Кинематика. Основные понятия

1.

2. К И Н Е М А Т И К А

КИНЕМАТИКА
Основные понятия:
система отсчета ( С О ),
cистема координат ( СК ),
материальная точка ( МТ ),
радиус-вектор, координаты,
вектор перемещения,
пройденный путь, скорость,
ускорение, кинематические
уравнения движения.

3. Различают движения

Прямолинейное,
криволинейное – по типу
траектории.
Равномерное ,
неравномерное,
равнопеременное – по виду
кинематических уравнений.

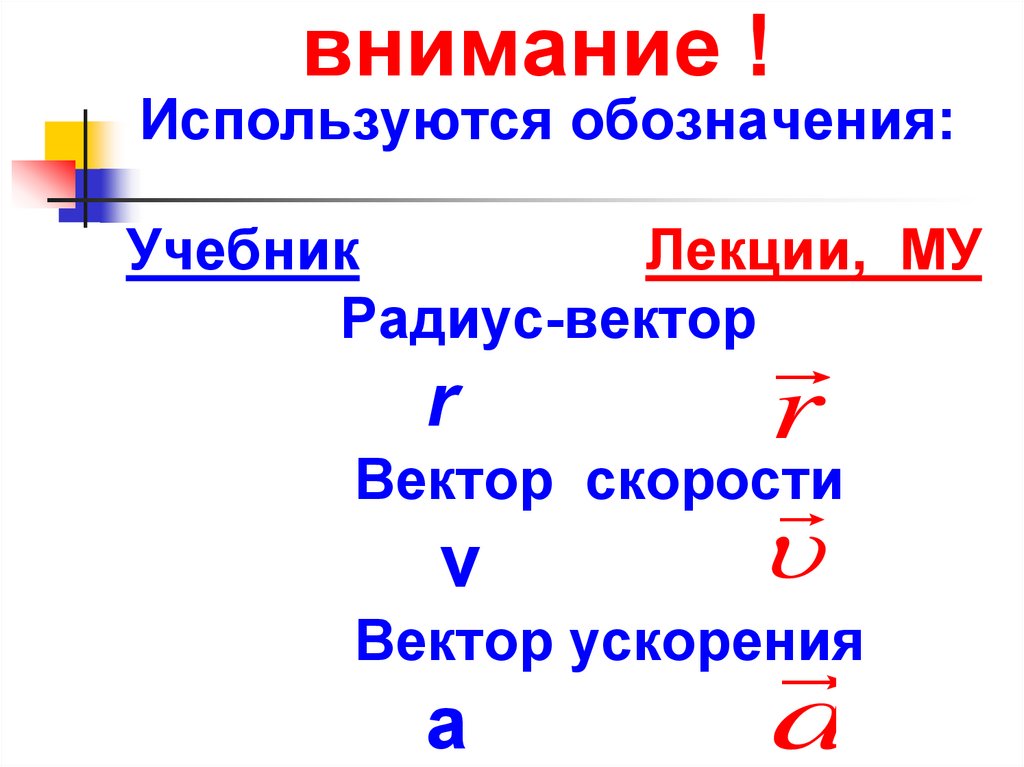
4. внимание !

Используются обозначения:
Учебник
Лекции, МУ
Радиус-вектор
r
Вектор
v
r
скорости
a
Вектор ускорения
а

5.

CО = СК + ТО + часы
Система отсчета определяет
положение тела в любой момент
времени.
Системы координат:
1)
2)
3)
4)
прямоугольная (декартовая);
полярная;
цилиндрическая;
сферическая.

6.

Прямоугольная (декартовая) СК
Z - аппликата

7.

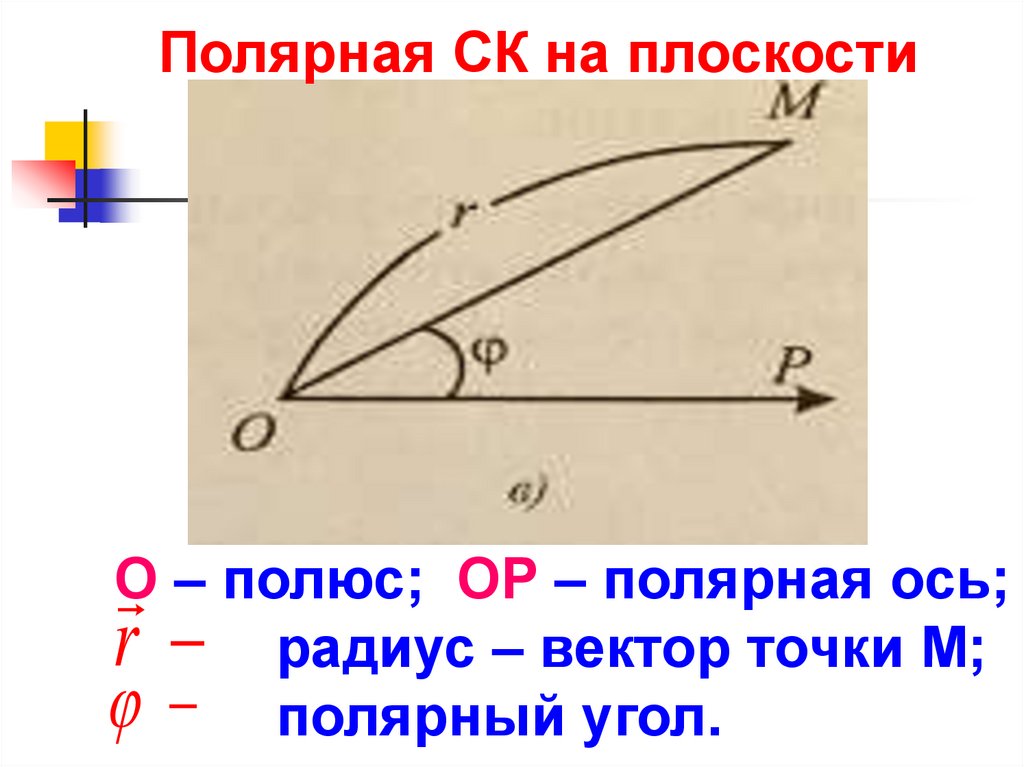
Полярная СК на плоскости
О
– полюс; ОР – полярная ось;
r радиус – вектор точки М;
полярный угол.

8.

- аналог полярных координат в
пространстве

9.

Определение положения точки с
помощью
координат
x,
y,
z
и
радиус-вектора r .

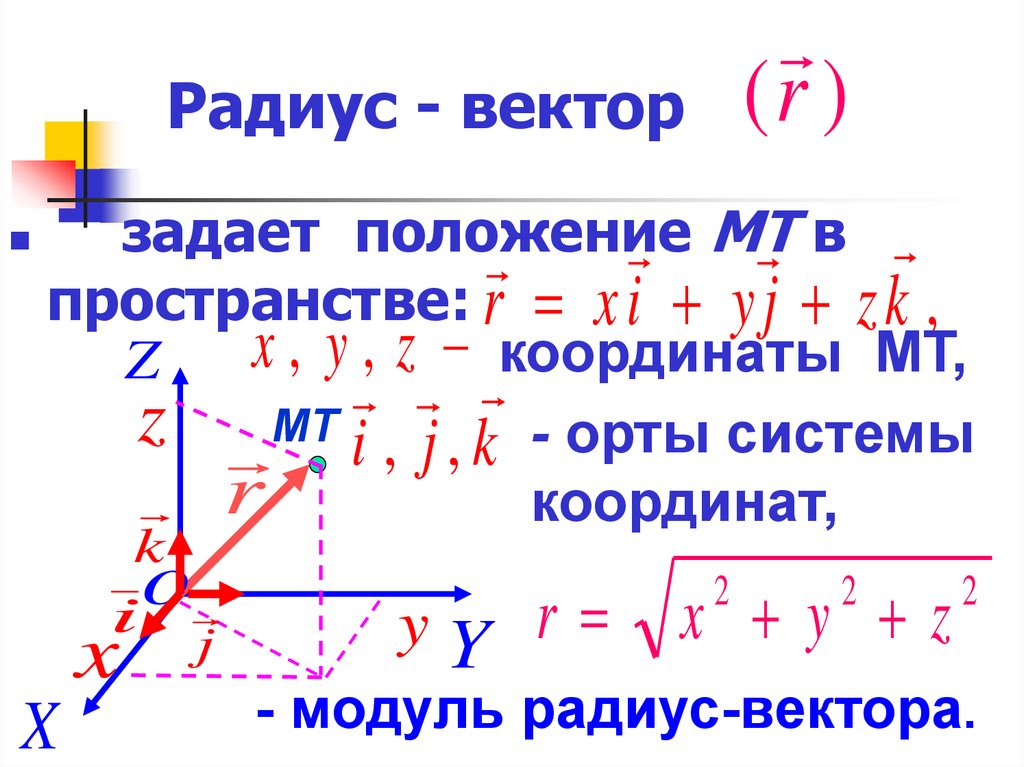
10. Радиус - вектор

(r )
Радиус - вектор
задает положение
МТ
в
пространстве: r x i y j z k ,
x , y , z координаты МТ,
Z
z МТ i , j , k - орты системы
r
координат,
k
o
i
x
X
j
yY r
x y z
2
2
2
- модуль радиус-вектора.

11.

Z
o
X
Вектор перемещения r
и пройденный путь s
r
r
r
2
1
t
- вектор перемещения,
путь,
s
s
r1
пройденный за
r
t
2 время
1
r2
Y
t t 2 t1 .

12.

r - вектор перемещения
r
s
s - пройденный путь

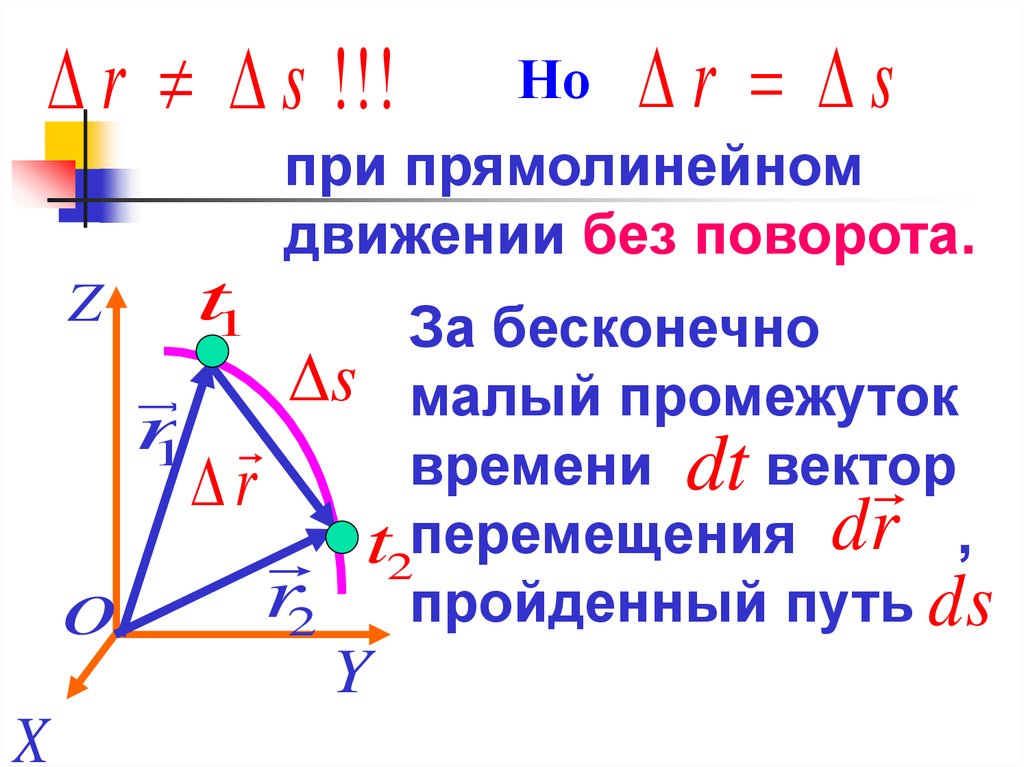
13.

r s !!!
Но
r s
при прямолинейном
движении без поворота.
Z
t1
За бесконечно
s малый промежуток
r1
времени dt вектор
r
d
r
перемещения
,
t
2
r2 пройденный путь ds
o
Y
X

14.

Скорость
r1 r
o
r2
r
t
характеризует быстроту
изменения положения
МТ в пространстве.
s Вектор средней
скорости
r
t
;
- модуль средней
скорости перемещения;
s
- средняя путевая скорость
t

15.

o
Вектор мгновенной
cкорости ( в данный
момент времени)
r dr
r
r1 r s lim
t 0 t
dt
r2
Модуль мгновенной
скорости
s ds
lim
t 0 t
dt

16.

r
Вектор скорости
направлен по
касательной к траектории, вектор
- по вектору перемещения r

17. Скорость и ее проекции связаны соотношением:

x i y j
(движение в плоскости ХОУ).
Проекция
на
х
i
x ось Х - производная
j
координаты x по
y
dx
времени t
x ;
y
dy
y
dt
dt
на ось У – произ-
- проекция
водная координаты у по t;
модуль вектора скорости
2
x
2
y

18.

Закон сложения скоростей
0
- cкорость тела в «неподвижной»
cистеме
отсчета
(абсолютная);
- cкорость тела в «движущейся»
cистеме отсчета (относитель ная);
0 - переносная скорость
подвижной системы отсчета.

19.

Ускорение
Характеризует быстроту
изменения скорости по
величине и направлению.
a
t
- вектор среднего
ускорения , направлен
по вектору изменения
скорости.

20.

Вектор ускорения в данный
момент времени – производ
ная вектора скорости по
времени :
d
a lim
.
t 0 t
dt
Проекции вектора ускорения
координатные оси Х и Y
aна
d y
d x
ax
x ; a y
y .
dt
dt

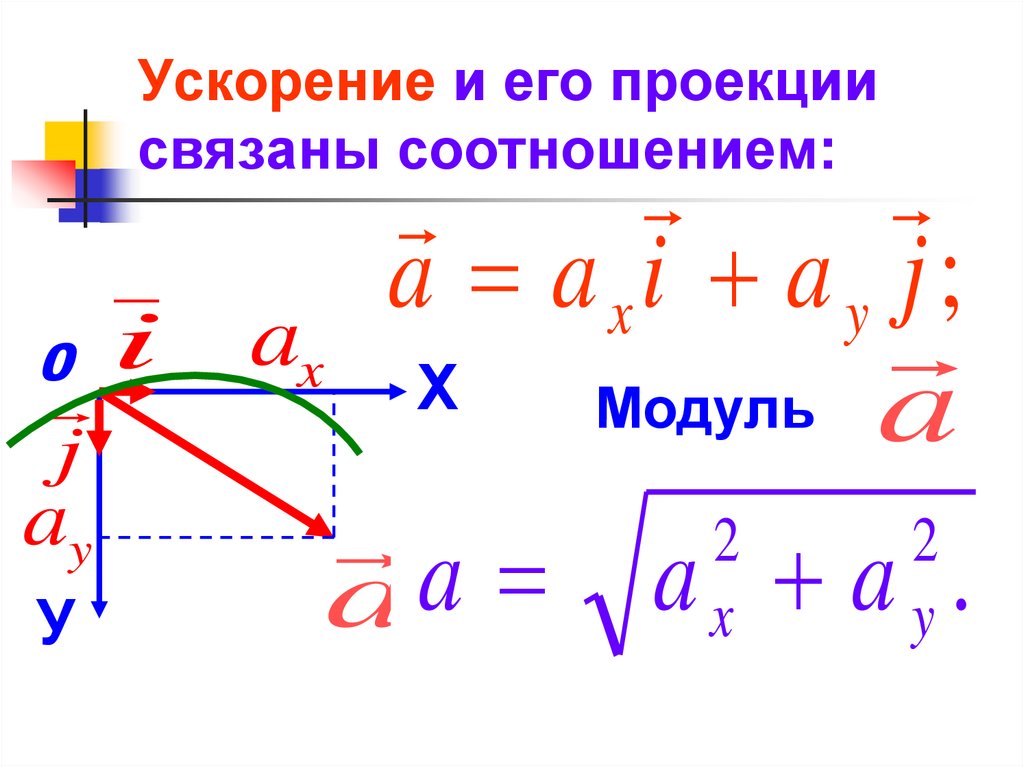
21. Ускорение и его проекции связаны соотношением:

0
j
ay
У
i
a axi a y j ;
ax
Х
Модуль a
a
a
a a .
2
x
2
y

22.

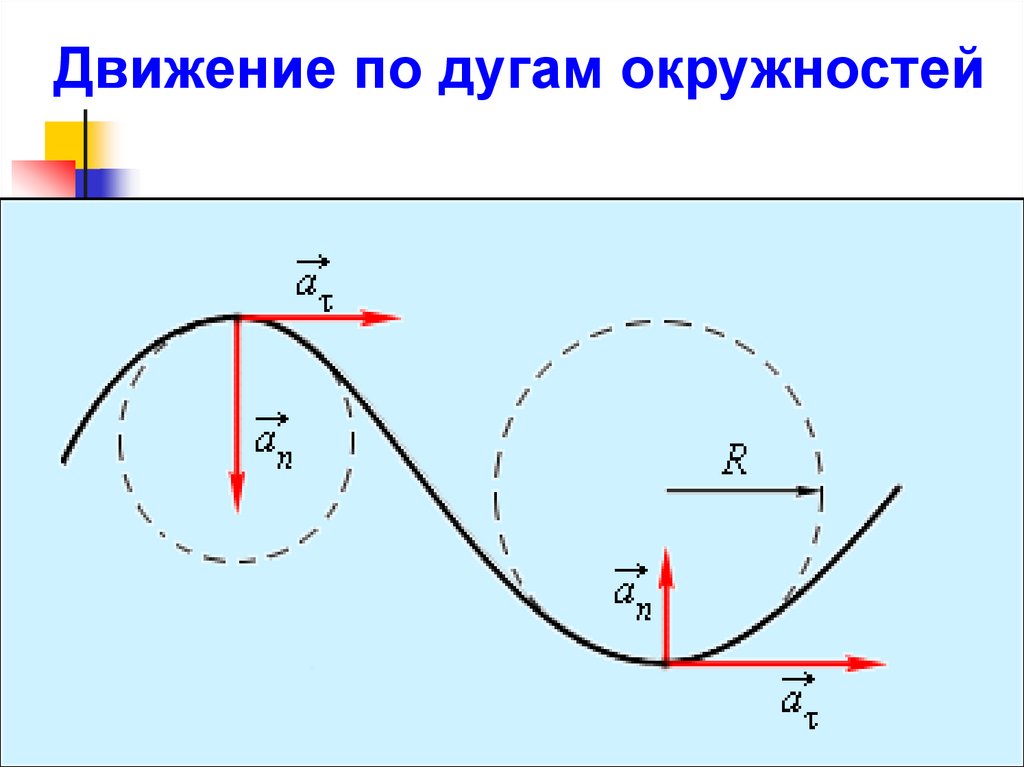
a на направления
Проекции
касательной к траектории и
нормали к касательной :
2
2
a a a n n , a a a n ,
n
a n
r
0
d
a
dt
- тангенциальное
a
a
ускорение -
an
r
2
- нормальное
ускорение -

23.

Движение по дугам окружностей

24. КИНЕМАТИЧЕСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ

Выражают зависимость от
времени радиус - вектора
МТ
или ее координат x , y , z
r
r r t , x x t , y y t , z z t .
3
2
r 3t i 5 t j tk .
Например,

25.

Скорость МТ
2
r 9t i 10 t j k ,
ее ускорение
a r 1 8 t i 1 0 j .
Для МТ, движущейся вдоль оси Х:
x 3 2t 5t t ;
2
3
x x 2 10t 3t ;
a x x x 10 6t .
2

26.

Движение тела, брошенного
под углом к горизонту