Построение сечений тетраэдра и параллелепипеда

1. Построение сечений тетраэдра и параллелепипеда

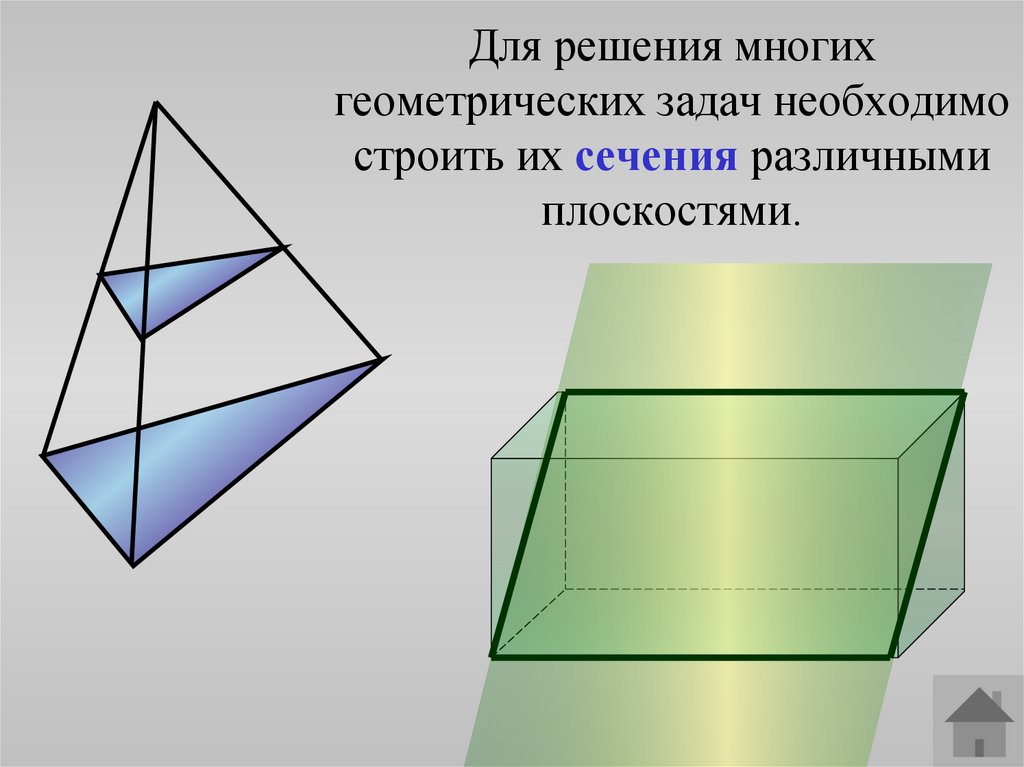
2. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.

3.

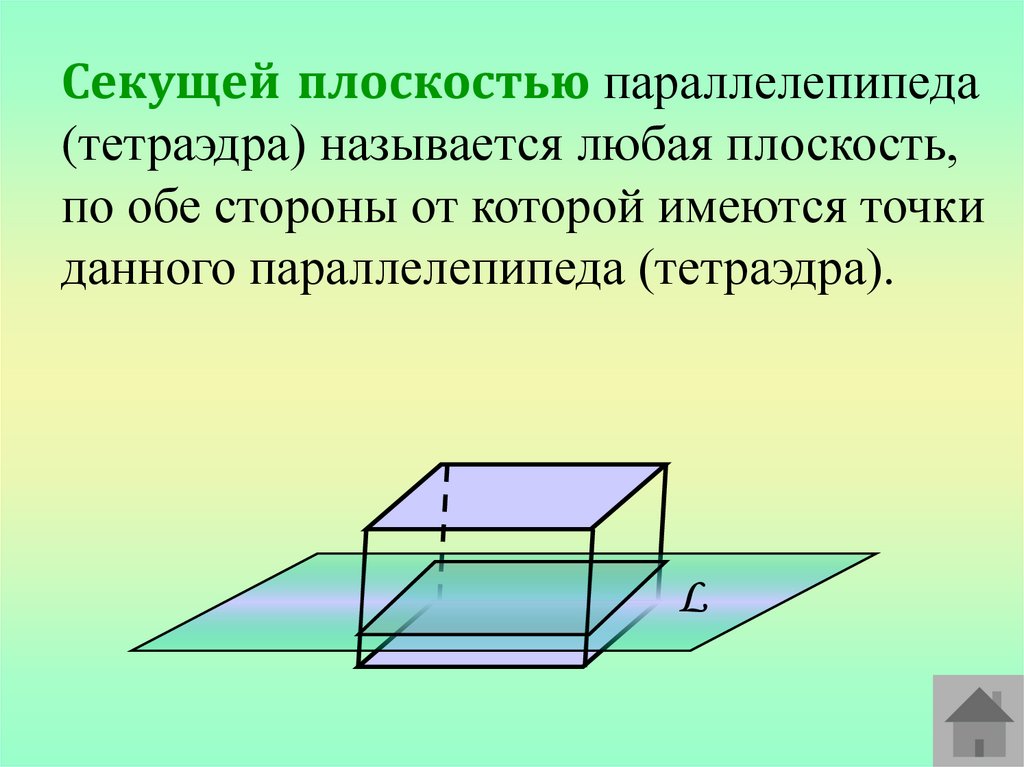
Секущей плоскостью параллелепипеда
(тетраэдра) называется любая плоскость,
по обе стороны от которой имеются точки
данного параллелепипеда (тетраэдра).
L

4.

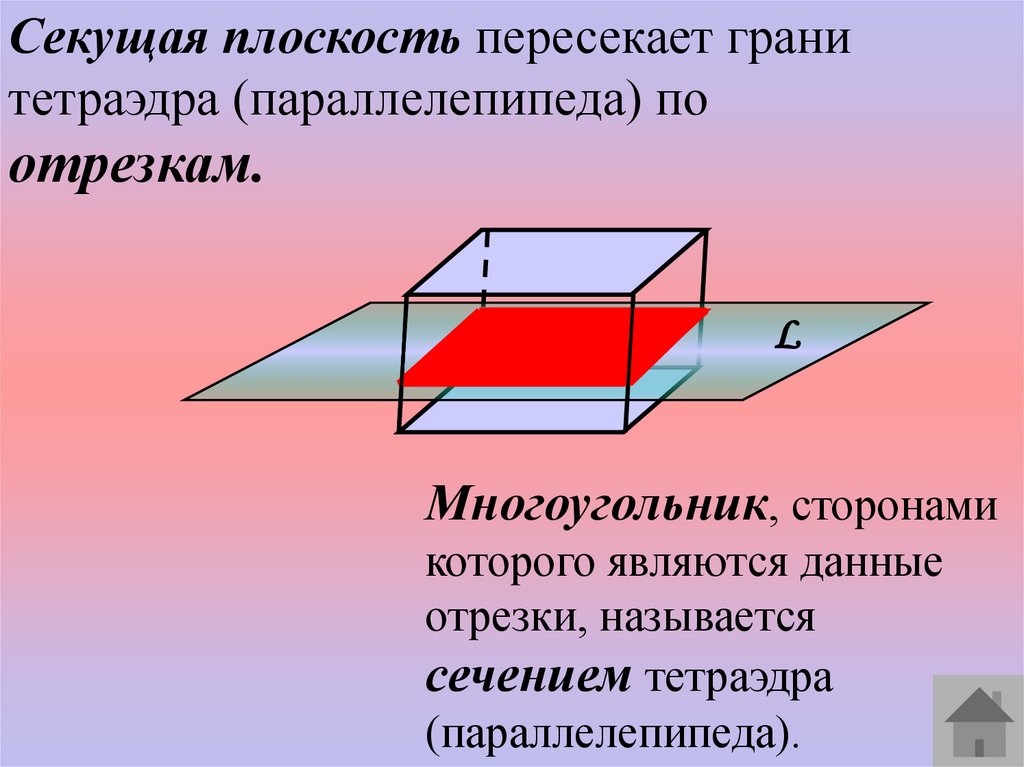
Секущая плоскость пересекает грани
тетраэдра (параллелепипеда) по
отрезкам.
L
Многоугольник, сторонами
которого являются данные
отрезки, называется
сечением тетраэдра
(параллелепипеда).

5. При этом необходимо учитывать следующее:

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
При этом необходимо учитывать следующее:
1. Соединять можно только две точки, лежащие
в плоскости одной грани.
2. Секущая плоскость пересекает
параллельные
грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна
точка, принадлежащая плоскости сечения, то надо
построить дополнительную точку. Для этого
необходимо найти точки пересечения уже
построенных прямых с другими прямыми,
лежащими в тех же гранях.

6.

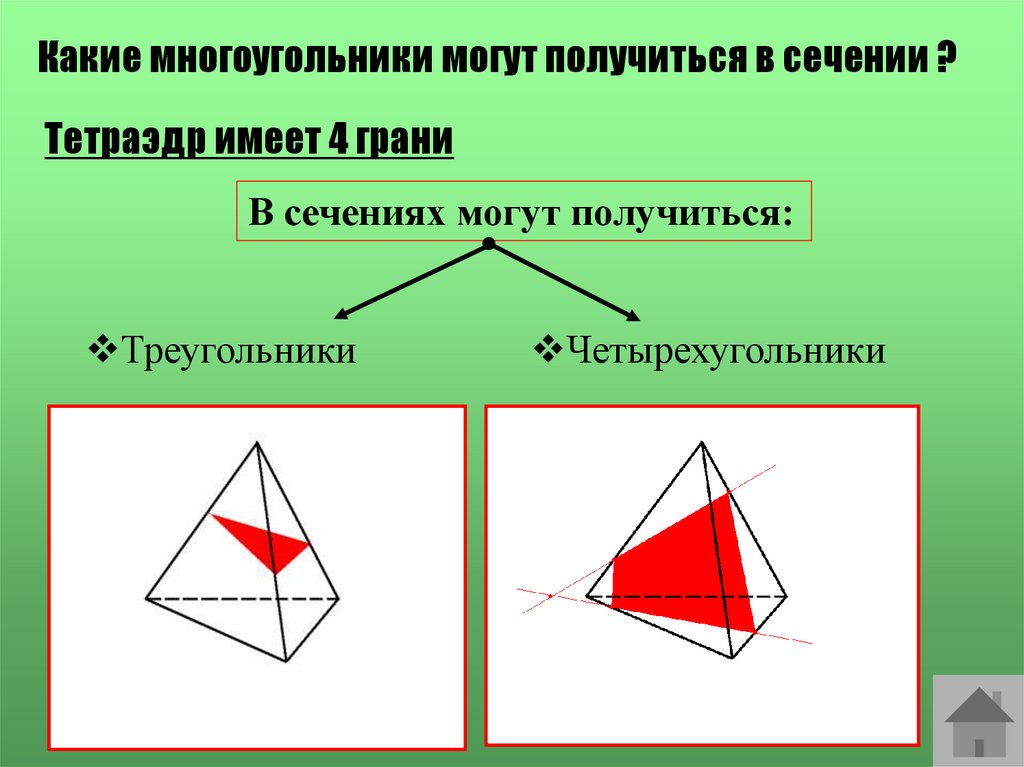
Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В сечениях могут получиться:
Треугольники
Четырехугольники

7.

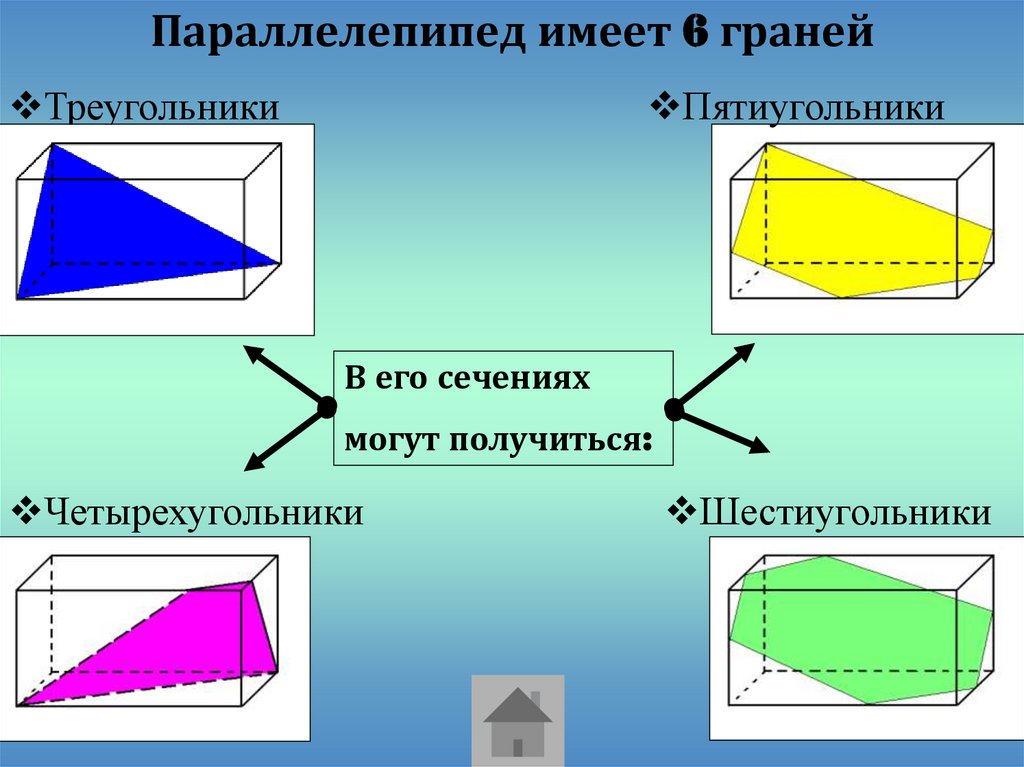
Параллелепипед имеет 6 граней
Треугольники
Пятиугольники
В его сечениях
могут получиться:
Четырехугольники
Шестиугольники

8.

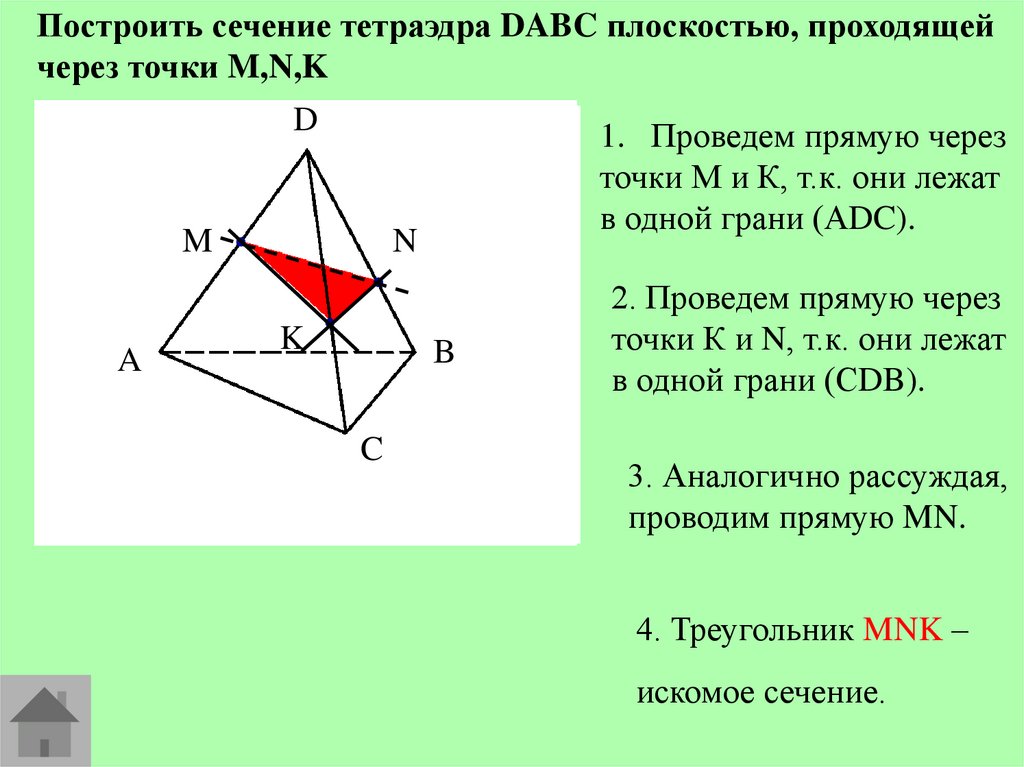
Построить сечение тетраэдра DABC плоскостью, проходящей
через точки M,N,K
D
M
AA
1. Проведем прямую через
точки М и К, т.к. они лежат
в одной грани (АDC).
N
K
BB
C
C
2. Проведем прямую через
точки К и N, т.к. они лежат
в одной грани (СDB).
3. Аналогично рассуждая,
проводим прямую MN.
4. Треугольник MNK –
искомое сечение.

9.

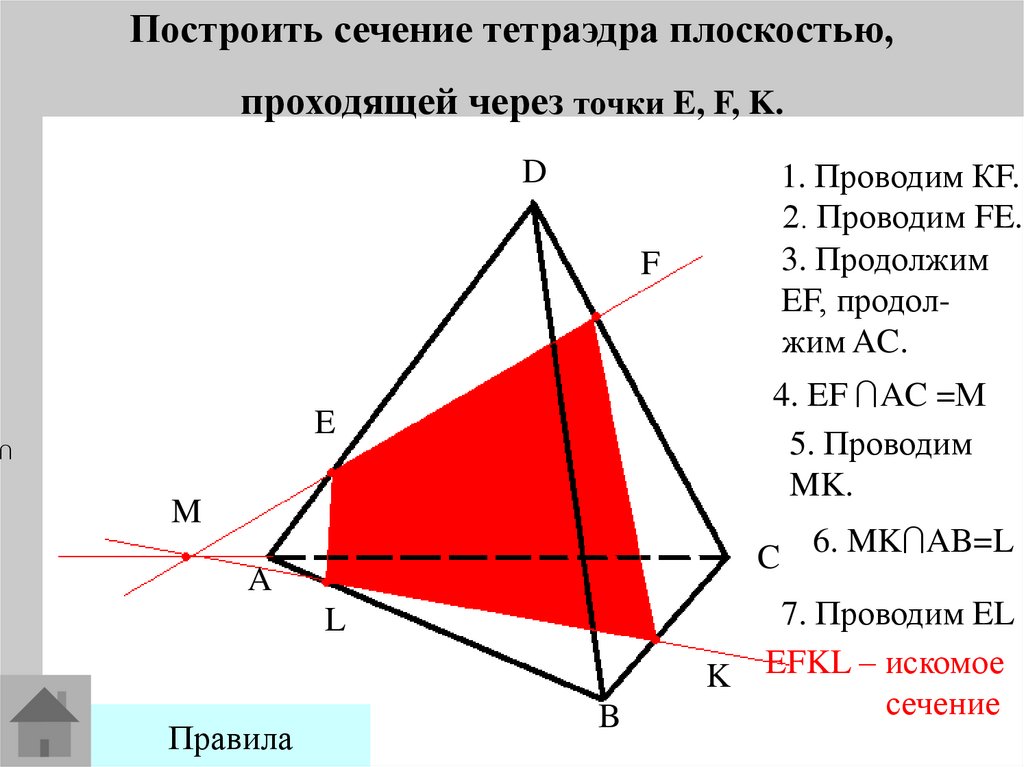
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
1. Проводим КF.
2. Проводим FE.
3. Продолжим
EF, продолжим AC.
D
F
4. EF AC =М
5. Проводим
MK.
E
M
C 6. MK AB=L
A
L
K
Правила
B
7. Проводим EL
EFKL – искомое
сечение

10.

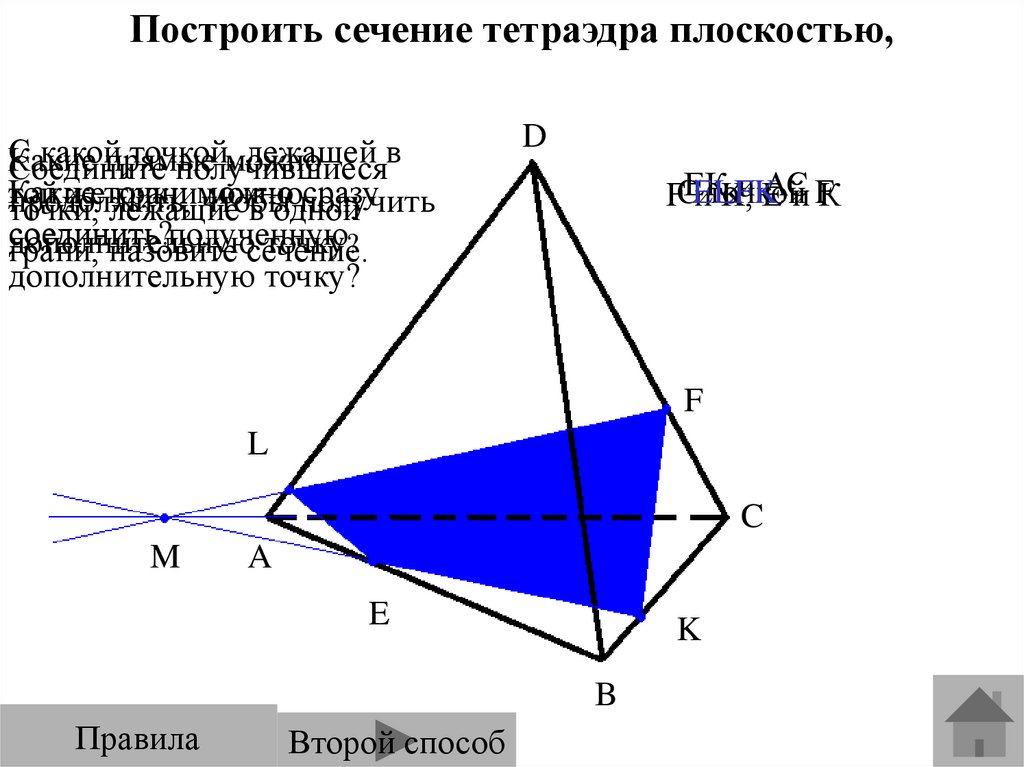
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
С
какойпрямые
точкой,
лежащей в
Какие
можно
Соедините
получившиеся
Какие
сразу
той
жеточки
граниможно
можно
продолжить,
чтобы
получить
точки,
лежащие
в одной
соединить?
соединить
полученную
дополнительную
точку?
грани, назовите
сечение.
дополнительную точку?
D
иЕ
АС
ЕLFK
FСЕК
иточкой
K,
и FК
F
L
C
M
A
E
K
B
Правила
Второй способ

11.

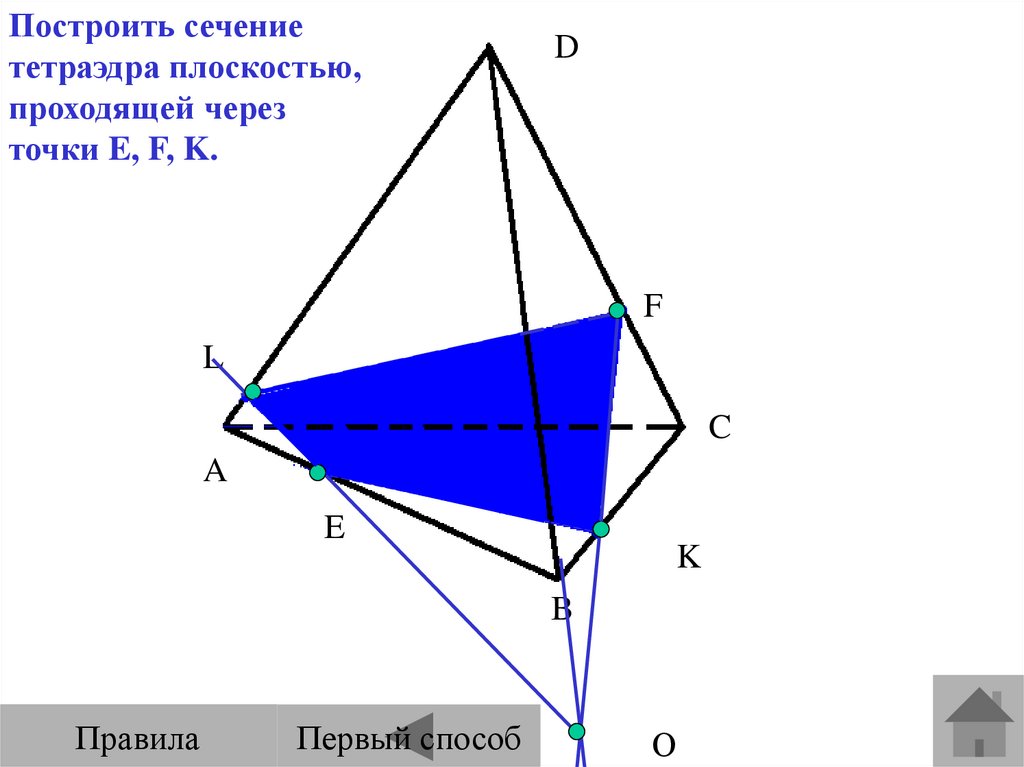
Построить сечение
тетраэдра плоскостью,
проходящей через
точки E, F, K.
D
F
L
C
A
E
K
B
Правила
Первый способ
О

12.

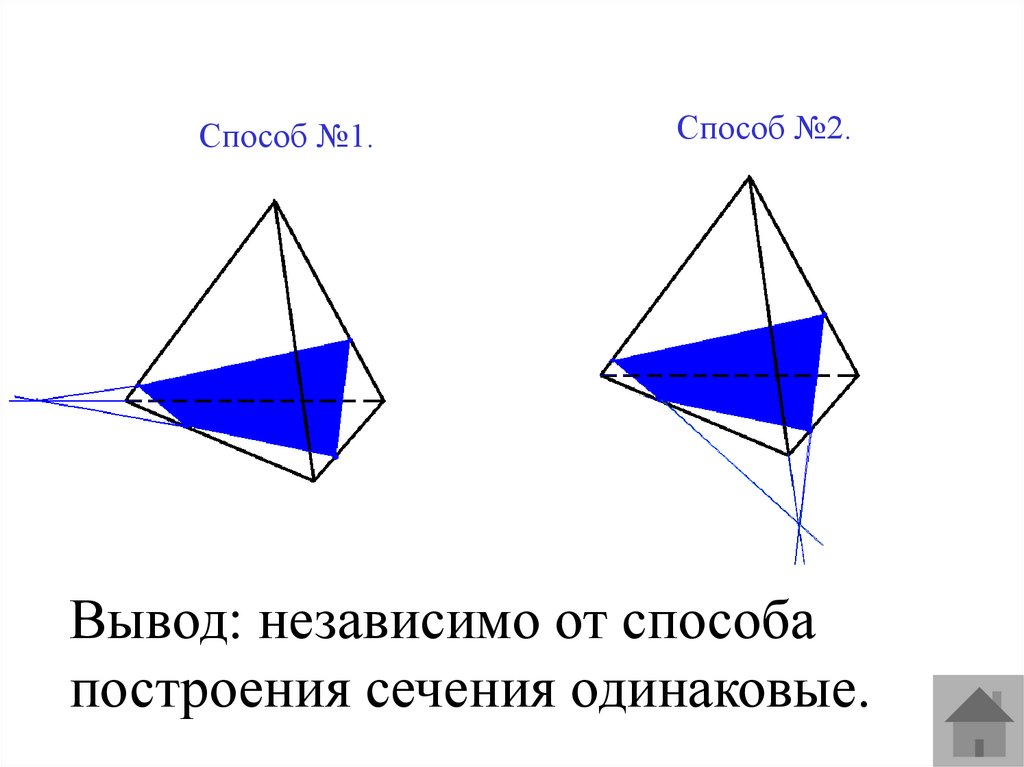
Способ №1.
Способ №2.
Вывод: независимо от способа
построения сечения одинаковые.

13.

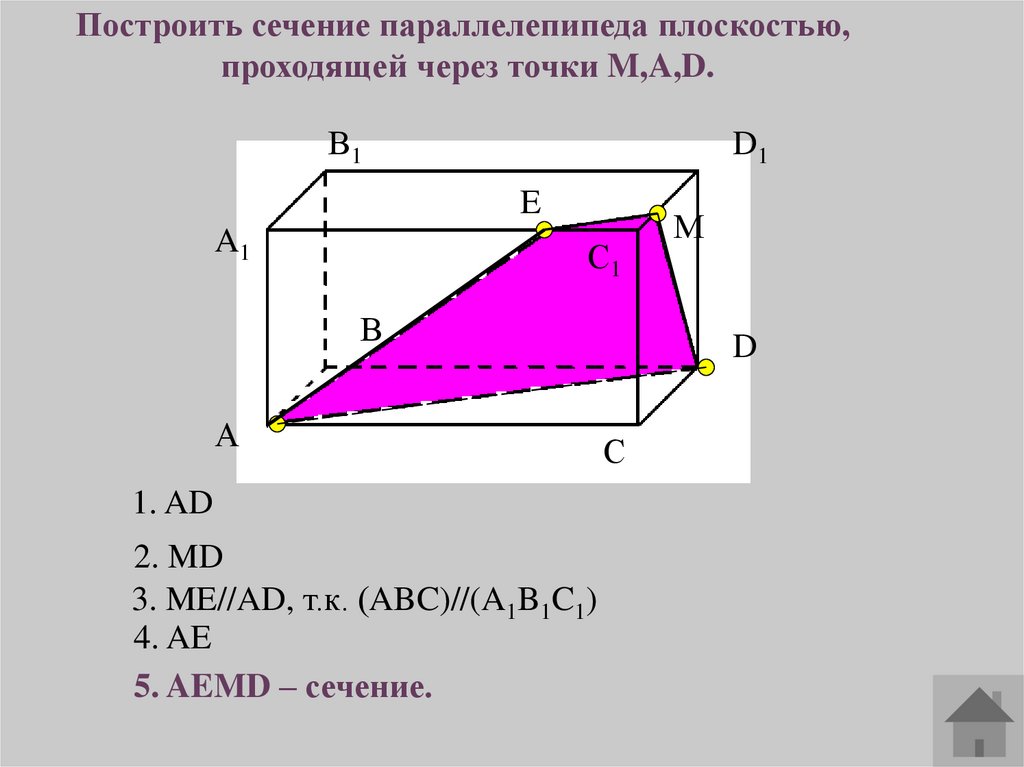
Построить сечение параллелепипеда плоскостью,
проходящей через точки M,A,D.
В1
D1
E
A1
С1
В
А
1. AD
2. MD
3. ME//AD, т.к. (ABC)//(A1B1C1)
4. AE
5. AEMD – сечение.
М
D
С

14.

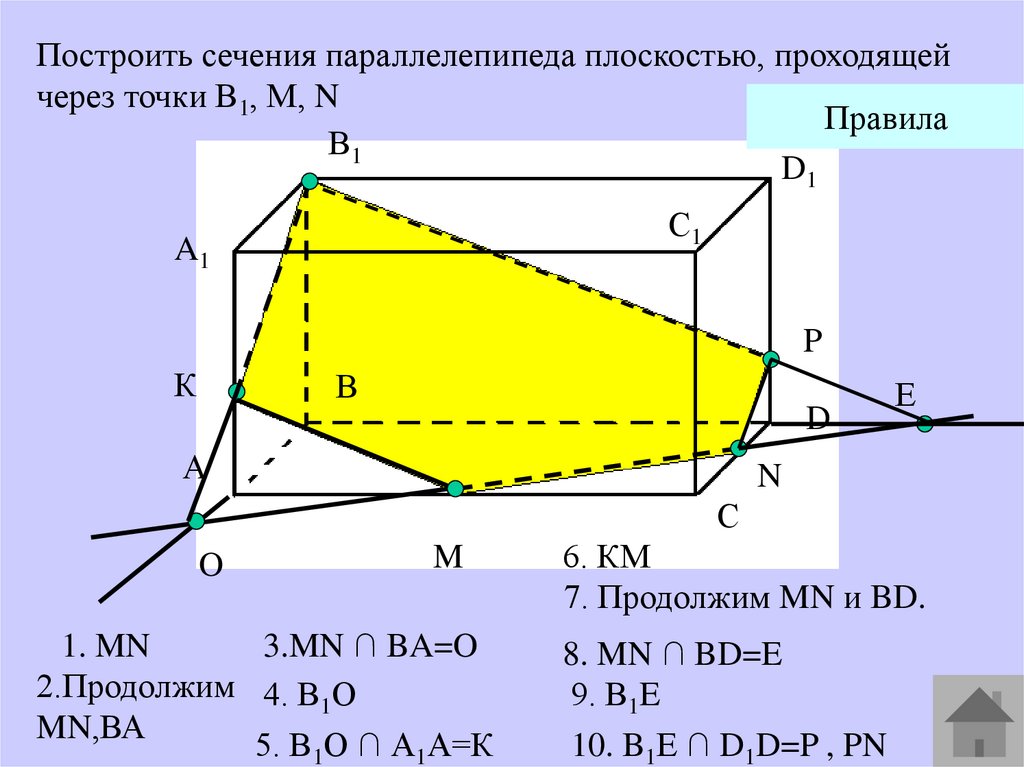
Построить сечения параллелепипеда плоскостью, проходящей
через точки В1, М, N
Правила
В1
D1
С1
A1
P
К
В
D
А
Е
N
С
O
M
1. MN
3.MN ∩ BA=O
2.Продолжим 4. В1О
MN,ВА
5. В1О ∩ А1А=К
6. КМ
7. Продолжим MN и BD.
8. MN ∩ BD=E
9. В1E
10. B1Е ∩ D1D=P , PN