Регресійний аналіз багатофакторних технічних систем

1. РЕГРЕСІЙНИЙ АНАЛІЗ БАГАТОФАКТОРНИХ ТЕХНІЧНИХ СИСТЕМ

1. Сутність регресійного аналізу та його задачі
2. Матричний метод знаходження коефіцієнтів
регресії
3. Приклади реалізації

2.

• Регресійний аналіз є одним з найбільш розроблених методів
дослідження виробничих процесів. Його використовують як
ефективний інструмент визначення функції відгуку,
Y f ( x1 , x2 , ... xi , ... xn )
яка встановлює на основі експериментальних даних аналітичний
зв’язок між випадковою величиною Y – параметром оптимізації і
незалежними змінними
X1, X2, …….., Xn
x1 , x2 , ... xi , ... xn
f ( x1, x2 , ... xi , ... xn )
– факторами.
Y
2

3. Природа зв’язку між факторами і параметром оптимізації носить випадковий (але статистично визначений!) характер і залежить від:

похибки вимірювань параметру
оптимізації за умови, що похибки
вимірювання факторів незначні настільки,
що їх можна не брати до уваги;
наявності неконтрольованих факторів, які
при кожному новому сполученні факторів
призводять до випадкових відхилень
параметру оптимізації.
3

4.

• Кількісною оцінкою випадкової величини
параметру оптимізації є його
математичне сподівання (середнє
очікуване значення). В регресійному
аналізі математичне сподівання
виражають поліномом виду:
M [Y ] o 1 x1 2 x2 ... i xi ... n xn
де β0, β1, β2 ... βn – коефіцієнти поліному.
4

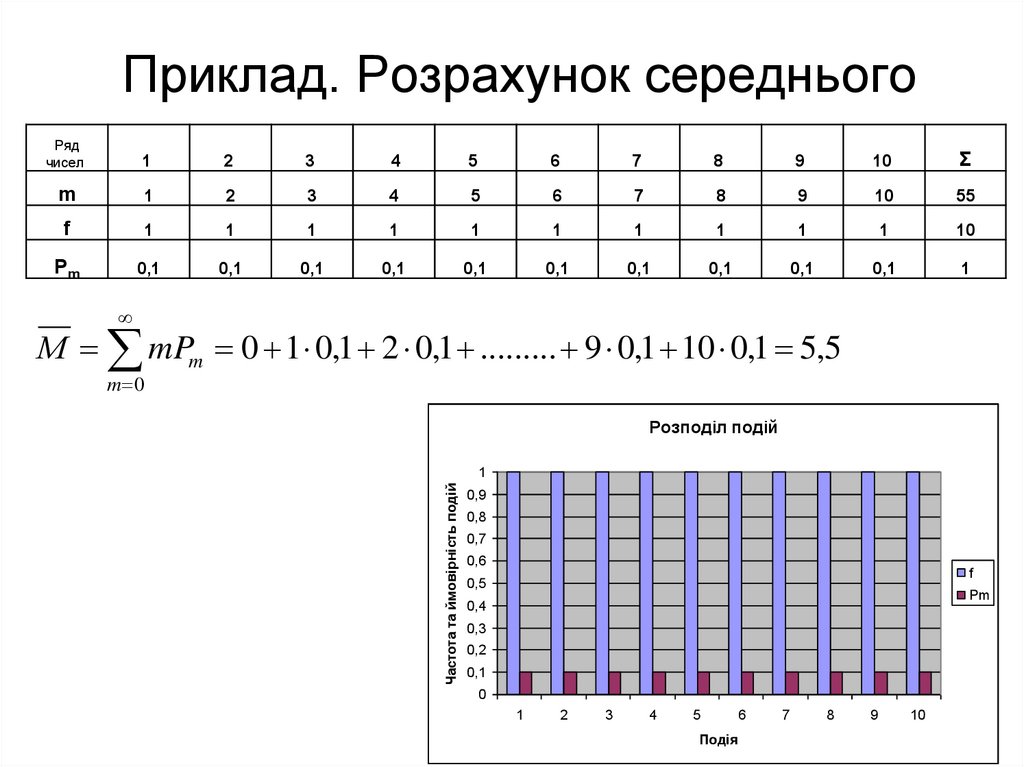
5. Приклад. Розрахунок середнього

Ряд
чисел
1
2
3
4
5
6
7
8
9
10
Ʃ
m
1
2
3
4
5
6
7
8
9
10
55
f
1
1
1
1
1
1
1
1
1
1
10
Pm
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
0,1
1
М mPm 0 1 0,1 2 0,1 ......... 9 0,1 10 0,1 5,5
m 0
Розподіл подій
Частота та ймовірність подій
1
0,9
0,8
0,7
0,6
f
0,5
Pm
0,4
0,3
0,2
0,1
0
1
2
3
4
5
6
Подія
7
8
9
10

6.

Ряд
чисел:
m
f
Pm
Ʃ
1
1
4
0
5
0
6
4
6
5
7
6
7
7
7
8
8
9
10
10
61
1
0
0
1
1
2
3
1
0
1
10
0,1
0
0
0,1
0,1
0,2
0,3
0,1
0
0,1
1
Розподіл подій
Ймовірність подій
0,3
0,2
Pm
0,1
0
1
2
3
4
5
6
7
8
9
10
Подія
М mPm 0 1 0,1 2 0 3 0 4 0,1 5 0,1 6 0,2 7 0,3 8 0,1 9 0 10 0,1 6,1
m 0

7.

• В практичній діяльності дослідник має
можливість провести деяку обмежену кількість
вимірювань, за результатами яких може бути
побудована математична модель процесу у
вигляді рівняння регресії:
Y b0 b1 x1 b2 x2 ... bi xi ... bn xn
де bi – статистичні оцінки коефіцієнтів βі
(і = 0, 1, 2, … i, … n). Прийнято вважати, що у
рівнянні регресії коефіцієнт b0 є множником
фіктивного фактора x 1 .
0
7

8. Для встановлення числових значень коефіцієнтів і в подальшій їх оцінці керуються наступними припущеннями:

1) випадкова величина Y (параметр оптимізації) має
нормальний розподіл похибки вимірювань, а
щільність цього розподілу визначається законом Гауса:
2
yi M y
1
f y
exp
2
2
2σ y
2π y
2
де
– дисперсія параметру оптимізації,
y
M ( y ) – математичне сподівання параметру оптимізації.
Математичне сподівання та дисперсію параметру
оптимізації вважають постійними величинами.
8

9.

2) точність встановлення факторів набагато вища точності
встановлення параметру оптимізації, тому фактори розглядають як
невипадкові величини, а параметр оптимізації – випадкову
величину.
3) у межах похибки визначення параметру оптимізації заданому
сполученню факторів
x1 , x2 , ... xi , ... xn
повинно відповідати цілком певне значення параметру Y, який
повинен мати фізичний зміст, область визначення і який розглядають як
один з найбільш інформативних параметрів системи, що досліджують.
4) незалежні змінні x , x , ... x , ... x повинні бути сумісними,
1
2
i
n
мати фізичний зміст та однозначний функціональний зв’язок з
параметром оптимізації Y.
9

10.

Задачами регресійного аналізу є:
• знаходження статистичних оцінок рівняння регресії;
• перевірка статистичних гіпотез про
контрольованість експерименту, значущість
коефіцієнтів регресії, адекватність отриманого
рівняння моделі.
Метою регресійного аналізу є моделювання станів
ТС із заданою точністю набором поліноміальних
n
функцій
Ymod X bi f i xi
i 1
де Х – вектор значень факторів;
Ymod X - відгук технічної системи,
bi – коефіцієнти поліному.
10

11.

• Множина можливих сполучень факторів і їхніх значень визначає
множину станів технічної системи. Теоретично ця множина може
бути необмеженою, однак практично її вважають скінченною.
• Якщо у виробничому експерименті модель враховує всі можливі
взаємодії факторів, то такий експеримент називається повним
факторним експериментом.
Y = b0 + b1x1 + b2x2 +...+ bnxn + b12x1x2 + b13 x1x3 +…bn-1,n xn-1xn+ …
+ bn+kx12 + bn+k+1x22 + … + bmxn2 + … =
= b0 + b1x1 + b2x2 + ... + bnxn + ... + bmxm + ...
11

12. Визначення коефіцієнтів регресії

• Коефіцієнти регресії bi визначають, виходячи з
критерію мінімізації суми квадратів різниці між
експериментально встановленими значеннями
параметра yj і модельним значенням параметра
yjmod у всіх експериментальних точках j = 1, 2, 3 ...
N, де N – кількість дослідів:
N
{ y j y j mod }min
j 1
2
• Рівність нулю частинних похідних визначає
систему n рівнянь з n невідомими, якими є
коефіцієнти bi рівняння регресії
N
2
y j y j mod 0
bi j 1
12

13. Ymod = b0 + b1x1 + b2x2 +...+ bnxn + b12x1x2 + b13 x1x3 +…bn-1,n xn-1xn+ … + bn+kx12 + bn+k+1x22 + … + bmxn2 + … = b0 + b1x1 +

b2x2 + ...
+ bnxn + ... + bmxm + ...
N
2
y j y j mod 0
bi j 1
N
N
N
N
N
j 1
j 1
j 1
j 1
j 1
b0 N b1 x1j b2 x2j ... bn xnj ... bm xmj y j
N
N
N
N
N
j 1
j 1
i 1
b0 x1j b1 x b2 x1j x2j ... bn x1j xnj ... x1j y j
j 1
j 1
N
N
2
1j
N
N
N
j 1
j 1
b0 x2j b1 x2j x1j b2 x 2 j ... bn x2j xni ... x2j y j
2
j 1
j 1
j 1
......................... .............
N
N
N
N
N
b0 xnj b1 xnj x1j b2 xnj x2j ... bn x nj ... xnj y j
2
j 1
j 1
j 1
j 1
i 1
13

14. Ліву частину системи рівнянь (*) можна представити добутком трьох матриць (XTX)B, а праву добутком двох матриць XTY, де Х –

матриця умов,
XT – транспонована матриця Х, В – матриця коефіцієнтів, Y – матриця
результатів (матриця станів), xkl – значення k-го фактора в l-му досліді.
1 x11
1 x12
X 1 x13
1 .
1 x
1N
x21
.
xn1
x11 x21
x22
x23
.
.
xn 2
xn3
x12 x22
x13 x23
.
xkl .
.
. xnN x1N x2 N
x2 N
x11 x31 . xn 1,1 xn,1
x12 x32 . xn 1,2 xn 2
x13 x33 . xn 1,3 xn3
.
. xn 1,l xnl
x1N x3 N . xn 1, N xnN
(XTX)B = XTY
1
В (Х Х ) (Х Y )
Т
Т
y1
y2
..
Y
yl
..
b0
y
N
b1
.
B
bn
.
b
m
14