Углы между прямыми и плоскостями (координатный метод) (11 класс)

1. Решение задач по теме «Углы между прямыми и плоскостями (координатный метод)».

Геометрия, 11 класс

2.

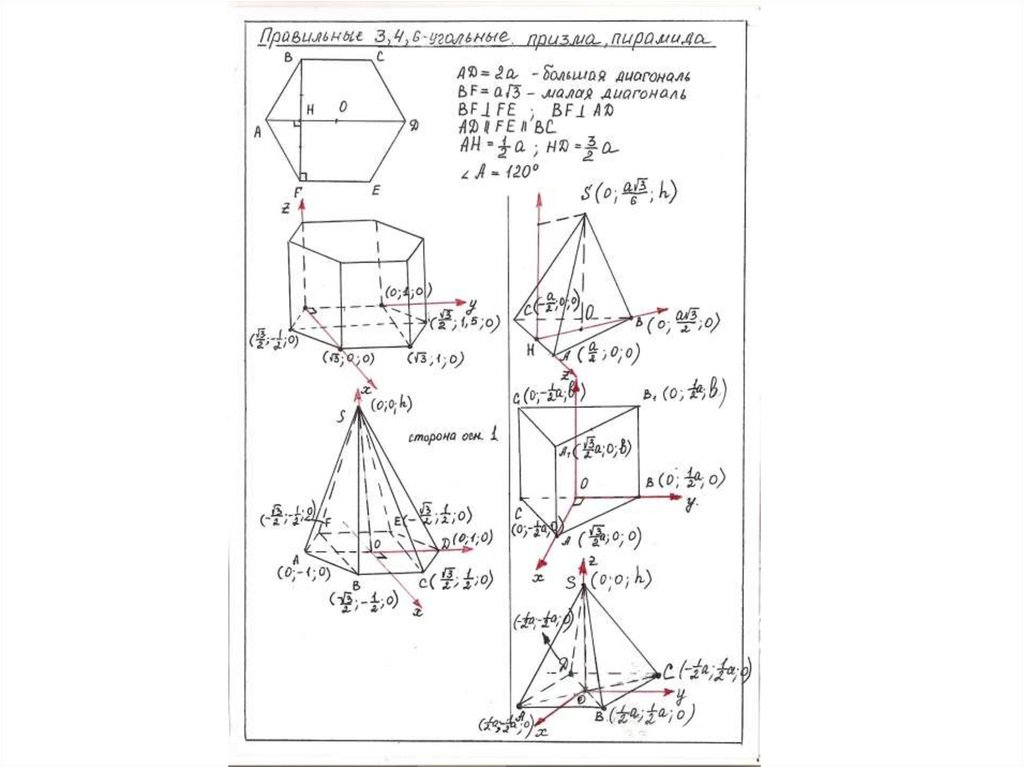
Скалярное произведение векторов.
a
b
a
b
cos
а
b
а x1;y1;z1 b x2;y2;z2
a
b
x
x
y
y
z
z
1
2
1
2
1
2
x
x
y
y
z
z
1
2
1
2
1
2
cos
2 2 2
2 2 2
x
y
z
x
y
z
1
1
1
2
2
2

3.

4.

1. Составить уравнение прямой :
а) проходящей через точку М(2; -3; 1) параллельно вектору р 3; 1;4 .
б) проходящей через точки А(4; -1;3) и В(0; 5; -1).

5.

6.

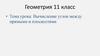
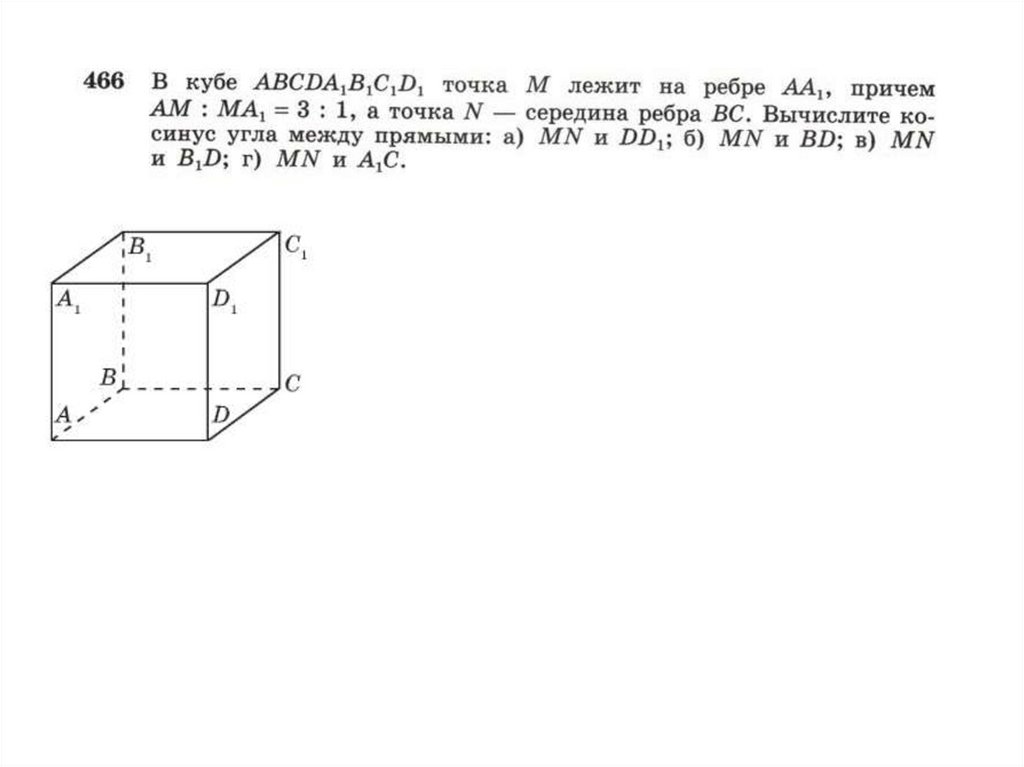
Ребро куба А…D1 равно 2. Найдите угол между прямыми А1М и В1N, где М –
середина CD, N – середина AD.

7.

8.

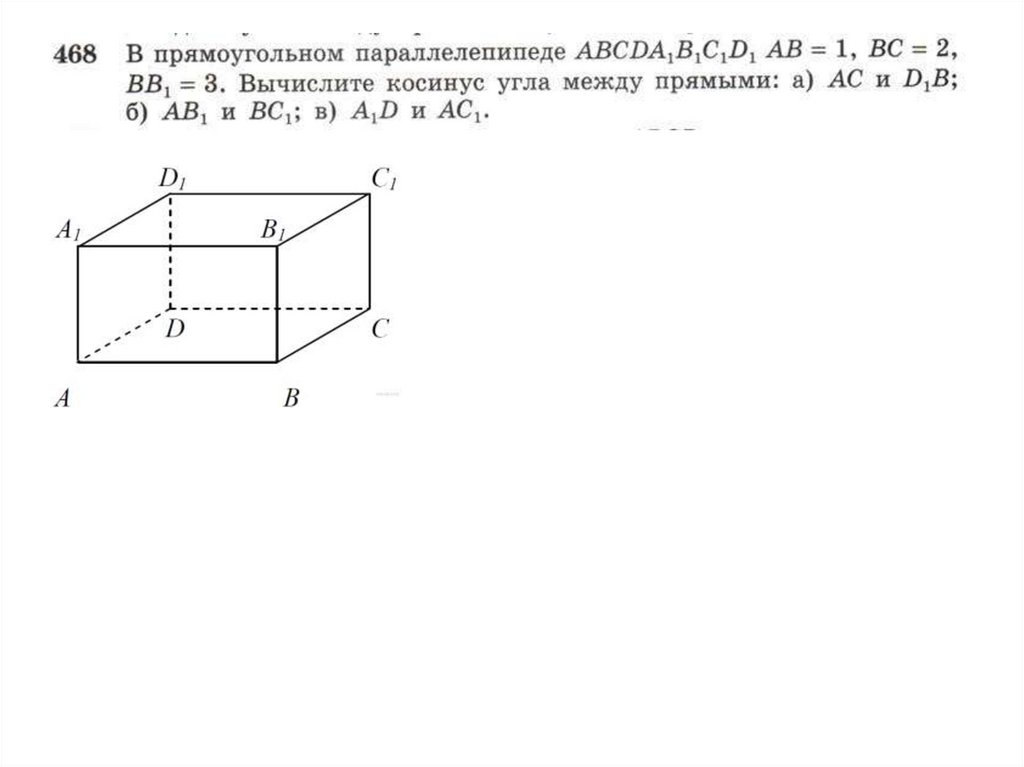
В правильной шестиугольной призме А…F1 найдите угол между прямыми
FB1 и АС1.

9.

10.

11.

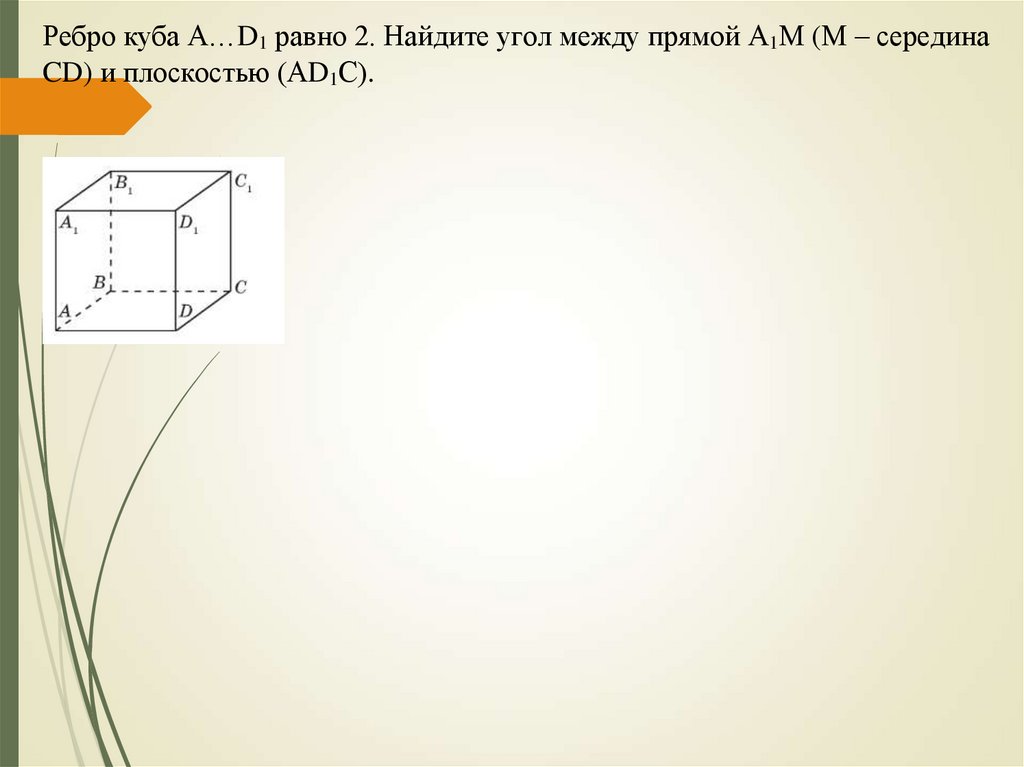
Ребро куба А…D1 равно 2. Найдите угол между прямой А1М (М – середина
CD) и плоскостью (АD1С).

12.

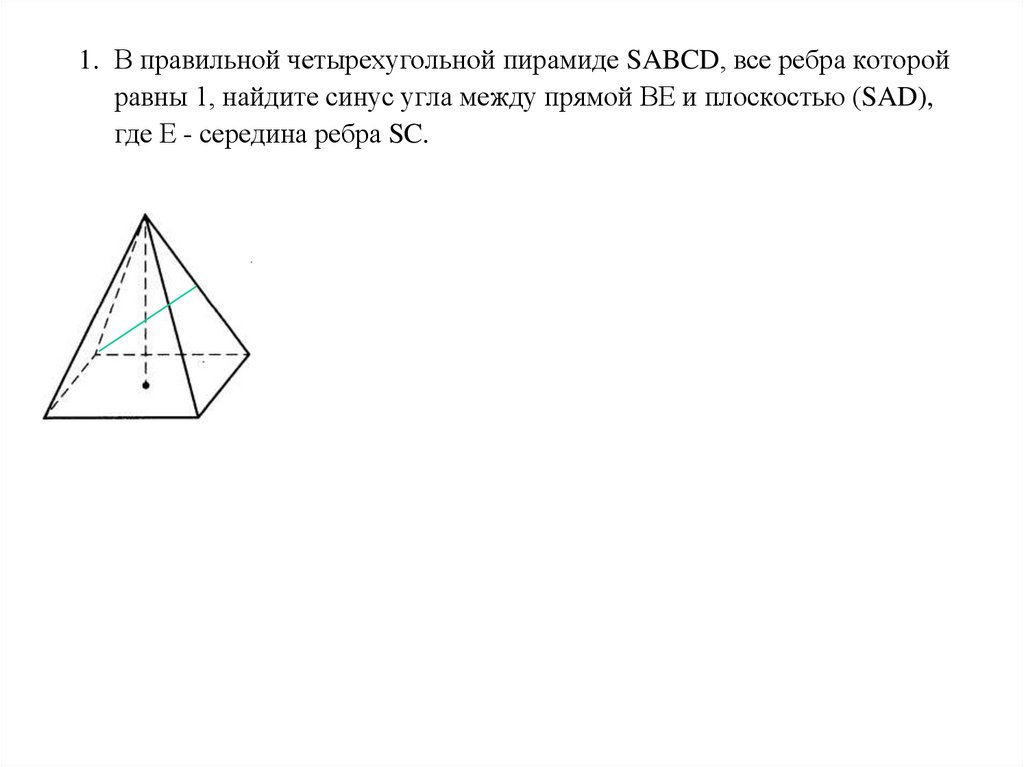
1. В правильной четырехугольной пирамиде SABCD, все ребра которой
равны 1, найдите синус угла между прямой ВЕ и плоскостью (SAD),
где Е - середина ребра SC.

13.

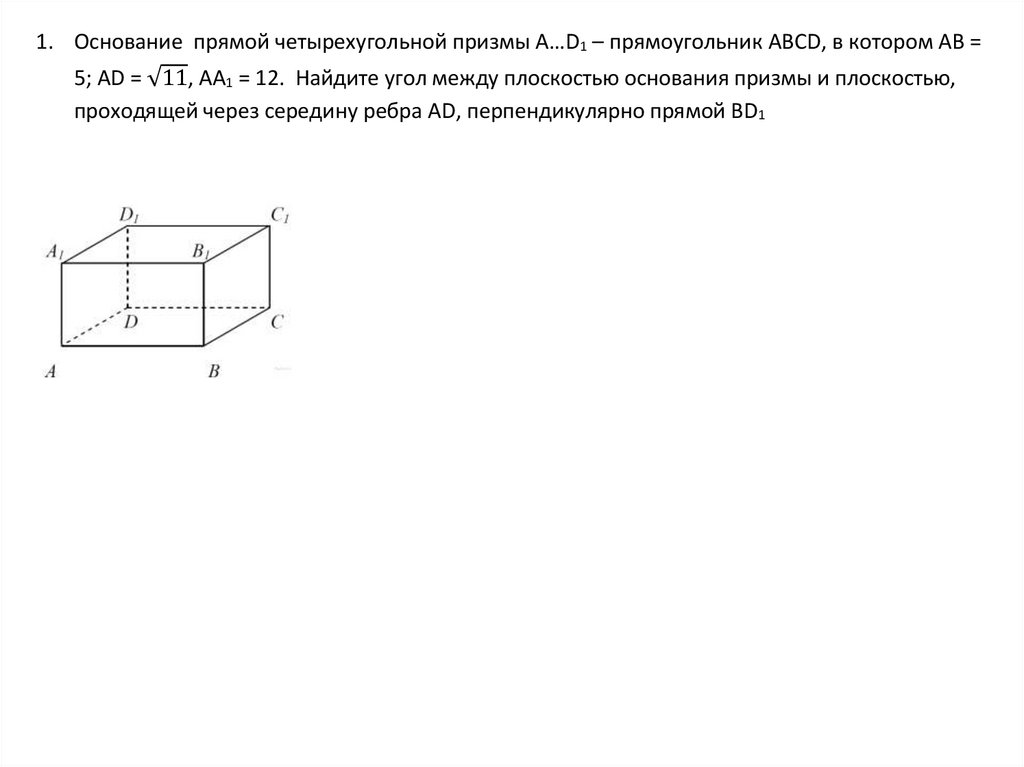
1. Основание прямой четырехугольной призмы А…D1 – прямоугольник АВСD, в котором АВ =
5; AD = 11, АА1 = 12. Найдите угол между плоскостью основания призмы и плоскостью,
проходящей через середину ребра АD, перпендикулярно прямой ВD1

14.

15.

16.

17.

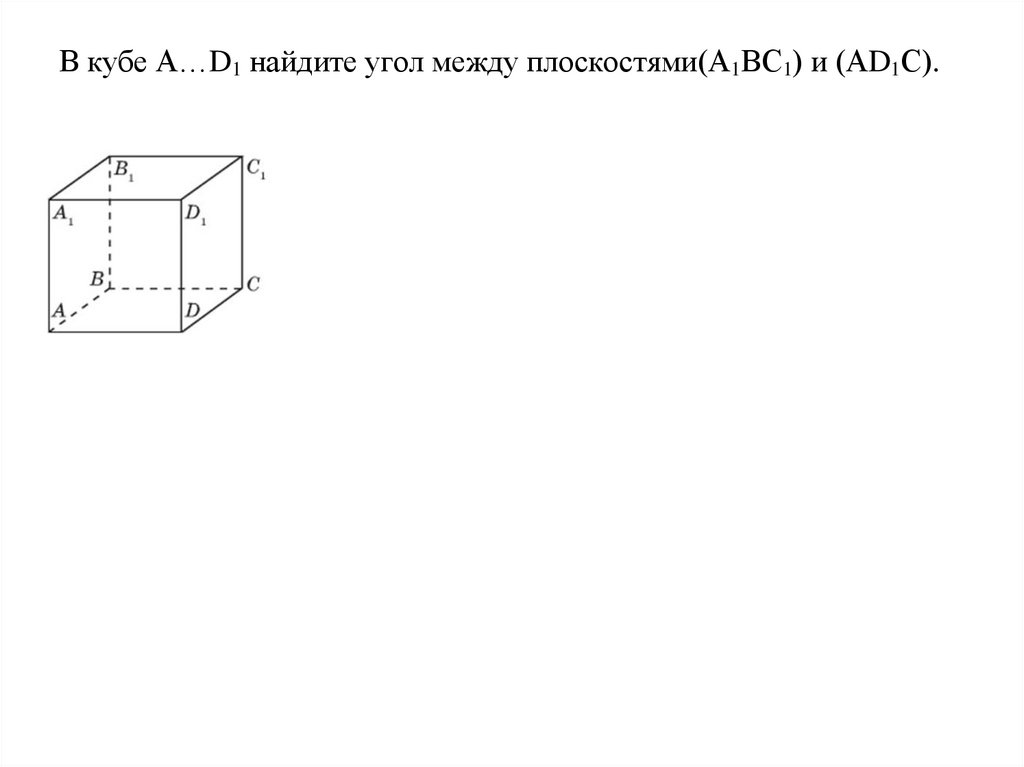
В кубе А…D1 найдите угол между плоскостями(А1ВС1) и (АD1С).

18.

Все рёбра правильной треугольной призмы ABCA1B1C1 имеют длину 6. Точки M и N—
середины рёбер AA1 и A1C1 соответственно.
а) Докажите, что прямые BM и MN перпендикулярны.
б) Найдите угол между плоскостями BMN и ABB1.

19.

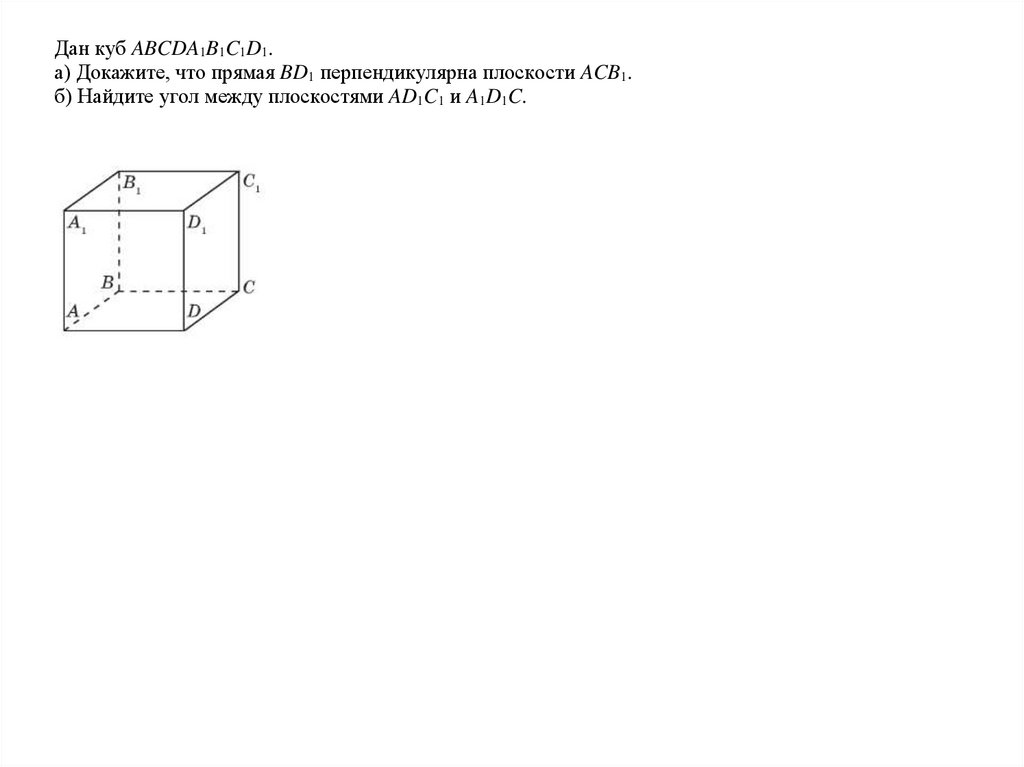
Дан куб ABCDA1B1C1D1.
а) Докажите, что прямая BD1 перпендикулярна плоскости ACB1.
б) Найдите угол между плоскостями AD1C1 и A1D1C.

20.

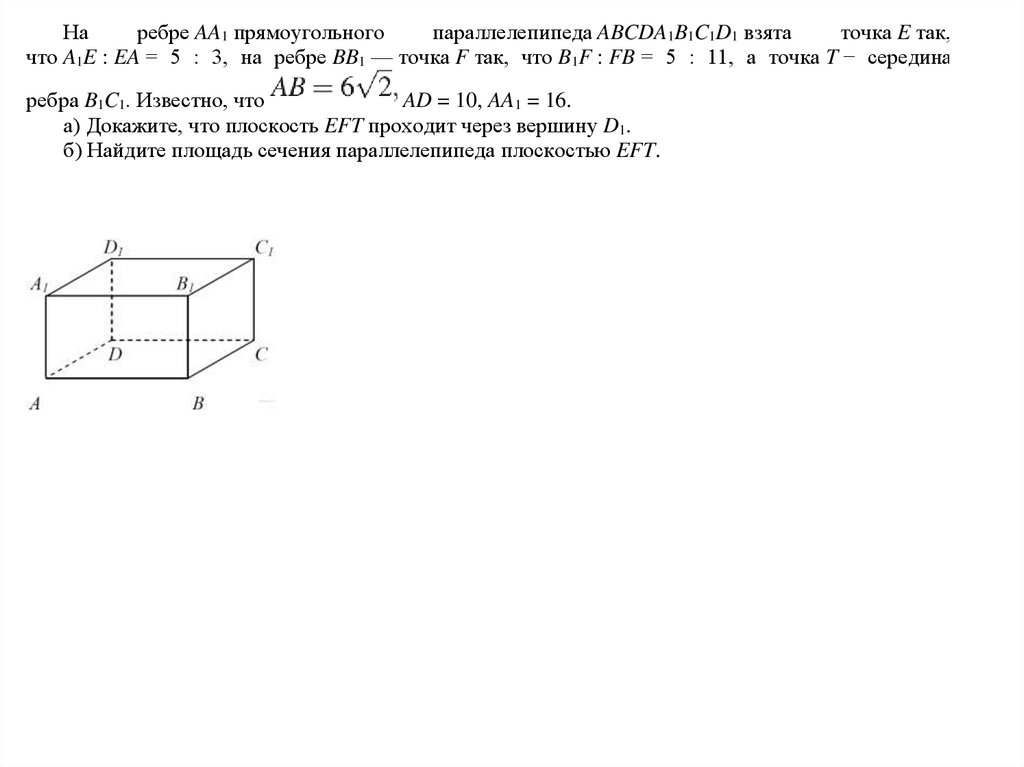
На
ребре AA1 прямоугольного
параллелепипеда ABCDA1B1C1D1 взята
точка E так,
что A1E : EA = 5 : 3, на ребре BB1 — точка F так, что B1F : FB = 5 : 11, а точка T − середина
ребра B1C1. Известно, что
AD = 10, AA1 = 16.
а) Докажите, что плоскость EFT проходит через вершину D1.
б) Найдите площадь сечения параллелепипеда плоскостью EFT.

21.

Длина ребра правильного тетраэдра ABCD равна 1. M — середина ребра BC, L — середина
ребра AB.
а) Докажите, что плоскость, параллельная прямой CL и содержащая прямую DM, делит
ребро AB в отношении 3 : 1, считая от вершины A.
б) Найдите угол между прямыми DM и CL.

22.

23.

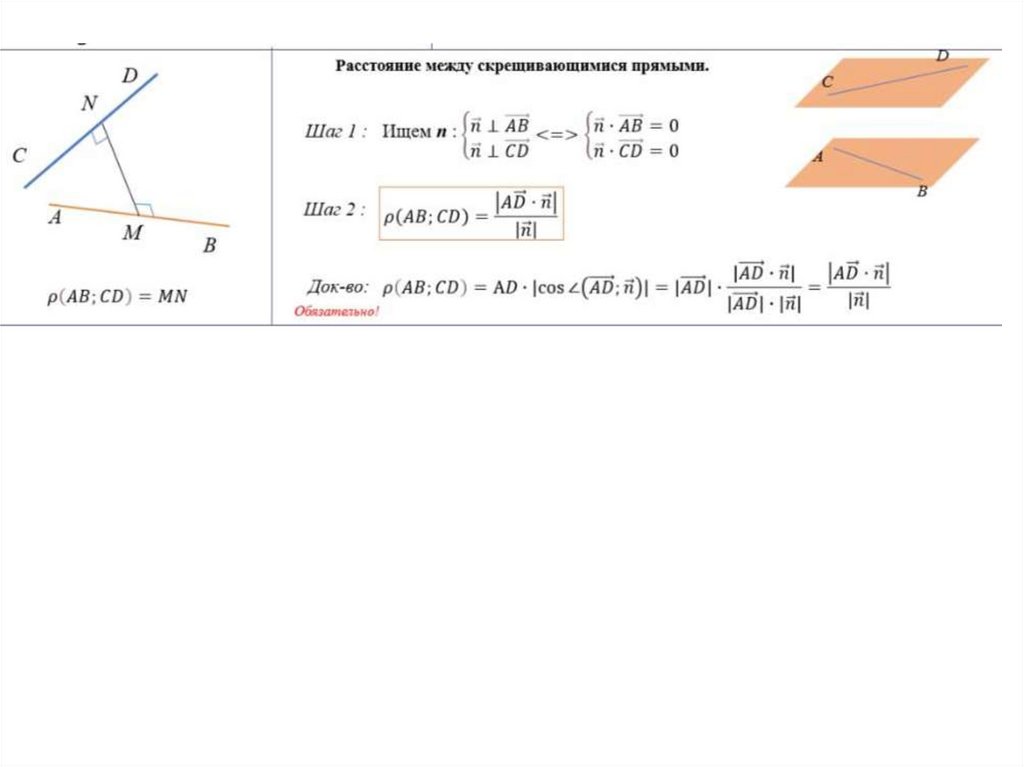
Вычислить расстояние между скрещивающимися диагоналями двух
соседних граней куба с ребром а.

24.

25.

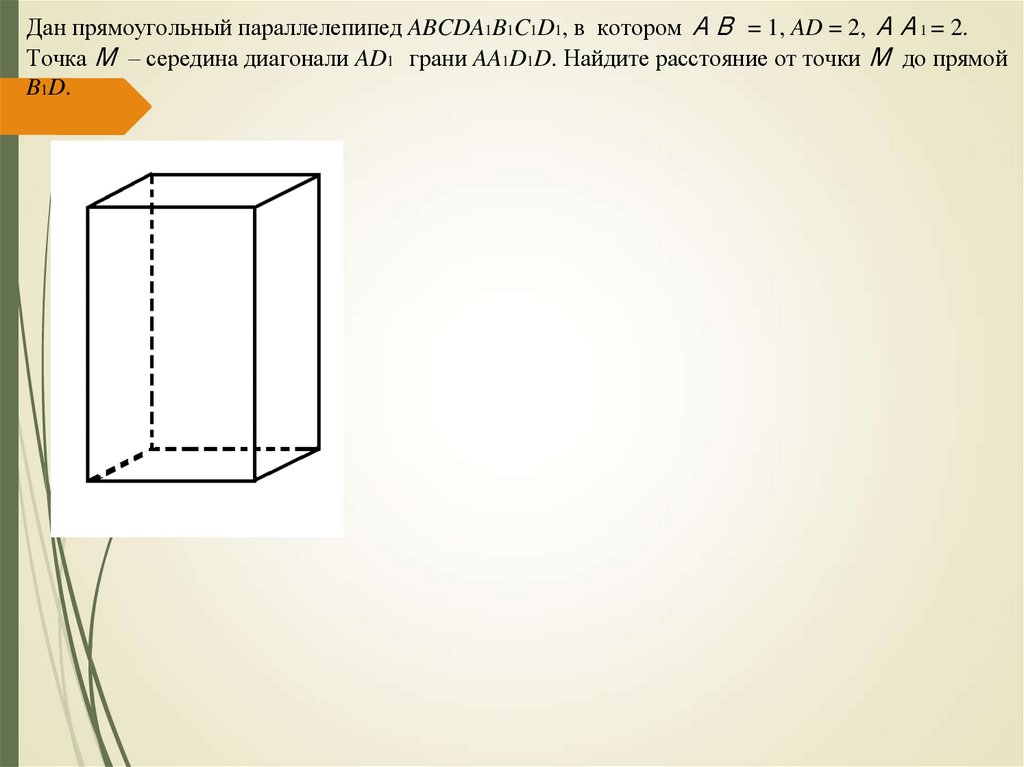
Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором АВ = 1, AD = 2, АА1 = 2.
Точка М – середина диагонали AD1 грани AA1D1D. Найдите расстояние от точки М до прямой
B1D.