Метод координат в пространстве

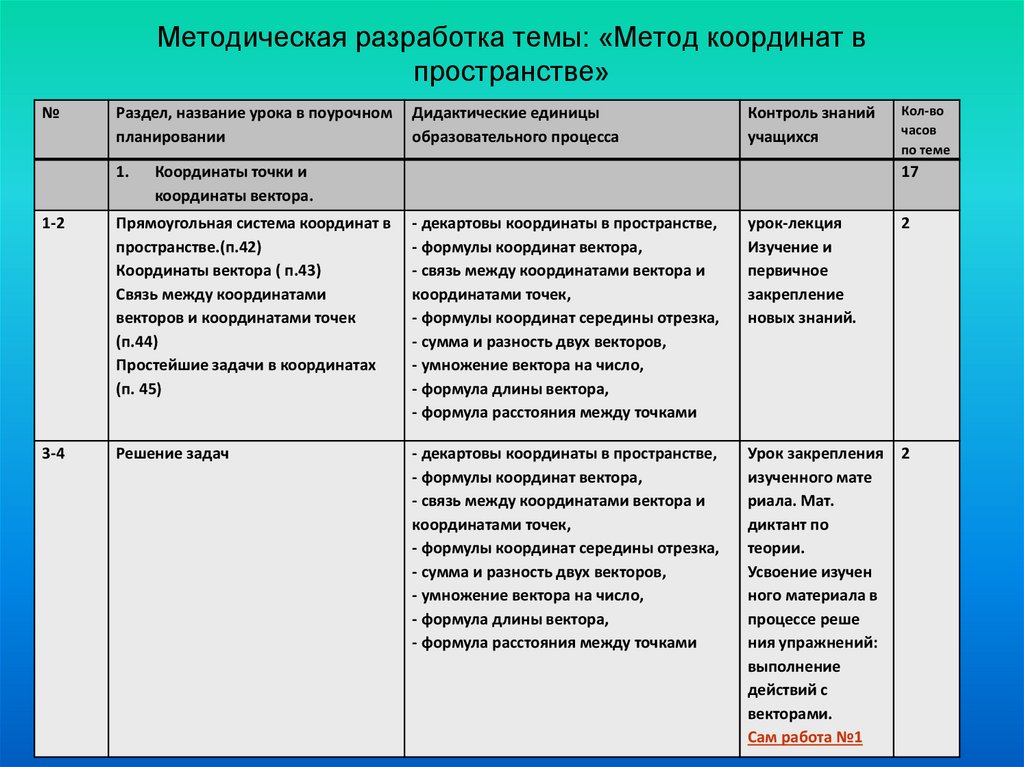
1. Методическая разработка темы: «Метод координат в пространстве»

№
Раздел, название урока в поурочном
планировании
1.
Дидактические единицы
образовательного процесса
Контроль знаний
учащихся
Координаты точки и
координаты вектора.
Кол-во
часов
по теме
17
1-2
Прямоугольная система координат в
пространстве.(п.42)
Координаты вектора ( п.43)
Связь между координатами
векторов и координатами точек
(п.44)
Простейшие задачи в координатах
(п. 45)
- декартовы координаты в пространстве,
- формулы координат вектора,
- связь между координатами вектора и
координатами точек,
- формулы координат середины отрезка,
- сумма и разность двух векторов,
- умножение вектора на число,
- формула длины вектора,
- формула расстояния между точками
урок-лекция
Изучение и
первичное
закрепление
новых знаний.
2
3-4
Решение задач
- декартовы координаты в пространстве,
- формулы координат вектора,
- связь между координатами вектора и
координатами точек,
- формулы координат середины отрезка,
- сумма и разность двух векторов,
- умножение вектора на число,
- формула длины вектора,
- формула расстояния между точками
Урок закрепления
изученного мате
риала. Мат.
диктант по
теории.
Усвоение изучен
ного материала в
процессе реше
ния упражнений:
выполнение
действий с
векторами.
Сам работа №1
2

2.

№
Раздел, название урока в поурочном
планировании
Дидактические единицы
образовательного процесса
Контроль знаний
учащихся
Кол-во
часов по
теме
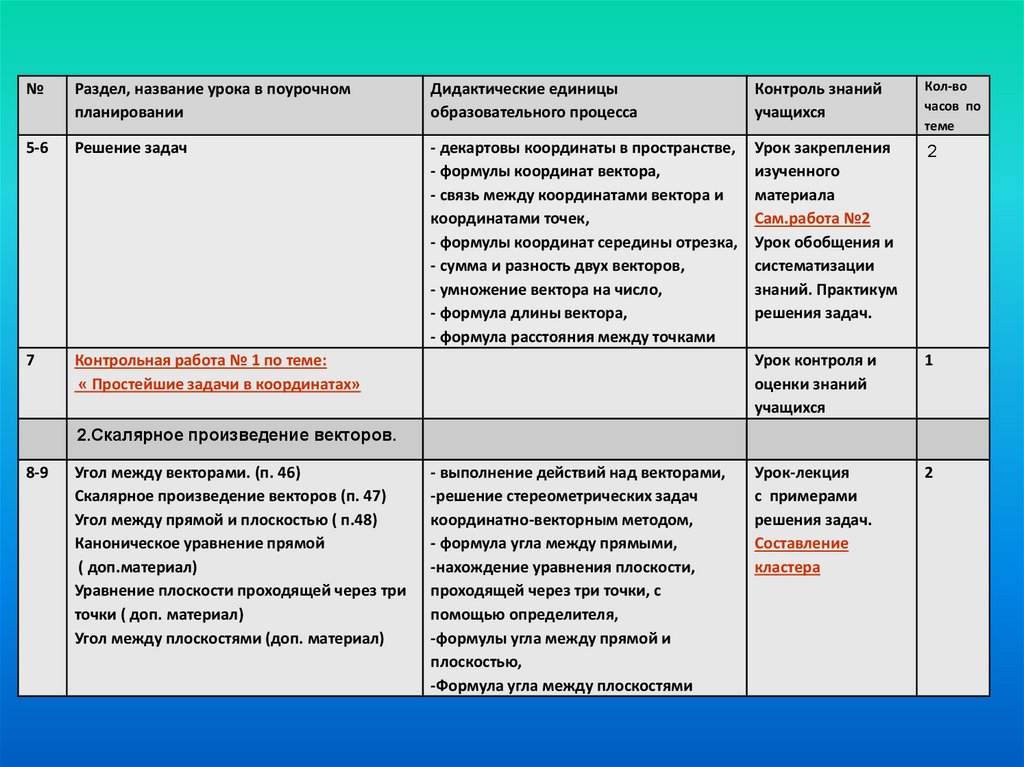
5-6
Решение задач
- декартовы координаты в пространстве,
- формулы координат вектора,
- связь между координатами вектора и
координатами точек,
- формулы координат середины отрезка,
- сумма и разность двух векторов,
- умножение вектора на число,
- формула длины вектора,
- формула расстояния между точками
Урок закрепления
изученного
материала
Сам.работа №2
Урок обобщения и
систематизации
знаний. Практикум
решения задач.
2
7
Контрольная работа № 1 по теме:
« Простейшие задачи в координатах»
Урок контроля и
оценки знаний
учащихся
1
Урок-лекция
с примерами
решения задач.
Составление
кластера
2
2.Скалярное произведение векторов.
8-9
Угол между векторами. (п. 46)
Скалярное произведение векторов (п. 47)
Угол между прямой и плоскостью ( п.48)
Каноническое уравнение прямой
( доп.материал)
Уравнение плоскости проходящей через три
точки ( доп. материал)
Угол между плоскостями (доп. материал)
- выполнение действий над векторами,
-решение стереометрических задач
координатно-векторным методом,
- формула угла между прямыми,
-нахождение уравнения плоскости,
проходящей через три точки, с
помощью определителя,
-формулы угла между прямой и
плоскостью,
-Формула угла между плоскостями

3.

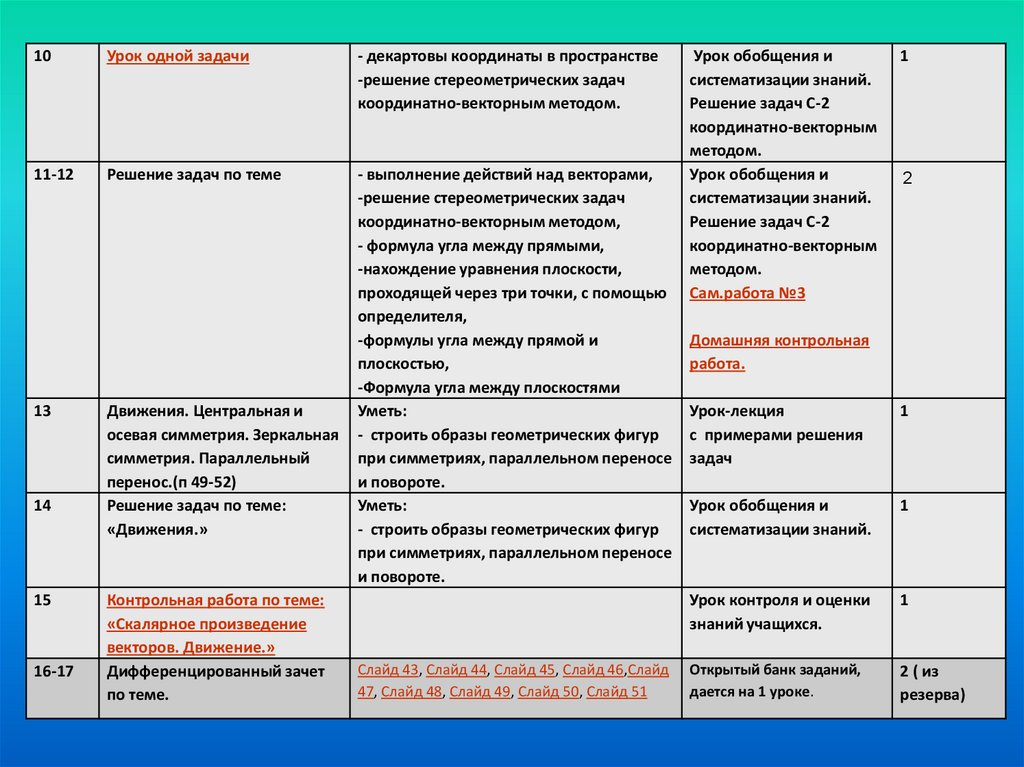
10
Урок одной задачи
- декартовы координаты в пространстве
-решение стереометрических задач
координатно-векторным методом.
11-12
Решение задач по теме
- выполнение действий над векторами,
-решение стереометрических задач
координатно-векторным методом,
- формула угла между прямыми,
-нахождение уравнения плоскости,
проходящей через три точки, с помощью
определителя,
-формулы угла между прямой и
плоскостью,
-Формула угла между плоскостями
Уметь:
- строить образы геометрических фигур
при симметриях, параллельном переносе
и повороте.
Уметь:
- строить образы геометрических фигур
при симметриях, параллельном переносе
и повороте.
13
14
15
16-17
Движения. Центральная и
осевая симметрия. Зеркальная
симметрия. Параллельный
перенос.(п 49-52)
Решение задач по теме:
«Движения.»
Контрольная работа по теме:
«Скалярное произведение
векторов. Движение.»
Дифференцированный зачет
по теме.
Слайд 43, Слайд 44, Слайд 45, Слайд 46,Слайд
47, Слайд 48, Слайд 49, Слайд 50, Слайд 51
Урок обобщения и
систематизации знаний.
Решение задач С-2
координатно-векторным
методом.
Урок обобщения и
систематизации знаний.
Решение задач С-2
координатно-векторным
методом.
Сам.работа №3
1
2
Домашняя контрольная
работа.
Урок-лекция
с примерами решения
задач
1
Урок обобщения и
систематизации знаний.
1
Урок контроля и оценки
знаний учащихся.
1
Открытый банк заданий,
дается на 1 уроке.
2 ( из
резерва)

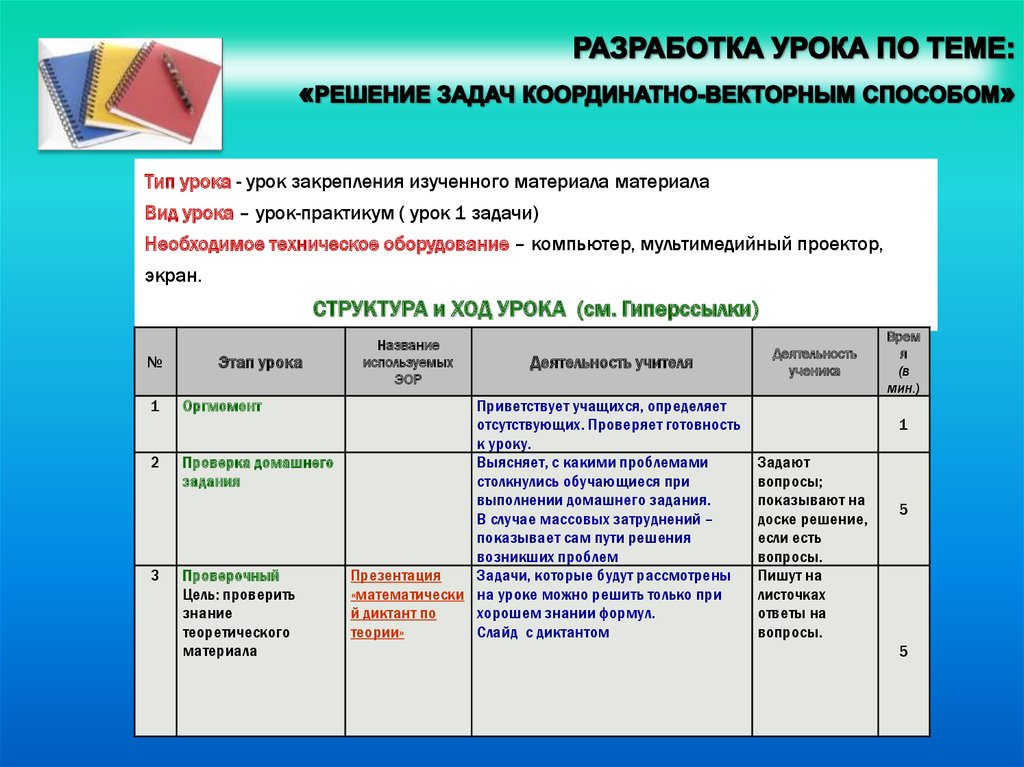
4. Разработка урока по теме «Решение задач координатно-векторным способом» 10 урок в теме: «метод координат в пространстве»

ГЕОМЕТРИЯ 10-11: УЧЕБ. ДЛЯ ОБЩЕОБРАЗОВАТ. УЧРЕЖДЕНИЙ /(Л.С. АТАНАСЯН,
В.Ф.БУТУЗОВ, Л.С. КАДОМЦЕВ И ДР.) – М.: ПРОСВЕЩЕНИЕ, 2009.

5.

Тип урока - урок закрепления изученного материала материала
Вид урока – урок-практикум ( урок 1 задачи)
Необходимое техническое оборудование – компьютер, мультимедийный проектор,
экран.
СТРУКТУРА и ХОД УРОКА (см. Гиперссылки)
№
1
2
3
Этап урока
Оргмомент
Проверка домашнего
задания
Проверочный
Цель: проверить
знание
теоретического
материала
Название
используемых
ЭОР
Деятельность учителя
Приветствует учащихся, определяет
отсутствующих. Проверяет готовность
к уроку.
Выясняет, с какими проблемами
столкнулись обучающиеся при
выполнении домашнего задания.
В случае массовых затруднений –
показывает сам пути решения
возникших проблем
Презентация
Задачи, которые будут рассмотрены
«математически на уроке можно решить только при
й диктант по
хорошем знании формул.
теории»
Слайд с диктантом
Деятельность
ученика
Врем
я
(в
мин.)
1
Задают
вопросы;
показывают на
доске решение,
если есть
вопросы.
Пишут на
листочках
ответы на
вопросы.
5
5

6. СТРУКТУРА и ХОД УРОКА

№
Этап урока
Название
используемых
ЭОР
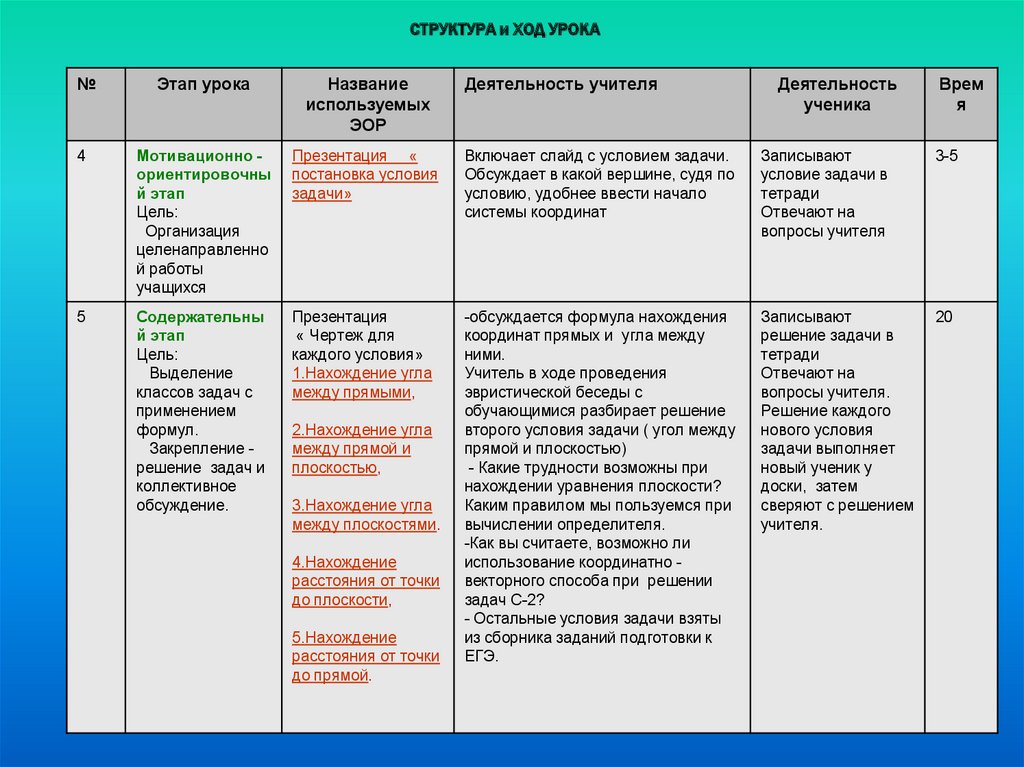
4
Мотивационно ориентировочны
й этап
Цель:
Организация
целенаправленно
й работы
учащихся
Презентация «
постановка условия
задачи»
Включает слайд с условием задачи.
Обсуждает в какой вершине, судя по
условию, удобнее ввести начало
системы координат
Записывают
условие задачи в
тетради
Отвечают на
вопросы учителя
3-5
5
Содержательны
й этап
Цель:
Выделение
классов задач с
применением
формул.
Закрепление решение задач и
коллективное
обсуждение.
Презентация
« Чертеж для
каждого условия»
1.Нахождение угла
между прямыми,
-обсуждается формула нахождения
координат прямых и угла между
ними.
Учитель в ходе проведения
эвристической беседы с
обучающимися разбирает решение
второго условия задачи ( угол между
прямой и плоскостью)
- Какие трудности возможны при
нахождении уравнения плоскости?
Каким правилом мы пользуемся при
вычислении определителя.
-Как вы считаете, возможно ли
использование координатно векторного способа при решении
задач С-2?
- Остальные условия задачи взяты
из сборника заданий подготовки к
ЕГЭ.
Записывают
решение задачи в
тетради
Отвечают на
вопросы учителя.
Решение каждого
нового условия
задачи выполняет
новый ученик у
доски, затем
сверяют с решением
учителя.
20
2.Нахождение угла
между прямой и
плоскостью,
3.Нахождение угла
между плоскостями.
4.Нахождение
расстояния от точки
до плоскости,
5.Нахождение
расстояния от точки
до прямой.
Деятельность учителя
Деятельность
ученика
Врем
я

7.

СТРУКТУРА и ХОД УРОКА
№
6
7
Этап урока
Название
используемых
ЭОР
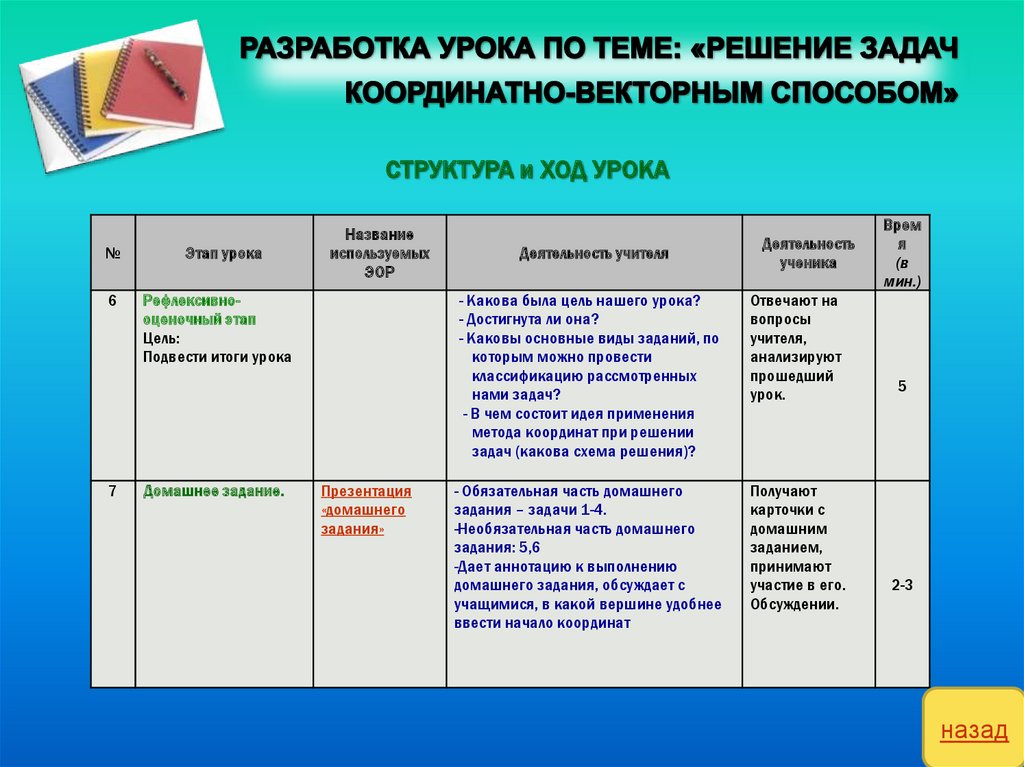
Рефлексивнооценочный этап
Цель:
Подвести итоги урока
Домашнее задание.
Презентация
«домашнего
задания»
Деятельность учителя
Деятельность
ученика
- Какова была цель нашего урока?
- Достигнута ли она?
- Каковы основные виды заданий, по
которым можно провести
классификацию рассмотренных
нами задач?
- В чем состоит идея применения
метода координат при решении
задач (какова схема решения)?
Отвечают на
вопросы
учителя,
анализируют
прошедший
урок.
- Обязательная часть домашнего
задания – задачи 1-4.
-Необязательная часть домашнего
задания: 5,6
-Дает аннотацию к выполнению
домашнего задания, обсуждает с
учащимися, в какой вершине удобнее
ввести начало координат
Получают
карточки с
домашним
заданием,
принимают
участие в его.
Обсуждении.
Врем
я
(в
мин.)
5
2-3
назад

8. Самостоятельная работа № 1

Вариант 1
1. Найти координаты вектора , если А (-1; 3; 2),
В ( 3; -5; -7) и разложить вектор
по
координатным векторам .
Вариант 2
1. Найти координаты вектора , если А (5; 3; -6),
В (- 2; 1; 4) и разложить вектор
по
координатным векторам.
2. Даны А (8; 3: -5) и В (-7; 5; 3)
найти:
а) координаты точки С (x;y;z ), которая
является серединой отрезка АВ
б) длину вектора
;
в) координаты вектора .
2. Даны А (-9; 4; -11) и В (7; - 6; -5)
найти:
а) координаты точки С (x;y;z ), которая
является серединой отрезка АВ ;
б) длину вектора
;
в) координаты вектора
3. Дано: вектор ( 13; -9; 10) и вектор (-12; 4; -6).
Найти: вектор = 2 – 3 и длину вектора
3. Дано: вектор (- 11; 8; 13) и вектор (10; -14; -9)
Найти: вектор = - 2 + 5 и длину вектора
.
назад

9.

Самостоятельная работа № 2
Вариант 1
Вариант 2
1)Дано: (-1;2;0), (2;-3;-2). Найти: = 0,5 +
1) Дано:
( 3; -0,5; -4), (2;0;1). Найти:
=2 –
2) Дано: (-2;1;-4), (3;4;-2)
2) Дано: (1; -3;0), (4;1;2)
Будут ли перпендикулярны векторы и ?
3)Дано: векторы (1;-2;0), (2;1;-3) , (-3;4;1)
Будут ли перпендикулярны векторы
3) Дано: векторы (1;0;1), (3;-1;0) , (1;1;1)
Найти: cos ( - ;^ )
4)Дано: векторы
Найти:
Найти: cos ( + ;^ )
(-2;7;5), (4;-12;-6)
и
.
5)Дано: А(-2;2;4) и В (1;-2;-1), С – середина
4) Дано: векторы
Найти:
(-4;11;-5), (7;-10;-3)
и
5) Дано: А(-5;1;3) и В (1;-4;-2), С – середина
АВ. Вычислить расстояние МС, если
АВ. Вычислить расстояние МС, если
М(-5;6;2).
М(6;-2;4).
6)Дано: (4;2;4),
и ?
( ; ;0) .Найти: (2 ;^0,5 ).
6) Дано: ( ;0;1),
(2;0;2 ). Найти: (3 ;^2 ).
назад

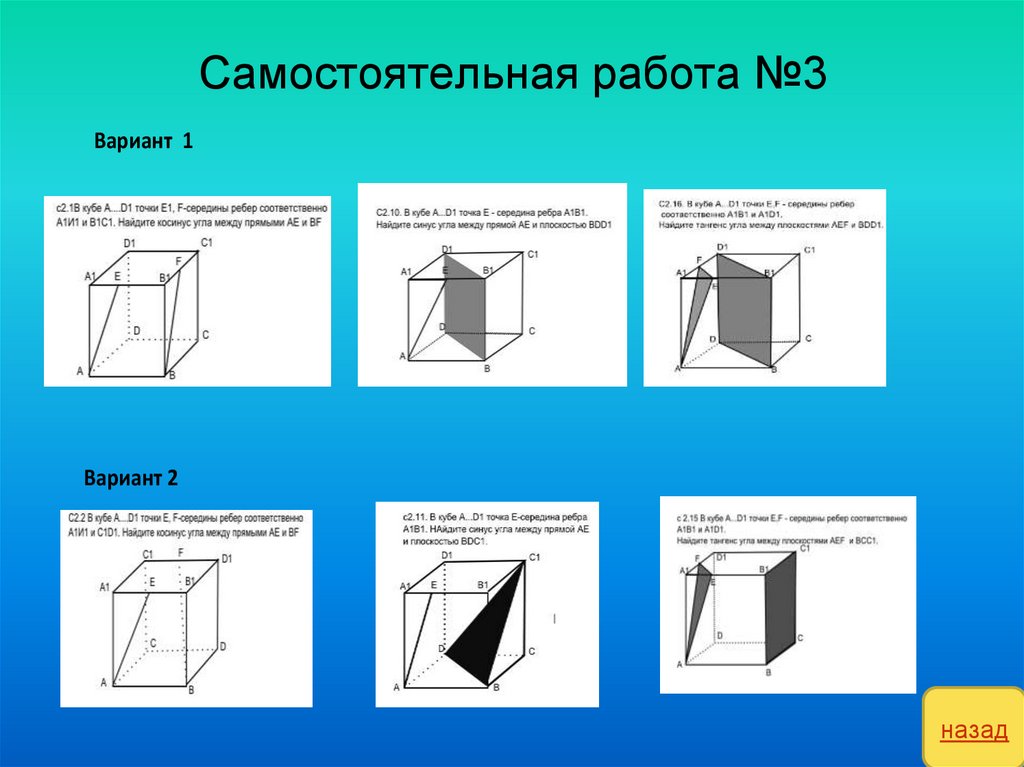
10. Самостоятельная работа №3

Вариант 1
Вариант 2
назад

11. Контрольная работа №1 по теме: «Метод координат в пространстве»

Вариант № 1
1)Вершины треугольника АВС имеют
координаты А(-2;0;1),В(-1;2;3), С(8;-4;9).
Найдите координаты вектора BM , если
ВМ – медиана ∆АВС.
2)Дан вектор b(3;1;-2) и вектор c (1;4;-3)
Найдите: │2b-c│.
3)Даны точки А(-1; 5;3), В(7;-1;3), С(3;-2;6).
Доказать, что ∆АВС – прямоугольный.
4)Даны точки А(-2;1;2), В(-6;3;-2).
На оси аппликат найти точку С,
равноудаленную от точек А и В.
Вариант № 2
1)Вершины треугольника АВС имеют
координаты А(-1;2;3), В(1;0;4), С(3;-2;1).
Найдите координаты вектора AM , если
АМ – медиана ∆АВС.
2)Дан вектор a(5;-1;2), и вектор b (3;2;-4)
Найдите: │a – 2b│
3)Даны точки А(-1; 5;3), В(-1;3;9), С(3;-2;6).
Доказать, что ∆АВС – прямоугольный.
4)Даны точки А(4;5;4), В(2;3;-4).
На оси абсцисс найти точку С,
равноудаленную от точек А и В.
назад

12. Контрольная работа № 2

Вариант № 1
Вариант № 2
1)Вычислите скалярное произведение
векторов m и n , если m= a+2b-c,
n =2a –b, │ā│= 2, │b│=3, (a;^b) = 60.
c a, c b
1)Вычислите скалярное произведение
векторов m и n , если m= 2a – b + c,
n= -a +2b, │ā│=3,│b│=2, (a;^b)= 30
c a , c b .
2)Дан куб АВСDА1В1С1D1. Найдите угол
между прямыми АD1 и ВМ, где М –
середина DD1.
2)Дан куб АВСDА1В1С1D1. Найдите угол
между прямыми АС и D С1.
3) При движении прямая а отображается
на прямую a1 , а плоскость α - на
плоскость α 1. Докажите, что если
а ||α, то а1 || α 1
3) При движении прямая а
отображается на прямую а1, а
плоскость α - на плоскость α 1.
Докажите, что если
а α, то а1 α 1.
назад

13.

Кластер
1. Каноническое уравнение прямой, проходящей
через две точки
А(
), В(
).
3.
Уравнение плоскости, проходящей через три
точки : А(
), В(
), C(
)
A x + By + Cz +D = 0 -- уравнение плоскости.
(
) - коэффициенты прямой.
2. Угол между двумя прямыми
4.
Угол между двумя плоскостями
5. Угол между прямой и плоскостью
6.
Расстояние от точки до плоскости: ρ(A;α)
A(
), Ax +By +Cz +D = 0.
назад

14.

Домашняя контрольная работа
Вариант 1
Вариант 2
В кубе АВСDA1B1C1D1 найдите угол между
прямыми ВА1 и B1D1.
В кубе АВСDA1B1C1D1 найдите угол между
прямыми AB1и BD1.
2. В кубе АВСDA1B1C1D1 найдите синус угла
между прямой А1D1 и плоскостью АСB1
2. В кубе АВСDA1B1C1D1 найдите синус угла
между прямой DD1 и плоскостью АСB1
3. В кубе АВСDA1B1C1D1 найдите косинус
угла между плоскостями AB1D1 и СB1D1
3. В кубе АВСDA1B1C1D1 найдите тангенс угла
между плоскостями ABC и DА1C1
4. В единичном кубе АВСDA1B1C1D1 найдите
расстояние от точки В до плоскости DА1C1
4. В единичном кубе АВСDA1B1C1D1 найдите
расстояние от точки В до плоскости AB1D1
5.В правильной треугольной призме АВСA1B1C1, 5.В правильной треугольной призме АВСA1B1C1,
все ребра которой равны 1, найдите расстояние все ребра которой равны 1, найдите расстояние
между прямыми АА1 и ВС1
между прямыми АА1 и ВС.
6*. Ребро куба равно а. Найдите расстояние
между прямыми, на которых лежат
скрещивающиеся диагонали двух смежных
граней куба.
6*. В единичном кубе АВСDA1B1C1D1 на
диагоналях граней AD1 и D1B1 взяты точки Е и F
так, что D1Е= 1/3АD1, D1F=2/3 B1D1. Найдите
длину отрезка EF.
назад

15. Постановка задачи

Дано: ABCDA1B1C1D1 – куб
Найти :
1) угол между прямыми (АВ1; ^ВD1) - ?
2) угол между прямой А1C и плоскостью
(BC1D)
( A1С; ^ (BC1D) - ?
3) угол между плоскостями (ABC);^(СB1D1)
4) расстояние от точки А до плоскости
(BDA1 )
ρ (A; (BDA1)) - ?
5)расстояние от точки А до прямой ВD1
ρ (A ;BD1) -?
назад

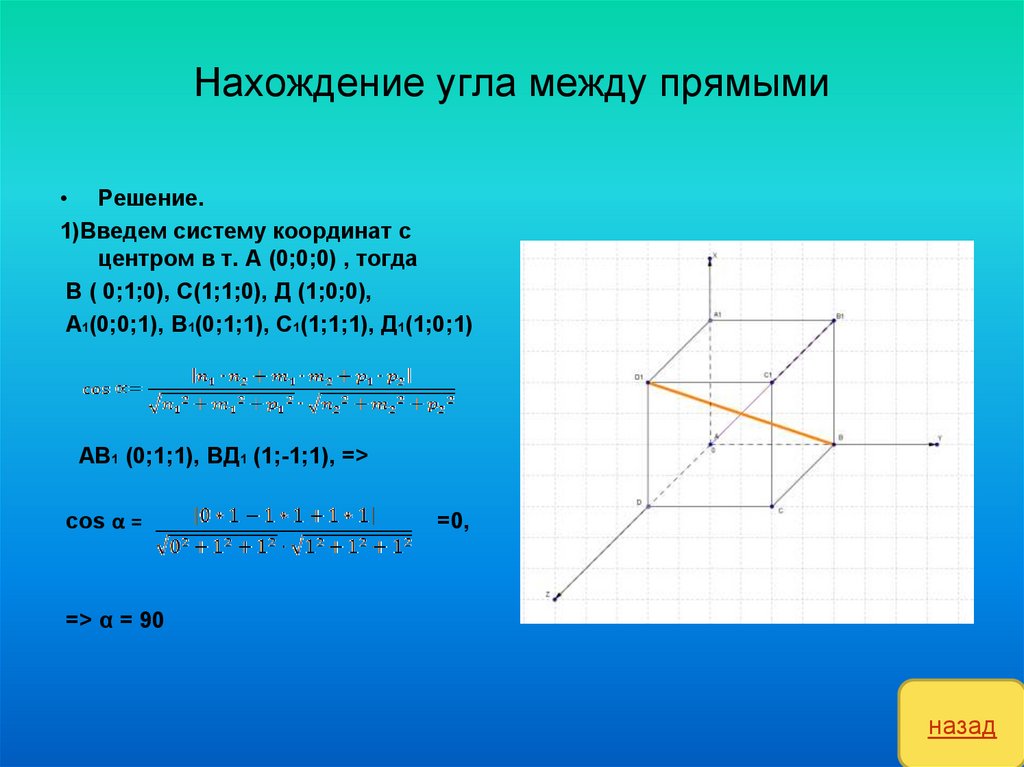
16. Нахождение угла между прямыми

• Решение.
1)Введем систему координат с
центром в т. А (0;0;0) , тогда
В ( 0;1;0), С(1;1;0), Д (1;0;0),
А1(0;0;1), В1(0;1;1), С1(1;1;1), Д1(1;0;1)
АВ1 (0;1;1), ВД1 (1;-1;1), =>
cos α =
=0,
=> α = 90
назад

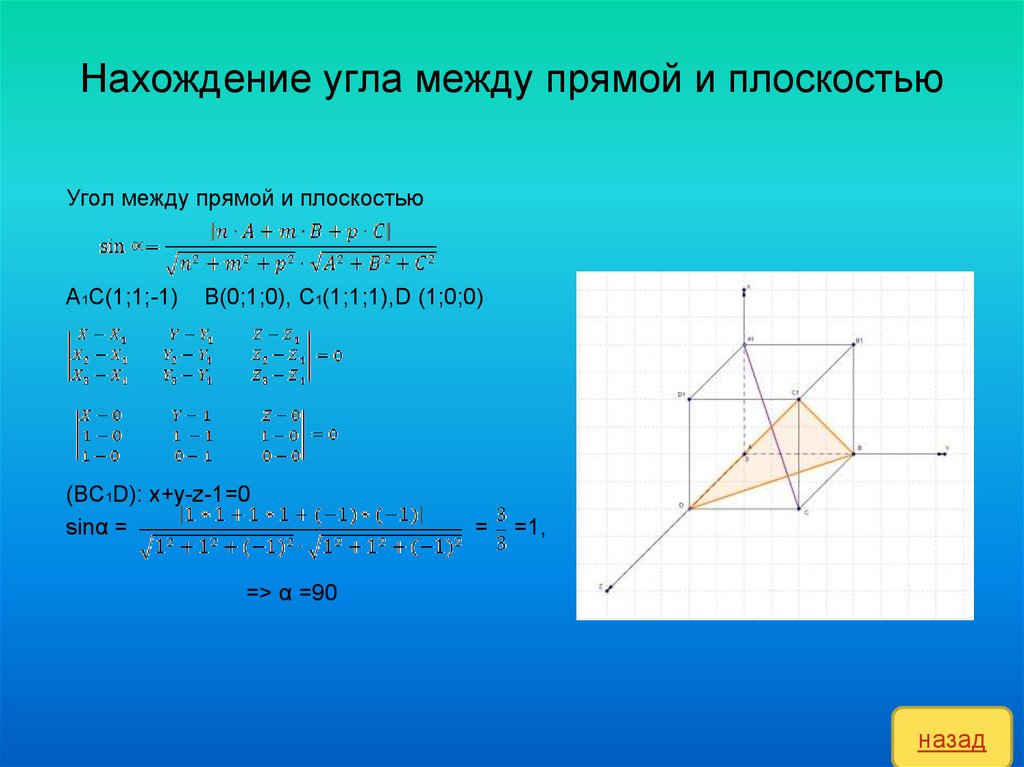
17. Нахождение угла между прямой и плоскостью

Угол между прямой и плоскостью
А1C(1;1;-1)
В(0;1;0), С1(1;1;1),D (1;0;0)
(BC1D): x+y-z-1=0
sinα =
=
=1,
=> α =90
назад

18. Нахождение угла между плоскостями

Угол между двумя плоскостями
cos α
Уравнение плоскости, проходящей
через три точки :
C(1;1;0), В1(0;1;1), D1(1;0;1),
=> (CB1D1) : X+Y+Z-2=0
=> (ABC): -Z=0
=
=> α= arccos
назад

19. Нахождение расстояния от точки до плоскости

Расстояние от точки до плоскости:
ρ(A;α)
A(
), Ax +By +Cz +D = 0.
A(0;0;0) , B(0;1;0),D(1;0;0),A1(0;0;1)
=> (BDA1): -X-Y-Z+1=0
=
=
назад

20. Нахождение расстояния от точки до прямой

ρ (A ;BD1), BD1(1;-1;1), AB(0;1;0), AD1(1;0;1)
│BD1│= , │AD1│= √ 2 , │AB│= 1
(AD1)^(BD1)=α
cos α =
sinα =
=
=
=
=
, =>
=
S = AD1*BD1*sinα =
ρ (A; BD1) =
=
*
*
=
назад

21.

Угол между двумя прямыми
1.В кубе A … D1 найдите углы между прямыми( AB1) и( BD1).
2.В кубе A … D1 найдите углы между прямыми (AA1) и (BD1).
3. В кубе A … D1 найдите углы между прямыми (AB1) и ( BC1).
4. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1, найдите угол между ( AA1) и
(BC1).
5. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1, найдите угол между ( AB) и( A1C).
6. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1, найдите угол между ( AB1) и(
BC1).
7.В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AB1) и( BC 1).
8. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AB1) и( BD1).
9. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AB1) и( BE1).
10. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между (AB1) и( CF1).
11. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AB1) и (BF1).
12. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AB1) и (CD1).
13. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AB1) и( CA1).
14. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AB1) и (DF1).
15. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AC1) и (BD1).
16. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между (AB1) и (DA1).
17. В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AC1) и (BE1).
назад

22.

Угол между прямой и плоскостью
1.В кубе A…D1 найдите угол между прямой AB1 и плоскостью ABC1.
2. В кубе A…D1 найдите угол между прямой AС1 и плоскостью BCC1.
3. В кубе A…D1 найдите угол между прямой AB1 и плоскостью BC1D.
4. В кубе A…D1 найдите угол между прямой AС1 и плоскостью BB1D1.
5. В кубе A…D1 найдите угол между прямой AС1 и плоскостью BA1D.
6. В правильной треугольной призме ABCA1B1C1 , все ребра которой равны 1, найдите угол между прямой АА1 , и
плоскостью ABC1.
7. В правильной треугольной призме ABCA1B1C1 , все ребра которой равны 1, найдите угол между прямой АB , и
плоскостью A1BC1.
8. В правильной треугольной призме ABCA1B1C1 , все ребра которой равны 1, найдите угол между прямой АA1 , и
плоскостью AB1C1.
9. В правильной треугольной призме ABCA1B1C1 , все ребра которой равны 1, найдите угол между прямой АB1 , и
плоскостью BB1C1.
10.В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой AC1 и ABC.
11. В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой AB1 и ABD1.
12.В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой BC1 и BDE1.
13.В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой AB1 и ABC1.
14. В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой AA1 и ACE1.
15. В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой AB1 и ACE1.
16. В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой AB1 и ADE1.
17. В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой AC1 и ADE1.
назад

23.

Угол между двумя плоскостями
1. В кубе A…D1 найдите углы между плоскостями ABC и AB1D1.
2. В кубе A…D1 найдите углы между плоскостями ACC1 и BDD1.
3. В кубе A…D1 найдите углы между плоскостями ABC1 и BB1D1.
4. В кубе A…D1 найдите углы между плоскостями BC1D1 и BA1D.
5. В кубе A…D1 найдите углы между плоскостями BC1D и BA1D.
6.В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1,найдите угол между плоскостями ABC
и A1B1C.
7. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1,найдите угол между плоскостями ABC
и ACB1.
8. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1,найдите угол между плоскостями
ACB1 и A1C1B.
9.B правильной шестиугольной призме A…F1, ребра которой равны 1, найдите угол между плоскостями ABB1 и
CDD1.
10. B правильной шестиугольной призме A…F1, ребра которой равны 1, найдите угол между плоскостями ACC1 и
CDD1.
11. B правильной шестиугольной призме A…F1, ребра которой равны 1, найдите угол между плоскостями ACC1 и
CEE1.
12. B правильной шестиугольной призме A…F1, ребра которой равны 1, найдите угол между плоскостями CDE1 и
AFE1.
13. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите угол между плоскостями CDF1 и
AFD1.
14. B правильной шестиугольной призме A…F1,ребра которой равны 1,найдите угол между плоскостями BCD1 и
AFE1.
назад

24.

Расстояние от точки до плоскости
1.В единичном кубе A … D1 найдите расстояние от точки A до плоскости BСD1.
2. В единичном кубе A … D1 найдите расстояние от точки A до плоскости CDA1.
3. В единичном кубе A … D1 найдите расстояние от точки A до плоскости BDA1.
4. В единичном кубе A … D1 найдите расстояние от точки A до плоскости CB1D1.
5. В единичном кубе A … D1 найдите расстояние от точки A до плоскости BC1D.
6. В единичном кубе A … D1 найдите расстояние от точки A до плоскости BA1C1.
7. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1 , найдите расстояние от точки A до
плоскости BB1C1.
8. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1 , найдите расстояние от точки A до
плоскости A1B1C1.
9. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1 , найдите расстояние от точки A до
плоскости A1C1B1.
10. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
плоскости BEE1.
11. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
плоскости BFF1.
12. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
плоскости CFF1.
13. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
плоскости BA1E1.
14. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
плоскости A1B1D1.
15. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
плоскости A1B1C1.
16. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
плоскости F1C1D.
назад

25.

Расстояние между двумя прямыми
1. В единичном кубе A … D1 найдите расстояние между прямыми AA1 и BC1.
2. В единичном кубе A … D1 найдите расстояние между прямыми AA1 и BD1.
3. В единичном кубе A … D1 найдите расстояние между прямыми AB1 и CD1.
4. В единичном кубе A … D1 найдите расстояние между прямыми AB1 и BD1.
5. В единичном кубе A … D1 найдите расстояние между прямыми AB1 и BC1.
6. В единичном кубе A … D1 найдите расстояние между прямыми AB1 и A1C1.
7. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1 , найдите расстояние между
прямыми AA1 и BC.
8. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1 , найдите расстояние между
прямыми AA1 и BC1.
9. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1 , найдите расстояние между
прямыми AB и A1C1.
10. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1 , найдите расстояние между
прямыми AB и A1C.
11. В правильной треугольной призме ABCA1B1C1,все ребра которой равны 1 , найдите расстояние между
прямыми AB1 и BC1.
12. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние между прямыми AB1 и
DE1.
13. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние между прямыми AB1 и
BD1.
14. B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние между прямыми AB1 и
BE1.
назад

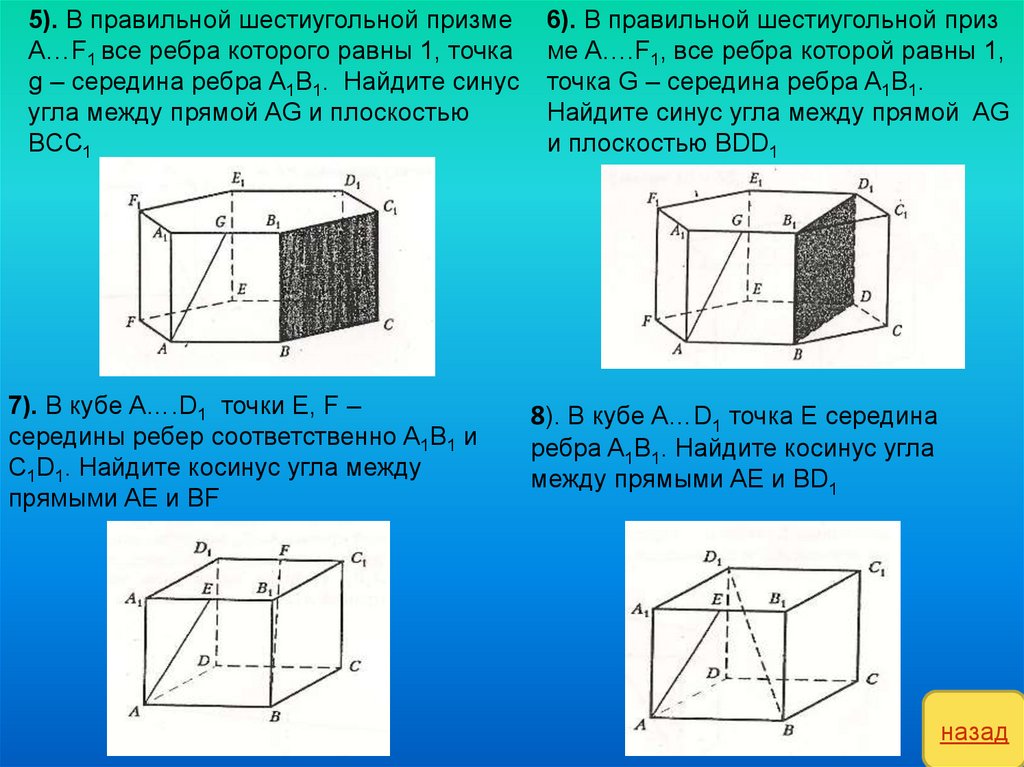
26.

1). В правильной шестиугольной
призмеA…F1 все ребра которой равны
1, точка G - середина ребра A1B1.
Найдите косинус угла между прямыми
AG и BC1
2). В правильной шестиугольной призме
A….F1 все ребра которой равны 1, точка
G – середина ребра A1B1. Найдите
косинус угла между прямыми AG и BD1
3). В кубе A…D1 точка E – середина
ребра A1B1. Найдите синус угла
между прямой AE и плоскостью
BDD1.
4). В кубе A…D1 точка E – середина
ребра A1B1. Найдите синус угла между
прямой AE и плоскостью BDD1.
назад

27.

5). В правильной шестиугольной призме
A…F1 все ребра которого равны 1, точка
g – середина ребра A1B1. Найдите синус
угла между прямой AG и плоскостью
BCC1
7). В кубе A….D1 точки E, F –
середины ребер соответственно A1B1 и
C1D1. Найдите косинус угла между
прямыми AE и BF
6). В правильной шестиугольной приз
ме A….F1, все ребра которой равны 1,
точка G – середина ребра A1B1.
Найдите синус угла между прямой AG
и плоскостью BDD1
8). В кубе A…D1 точка E середина
ребра A1B1. Найдите косинус угла
между прямыми AE и BD1
назад

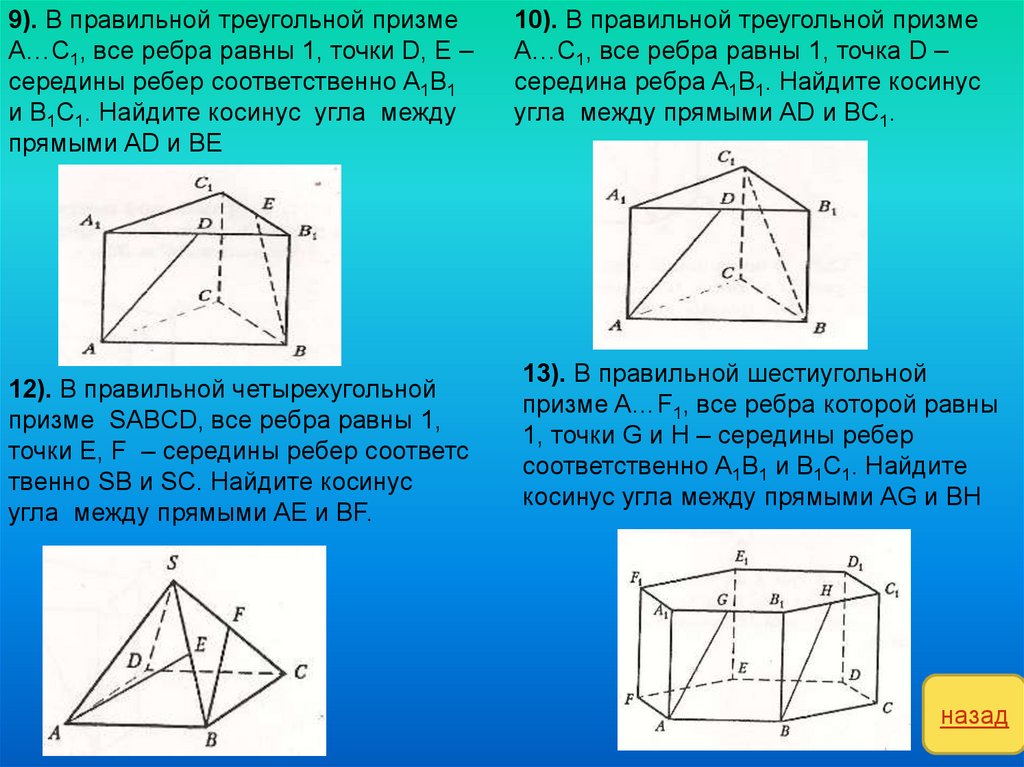
28.

9). В правильной треугольной призме
A…C1, все ребра равны 1, точки D, E –
середины ребер соответственно A1B1
и B1C1. Найдите косинус угла между
прямыми AD и BE
12). В правильной четырехугольной
призме SABCD, все ребра равны 1,
точки E, F – середины ребер соответс
твенно SB и SC. Найдите косинус
угла между прямыми AE и BF.
10). В правильной треугольной призме
A…C1, все ребра равны 1, точка D –
середина ребра A1B1. Найдите косинус
угла между прямыми AD и BC1.
13). В правильной шестиугольной
призме A…F1, все ребра которой равны
1, точки G и H – середины ребер
соответственно A1B1 и B1C1. Найдите
косинус угла между прямыми AG и BH
назад

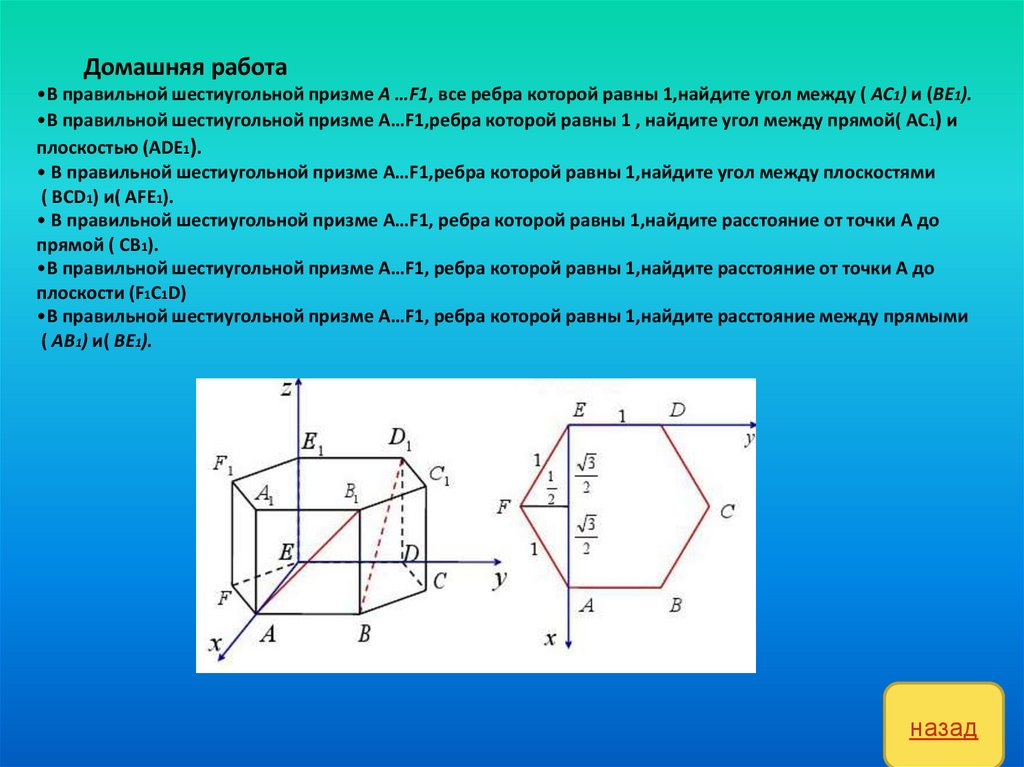
29.

Домашняя работа
•В правильной шестиугольной призме A …F1, все ребра которой равны 1,найдите угол между ( AC1) и (BE1).
•В правильной шестиугольной призме A…F1,ребра которой равны 1 , найдите угол между прямой( AC1) и
плоскостью (ADE1).
• B правильной шестиугольной призме A…F1,ребра которой равны 1,найдите угол между плоскостями
( BCD1) и( AFE1).
• B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
прямой ( CB1).
•B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние от точки A до
плоскости (F1C1D)
•B правильной шестиугольной призме A…F1, ребра которой равны 1,найдите расстояние между прямыми
( AB1) и( BE1).
назад