Алгебраические критерии устойчивости. Качество регулирования

1.

РАДИОАВТОМАТИКА
Лекция 6
АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ
УСТОЙЧИВОСТИ
КАЧЕСТВО РЕГУЛИРОВАНИЯ

2. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ

Алгебраические критерии задают требования к коэффициентам
характеристического полинома, при которых система является
устойчивой.
Необходимое условие устойчивости: Все коэффициенты
характеристического полинома должны быть одного знака
Док-во:
n
anpn+an – 1pn – 1+…+a0=an ∏(p – pi) =
i=1
pi= – αi ,
pi= – αi ± jβi
=an∏(p + αi) ∏(p + αi – jβi) ∏(p + αi + jβi) =
i
i
i
i
i
=an∏(p + αi) ∏[(p + αi)2 + βi2)].
Знака «-» в этом выражении нет, поэтому все коэффициенты
будут того же знака, что и an
Критерий Гурвица: Линейная система устойчива, если
при положительном an все определители Гурвица
положительны.

3.

Матрица Гурвица:
an 1
an 3
an
an 2
0 0
an 1
an 5
an 4
an 3
0
0
0
a0
Определители Гурвица
k-го порядка
получаются
отчеркиванием k
строк и k столбцов
в матрице Гурвица:
Система неравенств: a > 0,
n
Δ1= an-1> 0,
an 1
an
an 3
an 1
an 2
an
3 an 3
an 5
an 2
an 4
2
…
Δn > 0,
0,
0
an 1 0,
an 3

4.

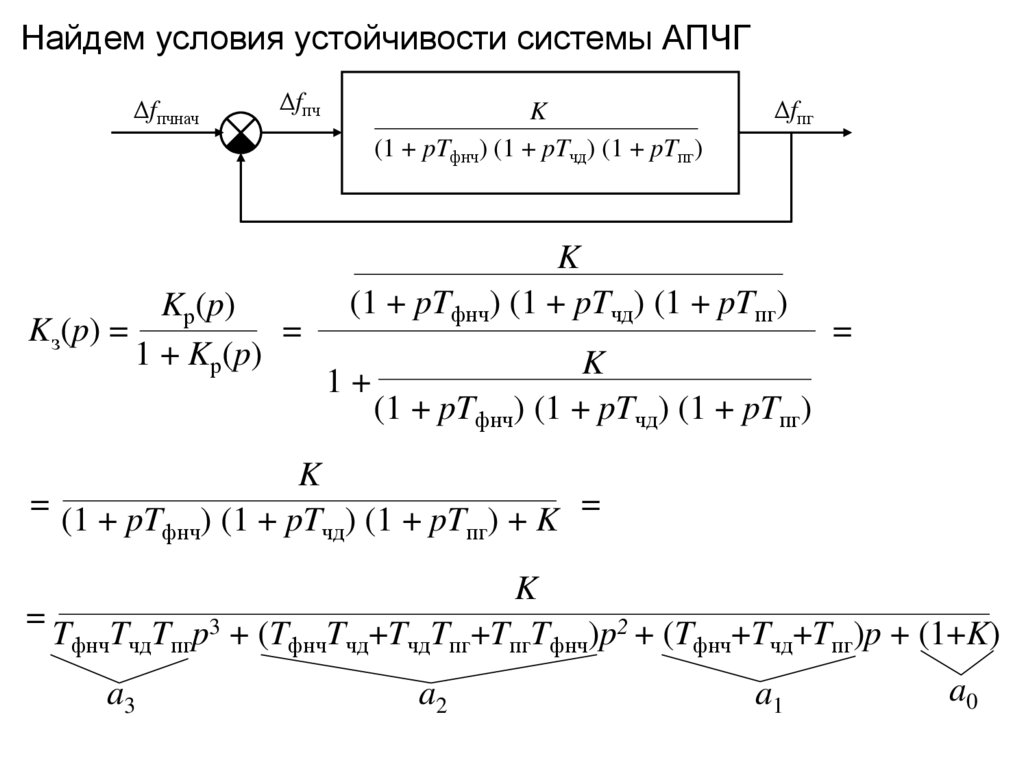
Найдем условия устойчивости системы АПЧГ
Δfпчнач
Δfпч
Kр(p)
Kз(p) =
=
1 + Kр(p)
K
(1 + pTфнч) (1 + pTчд) (1 + pTпг)
Δfпг
K
(1 + pTфнч) (1 + pTчд) (1 + pTпг)
=
K
1+
(1 + pTфнч) (1 + pTчд) (1 + pTпг)
K
= (1 + pT ) (1 + pT ) (1 + pT ) + K =
фнч
чд
пг
K
= T T T p3 + (T T +T T +T T )p2 + (T +T +T )p + (1+K)
фнч чд пг
фнч чд
чд пг
пг фнч
фнч
чд
пг
a3
a2
a1
a0

5.

Матрица Гурвица:
a2
a0
0
a3
a1
0
0
a2
a0
Система неравенств:
1) a3 = TфнчTчдTпг > 0
выполняется всегда.
2) Δ1 = a2 = TфнчTчд+TчдTпг+TпгTфнч > 0
3) Δ2 =
a2
a3
a0
a1
выполняется всегда.
= a1a2 – a0a3 > 0.
(Tфнч+Tчд+Tпг) (TфнчTчд+TчдTпг+TпгTфнч) – (1+K) TфнчTчдTпг > 0.
1
1
1
(Tфнч+Tчд+Tпг) ( T + T + T ) – (1+K) > 0.
пг
фнч
чд
1
1
1
K < (Tфнч+Tчд+Tпг) (T + T + T ) –1.
пг
фнч
чд

6.

Запишем это соотношение для двух крайних случаев
3
а) Tфнч=Tчд=Tпг= T
K < 3T
– 1 = 8.
T
б) Tфнч>>Tчд>>Tпг
a2
4) Δ3 = a0
0
a3
a1
0
1
Тфнч
K < Tфнч
–1≈
.
Tпг
Tпг
0
a2
a2 a0
a0
a0
a3
0 a0 0
a1
1 + K > 0, Это требование означает, что обратная связь должна
быть отрицательной (K > 0) или положительной с
K > –1.
коэффициентом передачи, меньшим 1 (0 > K > –1)
Итак:
1
1
1
–1< K < (Tфнч+Tчд+Tпг) ( T + T + T ) –1.
пг
фнч
чд

7. КАЧЕСТВО РЕГУЛИРОВАНИЯ

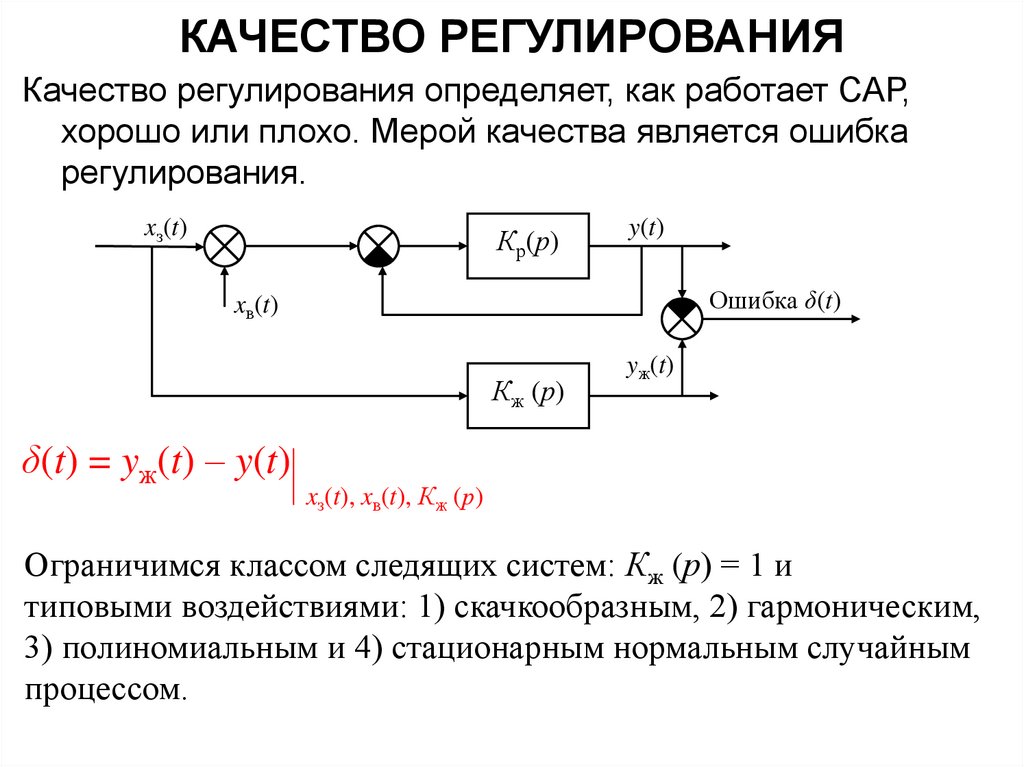
Качество регулирования определяет, как работает САР,
хорошо или плохо. Мерой качества является ошибка
регулирования.
xз(t)
Кр(р)
y(t)
Ошибка δ(t)
xв(t)
Кж (р)
δ(t) = yж(t) – y(t)
yж(t)
xз(t), xв(t), Кж (р)
Ограничимся классом следящих систем: Кж (р) = 1 и
типовыми воздействиями: 1) скачкообразным, 2) гармоническим,
3) полиномиальным и 4) стационарным нормальным случайным
процессом.

8.

1) Качество отработки быстро изменяющихся воздействий.
xз(t) = 1(t), xв(t) = 0.
(t) = 1(t) – hз(t).
Обычно мерой качества является сама переходная характеристика
замкнутой системы hз(t).
2) Качество отработки периодических воздействий.
xз(t) = Asinωt, xв(t) = 0.
(t) = Asinωt– AKз(ω)sin(ωt +φз(ω)).
Мерой качества является комплексная частотная характеристика замкнутой
системы.
Ошибка равна нулю, если Kз(ω) = 1 и φз(ω) = 0.
3) Качество отработки медленно изменяющихся воздействий.
xз(t) = a0 + a1t + a2t2 + …, xв(t) = 0.
Ошибки определяются для первых трех слагаемых полинома и соответственно
называются: статической, скоростной и по ускорению.
3) Качество отработки случайных воздействий.
xз(t) и xв(t) – стационарные нормальные случайные процессы..
Мерой качества является дисперсия ошибки.