Похожие презентации:
Частотный критерий устойчивости Найквиста. Запасы устойчивости ЛСС (лекция 6)
1.
Автоматика и управлениеТема 5. Устойчивость ЛСС
Лекция 6. Частотный критерий устойчивости Найквиста. Запасы
устойчивости ЛСС. Области устойчивости в пространстве
параметров АС
2.
5.7. Частотный критерий устойчивости Найквиста (1932 г.)1. Не требует знания передаточной функции замкнутой АС, т.к.
позволяет исследовать устойчивость замкнутой АС по ЛЧХ
разомкнутой системы.
2. Позволяет исследовать устойчивость систем, включающих
звенья постоянного запаздывания.
Использование данного критерия базируется на знании
передаточной функции разомкнутой системы, определении
числа нейтральных vp и числа неустойчивых p полюсов
разомкнутой системы, а также построении годографа W(j )
и определении полного угла поворота N радиус-вектора
функции Найквиста N(j ), определяемой равенством:
N(j ) = 1 + W(j ),
при изменении частоты от 0 до .
3.
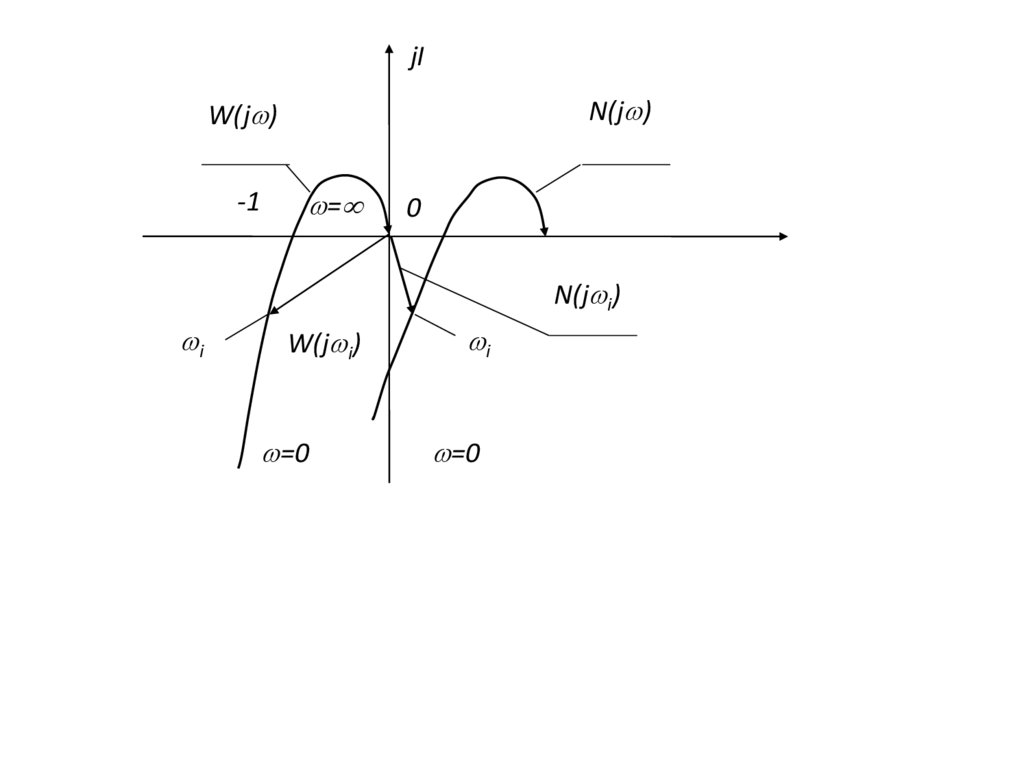
jIN(j )
W(j )
-1
=
0
N(j i)
i
W(j i)
=0
i
=0
4.
Годограф W(j ), дополненный дугой бесконечно большогорадиуса, иногда называют "замкнутым годографом"
разомкнутой системы W(p).
W(j )
jI
jI
=0
=
=0
R
W(j )
W(j )
=
jI
=
R
R
=0
5.
Формулировка критерия НайквистаОдномерная замкнутая ЛСС устойчива, если угол
поворота вектор-функции Найквиста N(j ), при изменении
частоты от 0 до , равен:
N ( v p 2 p )
2
где vp, p - число нейтральных и неустойчивых корней
характеристического полинома разомкнутой системы.
При этом полагается, что W(p) рационального вида и,
следовательно, степени характеристических полиномов
разомкнутой и замкнутой систем совпадают
6.
Критерий Найквиста для систем устойчивых илинейтральных в разомкнутом состоянии
Следствие №1.
Для ЛСС устойчивых или нейтральных в разомкнутом
состоянии, замкнутая АС будет устойчивой, если годограф
АФЧХ разомкнутой системы не охватывает точку с
координатами (-1, j0).
7.
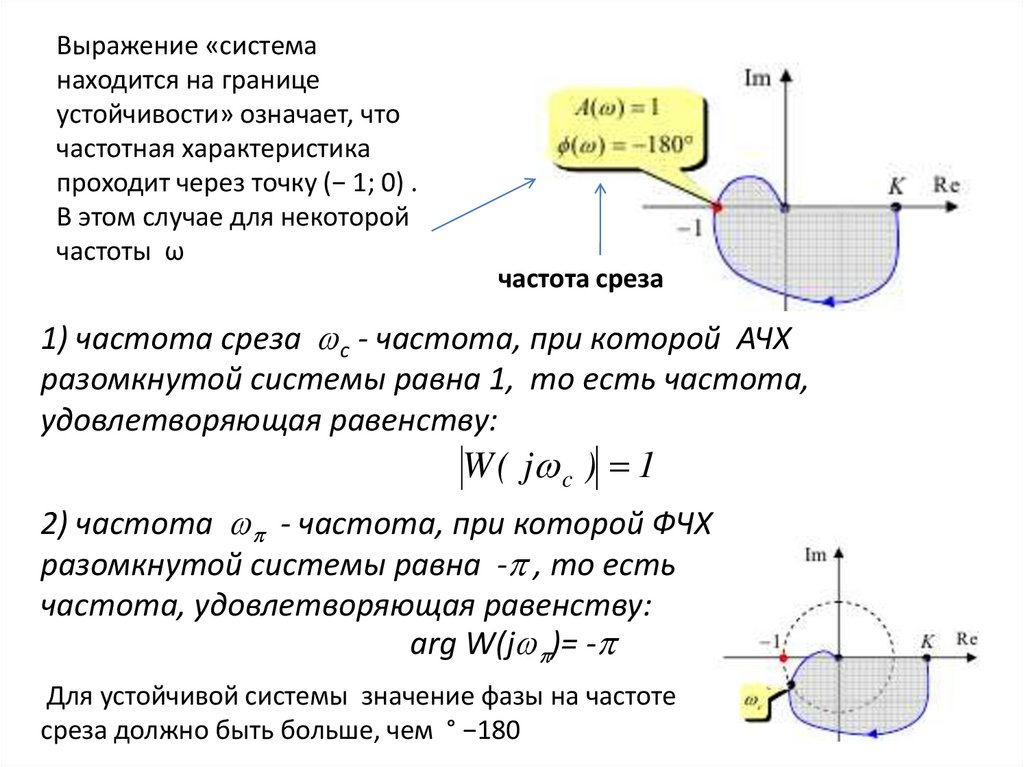
Выражение «системанаходится на границе
устойчивости» означает, что
частотная характеристика
проходит через точку (− 1; 0) .
В этом случае для некоторой
частоты ω
частота среза
1) частота среза с - частота, при которой АЧХ
разомкнутой системы равна 1, то есть частота,
удовлетворяющая равенству:
W ( j c ) 1
2) частота - частота, при которой ФЧХ
разомкнутой системы равна - , то есть
частота, удовлетворяющая равенству:
arg W(j )= -
Для устойчивой системы значение фазы на частоте
среза должно быть больше, чем ° −180
8.
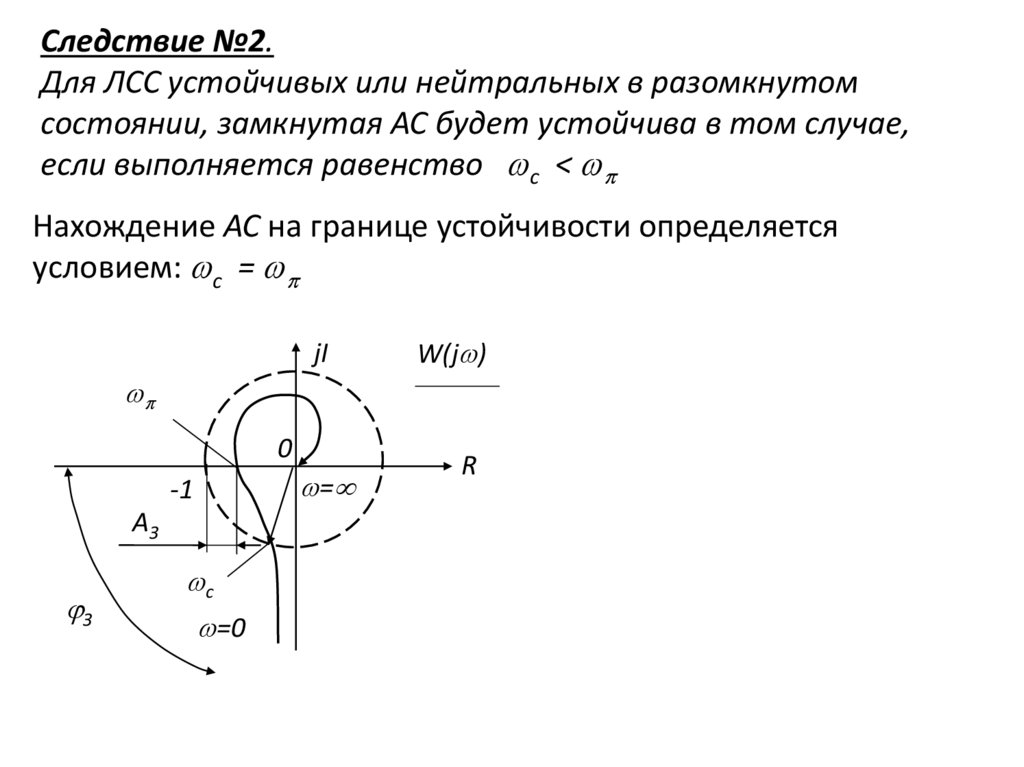
Следствие №2.Для ЛСС устойчивых или нейтральных в разомкнутом
состоянии, замкнутая АС будет устойчива в том случае,
если выполняется равенство с <
Нахождение АС на границе устойчивости определяется
условием: с =
jI
W(j )
=
R
0
-1
AЗ
З
c
=0
9.
Анализ устойчивости ЛСС с помощью ЛЧХразомкнутой системы.
Следствие № 2 часто называют логарифмическим
критерием Найквиста
На практике для определения частот с и удобней применять
логарифмические частотные характеристики
Эти частоты определяются по графикам ЛЧХ и удовлетворяют равенствам:
L( с ) = 20lgWа(w ) = 20lg1 = 0,
( ) = - .
10.
L,ДбL( )
-20
40
( )
LЗ
-20
с
10
1
замкнутая АС устойчива
-40
20
0,1
c < , следовательно,
1000
100
,c -1
-60
-
40
З
В общем случае частот , для которых ( )= - , может быть несколько
Замкнутая АС устойчива, если число частот , для которых
L( )>0, равно 0 или четное.
11.
Неминимальнофазовыми - называются системы,передаточная функция W(p) которых в разомкнутом
состоянии имеет полюсы или нули в правой части
комплексной плоскости.
Системы, у которых W(p) не имеют полюсов и нулей с
положительными вещественными частями, именуются
минимальнофазовыми.
Следовательно, системы неустойчивые в разомкнутом
состоянии, являются неминимальнофазовыми.
12.
Оба следствия критерия Найквиста справедливы дляминимально-фазовых в разомкнутом состоянии систем, т.е.
таких систем, которые удовлетворяют условиям:
•Нули и полюса W(p) располагаются в левой полуплоскости;
•АЧХ – Wа( ) монотонно убывает.
Если W(p) имеет полюса с положительной вещественной частью
(разомкнутая система неустойчива):
1-й вариант - нужно считать, сколько раз годограф пересекает
ось абсцисс левее точки (-1;0) . Причем переходы «сверху вниз»
считаются положительными, а переходы «снизу вверх» отрицательными.
Для того, чтобы замкнутая система была устойчива,
необходимо и достаточно, чтобы разница между числом
положительных и отрицательных переходов была равна
l/2 , где l – число неустойчивых полюсов функции W(p)
13.
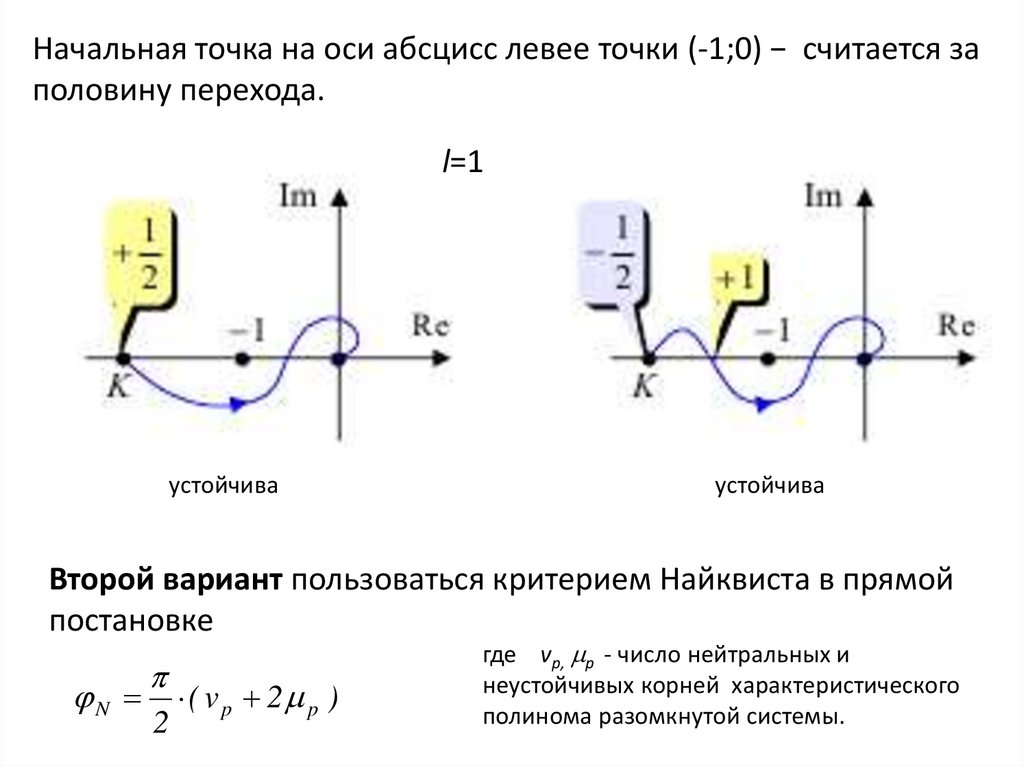
Начальная точка на оси абсцисс левее точки (-1;0) − считается заполовину перехода.
l=1
устойчива
устойчива
Второй вариант пользоваться критерием Найквиста в прямой
постановке
N
2
( v p 2 p )
где vp, p - число нейтральных и
неустойчивых корней характеристического
полинома разомкнутой системы.
14.
С развитием и внедрением в практику ЭВМ, дляисследования АС на устойчивость стало возможным активно
использовать метод непосредственного определения корней
А(р)=0 с целью изображения траекторий их перемещений
при изменении параметров АС. Этот метод получил название
корневого годографа и является базовым в США для
исследования устойчивости и определения запасов
устойчивости АС
15.
Влияние коэффициента усиления разомкнутой системы наустойчивость замкнутой АС
Представим АФЧХ разомкнутой АС в виде:
W(j ) = K W1 (j ),
где K - общий коэффициент усиления разомкнутой АС.
K3
K2
K1
π
K1 < K 2 < K 3
=0
=
R
16.
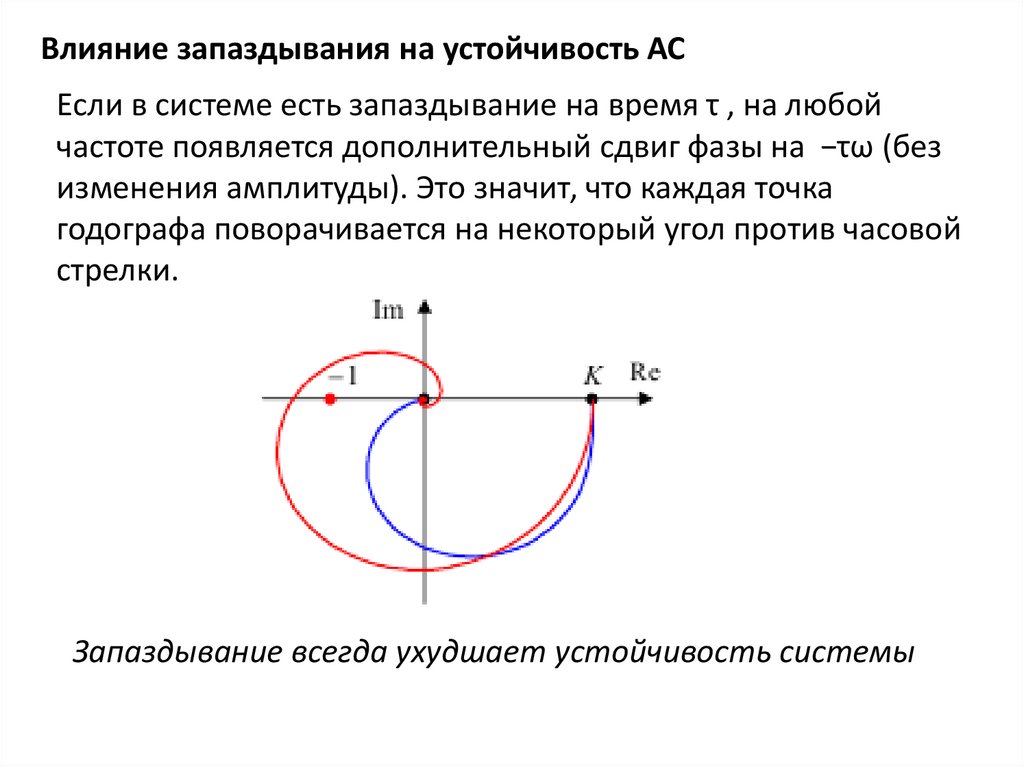
Влияние запаздывания на устойчивость АСЕсли в системе есть запаздывание на время τ , на любой
частоте появляется дополнительный сдвиг фазы на −τω (без
изменения амплитуды). Это значит, что каждая точка
годографа поворачивается на некоторый угол против часовой
стрелки.
Запаздывание всегда ухудшает устойчивость системы
17.
5.8. Запасы устойчивости ЛССПри проектировании АС, необходимо предусмотреть некоторый "запас
устойчивости", характеризующий удаленность АС от границы
устойчивости и часто называемый степенью ее устойчивости.
1. Запас устойчивости по фазе 3 - неотрицательная
величина, определяемая равенством:
3 = + argW(j с ) = + ( с ),
где ( с ) - величина ФЧХ разомкнутой АС на частоте с
Запас устойчивости по фазе - это угол, на который необходимо
довернуть ФЧХ разомкнутой АС, чтобы вывести замкнутую систему
на границу устойчивости.
2. Запас устойчивости по амплитуде L3 неотрицательная величина, определяемая равенством:
L3 = |20lgWa ( )| = |L( )|,
где L( )- значение ЛАХ разомкнутой АС на частоте
Запас устойчивости по амплитуде L3 - это та величина на которую
необходимо увеличить коэффициент усиления разомкнутой АС, чтобы
вывести замкнутую систему на границу устойчивости.
18.
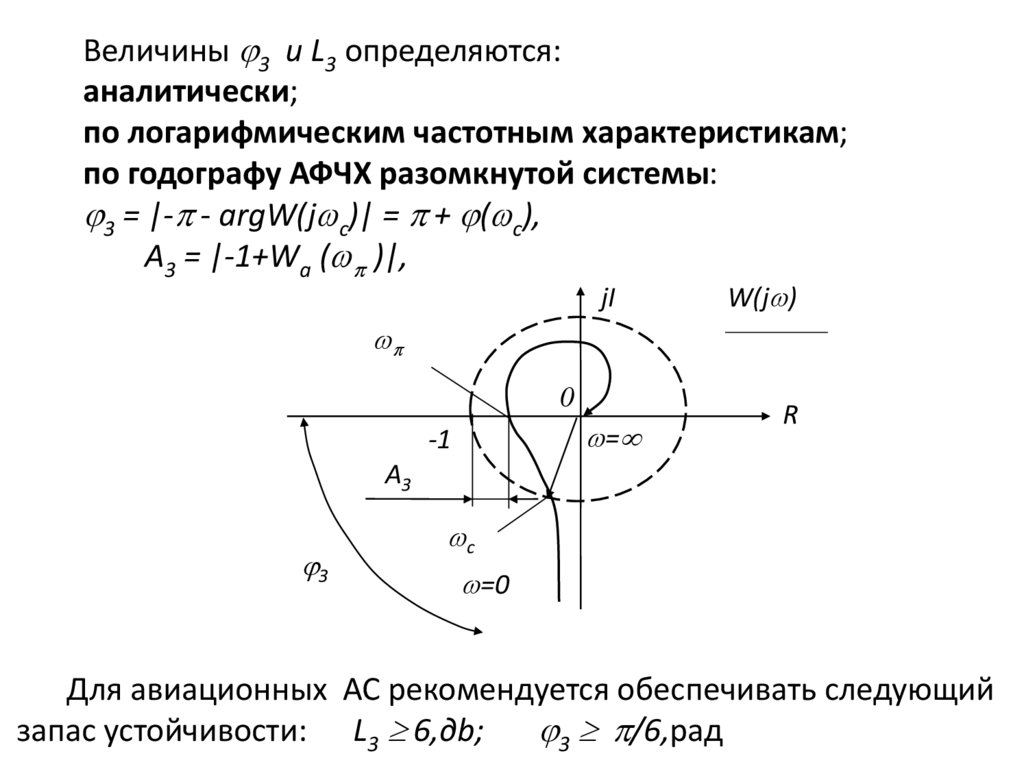
Величины 3 и L3 определяются:аналитически;
по логарифмическим частотным характеристикам;
по годографу АФЧХ разомкнутой системы:
3 = |- - argW(j с)| = + ( с),
A3 = |-1+Wа ( )|,
jI
W(j )
0
=
-1
R
AЗ
З
c
=0
Для авиационных АС рекомендуется обеспечивать следующий
запас устойчивости: L3 6,дb;
3 /6,рад
19.
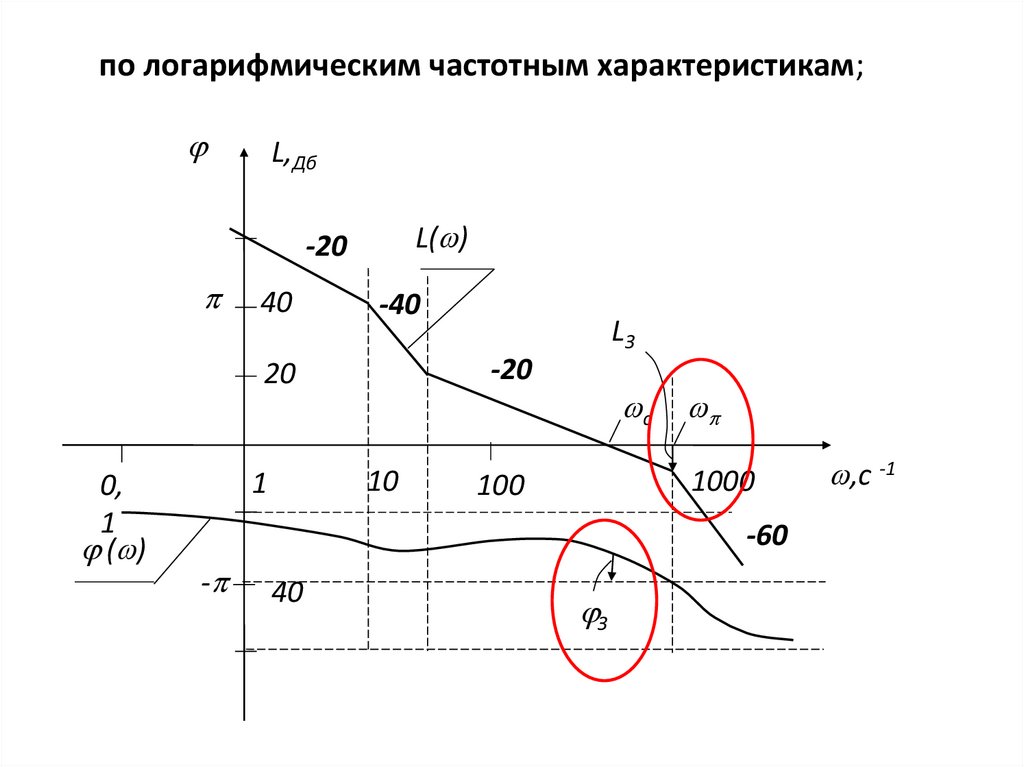
по логарифмическим частотным характеристикам;L,Дб
L( )
-20
40
-40
-20
20
0,
1
( )
10
1
LЗ
с
1000
100
-60
-
40
З
,c -1
20.
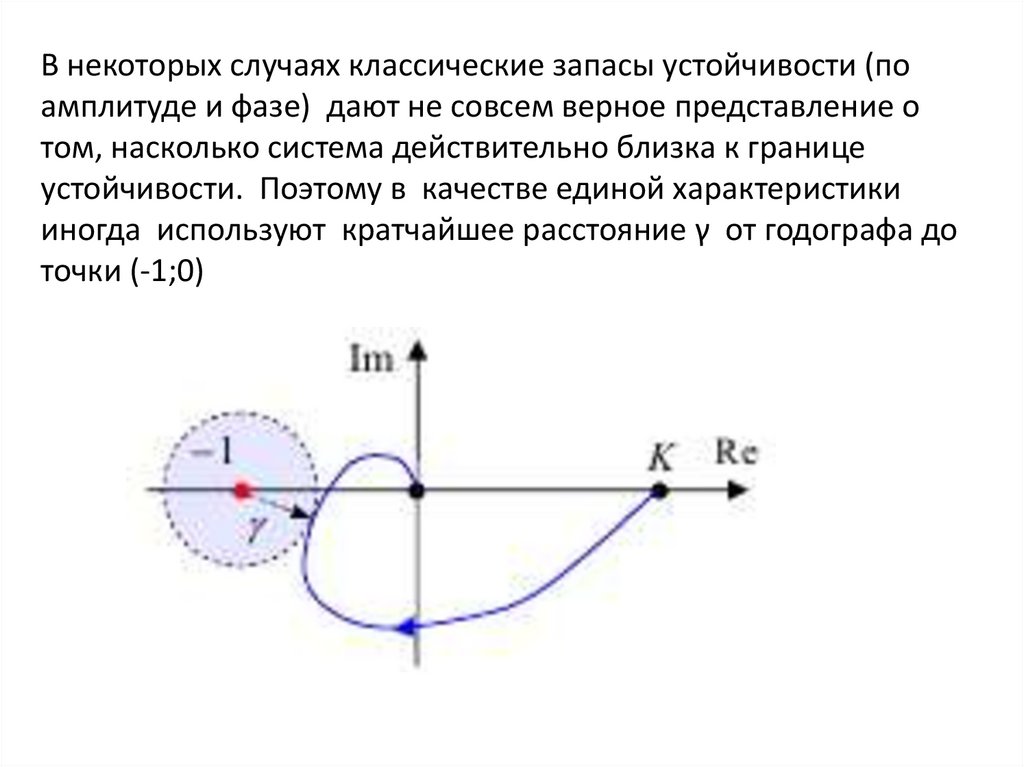
В некоторых случаях классические запасы устойчивости (поамплитуде и фазе) дают не совсем верное представление о
том, насколько система действительно близка к границе
устойчивости. Поэтому в качестве единой характеристики
иногда используют кратчайшее расстояние γ от годографа до
точки (-1;0)
21.
5.9. Область устойчивости в пространстве параметров АСРассмотрим простейший пример построения области устойчивости АС 3го порядка в плоскости ее параметров с применением критерия
Вышнеградского.
a 3 3 a 2 2 a1
p
p
p 1 0 .
A(p) = a3p3+ a2p2+ a1p+ a0 = 0
a0
a0
a0
Введем обозначения:
a3 3
p S 3 . p S 3 a0 / a 3 ,
a0
p 2 S 2 3 a02 / a32 ,
a2 2 a2 2 3 2 2
a2
p
S a0 / a3 A2 S 2 , A2
;
2
3
a0
a0
a a
3
0
a1
a1
a1
a0
A
.
p S3
A1S . 1 3
2
a 3 a 0 A2
a0
a0
a3
1 -область устойчивости АС;
1 2 -область неустойчивости АС.
S 3+ A 2 S2 + A 1 S + 1 = 0
A2A1 > 1 или A1 > 1/A2
Граница, разделяющая
плоскость на области
устойчивости и
неустойчивости АС в
плоскости ее параметров,
называется гиперболой
Вышнеградского.
2
A1













 Электроника
Электроника








