Похожие презентации:
Circuit analysis techniques (lecture 2)
1.
Circuit Analysis TechniquesOEk 1115 - Fundamentals of Electronics | Lecture 2
2.
OutlineBasic Circuit
Ohm’s Law
Resistance, Current, and Voltage
Power and Energy
Kirchhoff’s Voltage Law
Kirchhoff’s Current Law
3.
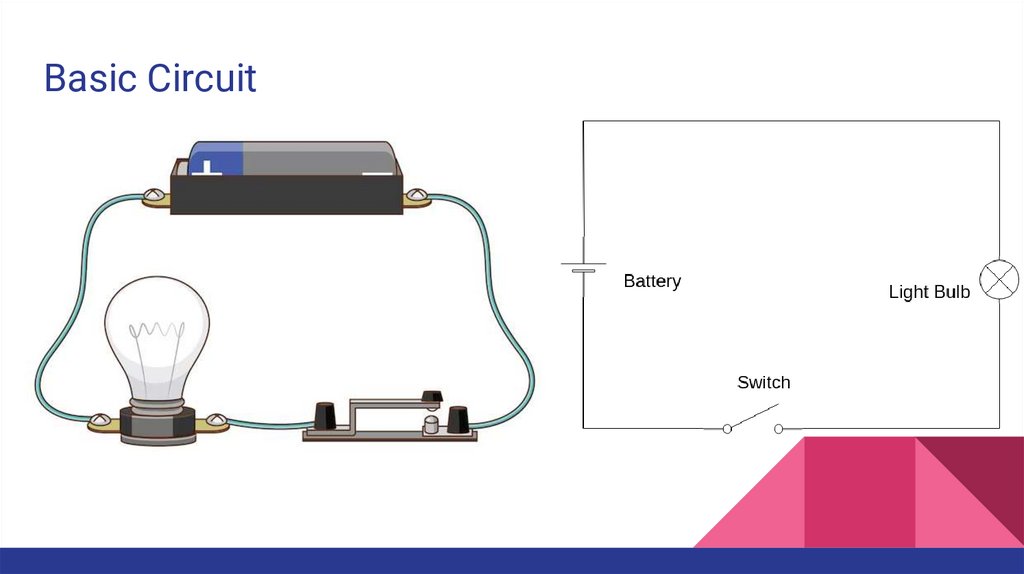
Basic Circuit4.
Ohm’s LawOhm's Law is a fundamental principle in electronics that
relates voltage, current, and resistance in a circuit.
Named after the German physicist Georg Simon Ohm.
5.
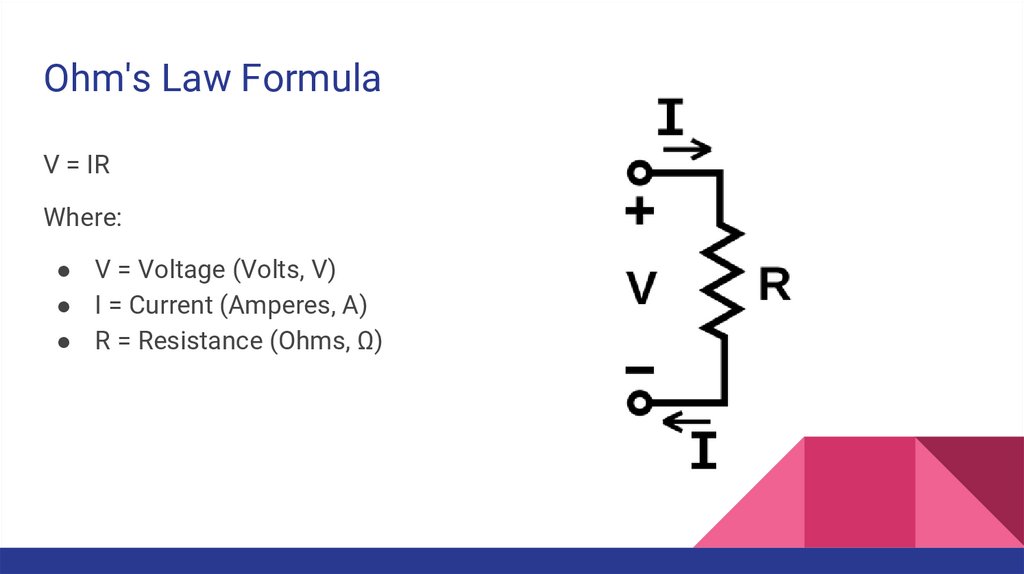
Ohm's Law FormulaV = IR
Where:
● V = Voltage (Volts, V)
● I = Current (Amperes, A)
● R = Resistance (Ohms, Ω)
6.
Ohm's Law FormulaVoltage (V) is the electrical pressure that drives current (I) through a circuit.
Current (I) is the flow of electrons and is influenced by the resistance (R) in the
circuit.
7.
Ohm's Law ExampleSuppose we have a resistor with a resistance of 100 Ω and a current of 0.5 A
passing through it.
What is the voltage across the resistor?
8.
Ohm's Law CalculationUsing Ohm's Law: V = IR
V = (0.5 A) * (100 Ω) = 50 V
So, the voltage across the resistor is 50 volts.
9.
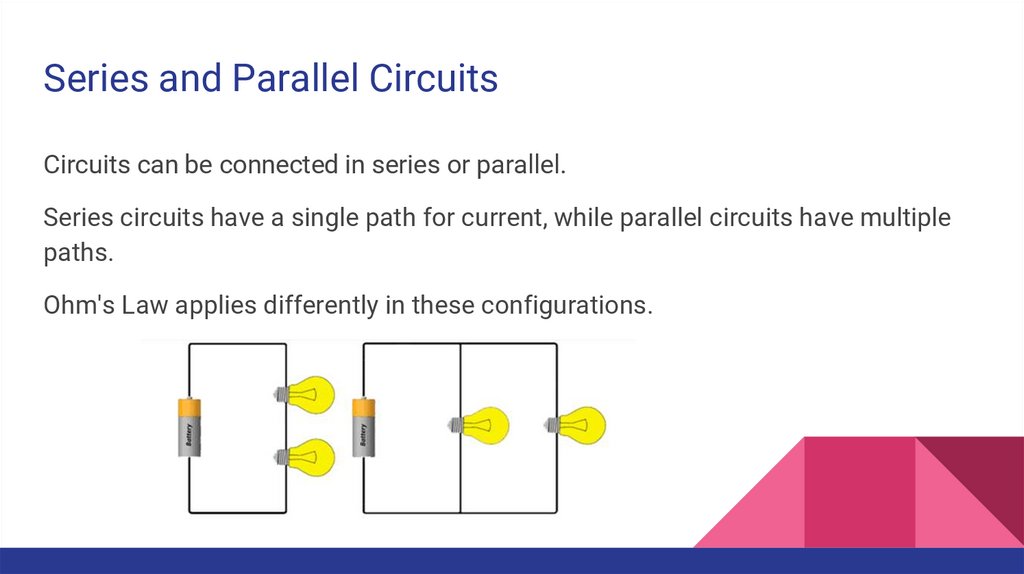
Series and Parallel CircuitsCircuits can be connected in series or parallel.
Series circuits have a single path for current, while parallel circuits have multiple
paths.
Ohm's Law applies differently in these configurations.
10.
Series and Parallel CircuitsIn series circuits, total resistance is the sum of individual resistances
● R_total = R1 + R2 + ...
In parallel circuits, total resistance is calculated differently
● 1/R_total = 1/R1 + 1/R2 + ...
11.
Practical ApplicationUnderstanding Ohm's Law is crucial for designing and troubleshooting circuits.
Engineers and technicians use it daily in fields like electronics,
telecommunications, and electrical engineering.
12.
Practical ApplicationResistor Sizing in LED Circuits:
● When designing an LED circuit, you need to determine the appropriate currentlimiting resistor to prevent the LED from burning out. Ohm's Law helps
calculate the resistor value based on the supply voltage and desired LED
current.
13.
Practical ApplicationBattery Life Estimation:
● Ohm's Law is used to estimate the battery life of portable devices. By
analyzing the current drawn by the device and the battery's capacity, you can
calculate how long the battery will last before needing a recharge or
replacement.
14.
Review Question1. In Ohm's Law (V = IR), what do V, I, and R represent?
2. Why is it important to use a current-limiting resistor when connecting an LED
to a power source?
3. Explain why it's important to consider voltage drop in electrical wiring
installations.
15.
Energy and PowerWhen there is current through a resistance, electrical energy is converted to heat
or other form of energy, such as light.
A common example of this is a light bulb that becomes too hot to touch. The
current through the filament that produces light also produces unwanted heat
because the filament has resistance.
Electrical components must be able to dissipate a certain amount of energy in a
given period of time.
16.
Energy and PowerEnergy is the ability to do work, and power is the rate at which energy is used.
In other words, power, P, is a certain amount of energy, W, used in a certain length
of time (t), expressed as follows: P = W / t
The joule is the SI unit for energy.
One watt is the amount of power when one joule of energy is used in one second.
17.
Energy and PowerExample. An amount of energy equal to 100 J is used in 5 s. What is the power in
watts?
18.
Energy and PowerExample. An amount of energy equal to 100 J is used in 5 s. What is the power in
watts?
Solution:
19.
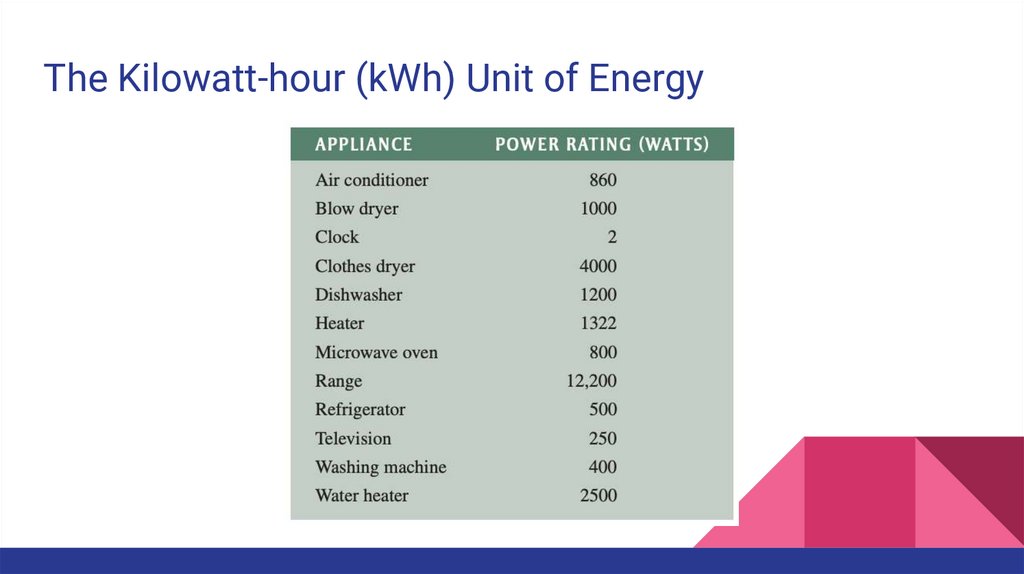
The Kilowatt-hour (kWh) Unit of EnergyThe joule has been defined as the unit of energy. However, there is another way to
express energy. Since power is expressed in watts and time can be expressed in
hours, a unit of energy called the kilowatt-hour (kWh) can be used.
When you pay your electric bill, you are charged on the basis of the amount of
energy you use. Because power companies deal in huge amounts of energy, the
most practical unit is the kilowatt-hour. You use a kilowatt-hour of energy when
you use the equivalent of 1000 W of power for 1 h. For example, a 100 W light bulb
burning for 10 h uses 1 kWh of energy.
W = Pt = (100 W)(10 h) = 1000 Wh = 1 kWh
20.
The Kilowatt-hour (kWh) Unit of EnergyExample. Determine the number of kilowatt-hours (kWh) for each of the following
energy consumptions:
(a) 1400 W for 1 hr
(b) 2500 W for 2 h
(c) 100,000 W for 5 h
21.
The Kilowatt-hour (kWh) Unit of EnergySolution:
22.
The Kilowatt-hour (kWh) Unit of Energy23.
Power in an Electric CircuitWhen there is current through a resistance, the collisions of the electrons as they
move through the resistance give off heat, resulting in a conversion of electrical
energy to thermal energy.
P = I^2 x R
24.
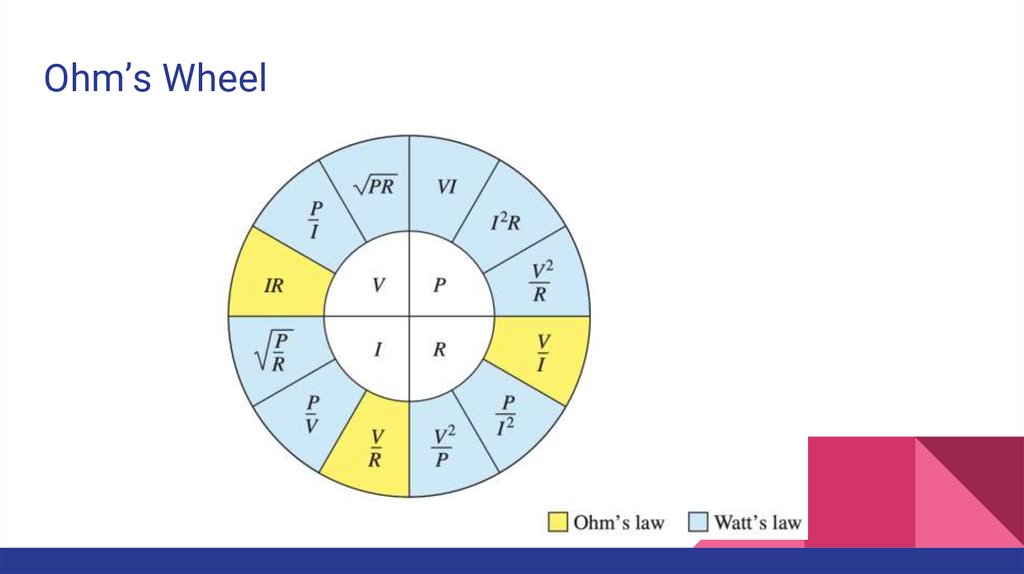
Ohm’s Wheel25.
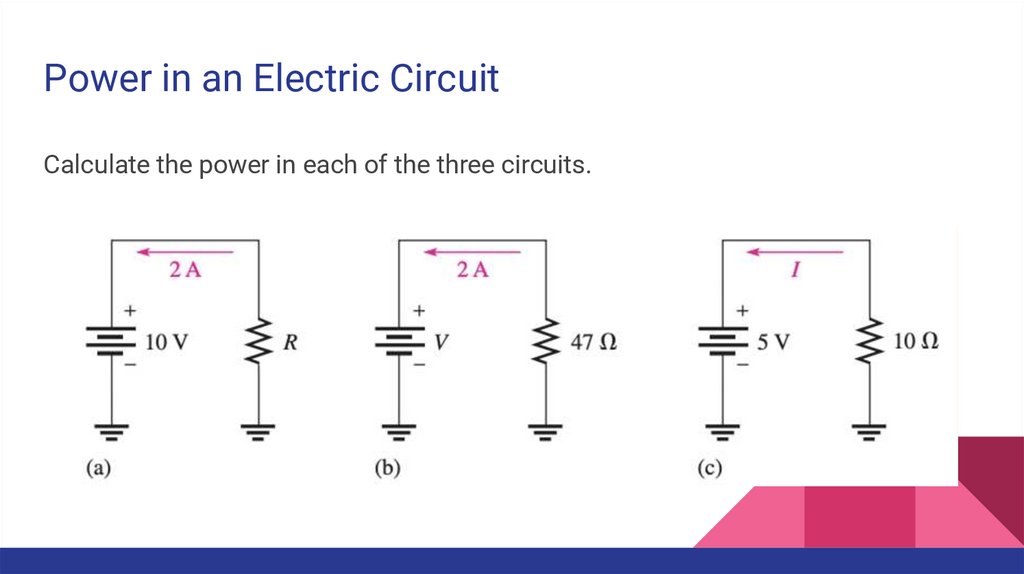
Power in an Electric CircuitCalculate the power in each of the three circuits.
26.
Power in an Electric CircuitA solar yard light has a solar collector that can provide 1.0 W of power for
charging the 3.0 V batteries. What is the maximum charging current the solar
collector could supply to fully discharged 3.0 V batteries?
27.
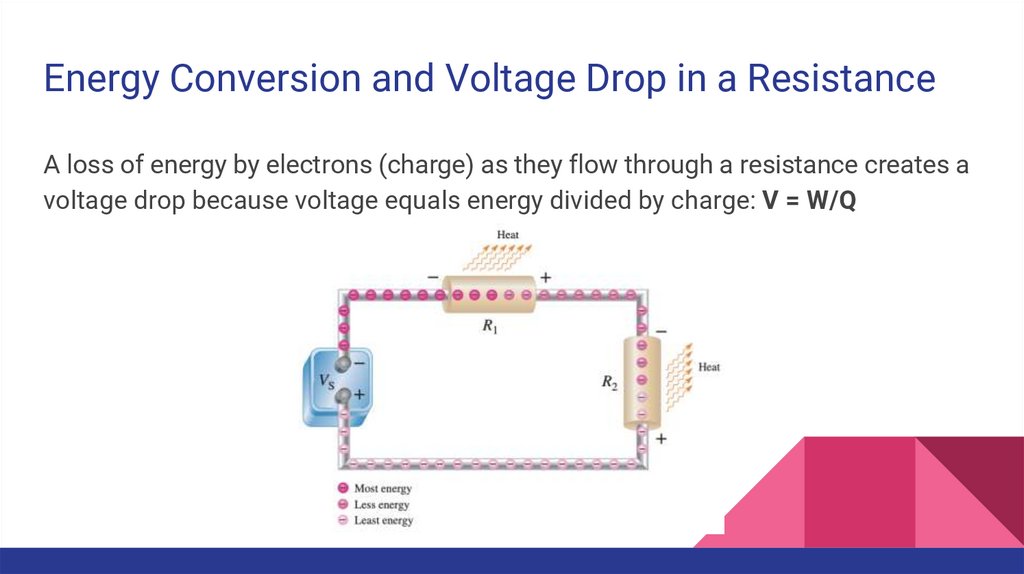
Energy Conversion and Voltage Drop in a ResistanceA loss of energy by electrons (charge) as they flow through a resistance creates a
voltage drop because voltage equals energy divided by charge: V = W/Q
28.
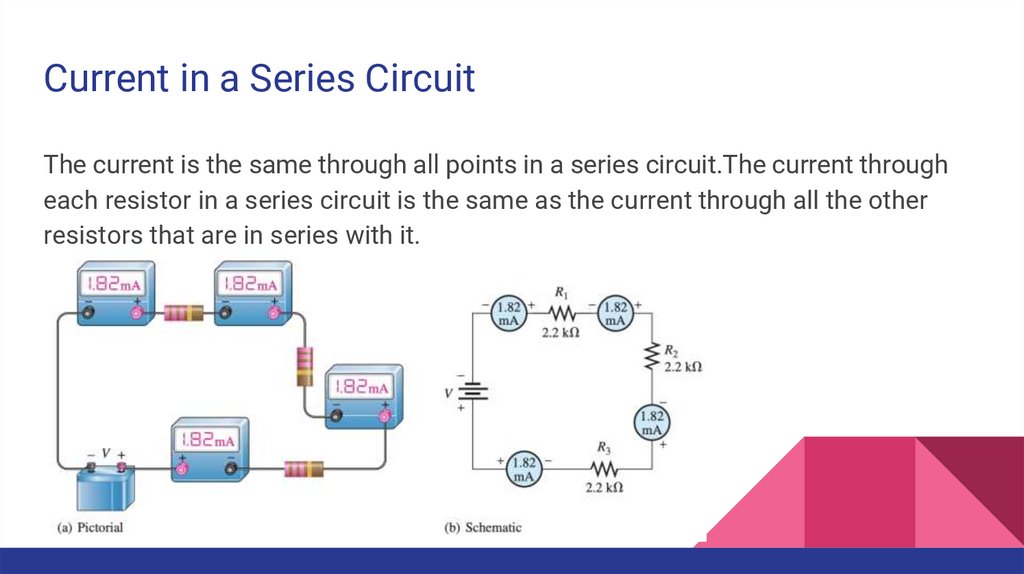
Current in a Series CircuitThe current is the same through all points in a series circuit.The current through
each resistor in a series circuit is the same as the current through all the other
resistors that are in series with it.
29.
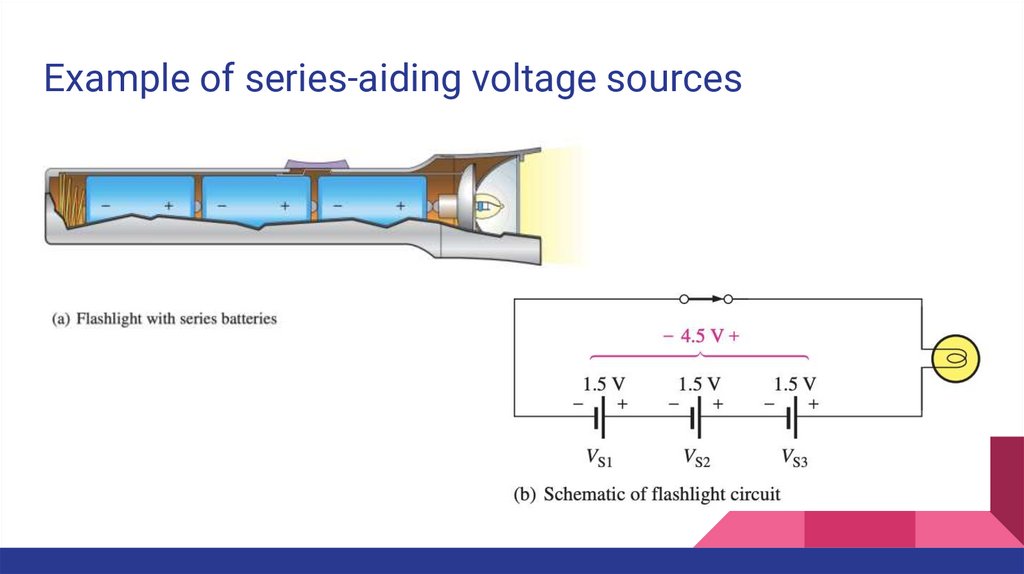
Voltage Sources in SeriesRecall that a voltage source is an energy source that provides a constant voltage
to a load.
Batteries and power supplies are practical examples of dc voltage sources.
When two or more voltage sources are in series, the total voltage is equal to the
algebraic sum of the individual source voltages.
30.
Example of series-aiding voltage sources31.
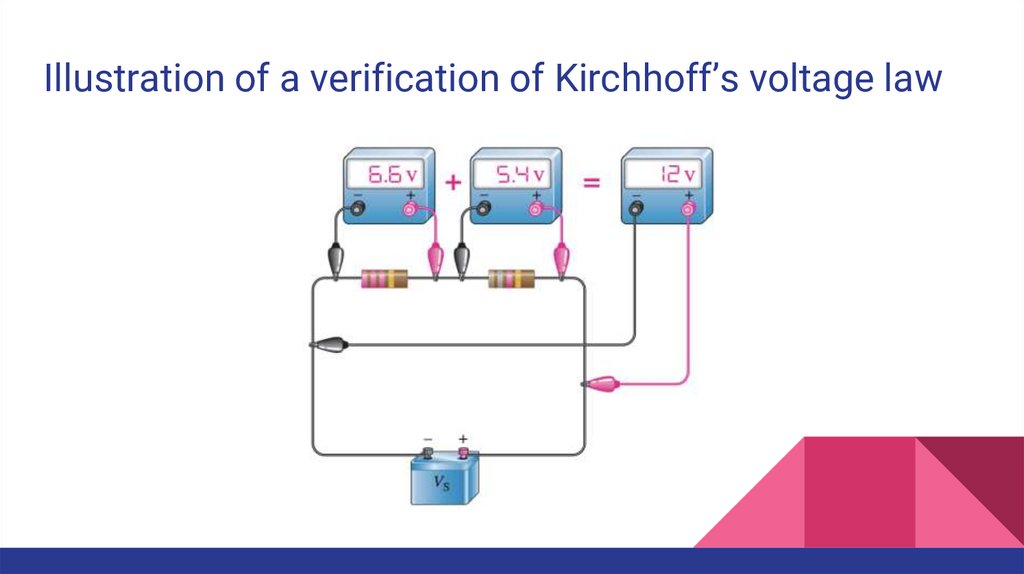
Kirchhoff’s Voltage LawKirchhoff’s voltage law is a fundamental circuit law
that states that the algebraic sum of all the voltages
around a single closed path is zero or, in other words,
the sum of the voltage drops equals the total source
voltage.
The sum of all the voltage drops around a single
closed path in a circuit is equal to the total source
voltage in that closed path.
32.
Illustration of a verification of Kirchhoff’s voltage law33.
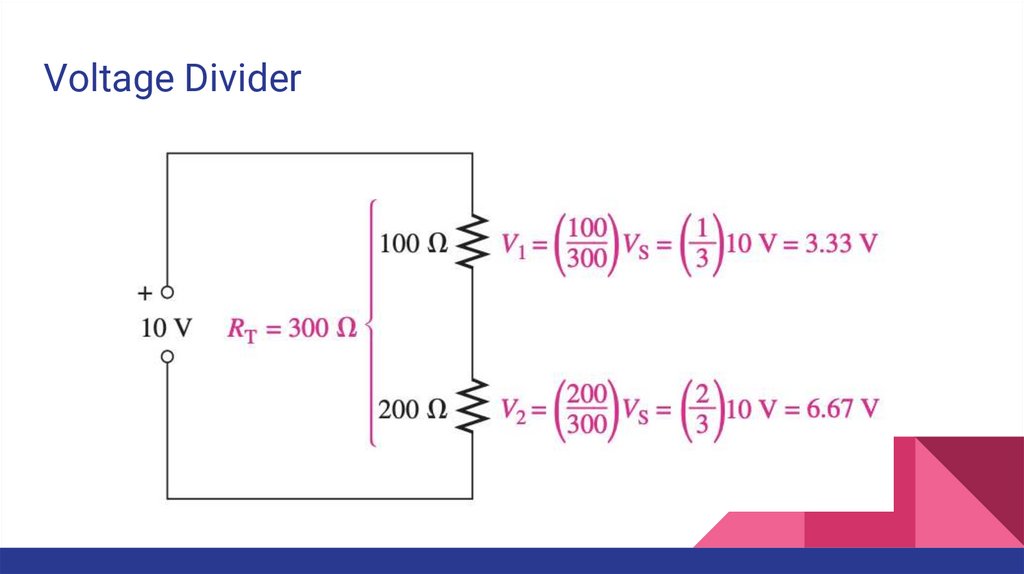
Voltage DividerA circuit consisting of a series string of resistors connected to a voltage source
acts as a voltage divider.
The total voltage drop around a single closed path divides among the series
resistors in amounts directly proportional to the resistance values.
34.
Voltage Divider35.
Voltage Divider36.
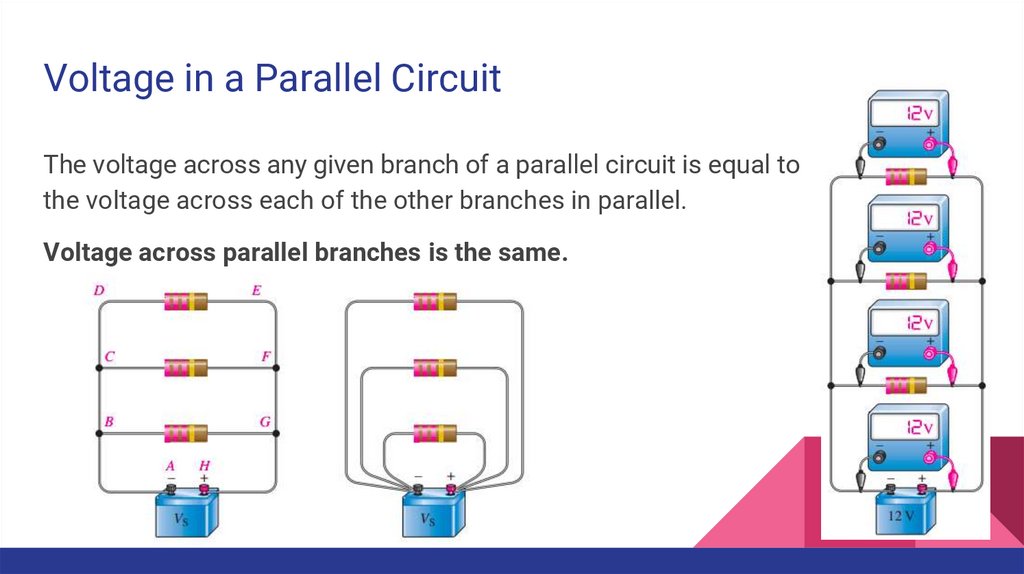
Voltage in a Parallel CircuitThe voltage across any given branch of a parallel circuit is equal to
the voltage across each of the other branches in parallel.
Voltage across parallel branches is the same.
37.
Kirchhoff’s Current LawKirchhoff’s voltage law deals with voltages in a single closed path.
Kirchhoff’s current law applies to currents in multiple paths.
The sum of the currents into a node (total current in) is equal to the sum of the
currents out of that node (total current out).
38.
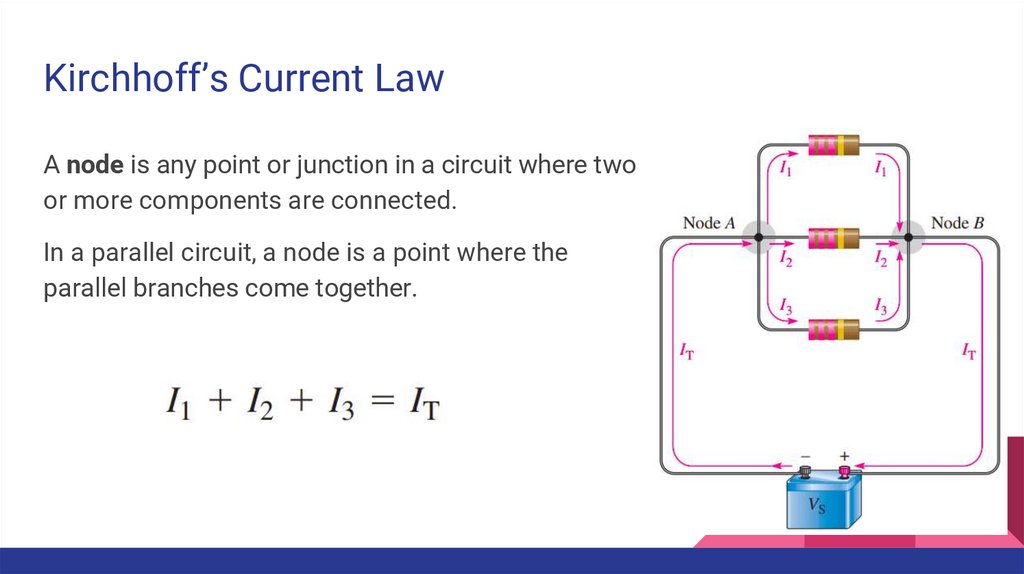
Kirchhoff’s Current LawA node is any point or junction in a circuit where two
or more components are connected.
In a parallel circuit, a node is a point where the
parallel branches come together.
39.
Kirchhoff’s Current LawBy Kirchhoff’s current law, the sum of
the currents into a node must equal the
sum of the currents out of that node.
The algebraic sum of all of the currents
entering and leaving a node is equal to
zero.
40.
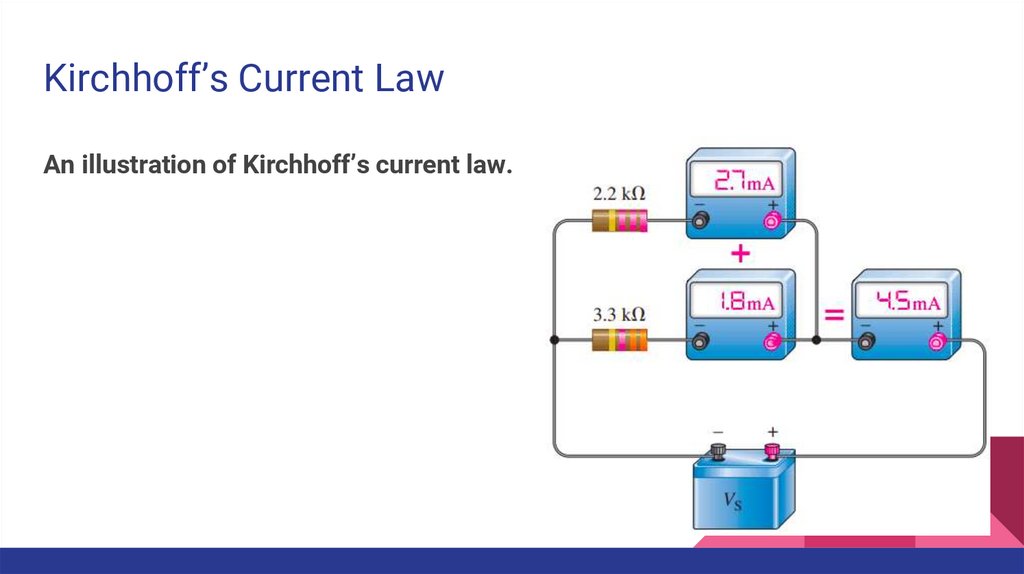
Kirchhoff’s Current LawAn illustration of Kirchhoff’s current law.
41.
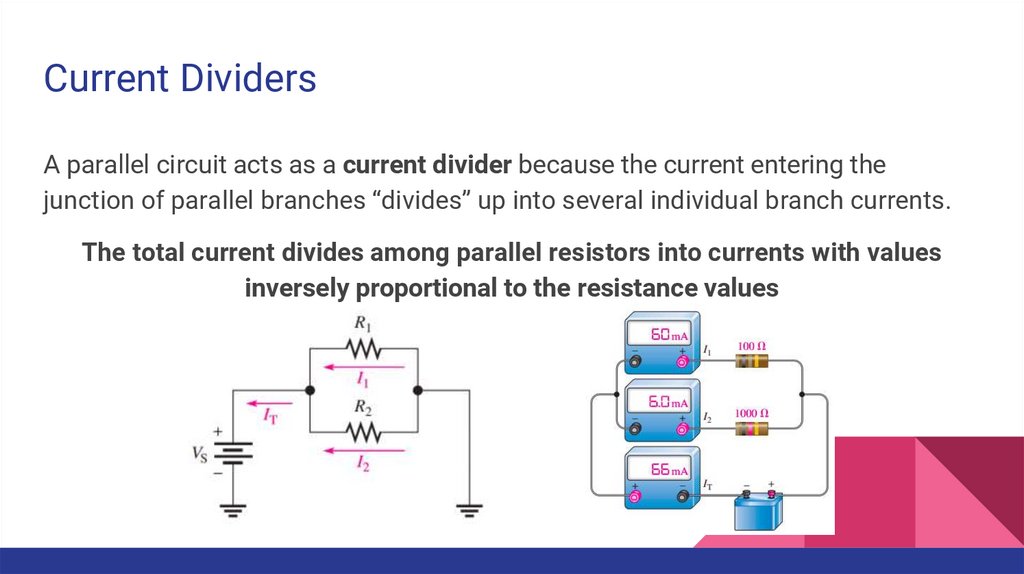
Current DividersA parallel circuit acts as a current divider because the current entering the
junction of parallel branches “divides” up into several individual branch currents.
The total current divides among parallel resistors into currents with values
inversely proportional to the resistance values
42.
Current DividersThe current (Ix) through any branch equals the total parallel resistance (RT)
divided by the resistance (Rx) of that branch, and then multiplied by the total
current (IT) into the junction of parallel branches.
43.
Q&AAny Questions?




























 Физика
Физика








