Системы линейных уравнений

1. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

ЛЕКЦИЯ 2
1

2. Система n линейных уравнений с n переменными имеет вид

а11х1 а12 х2 ... а1n хn b1
а21х1 а22 х2 ... а2 n хn b2
...........................................
а х а х ... а х b
nn n
n
n2 2
n1 1
(1.1)
где x1, x2, …, xn переменные,
aij числовые коэффициенты
ЛЕКЦИЯ 2
2

3.

Пусть дана система линейных
уравнений
а11х1 а12 х2 ... а1n хn b1
а х а х ... а х b
21 1
22 2
2n n
2
...........................................
аm1 х1 аm 2 х2 ... аmn хn bm
(1.2)
Краткая запись:
а x
n
j 1
ij
j
bi , i 1,2,...m,
ЛЕКЦИЯ 2
j 1,2,...n
3

4.

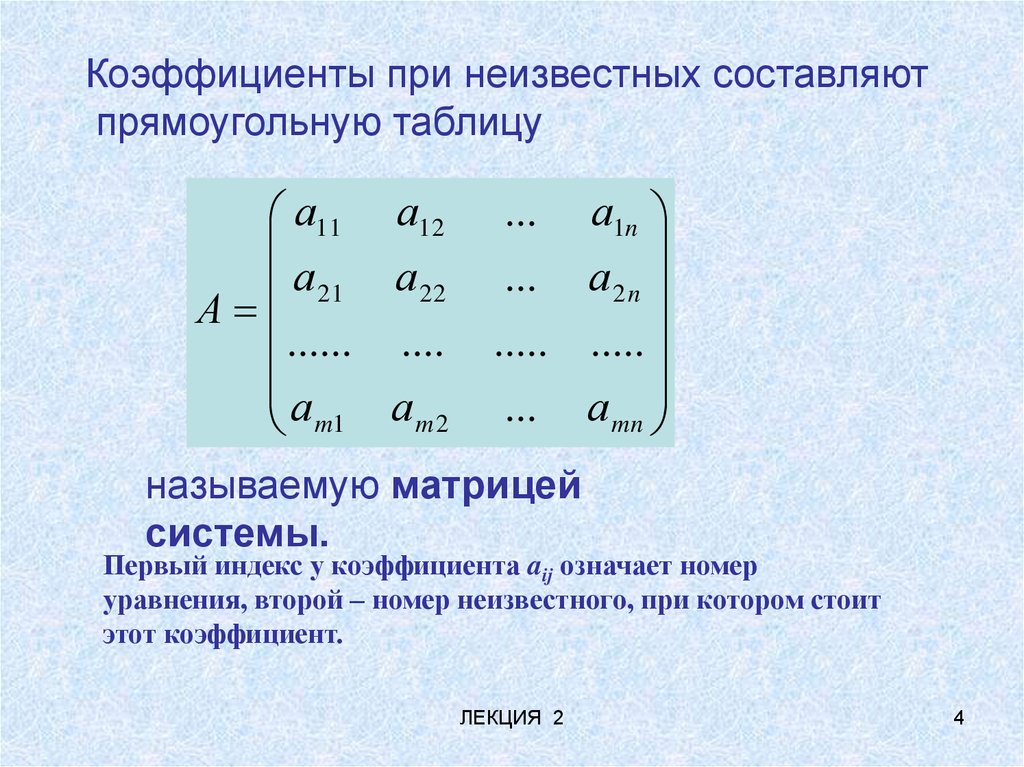
Коэффициенты при неизвестных составляют
прямоугольную таблицу
а11 а12
а 21 а 22
А
...... ....
а
m1 а m 2
а1n
... а 2 n
..... .....
... а mn
...
называемую матрицей
системы.
Первый индекс у коэффициента aij означает номер
уравнения, второй – номер неизвестного, при котором стоит
этот коэффициент.
ЛЕКЦИЯ 2
4

5.

Коэффициенты b1 ,b2 , …, bm называются
свободными членами уравнений системы.
Если свободные члены равны нулю, то система
называется однородной,
а11 х1 а12 х 2 ... а1n х n 0
а х а х ... а х 0
21 1
22 2
2n n
...........................................
а m1 х1 а m 2 х 2 ... а mn х n 0
в противном случае – неоднородной.
ЛЕКЦИЯ 2
5

6.

Матрицу
а11
а 21
В
...
a
m1
а12
... а1n
a 22
... a 2 n
...
...
am2
...
... a mn
b1
b2
...
bm
называют расширенной матрицей системы (1.2)
ЛЕКЦИЯ 2
6

7.

Решение системы (1.1), (1,2)- это упорядоченный
набор (х1,х2, ..., хп) из п чисел, при подстановке
которых в уравнения системы вместо
соответствующих неизвестных каждое уравнение
системы превращается в тождество.
Система, не имеющая ни одного решения, называется
несовместной или противоречивой. Система, имеющая
хотя бы одно решение, называется совместной.
Совместные системы подразделяют на определенные, обладающие
единственным решением, и неопределенные, обладающие
множеством решений.
Однородная система всегда совместна, так как имеет, по крайней
мере, нулевое решение
ЛЕКЦИЯ 2
7

8.

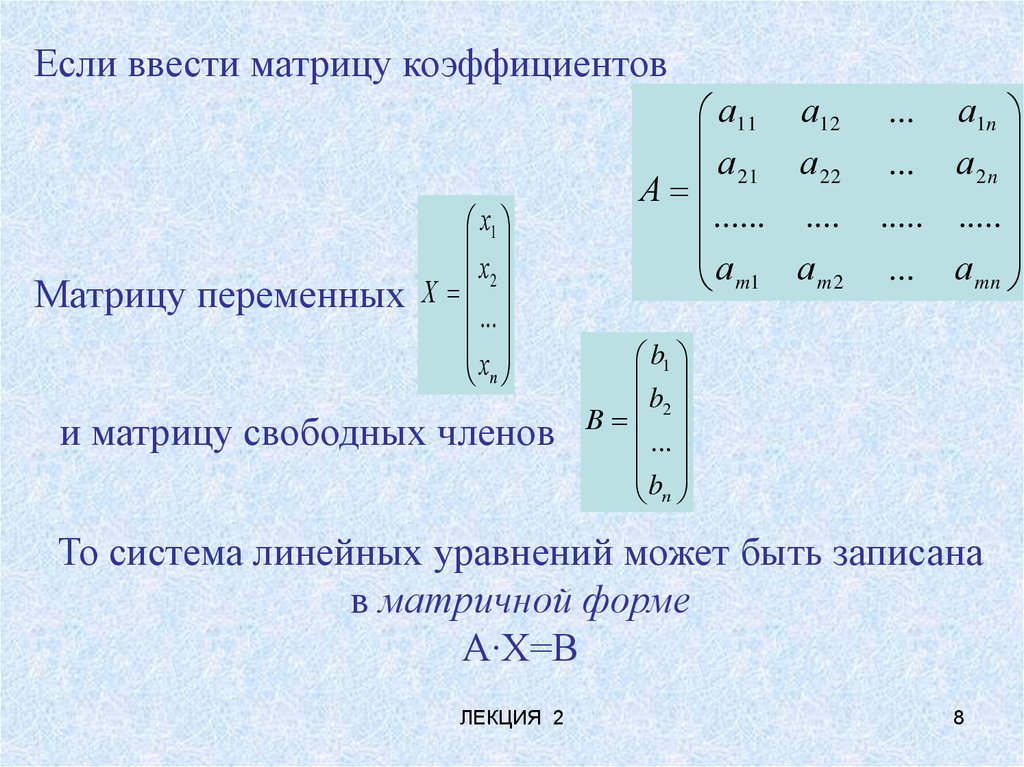
Если ввести матрицу коэффициентов
Матрицу переменных
х1
х2
Х
...
хп
и матрицу свободных членов
а11 а12
а 21 а 22
А
...... ....
а
m1 а m 2
а1n
... а 2 n
..... .....
... а mn
...
b1
b2
В
...
bп
То система линейных уравнений может быть записана
в матричной форме
А∙Х=В
ЛЕКЦИЯ 2
8

9.

Методы решения систем линейных уравнений
1.Метод Гаусса.
Метод заключается в последовательном
исключении переменных путем некоторых
элементарных преобразований, в результате чего
система приводится к ступенчатому виду с
нулями ниже главной диагонали. Переменные
находятся, начиная с последних по номеру
переменных.
ЛЕКЦИЯ 2
9

10.

Методы решения систем линейных уравнений
2. Метод Гаусса-Жордана.
Представляет собой продолжение метода
Гаусса, заключающееся в том, что нули
получают также выше главной диагонали.
Элементы на главной диагонали приводят к
единицам, в результате чего из полученной
матрицы выписывается сразу решение
системы.
ЛЕКЦИЯ 2
10

11.

Методы решения систем линейных уравнений
3. Метод Крамера.
Переменные могут быть найдены по формулам Крамера
где Δ - определитель матрицы коэффициентов перед
переменными,
Δј - определитель матрицы, получаемой из матрицы А
заменой ј-го столбца на столбец свободных членов.
ЛЕКЦИЯ 2
11

12.

Методы решения систем линейных уравнений
4. Метод обратной матрицы.
Из матричного уравнения АХ=В следует, что Х=А-1В.
Найдя обратную матрицу и умножив ее на матрицу
свободных членов, получаем матрицу переменных.
ЛЕКЦИЯ 2
12

13. Теорема. (теорема Кронекера - Капелли)

Для того чтобы система линейных уравнений (1.2) была
совместной, необходимо и достаточно, чтобы ранг её
матрицы был равен рангу её расширенной матрицы.
Теорема.
Если система линейных уравнений (1.2) совместна, то:
1) для того, чтобы эта система была определенной,
необходимо и достаточно. чтобы ранг матрицы системы
был равен числу её переменных;
2) для того, чтобы эта система была неопределенной,
необходимо и достаточно, чтобы ранг её матрицы был
меньше числа её переменных.
ЛЕКЦИЯ 2
13

14. Пример. Решить систему уравнений

x x x 10,
1
2
3
2 x1 3 x2 x3 22,
4
x
5
x
3
x
42.
2
3
1
ЛЕКЦИЯ 2
14

15. Метод Гаусса

ЛЕКЦИЯ 2
15

16. Теорема. Элементарные преобразования расширенной матрицы данной системы, выполненные лишь над её строками, превращают эту

матрицу в расширенную матрицу
другой системы, равносильной данной.
x1, x2 – базисные переменные
x3 – свободные переменные
x3 = 2,
x2 = 4,
системы.
x1= 4 –частное решение
ЛЕКЦИЯ 2
16

17. Пример. Решить систему

.
x x x 10,
1
2
3
2 x1 3 x2 x3 22,
5
x
4
x
3
x
39.
2
3
1
ЛЕКЦИЯ 2
17

18. Метод Крамера

ЛЕКЦИЯ 2
18

19. Пример. Решить систему

3 x 2 x x 0,
1
2
3
2 x1 x2 5 x3 0,
7
x
9
x
0.
3
1
ЛЕКЦИЯ 2
19

20. Теорема

Чтобы система однородных уравнений имела
ненулевое решение, необходимо и достаточно,
чтобы ранг её матрицы был меньше числа
переменных.
Следствие. Если матрица системы однородных
уравнений квадратная, то для того, чтобы
система имела ненулевое решение, необходимо и
достаточно, чтобы определитель её матрицы был
равен нулю.
ЛЕКЦИЯ 2
20

21. Найдем ранг матрицы системы

ЛЕКЦИЯ 2
21

22. Составим систему однородных уравнений эквивалентную данной

ЛЕКЦИЯ 2
22