Лек4

1. Лекция 4

2.

Непараметрические распределения

3.

Цель первичной обработки экспериментальных
наблюдений - выбор закона распределения, наиболее
хорошо описывающего случайную величину,
выборку которой наблюдают.
Насколько хорошо наблюдаемая выборка
описывается теоретическим законом, проверяют с
помощью различных критериев согласия.

4.

Цель проверки гипотезы о согласии опытного
распределения с теоретическим – стремление
удостовериться: данная модель теоретического
закона не противоречит наблюдаемым данным,
и использование ее не приведет к существенным
ошибкам при вероятностных расчетах.
Некорректное использование критериев согласия
может приводить к необоснованному принятию
(чаще всего) или необоснованному отклонению
проверяемой гипотезы.

5.

Проверка статистических гипотез о согласии
эмпирических данных с теоретическим законом
распределения обычно осуществляется с
применением критериев типа χ2 или
непараметрических критериев.
Рассмотрим применение непараметрических
критериев согласия, в частности, применение
критериев Колмогорова, Смирнова-Крамера-фон
Мизеса, Андерсона-Дарлинга, Купера, Ватсона,
Жанга.

6.

Практика применения такого рода критериев в
приложениях богата большим количееством
примеров некорректного использования.
Наиболее распространенные ошибки применения
связаны с использованием классических результатов
при проверке простых гипотез, для ситуаций,
соответствующих проверке сложных гипотез.

7.

При проверке согласия различают простые и
сложные гипотезы.
Простая проверяемая гипотеза имеет вид
H0: F(x) = F(x, θ), где F(x, θ)– функция
распределения вероятностей, с которой проверяют
согласие наблюдаемой выборки, а θ – известное
значение параметра (скалярного или векторного).
Сложная проверяемая гипотеза имеет вид
H0: F ( x) F ( x, ),
где Θ – область определения параметра θ.

8.

Если процесс вычисления оценки ̂ скалярного или
векторного параметра закона не опирается на ту же
самую выборку, по которой проверяют гипотезу о
согласии, то алгоритм применения критерия
согласия при проверке сложной гипотезы не
отличается от проверки простой гипотезы.

9.

Проблемы возникают, если при проверке сложной
гипотезы оценку ̂ параметра распределения
вычисляют по той же самой выборке, по которой
проверяют согласие.
Будем предполагать: оценка параметра ̂
вычисляется по той же выборке.
Очевидно: на практике при обработке результатов
измерений с проблемой проверки сложных гипотез
чаще всего сталкиваются именно в такой ситуации,
поскольку сначала оценивают по выборке
параметры модели, чтобы лучше подогнать ее к
наблюдаемым данным, а потом проверяют
адекватность полученной модели.

10.

Схема проверки гипотезы:
В соответствии с применяемым критерием согласия
вычисляют значение S* статистики критерия S как
некоторой функции от выборки и теоретического
закона распределения с плотностью F(x, θ0), [или
F(x, ̂ )при сложной гипотезе]. Для используемых на
практике критериев асимптотические (предельные)
распределения G(S|H0) соответствующих статистик
при условии истинности гипотезы H0 обычно
известны.
Обычно, для ситуаций проверки простых и сложных
гипотез эти распределения различаются.

11.

В ситуации проверки простых гипотез предельные
распределения статистик классических
непараметрических критериев согласия известны и
не зависят от вида наблюдаемого закона
распределения и, в частности, от его параметров.
Говорят: эти критерии являются «свободными от
распределения». Это достоинство предопределило
широкое использование данных критериев в
различных приложениях.

12.

Далее в принятой практике статистического анализа
обычно полученное значение статистики S*
сравнивают с критическим значением Sα при
заданном уровне значимости α.
Нулевую гипотезу отвергают, если S* > Sα

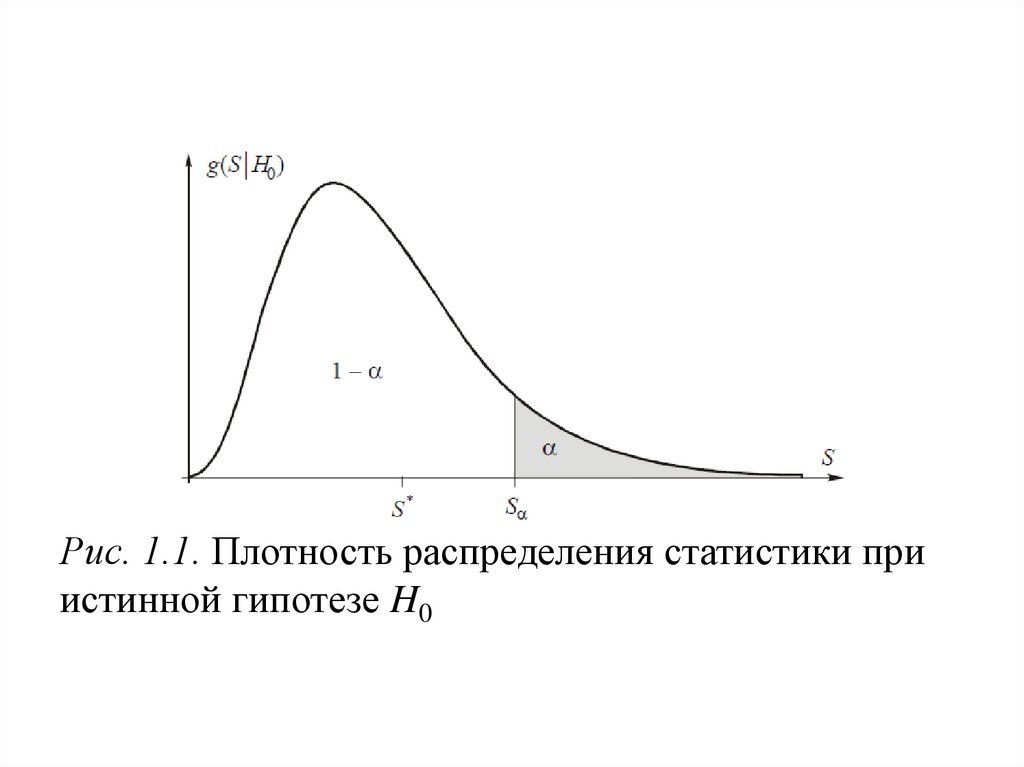
13.

Рис. 1.1. Плотность распределения статистики при
истинной гипотезе H0

14.

Критическое значение Sα, определяемое в
случае одномерной статистики из уравнения
где g(s|H0 ) − условная плотность
распределения статистики,
обычно берут из соответствующей
статистической таблицы или вычисляют.

15.

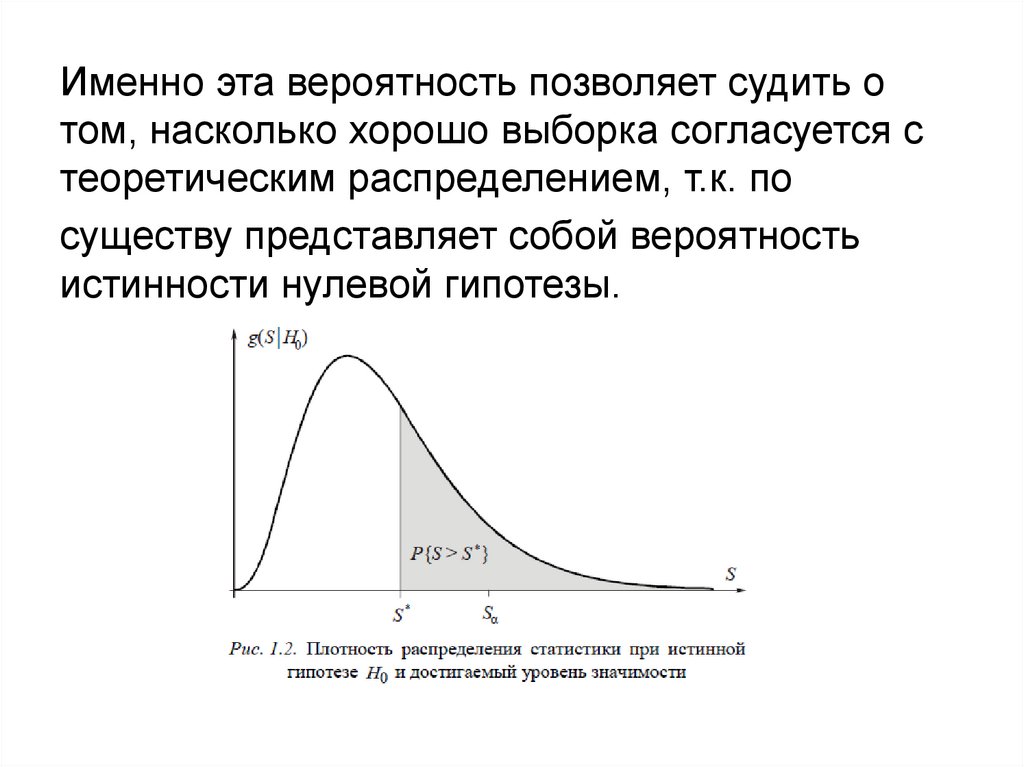
Больше информации о степени согласия можно
почерпнуть из «достигаемого уровня
значимости»: величины вероятности
возможного превышения полученного значения
статистики при истинности нулевой гипотезы

16.

Именно эта вероятность позволяет судить о
том, насколько хорошо выборка согласуется с
теоретическим распределением, т.к. по
существу представляет собой вероятность
истинности нулевой гипотезы.

17.

Гипотезу о согласии не отвергают, если
P{S>S*} > α.
Задачи оценивания параметров и проверки
гипотез опираются на выборки независимых
случайных величин.
Случайность самой выборки предопределяет:
возможны и ошибки в результатах
статистических выводов.

18.

С результатами проверки гипотез связывают
ошибки двух видов: ошибка первого рода
состоит в том, что
отклоняют гипотезу H0, когда она верна; ошибка
второго рода состоит в том, что принимают
гипотезу H0, в то время как справедлива
конкурирующая гипотеза H1.

19.

Уровень значимости α задает вероятность
ошибки первого рода. Обычно в критериях
согласия не рассматривают конкретную
конкурирующую гипотезу. И тогда можно
считать, что конкурирующая гипотеза имеет вид
H1:
F(x) ≠ F(x, θ0),
Если же гипотеза H1 задана и имеет, например,
вид H1: F(x) = F(x, θ1), то задание величины α
для используемого критерия проверки гипотез
определяет и вероятность ошибки второго рода
β

20.

На рис. 1.3 g(s|H0) отображает плотность
распределения статистики S при истинности
гипотезы H0, а g(s|H1) – плотность
распределения при справедливости H1 .
Рис. 1.3. Плотности распределения статистик при
справедливости гипотез H0 и H1

21.

Мощность критерия представляет собой
величину 1- β.
Очевидно: чем выше мощность используемого
критерия при заданном значении α, тем лучше
он различает гипотезы H0 и H1.
Особенно важно, чтобы этот критерий хорошо
различал близкие конкурирующие гипотезы.
Графически требование максимальной
мощности критерия означает: на рис. 1.3
плотности g(s|H0) и g(s|H1) должны быть
максимально «раздвинуты».

22.

23.

Стандартное распределение — нормальное
распределение (распределение Гаусса) с
параметрами: a = 0, σ2 =1.
Плотность распределения f(x) определяется
формулой

24.

график функции f(x) и uγ — симметричная квантиль
стандартного распределения порядка γ .
Рис.1. График плотности вероятности стандартного
распределения

25.

Распределение Хи-квадрат с k степенями свободы
— распределение случайной величины χ2(k), которая
равна сумме квадратов k независимых случайных
величин Ui , i=1,2,...,k, каждая из которых
распределена стандартно:

26.

Плотность распределения f χ2 (x) определяется:
где
— гамма-функция;
z — любое комплексное число, кроме 0, -1, -2, ... .

27.

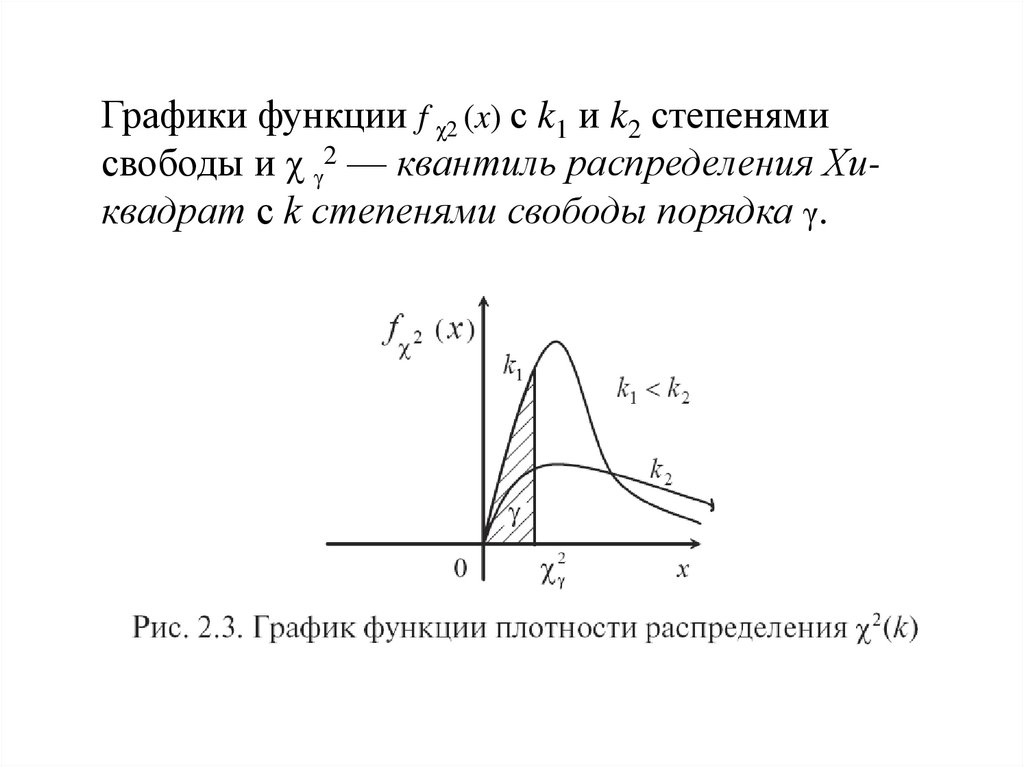
Графики функции f χ2 (x) с k1 и k2 степенями
свободы и χ γ2 — квантиль распределения Хиквадрат с k степенями свободы порядка γ.

28.

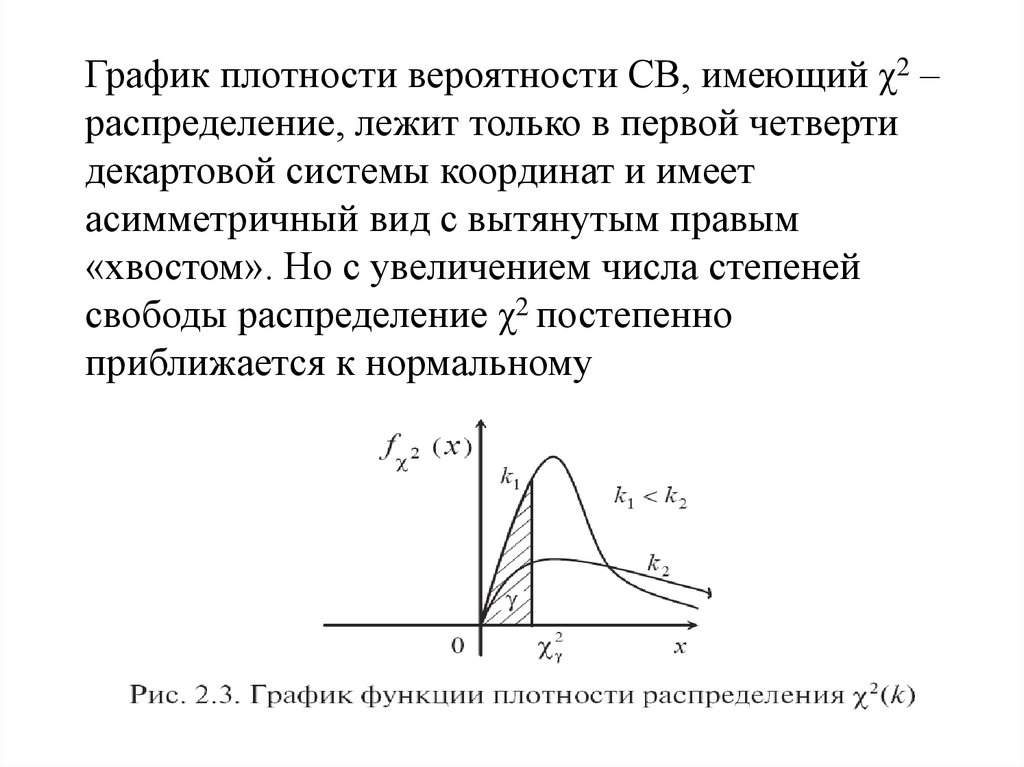
График плотности вероятности СВ, имеющий χ2 –
распределение, лежит только в первой четверти
декартовой системы координат и имеет
асимметричный вид с вытянутым правым
«хвостом». Но с увеличением числа степеней
свободы распределение χ2 постепенно
приближается к нормальному

29.

Распределение χ2 применяется для
нахождения интервальных оценок и проверки
статистических гипотез.
При этом используется таблица критических
точек χ2 – распределения.

30.

Распределение Стьюдента с k степенями свободы
— распределение случайной величины T(k), равной
отношению двух независимых случайных величин:
где U — распределена стандартно.

31.

Плотность распределения fT(x) определяется:

32.

Графики функции fT(x) с k1 и k2 степенями
свободы и tγ — симметричная квантиль
распределения Стьюдента с k степенями
свободы порядка γ.
Все квантили находятся либо по таблицам, либо с помощью
компьютерных вычислений.

33.

распределение Стьюдента определяется только
одним параметром k – числом степеней свободы.
График функции плотности вероятности СВ,
имеющей распределение Стьюдента, является
симметричной кривой

34.

Распределение Стьюдента применяется для
нахождения интервальных оценок, а также при
проверке статистических гипотез.
При этом активно используется таблица
критических точек распределения Стьюдента.

35.

Доверительные интервалы для параметров
нормально распределенной генеральной
совокупности
Доверительный интервал для математического
ожидания случайной величины при известной
дисперсии

36.

Построим доверительный интервал для
математического ожидания случайной величины с
нормальным распределением при известной
дисперсии σ2 и доверительной вероятности γ.
1. Пусть {x1, x2, …, xn } — выборка из нормально
распределенной генеральной совокупности.
2. В качестве оценки математического ожидания а
возьмем выборочное среднее:

37.

Выборочное среднее x в данном случае имеет
нормальное распределение с числовыми
характеристиками:

38.

3. Рассмотрим вспомогательную случайную
величину
Она подобрана так, чтобы ее распределение было
стандартным независимо от параметра а:

39.

Действительно, т.к.
и
то
- функция от случайной величины x,

40.

Поскольку
Следовательно
Т.о., действительно, вспомогательная случайная
величина Y распределена стандартно.

41.

4. По центральной предельной теореме [4]:

42.

5. Найдем из этого равенства квантиль uγ (по
таблице или с помощью компьютерных
вычислений).

43.

6. Решая неравенство
относительно а, получим, что с вероятностью γ
выполняется условие:
Искомый доверительный интервал для
математического ожидания а: