Похожие презентации:
Cтатистическая проверка гипотез. Лекция 8
1. Лекция 8
Cтатистическая проверка гипотез2.
В процессе анализа данных статистического наблюдениявыдвигаются различные предположения вероятностного
характера относительно генеральной совокупности.
Например:
- в качестве возможного выбирается конкретный вид
распределения изучаемого признака, указывается его
аналитическая форма представления;
- исследуемая причинно-следственная связь изображается с
помощью определенной модели, включающей в себя лишь
часть факторных признаков (объявленных в рамках этой
модели наиболее существенными);
- аналитически описывается предполагаемая тенденция
развития процесса т. д.
3.
Подобные суждения, теоретически выражающиестатистические зависимости и закономерности, называются
статистическими гипотезами.
Их проверка заключается в оценке существенности
расхождений между теоретическими и эмпирическими (т.е.
вычисленными по данным наблюдения) показателями с
помощью специальных статистических методов, называемых
критериями согласия.
Надежность оценки характеризуется некоторой
вероятностью.
4.
Обозначим через H0 предположение, подлежащеестатистической проверке.
Тогда H0 называют основной (нулевой) гипотезой.
Пусть H1 — альтернативная гипотеза, конкурирующая с H0
и принимаемая в случае, если в результате статистической
проверки гипотеза H0 отвергается.
5.
Решение о справедливости основной гипотезы H0 илиальтернативной H1 принимается по выборочным данным
(полученным в результате случайного отбора) и, =>, может
быть ошибочным (с некоторой вероятностью):
1) отвергается правильная гипотеза H0 (ошибка первого
рода);
2) принимается неправильная гипотеза H0 (ошибка второго
рода).
6.
Уровень значимости α— вероятность ошибки первого рода.Величина α задается заранее и определяет надежность
принятого решения: с вероятностью γ=1-α верная гипотеза
H0 будет принята.
Вероятность ошибки второго рода обозначается β .
Величина 1-β (мощность критерия) характеризует
вероятность, с которой правильно отвергается неверная
гипотеза H0 .
Между уровнем значимости α и мощностью критерия 1-β
существует связь: с уменьшением уровня значимости α , а
значит, и с уменьшением вероятности появления ошибки
первого рода падает мощность критерия.
В этом случае он все меньше улавливает различие между
нулевой H0 и альтернативной H1 гипотезами.
7.
Поэтому нельзя беспредельно уменьшать риск ошибкипервого рода, т.к. суждения становятся все менее
определенными.
При фиксированном объеме выборки n и заданном уровне
значимости α предпочтительнее более мощный критерий, на
основании которого в большей степени выявляется неверная
гипотеза H0 .
8.
Всякий критерий согласия, служащий для проверкистатистических гипотез, включает в себя переменную
критерия ζ , характеризующую величину суммарных
расхождений теоретических и эмпирических показателей
(параметров).
Множество значений переменной ζ (являющейся по своей
сути случайной величиной) разбивается на следующие
непересекающиеся части:
► критическая область, при попадании ζ в которую
основная гипотеза H0 отвергается и принимается
альтернативная гипотеза H1 ;
► область принятия гипотезы H0 .
9.
Обработка экспериментальных данных с помощью любогокритерия согласия осуществляется по следующей схеме:
1. Берется один или два ряда наблюдений (одна или две
выборки) и по элементам этих рядов по определенным
формулам вычисляют переменную критерия ζ .
2. По заданному уровню значимости α и числу степеней
свободы k находят по таблицам приложений критическую
область значений ζ.
3. Если полученная в пункте 1 переменная ζ попадает в
критическую область, то гипотеза H0 отвергается,
принимается конкурирующая гипотеза H1 .
10.
4. Если при проверке гипотезы найденная по выборочнымданным ζ не попадает в критическую область, то нет
достаточных оснований отвергнуть выдвинутую гипотезу H0.
Т.е. гипотеза H0 не отвергается, но это не означает, что H0
является единственно подходящей гипотезой: просто H0 не
противоречит результатам выборочного наблюдения.
Однако таким же свойством могут обладать наряду с H0 и
другие гипотезы.
11.
Оценка статистической значимости коэффициентакорреляции
Проверяется следующая основная гипотеза H0 : rген = 0 (о
равенстве нулю генерального коэффициента корреляции, т.е.
об отсутствии линейной зависимости между признаками X и
Y в генеральной совокупности) при конкурирующей гипотезе
H1 : rген ≠0 .
При большом объеме выборки n, отобранной из генеральной
нормально распределенной совокупности, статистическая
значимость коэффициента корреляции rXY проверяется на
основе критерия Стьюдента.
12.
В качестве переменной критерия принимается величинаимеющая распределение Стьюдента с k=n-2 степенями
свободы.
13.
Применение критерия Стьюдента к проверке гипотезы H0 оравенстве нулю генерального коэффициента корреляции
осуществляется по правилу:
1. По найденному выборочному коэффициенту корреляции
rXY вычислить величину ζрасч :
14.
2. По заданному уровню значимости α=1-γ и числу степенейсвободы k=n-2 определить по таблице распределения
Стьюдента критическое значение tкр.
3. Если ζрасч > tкр , то гипотеза H0 отвергается, принимается
конкурирующая гипотеза H1 и, =>, полученный коэффициент
корреляции rXY статистически значим.
4. В случае ζрасч ≤ tкр нет достаточных оснований отвергнуть
выдвинутую гипотезу H0 и, =>, данный коэффициент
корреляции rXY статистически незначим, а полученная
линейная регрессия не может быть использована как
статистическая модель исследуемой взаимосвязи между
признаками X и Y.
15.
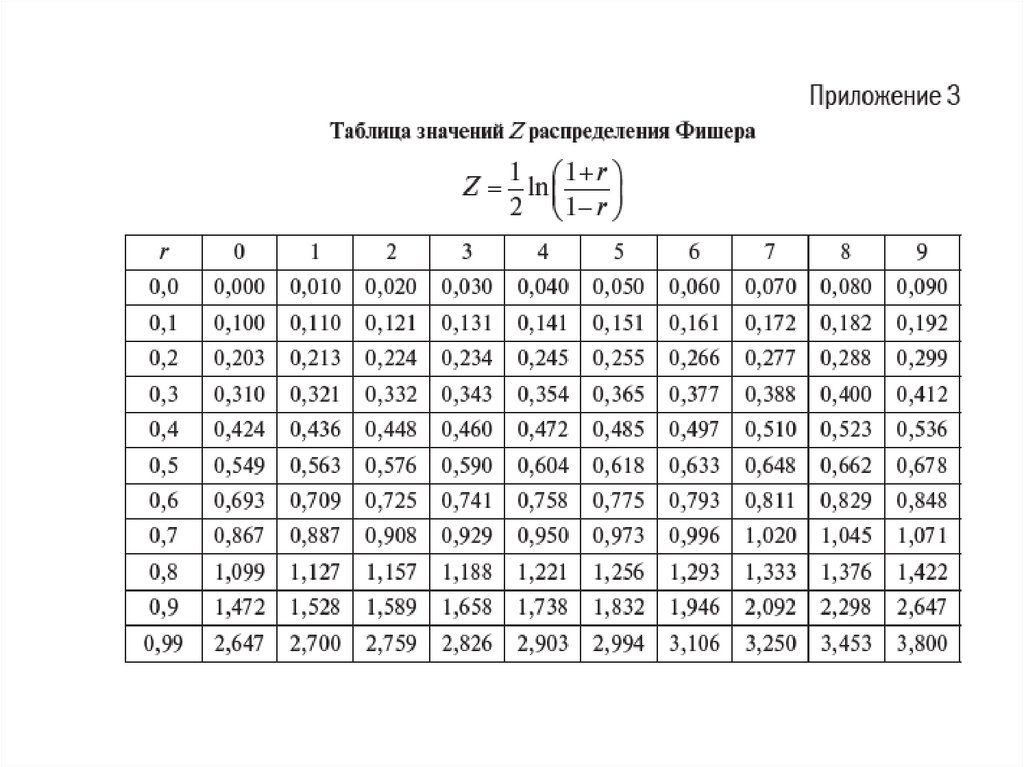
Если коэффициент корреляции по модулю близок к единице( rXY >0,8), получен по данным относительно малой выборки
(n < 30 ), то проверка статистической значимости
производится с помощью распределения Фишера:
Средняя квадратическая ошибка распределения Фишера:
16.
Если отношение ׀z׀/σ(z)> 3 (при уровне значимости α =0,01),то найденный коэффициент корреляции статистически
значим;
в противном случае — статистически незначим.
Величина z определяется по таблице значений распределения
Фишера.
17.
Задача 1По выборке объема n = 60, извлеченной из двумерной
нормальной генеральной совокупности (X,Y), найден
коэффициент корреляции rXY =0,747 .
Проверить статистическую значимость с вероятностью γ
=0,95 найденного коэффициента корреляции rXY .
Решение
Поскольку n = 60 , rXY =0,747 , то:
Заданный уровень значимости α=1-γ=1-0,95=0,05, число
степеней свободы k=n-2=60-2= 58 .
18.
Тогда по таблице распределения Стьюдента находим t = 2,0.Поскольку ζрасч > tкр , то найденный коэффициент корреляции
статистически значим (с вероятностью γ =0,95), т.е. X и Y
коррелированны.
19.
Задача 2По выборке объема n =10, извлеченной из двумерной
нормальной генеральной совокупности (X,Y), найден
коэффициент корреляции rXY = -0,926.
Проверить статистическую значимость найденного
коэффициента корреляции rXY при уровне значимости
α =0,01.
Решение
Поскольку выборка малая (n = 10, т.е. n < 30),
ǀrXY ǀ =0,926>0,8,
то значимость проверяем с помощью распределения Фишера.
20.
По таблице значений распределения Фишера для rXY = -0,926имеем z = -1,658.
Средняя квадратическая ошибка распределения Фишера:
Вычислим отношение ׀z׀/σ(z)=1,658/0,378=4,387 .
Заданный уровень значимости α =0,01.
Поскольку ׀z׀/σ(z)=4,387, а это > 3,
то найденный коэффициент корреляции статистически
значим.
21.
Статистическая проверка гипотезы о теоретическомраспределении
Выбор теоретического распределения в качестве
математической модели, выражающей закономерность
распределения изучаемого признака, производится на основе
графических изображений данного вариационного ряда
(полигон, гистограмма) и вычисленных статистических
показателей (сренее, среднее квадратическое отклонение σ),
характеризующих форму и тип кривой распределения.
В результате устанавливают конкретный закон
распределения, представимый аналитически через функцию
распределения F(x) или функцию плотности f(x).
22.
На следующем этапе анализа статистических данныхнеобходимо произвести проверку соответствия найденного
теоретического распределения эмпирическому.
При большом объеме выборки n ≥100 и больших частотах
ni ≥ 5 вариант признака гипотеза о соответствии найденного
теоретического распределения эмпирическому проверяется
на основе критерия согласия χ2 Пирсона.
В качестве переменной критерия χ2 принимается мера
расхождения наблюдаемых частот ni и теоретических частот
n'i :
имеющая распределение χ2 с k степенями свободы.
23.
Применение критерия χ2 к проверке гипотезы о соответствиинайденного теоретического распределения эмпирическому
осуществляется по правилу:
1. Разбить числовую ось на s промежутков: (-∞; а1), [а1; а2),…
[аs-1, +∞).
2. Рассчитать теоретические частоты n'i, определяющие
возможные численности каждого промежутка данного
вариационного ряда при предположении о распределении
признака по выбранному теоретическому закону f(x):
n'i =nPi, i=1,2,...,s,
где n — объем совокупности,
Pi =P(ai-1 ≤ x < ai ) — вероятность попадания в интервал
(ai-1 ; ai) значений признака.
24.
В частности, если в качестве теоретического выбранонормальное распределение с параметрами (a, σ2),
то Pi =Ф(ui) - Ф(ui-1),
где Ф(u) — функция Лапласа;
ui — границы интервала
25.
Если изучаемый признак X является дискретными x1, x2, …, xs — его наблюдаемые значения,
то Pi=P(X=xi), i=1,2,...,s.
Например, при выборе в качестве теоретического
распределение Пуассона с параметром λ имеем
где xi — неотрицательные числа.
26.
3. Вычислить величину переменной критерия:Сравнивая наблюдаемые ni и n'i теоретические частоты,
получаем, что близость их значений говорит в пользу
гипотезы о распределении признака в генеральной
совокупности по теоретическому закону f(x).
Заметные различия отвергают эту гипотезу.
27.
4. Определить число степеней свободы k по формулеk=s-l -1 ,
где s — число интервалов;
l — число параметров теоретического закона f(x),
вычисляемых с помощью эмпирического распределения,
в частности:
► для нормального распределения k=s-3, т.к. по
вариационному ряду рассчитываются два параметра:
► для распределения Пуассона k=s-2, т.к. по вариационному
ряду рассчитывается один параметр
28.
5. По заданному уровню значимости α и числу степенейсвободы k определить по таблице распределения χ2
критическое значение χ2кр.
6. Если χ2расч > χ2кр, т.е. χ2 попадает в критическую область,
то оцениваемое расхождение наблюдаемых частот ni и
теоретических частот n'i существенно,
и его нельзя объяснить случайностью выбранных данных.
Тогда гипотеза о распределении признака в генеральной
совокупности по теоретическому закону f(x) отвергается.
29.
7. В случае c χ2расч ≤ χ2кр,то оцениваемое расхождение несущественно
и может быть объяснено случайностью выбранных данных.
В такой ситуации гипотеза о распределении признака в
генеральной совокупности по теоретическому закону f(x)
принимается (не отвергается).





























 Математика
Математика








