Похожие презентации:
Треугольник. Равенство треугольников
1.
2.
Треугольник-- геометрическая фигура, состоящая
из трех точек, не лежащих на одной
прямой и соединенных попарно
отрезками
Точки А, В и С – вершины треугольника
В
Отрезки АВ, ВС и АС –
стороны треугольника
АВС, ВАС, ВСА –
углы треугольника
Р АВС
= АВ + ВС + АС
периметр треугольника
А
С
3.
E•Назовите углы ∆ DEK, прилежащие к стороне
EK, DE, DK.
D
K
S
•Назовите угол ∆ DEK, заключенный между
сторонами DE и DK, EK и DE.
•Между какими сторонами ∆ DEK заключен
угол К?
P
M
3
4.
Два треугольника называются равными, если их можносовместить наложением.
Если два треугольника равны, то элементы (т.е.
стороны и углы)
одного треугольника соответственно равны
элементам другого треугольника.
S
В
АВС = MSN
А
М
С
N
5.
Равенство треугольниковДва треугольника равны, если
каждый из них можно наложить на
другой так, что их вершины и
стороны попарно совместятся.
B1
B
Если треугольники равны, то
элементы одного треугольника
соответственно равны элементам
другого треугольника
C1
AB = A1B1, BC = B1C1, CA = C1A1
A1
A = A1, B = B1, C = C1
C
A
6.
BВ равных треугольниках против равных углов
лежат равные стороны
И наоборот, против равных
сторон лежат равные углы
B1
А
C
A1
C1
7.
Признак – показатель, примета, знак, по которым можноузнать, определить что–нибудь. Различительные признаки:
признаки пола, признаки весны, признаки делимости и т.п.
В геометрии некоторое условие, при которых два
заданных треугольника оказываются равными, называется
признаком равенства треугольников
В математике каждое утверждение, справедливость которого
устанавливается путем рассуждений, называется теоремой,
а сами рассуждения называются доказательством теоремы.
Условие – это уже известные факты, о которых говориться в
теореме, а заключение – это то, что нужно получить, доказать.
7
8.
Теорема.Если две стороны и угол между ними одного треугольника
равны соответственно двум сторонам и углу между ними другого
треугольника , то такие треугольники равны.
Дано : АВС , А1В1С1, АВ А1В1, АС А1В1
ВАС В1 А1С1
Доказать: ∆ АВС = ∆ А1В1С1..
8
9. Доказательство.
910. Применение первого признака равенства треугольников при решении задач.
Являются ли АВС и FDE равными?10
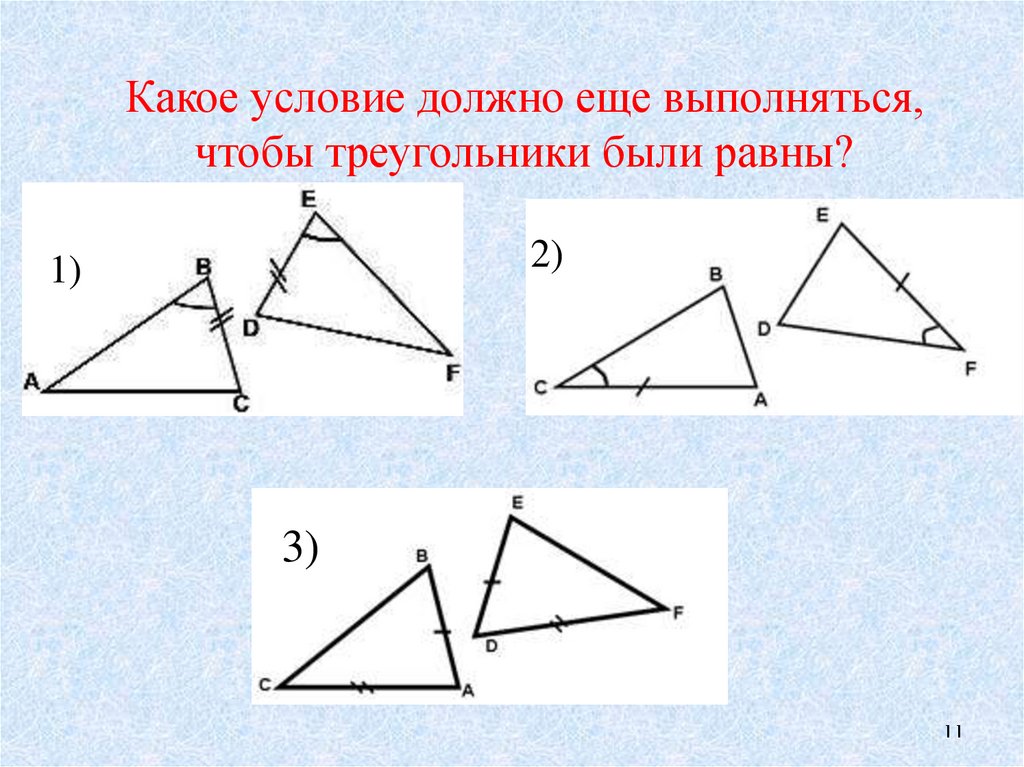
11. Какое условие должно еще выполняться, чтобы треугольники были равны?
2)1)
3)
11
12. Задача
На рисунке точка О — серединаотрезков АВ и РТ. Докажите, что
∆ АОТ = ∆ ВОР.
Дано: АВ ∩ РТ = О
О — середина отрезков АВ и РТ.
Доказать: ∆ АОТ = ∆ ВОР
ОВ
ОР
АВ
РТ
РОВ
ОР
∆ ВОР
ВОР
углу между ними
12











 Математика
Математика