Похожие презентации:
Треугольник. Первый признак равенства треугольников
1. Треугольник. Первый признак равенства треугольников
МБОУ СОШ №22г. Нижний Новгород
Лапкина О.А.
Треугольник.
Первый признак равенства
треугольников
2.
3.
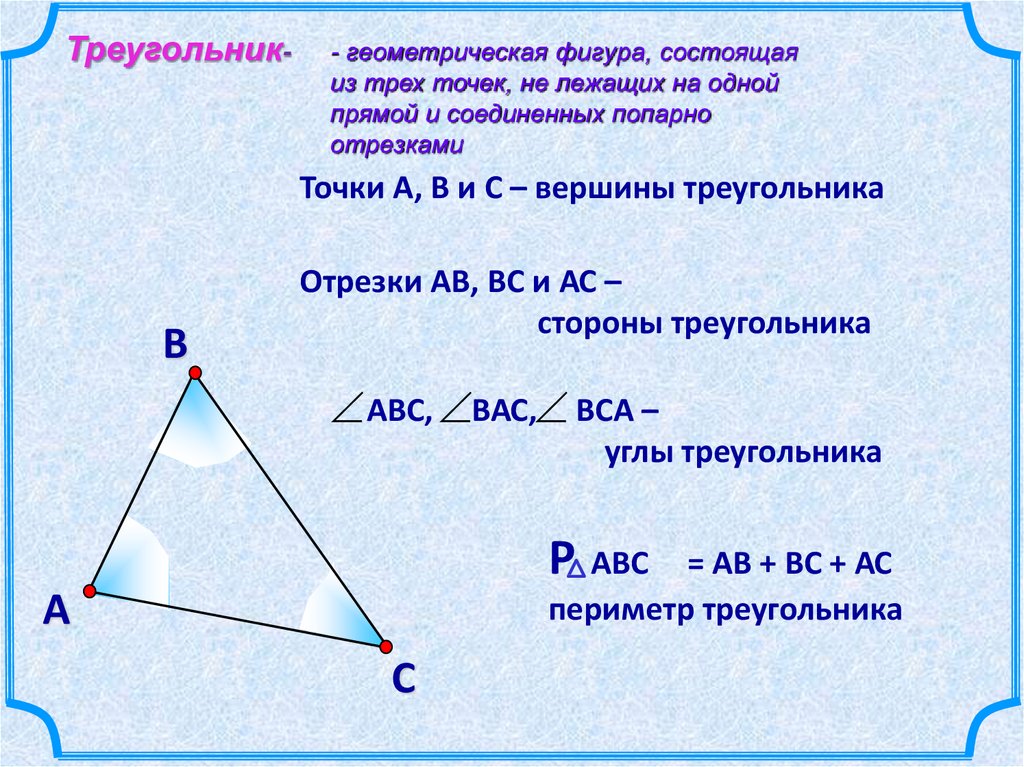
Треугольник-- геометрическая фигура, состоящая
из трех точек, не лежащих на одной
прямой и соединенных попарно
отрезками
Точки А, В и С – вершины треугольника
В
Отрезки АВ, ВС и АС –
стороны треугольника
АВС, ВАС, ВСА –
углы треугольника
Р АВС
= АВ + ВС + АС
периметр треугольника
А
С
4.
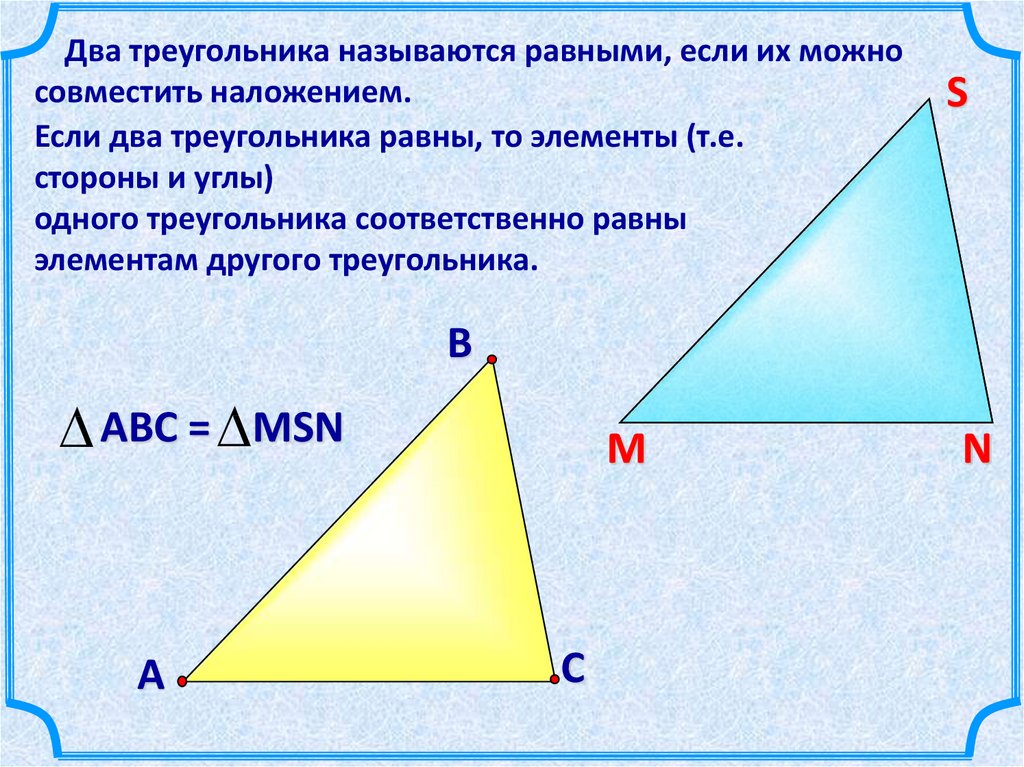
Два треугольника называются равными, если их можносовместить наложением.
Если два треугольника равны, то элементы (т.е.
стороны и углы)
одного треугольника соответственно равны
элементам другого треугольника.
S
В
АВС = MSN
А
М
С
N
5.
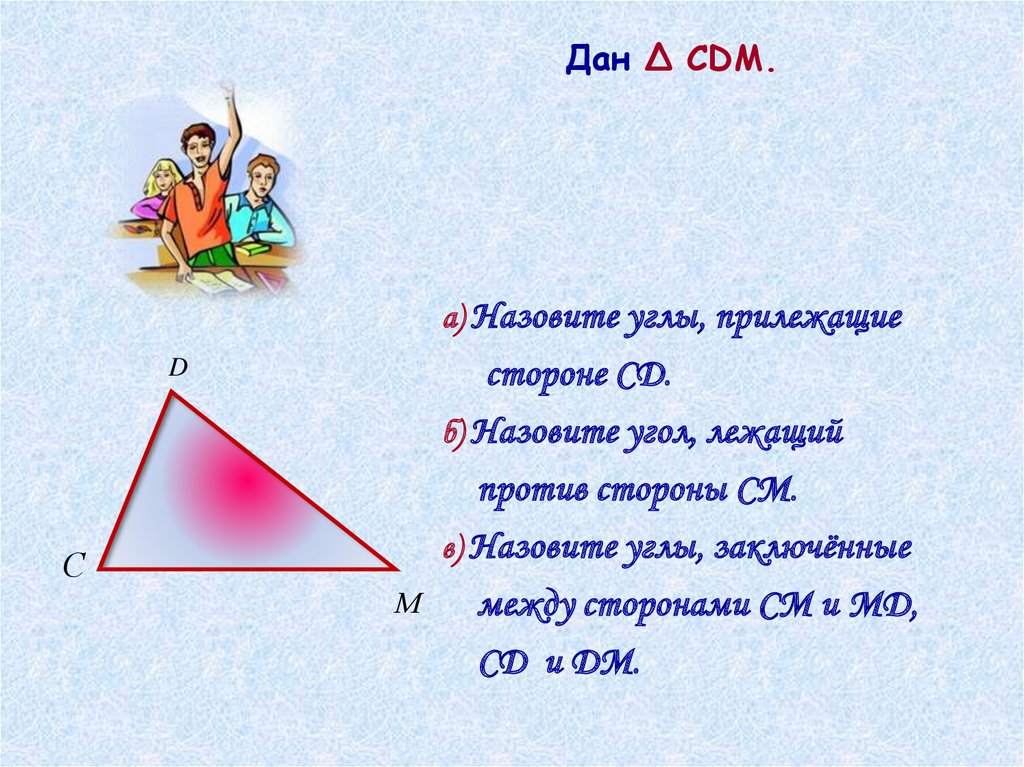
Дан Δ CDM.а) Назовите углы, прилежащие
D
С
М
стороне CD.
б) Назовите угол, лежащий
против стороны СМ.
в) Назовите углы, заключённые
между сторонами СМ и MD,
CD и DM.
6.
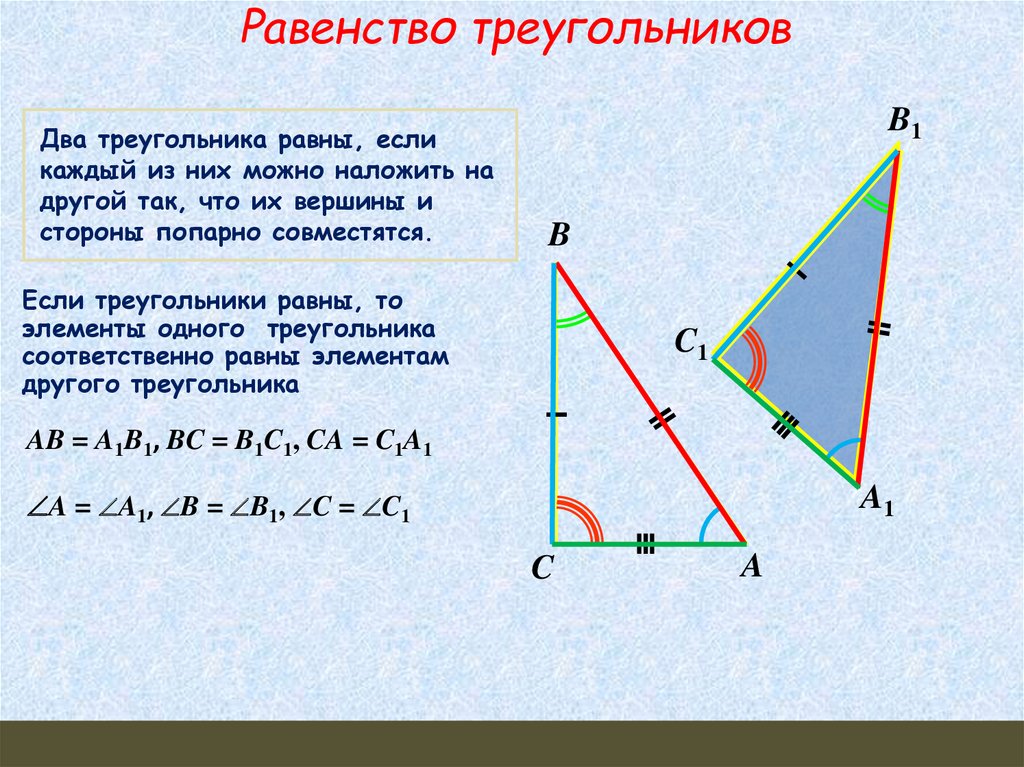
Равенство треугольниковДва треугольника равны, если
каждый из них можно наложить на
другой так, что их вершины и
стороны попарно совместятся.
B1
B
Если треугольники равны, то
элементы одного треугольника
соответственно равны элементам
другого треугольника
C1
AB = A1B1, BC = B1C1, CA = C1A1
A1
A = A1, B = B1, C = C1
C
A
7.
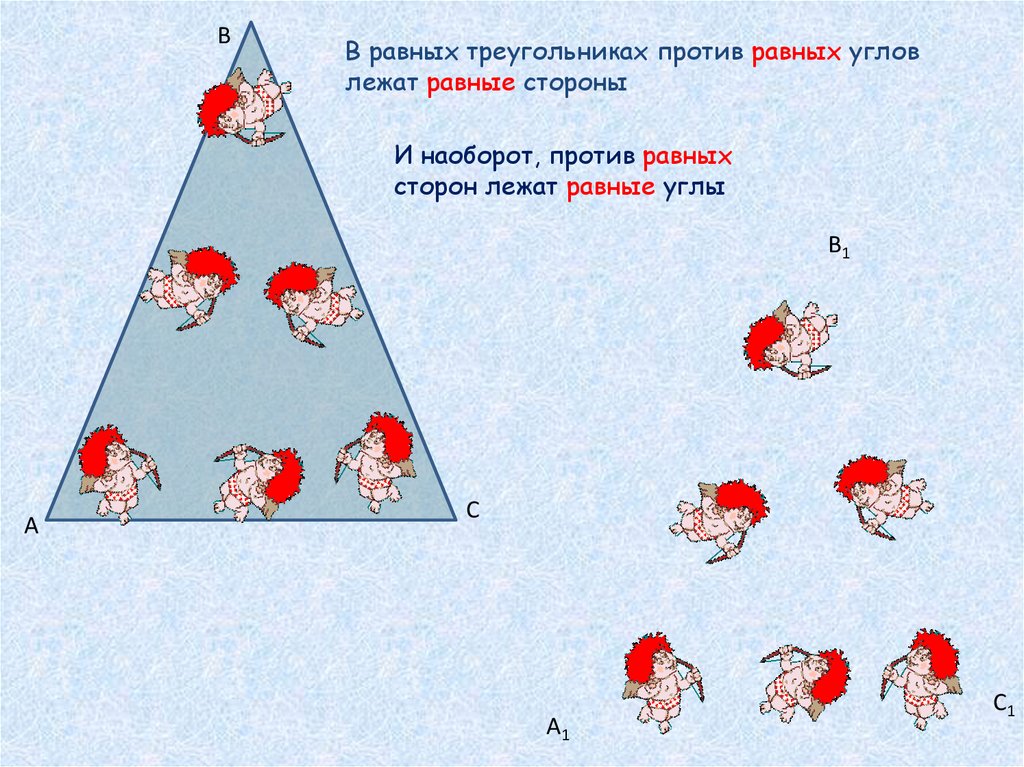
BВ равных треугольниках против равных углов
лежат равные стороны
И наоборот, против равных
сторон лежат равные углы
B1
А
C
A1
C1
8.
Дадим определение теоремы иаксиомы
Теорема - это высказывание, правильность
которого установлена при помощи
рассуждения, доказательства.
Аксиома - это первоначальные факты геометрии,
которые принимаются без доказательства.
9.
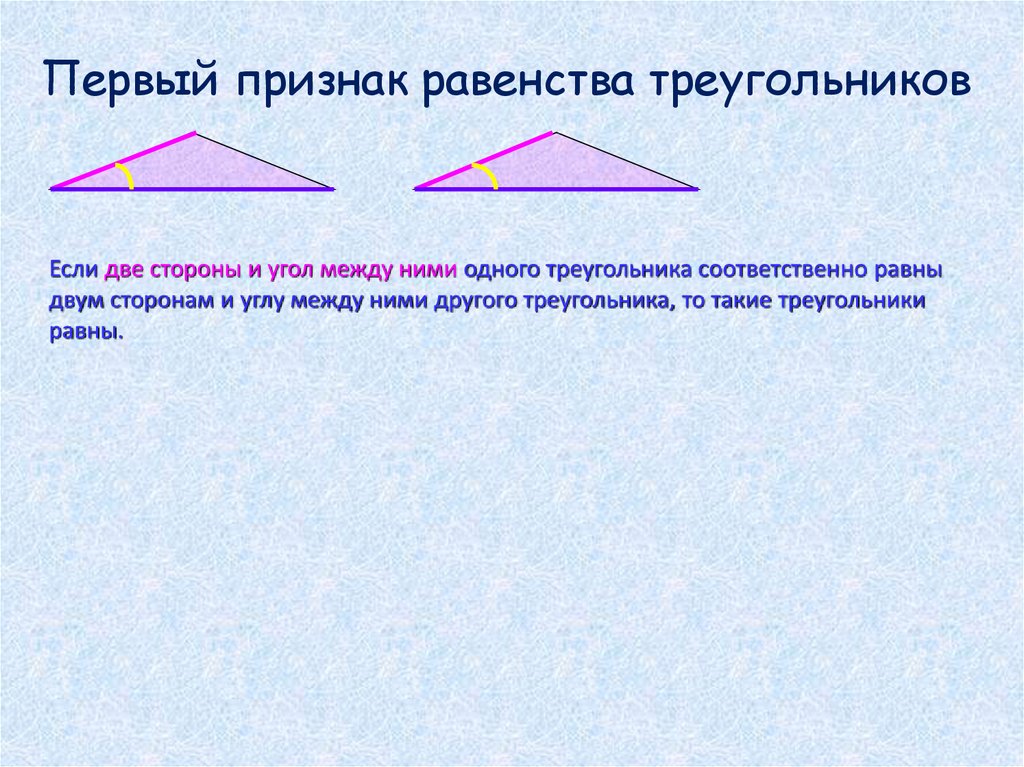
Первый признак равенства треугольниковЕсли две стороны и угол между ними одного треугольника соответственно равны
двум сторонам и углу между ними другого треугольника, то такие треугольники
равны.
10.
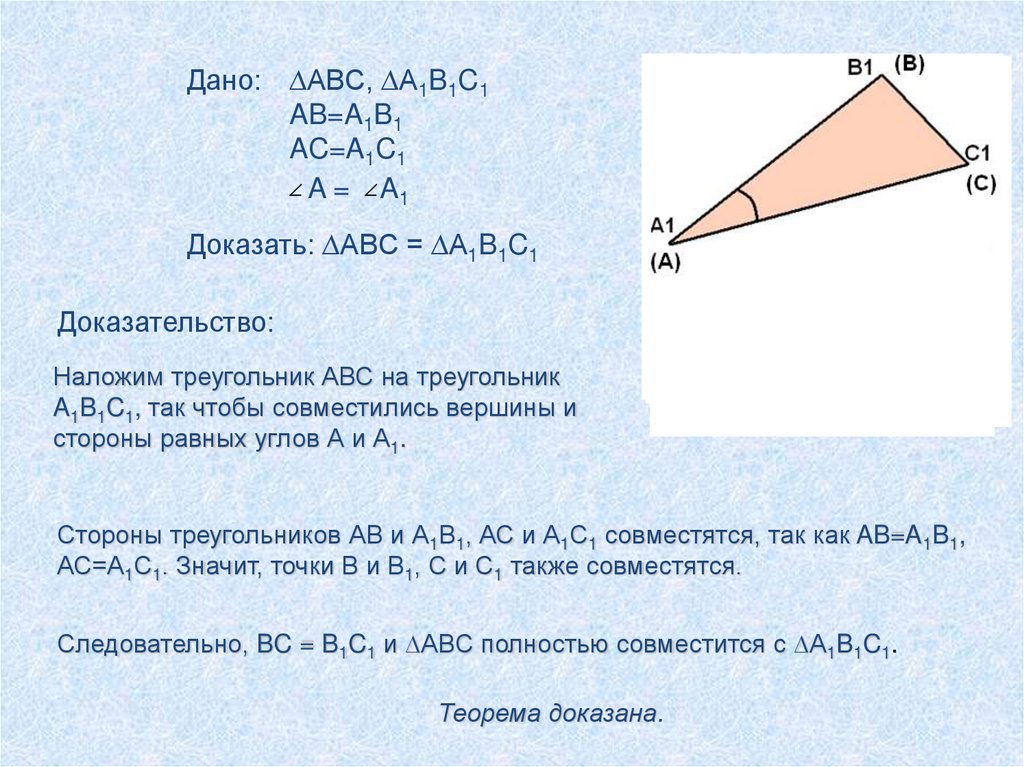
Дано: ∆ABC, ∆A1B1C1AB=A1B1
AC=A1C1
A = A
1
Доказать: ∆ABC = ∆A1B1C1
Доказательство:
Наложим треугольник АВС на треугольник
A1B1C1, так чтобы совместились вершины и
стороны равных углов А и А1.
Стороны треугольников АВ и А1В1, АС и А1С1 совместятся, так как AB=A1B1,
АС=А1С1. Значит, точки В и В1, С и С1 также совместятся.
Следовательно, BC = B1C1 и ∆ABC полностью совместится с ∆A1B1C1.
Теорема доказана.
11.
В2
А
С
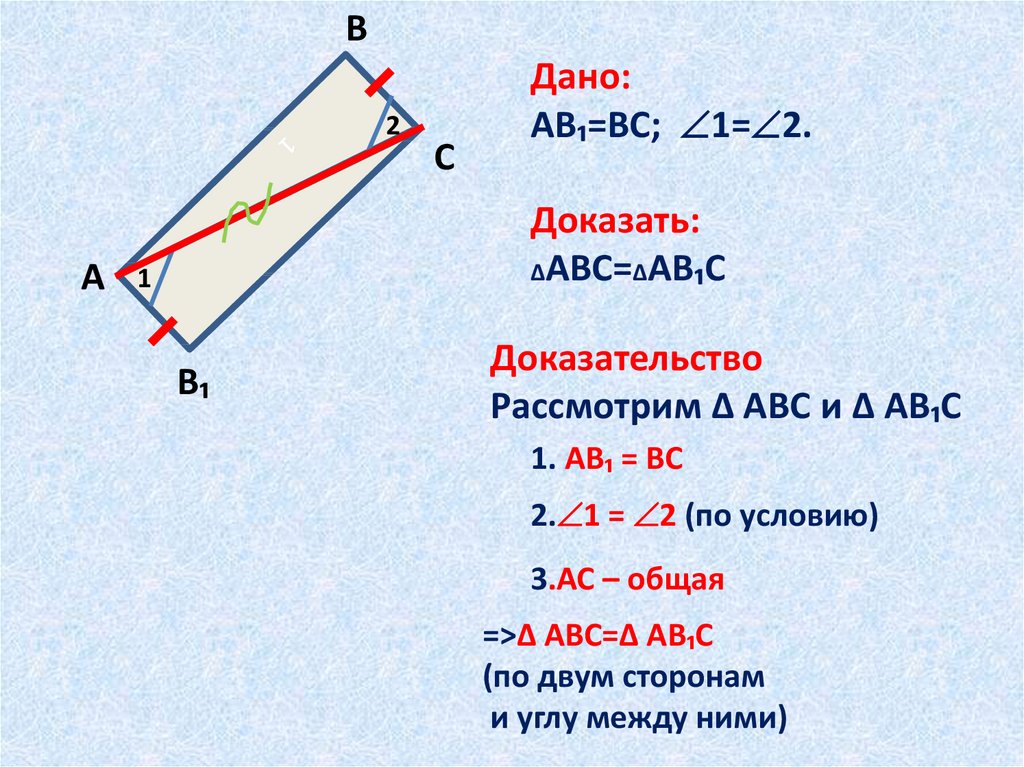
Дано:
АВ₁=ВС; 1= 2.
Доказать:
∆АВС=∆АВ₁С
1
В₁
Доказательство
Рассмотрим ∆ АВС и ∆ АВ₁С
1. АВ₁ = ВС
2. 1 = 2 (по условию)
3.АС – общая
=>∆ АВС=∆ АВ₁С
(по двум сторонам
и углу между ними)
12.
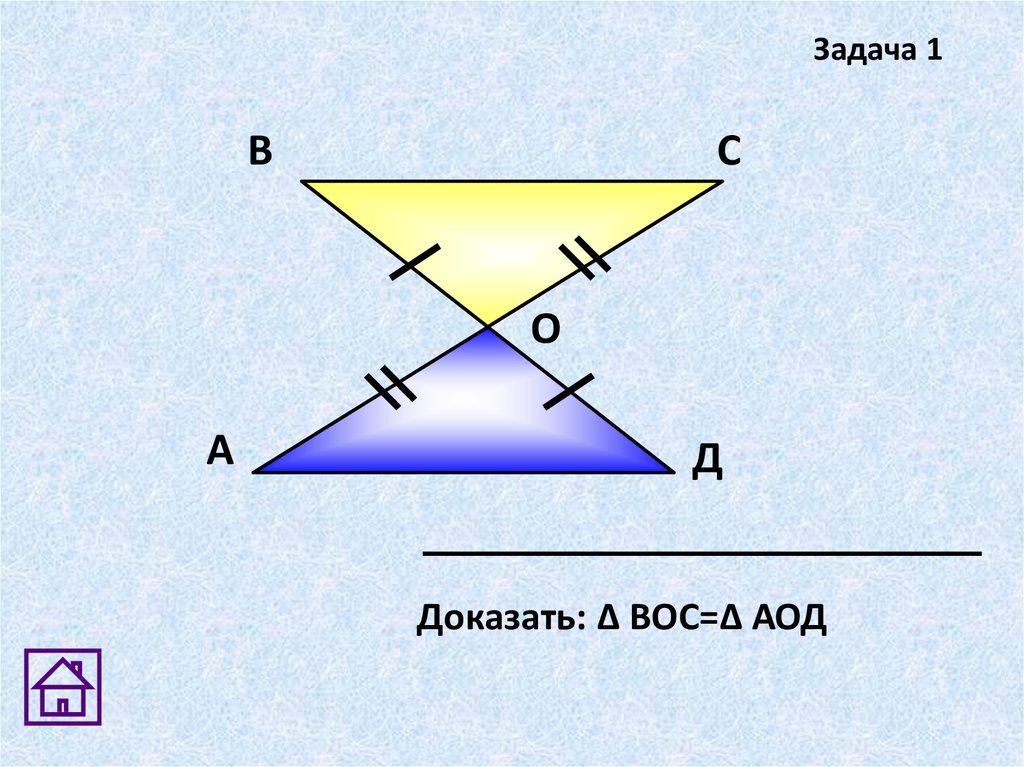
Задача 1В
С
О
А
Д
Доказать: Δ ВОС=Δ АОД
13.
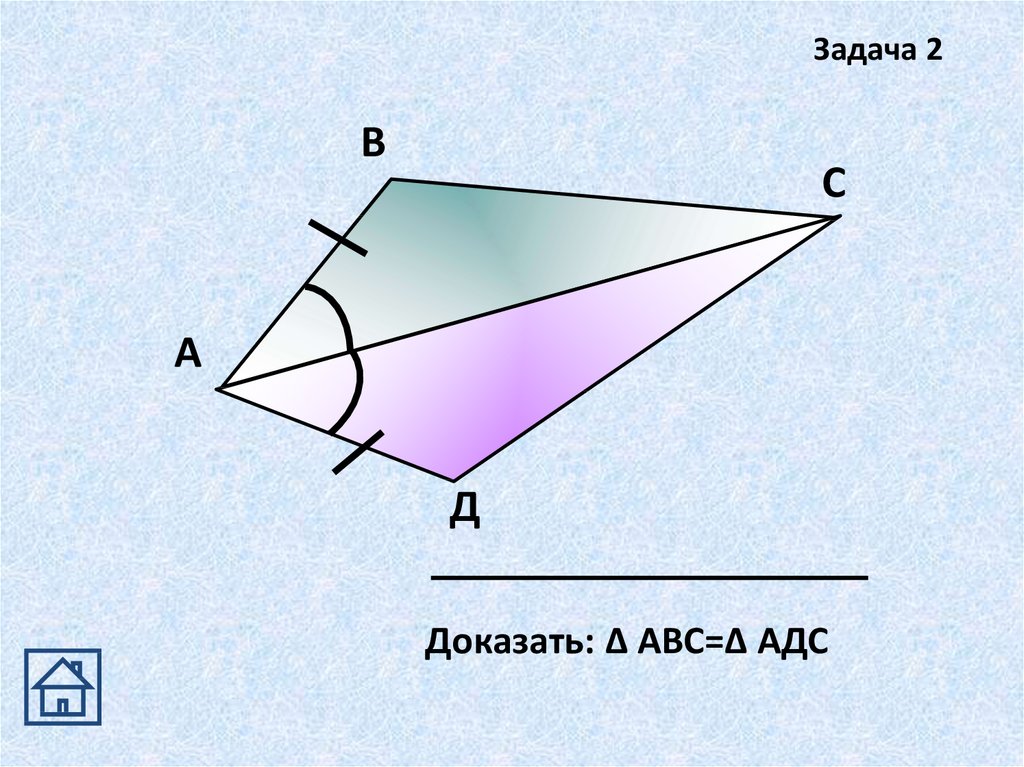
Задача 2В
С
А
Д
Доказать: Δ АВС=Δ АДС
14.
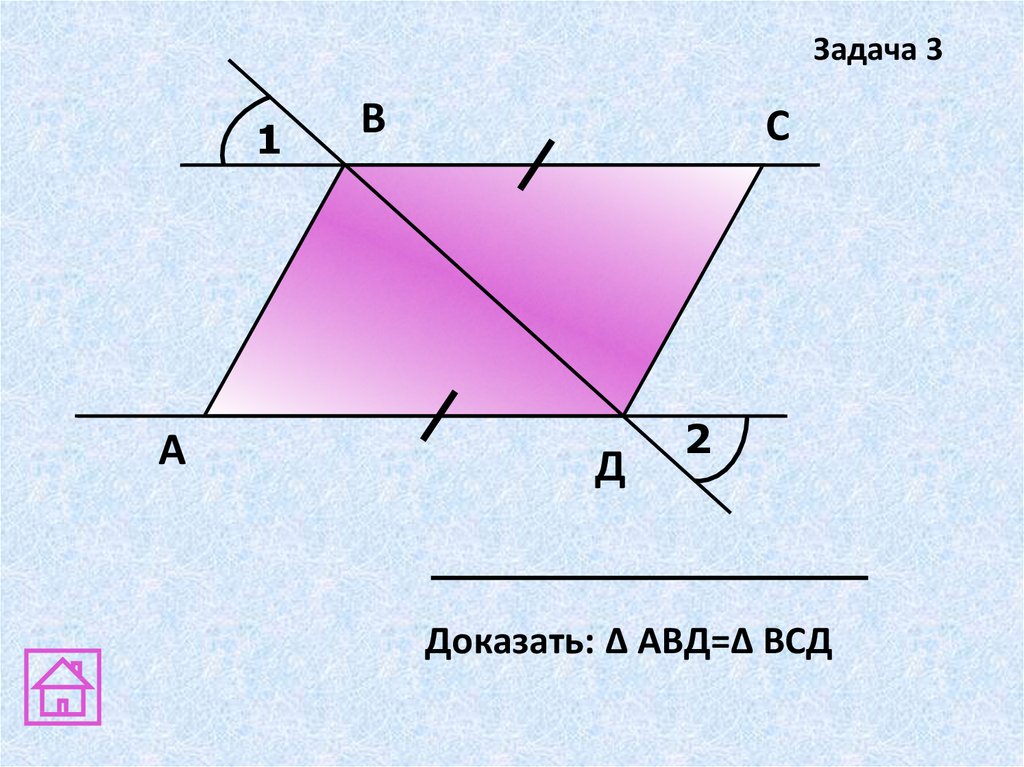
Задача 31
А
В
С
Д
2
Доказать: Δ АВД=Δ ВСД
15.
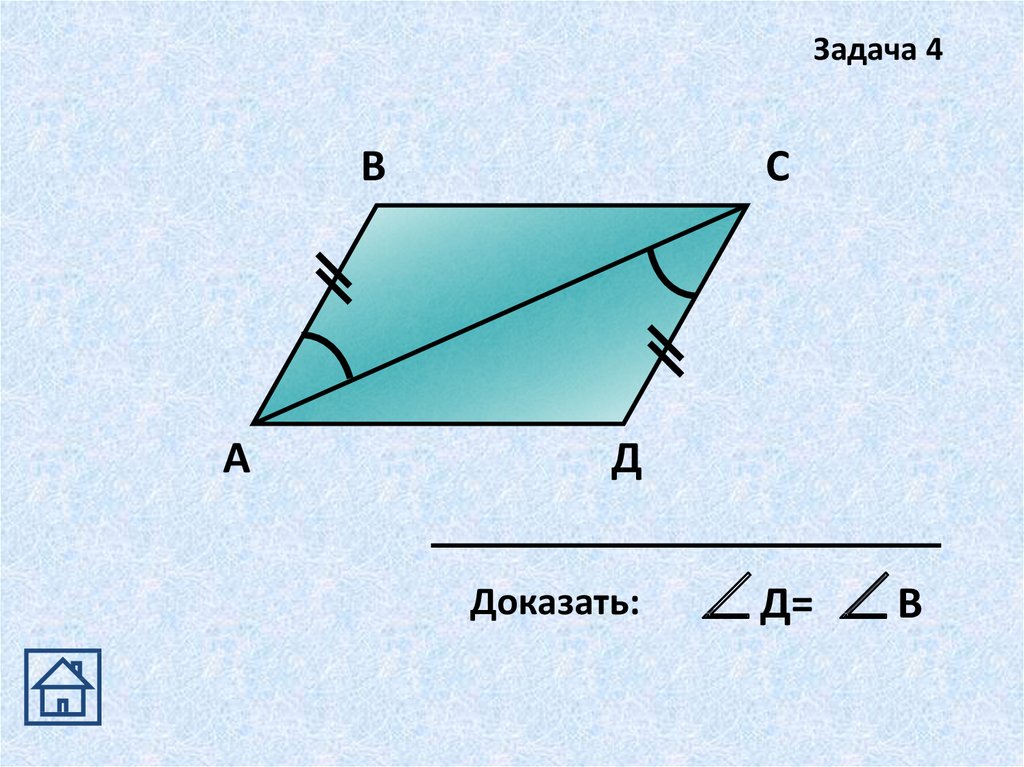
Задача 4В
А
С
Д
Доказать:
Д= В
16.
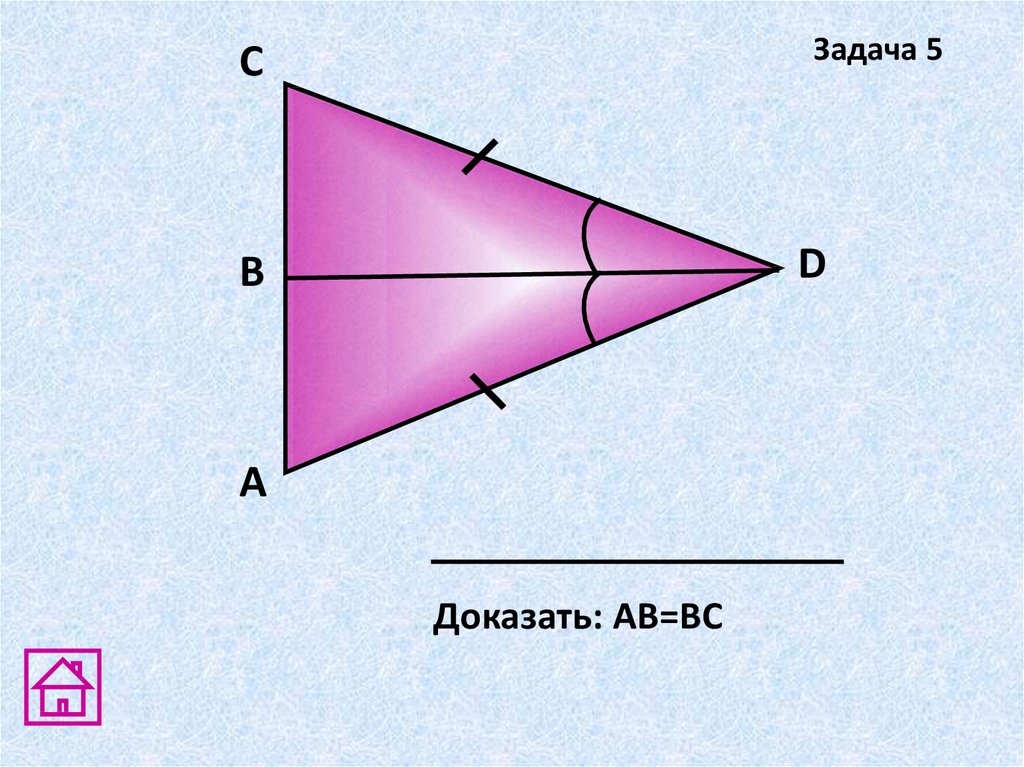
Задача 5C
D
В
А
Доказать: АВ=ВС
17.
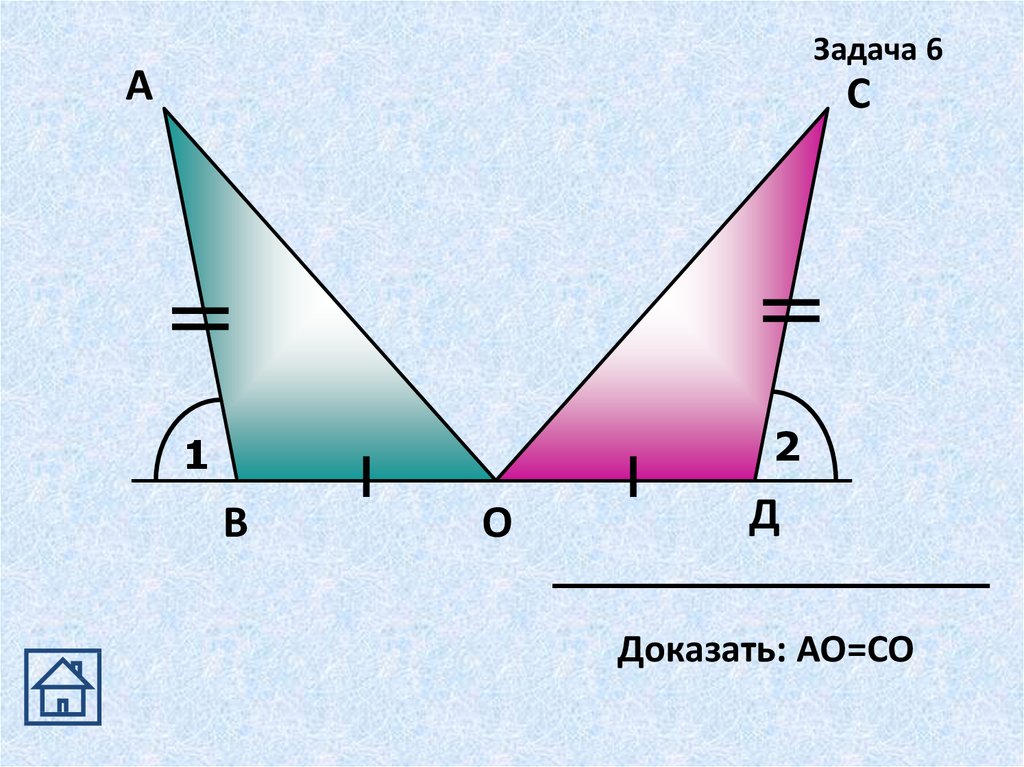
Задача 6А
С
2
1
В
О
Д
Доказать: АО=СО
18.
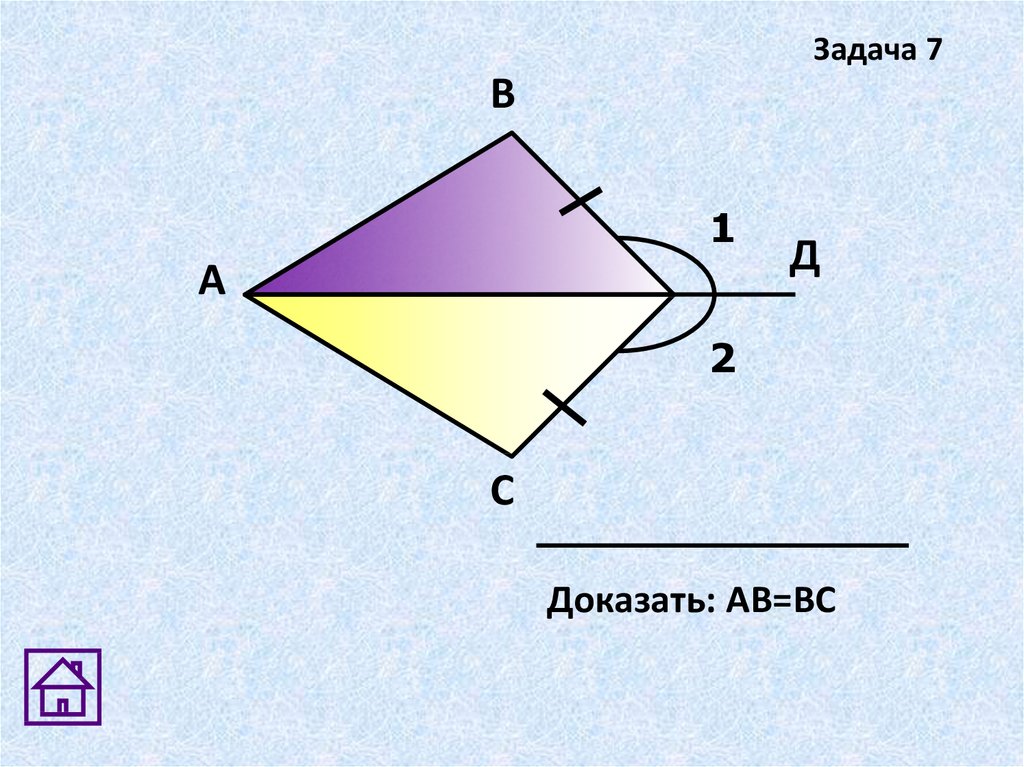
Задача 7В
1
А
Д
2
С
Доказать: АВ=ВС
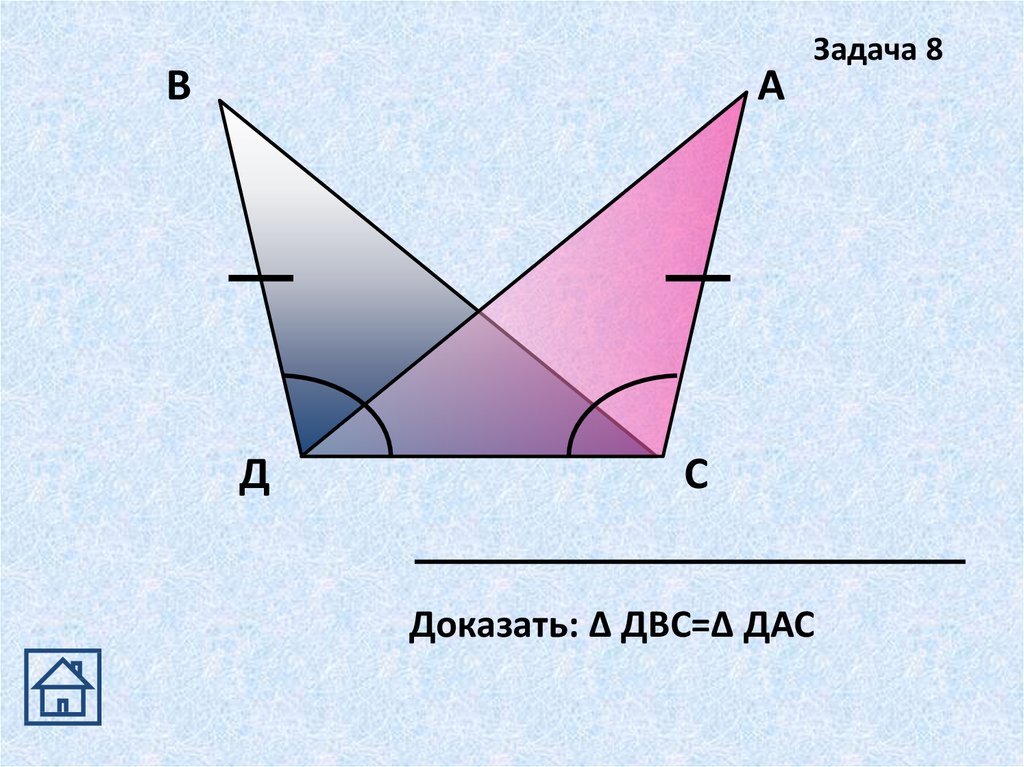
19.
ВА
Д
Задача 8
С
Доказать: Δ ДВС=Δ ДАС
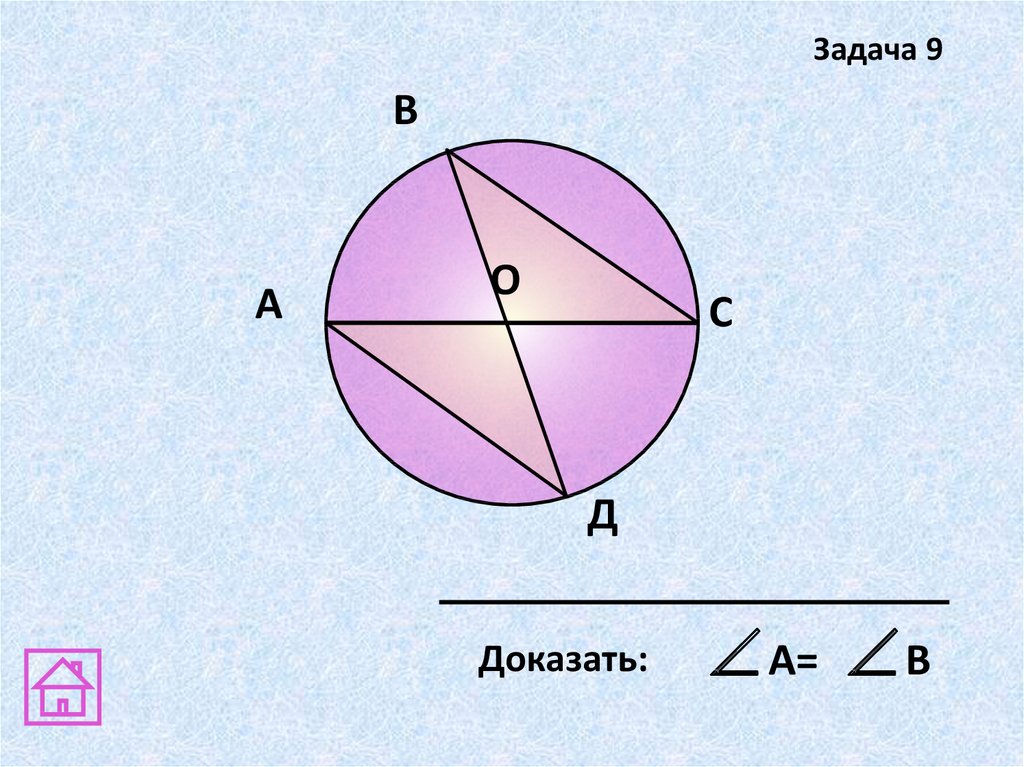
20.
Задача 9В
А
О
C
Д
Доказать:
А= В
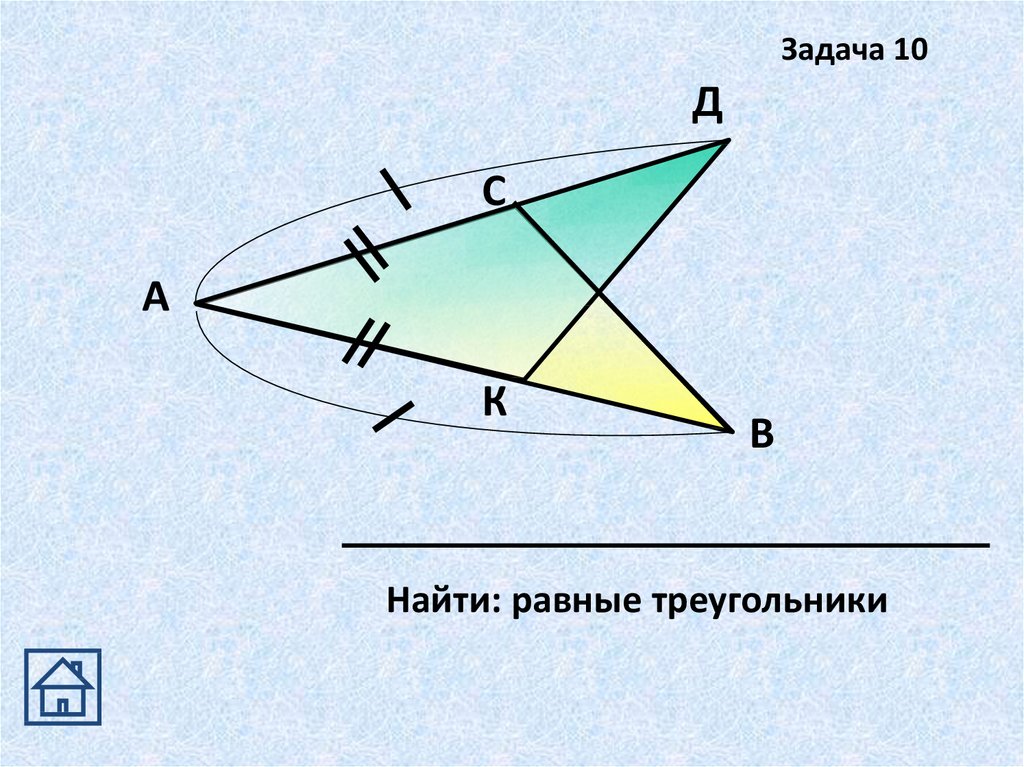
21.
Задача 10Д
С
А
К
В
Найти: равные треугольники


 Математика
Математика