Центр тяжести (1)

1. Государственное бюджетное образовательное учреждение среднего профессионального образования «Петровский колледж»

занятие
по дисциплине
ТЕХНИЧЕСКАЯ МЕХАНИКА
Разработала: преподаватель
технической механики
Голубева Оксана Александровна
г. Санкт- Петербург, 2021

2. учебное занятие «ЦЕНТР ТЯЖЕСТИ»

3. Межпредметные связи

Обеспечивающие
Математика
Физика
Материаловедение
Инженерная графика
Обеспечиваемые
- ПМ.01. Подготовка и осуществление технологических
процессов изготовления сварных конструкций
- ПМ.02.Разработка технологических процессов
проектирования изделий
- ПМ.05. Выполнение работ по одной или нескольким
профессиям рабочих должностям служащих

4. Внутрипредметные связи

Раздел: Теоретическая механика
Темы: Основные понятия и аксиомы статики
Плоская система сходящихся сил.
Плоская система произвольно расположенных сил.
Пространственная система сил.
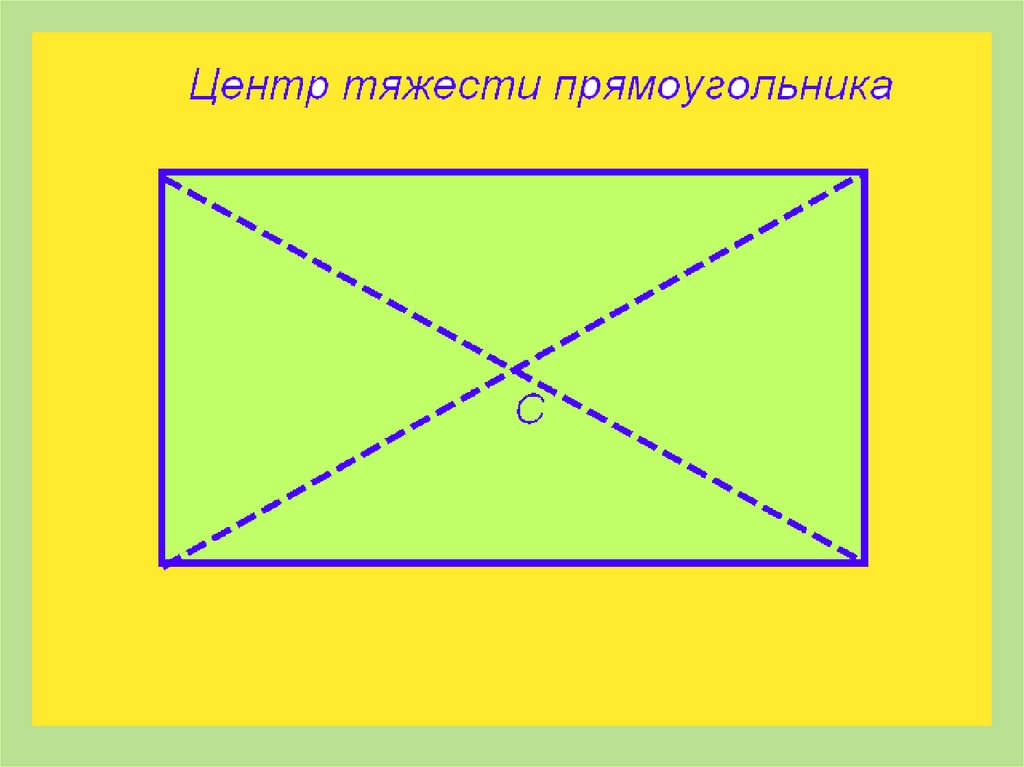
Кинематика точки
Простейшие движения твердого тела
Сложное движение точки
Основные понятия и аксиомы динамики
Метод кинетостатики для материальной точки
Трение. Работа и мощность
Теоремы динамики
Раздел: Сопротивление материалов
Геометрические характеристики плоских сечений
Раздел: Детали машин

5. Место занятия в учебном курсе У каждого предмета есть центр тяжести. Умение определять центр тяжести сложного сечения

6. Тип учебного занятия УЧЕБНОЕ ЗАНЯТИЕ в СДО

7. Организационная форма проведения учебного занятия Лекция

8. Изучение нового материала

Перечень вопросов , подлежащих
изучению
1.Сила тяжести как равнодействующая
вертикальных сил.
2.Центр тяжести. Методы нахождения.
3. Центр тяжести простых
геометрических фигур

9.

1.Сила тяжести как
равнодействующая
вертикальных сил.
Урок .ppt

10.

11.

12.

Сила тяжести – это сила, с
которой тела притягиваются к
земле
Сила тяжести тела – это
равнодействующая сил тяжести
отдельных частиц тела; модуль
этой силы – вес тела.
G – сила тяжести.

13. Сила тяжести

14.

15.

2.Центр тяжести.
Методы нахождения

16.

Центр тяжести тела – это такая
неизменно связанная с этим телом точка,
через которую проходит линия действия
силы тяжести данного тела при любом
положении тела в пространстве.

17. Методы определения центра тяжести тела

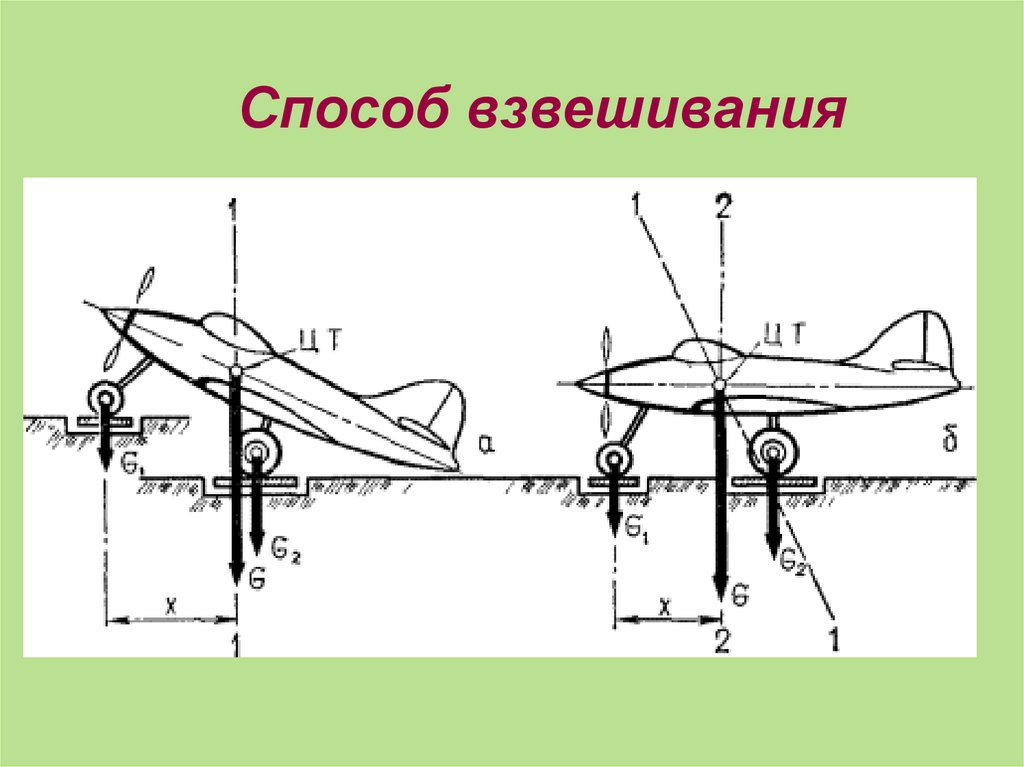
- Способ подвешивания;
- Способ взвешивания;
- Аналитический способ.

18.

Способ взвешивания

19.

Способ взвешивания

20. Аналитический способ

1 Метод симметрии
2 Метод разделения
(разбиения)
3 Метод отрицательных масс

21. .

1 Метод симметрии
1.1 Если однородное тело имеет плоскость
симметрии, то центр тяжести лежит в этой
плоскости

22.

1.2 Если однородное тело имеет ось симметрии,
то центр тяжести лежит на этой оси. Центр
тяжести однородного тела вращения лежит на
оси вращения.
1.3 Если однородное тело имеет две оси
симметрии, то центр тяжести находится в
точке их пересечения.

23. 2 Метод разделения (разбиения)

Тело разбивается на наименьшее
число частей, силы тяжести и
положение центров тяжести
которых известны

24. 3 Метод отрицательных масс

При определении центра
тяжести тела, имеющего
свободные полости, следует
применять метод разбиения, но
массу свободных полостей
считать отрицательной.

25. Координаты центра тяжести тела

n
Xс
GiXi
n
n
GiZi
GiYi
i 1
n
Zс i 1n
Yс i 1n
i 1
i 1
i 1
Gi
Gi
Gi
Xc, Yc, Zc – координаты центра тяжести тела;
Xi ,Yi , Zi – координаты i- ой частицы;
Gi - сила тяжести i- ой частицы тела

26.

3.Центр тяжести
простых
геометрических
фигур

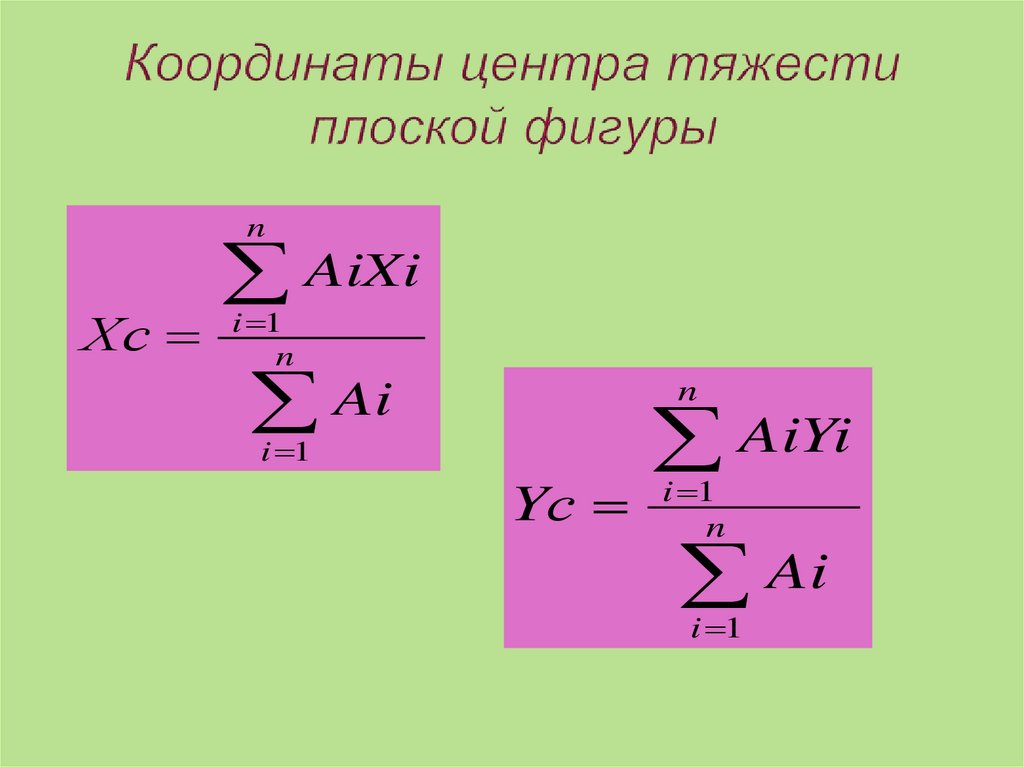
27. Координаты центра тяжести плоской фигуры

n
AiXi
Хс i 1n
Ai
i 1
n
AiYi
Yс i 1n
Ai
i 1

28.

29.

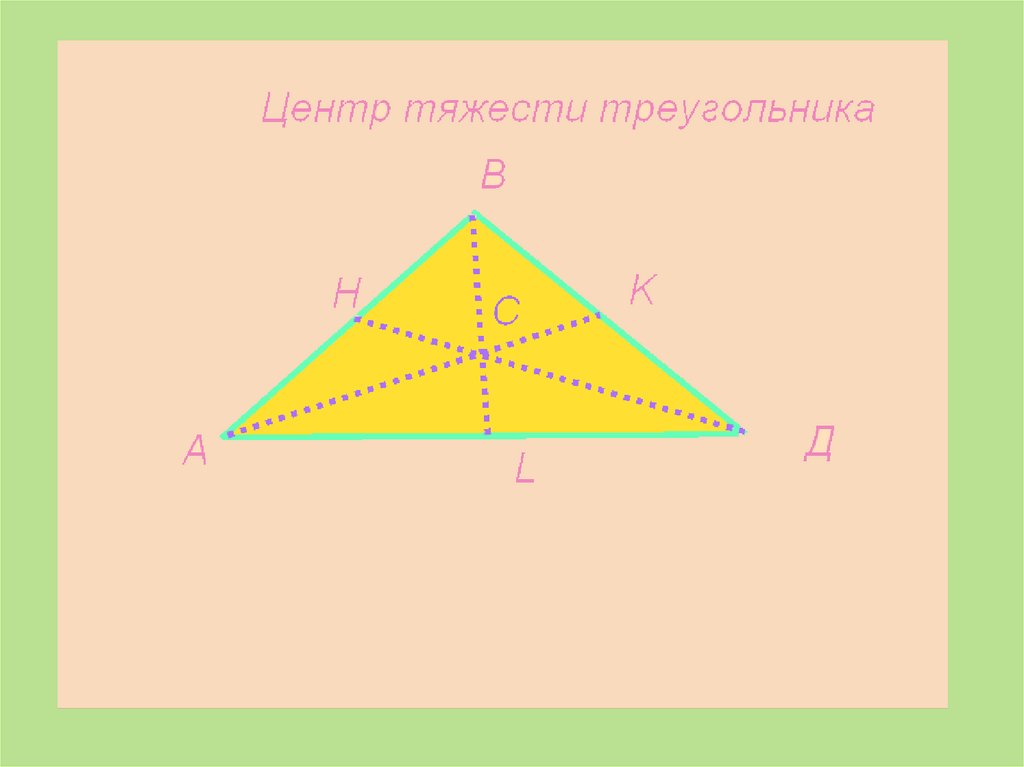
30.

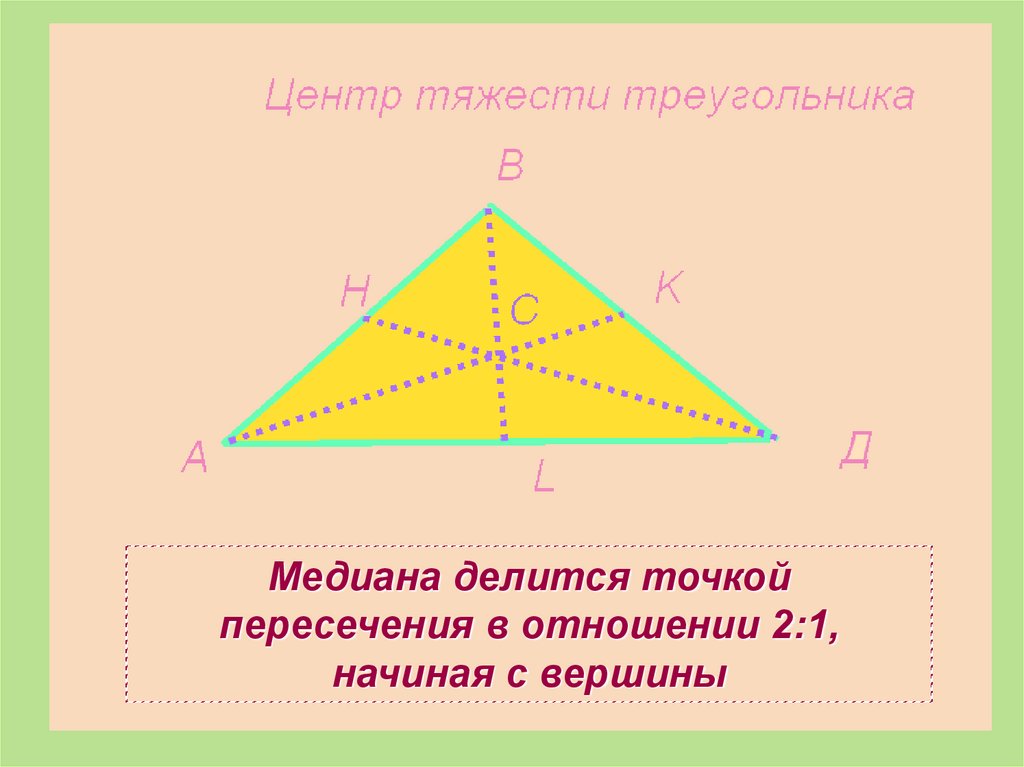
Медиана делится точкой
пересечения в отношении 2:1,
начиная с вершины

31.

32.

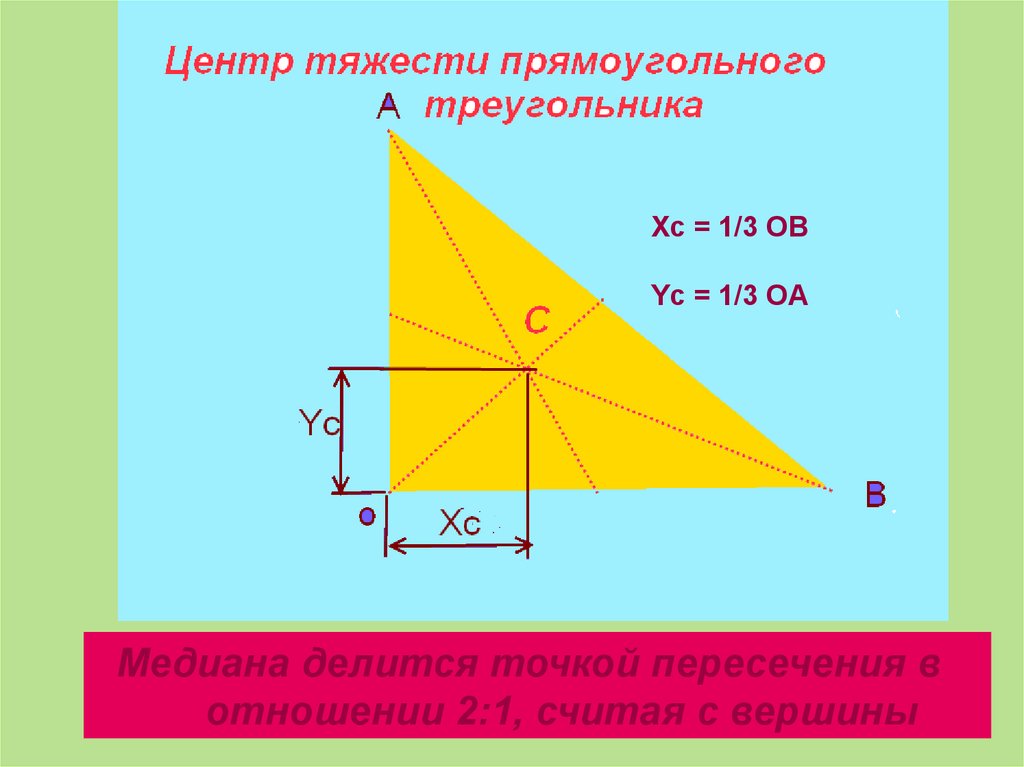
Xc = 1/3 OB
Yc = 1/3 OA
Медиана делится точкой пересечения в
отношении 2:1, считая с вершины

33.

34.

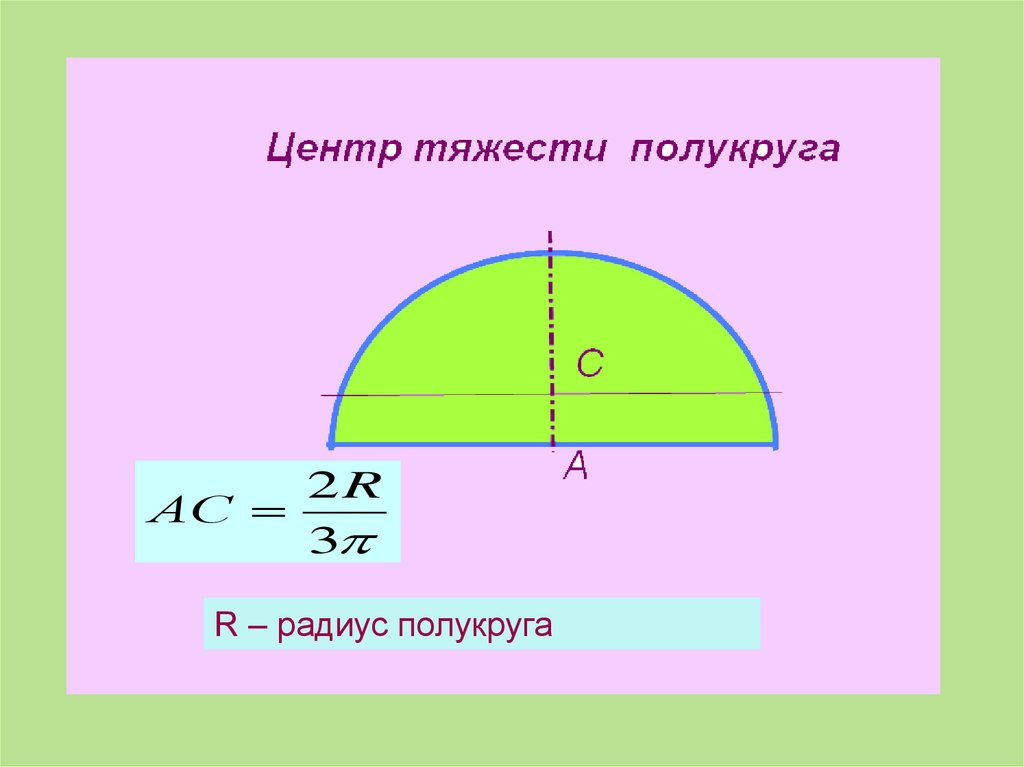
2R
АС
3
R – радиус полукруга

35. Центр тяжести кругового сектора

R – радиус
сектора;
α – угол
сектора.
2R
ОС
sin
3

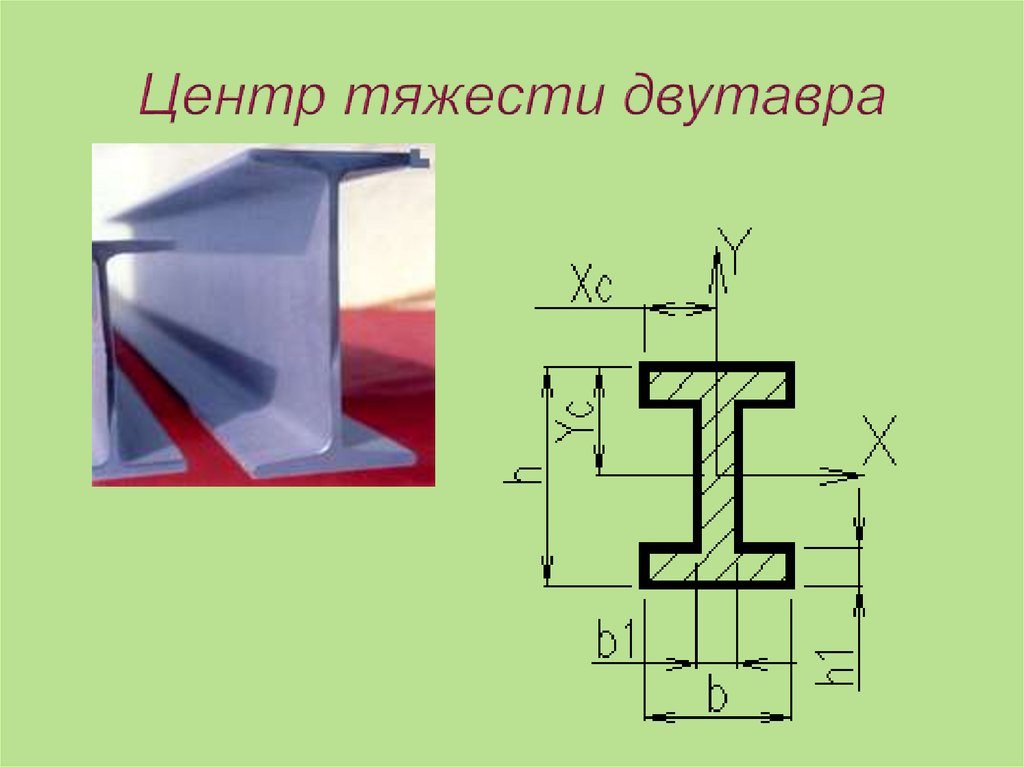
36.

37. Центр тяжести двутавра

38.

39. Центр тяжести швеллера

40.

41. Центр тяжести уголка

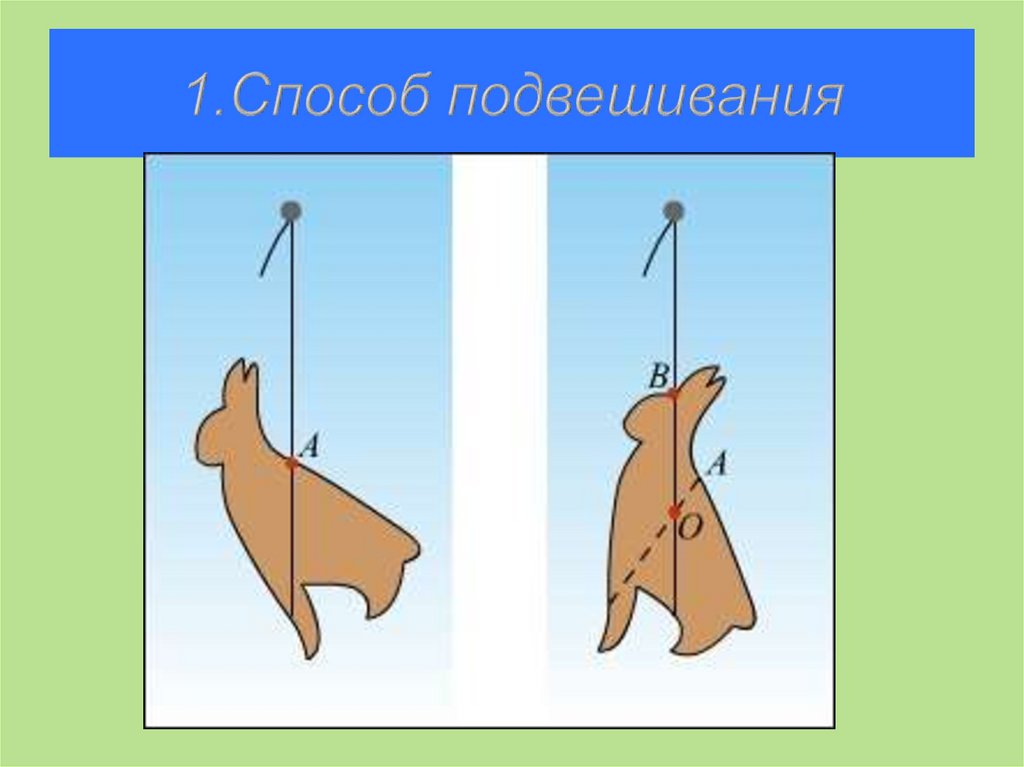
42. Определение центра тяжести фигуры неправильной формы.

1) Метод подвешивания на
острие;
2) Теоретический метод

43. 1.Способ подвешивания

44. 2. Теоретический метод

В этом случае сложная фигура разбивается
на определенное количество элементарных
фигур, имеющих правильную
геометрическую форму. Затем определяется
положение центра тяжести и площади
каждой элементарной фигуры.

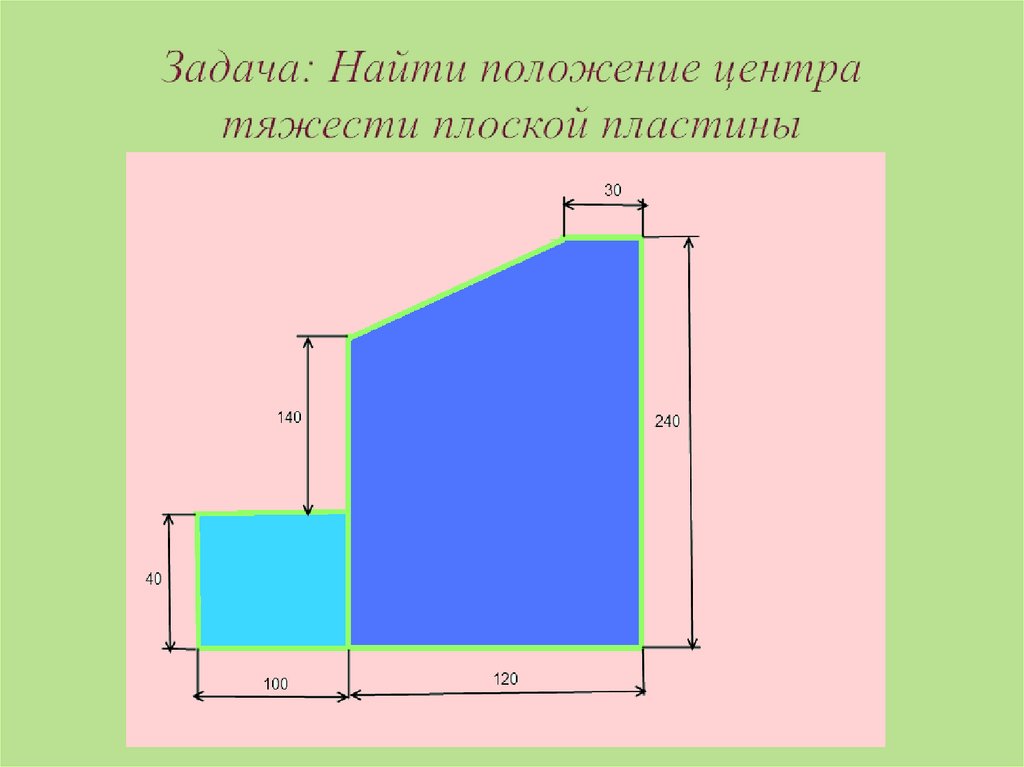
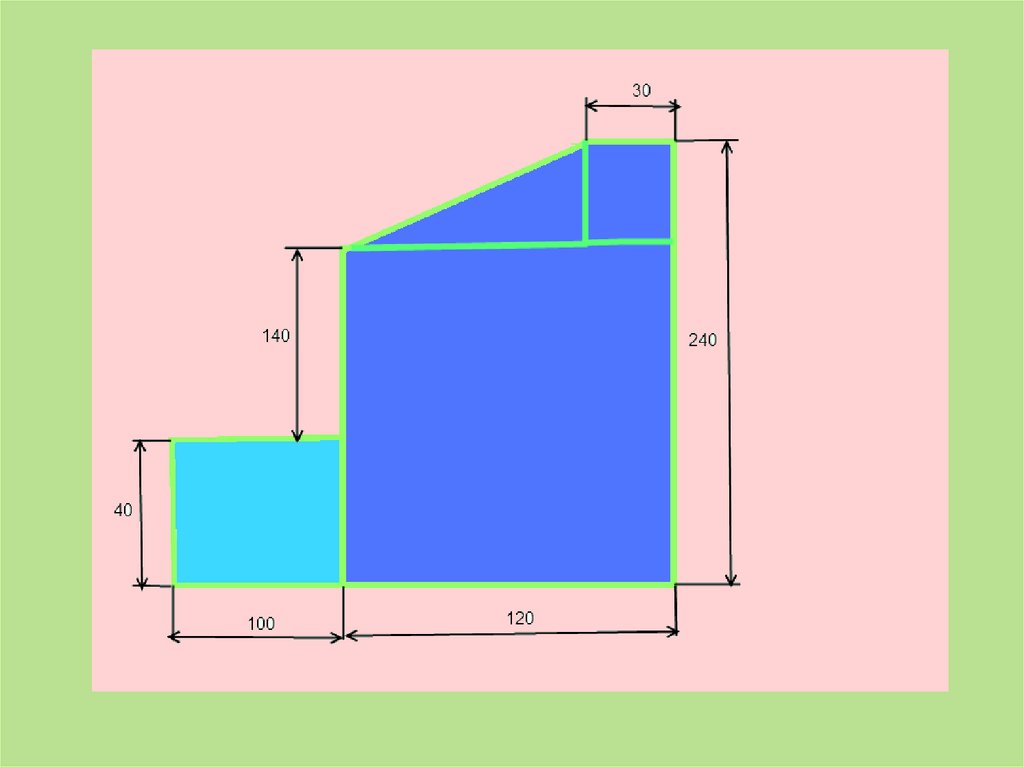
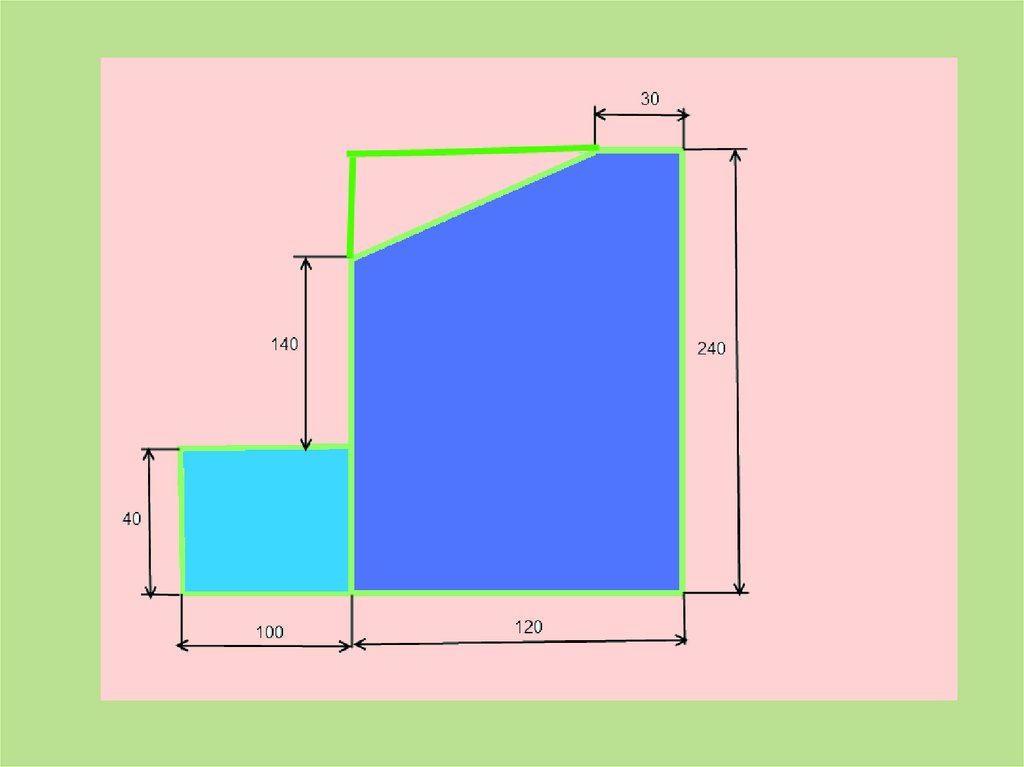
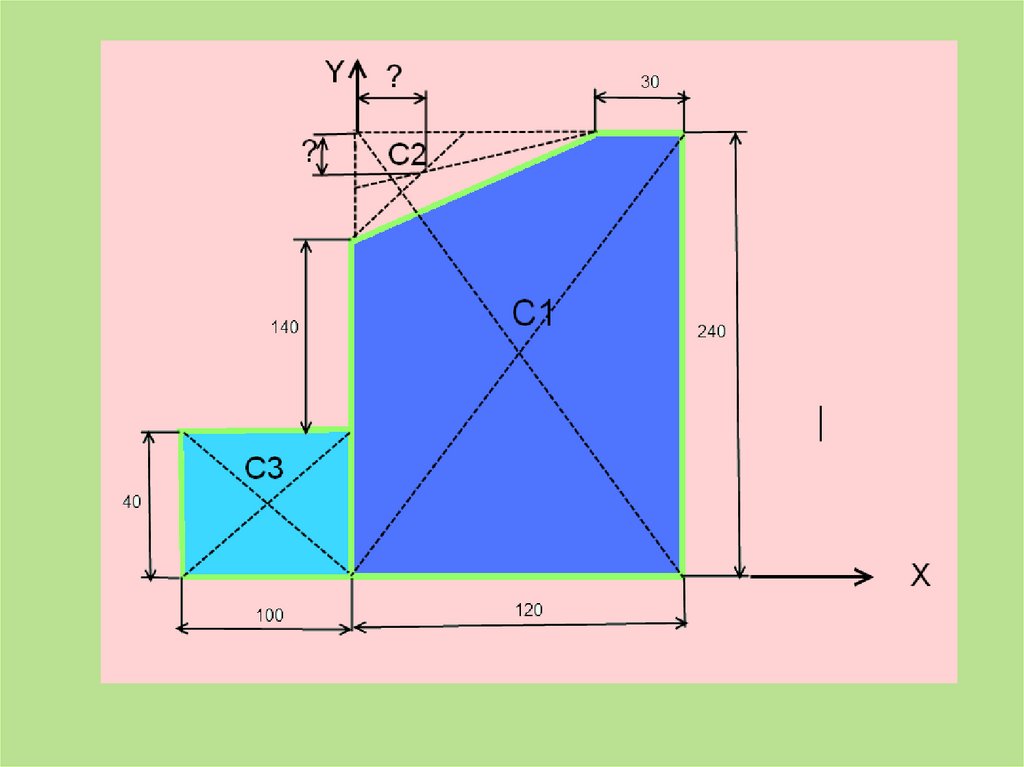
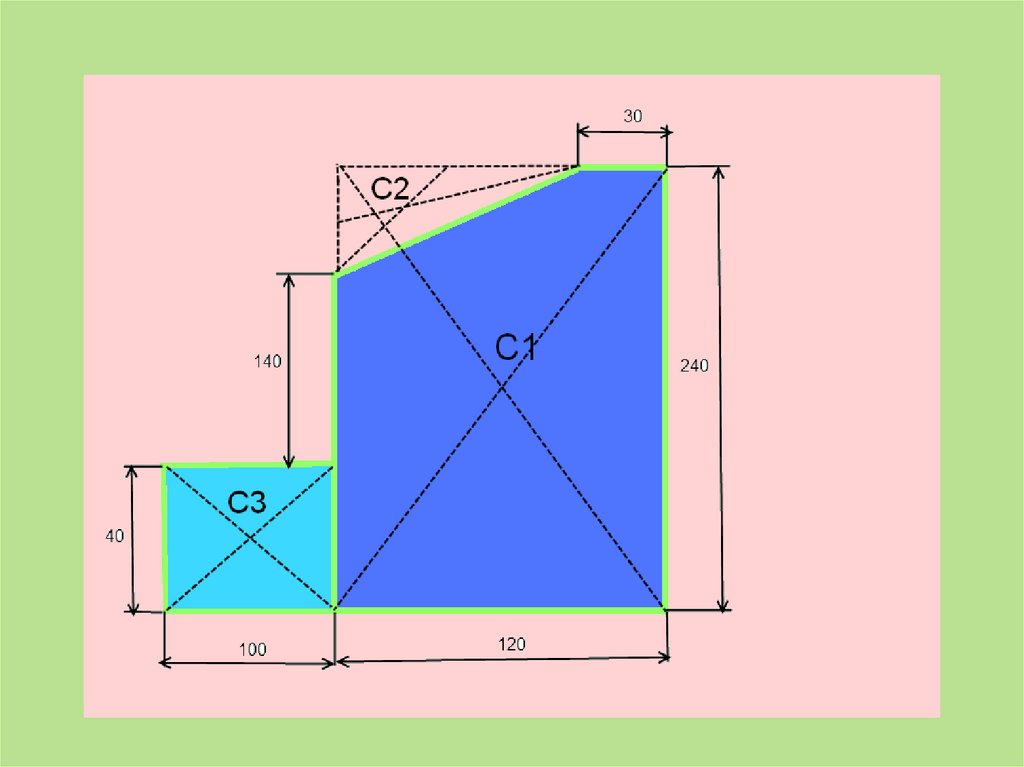
45. Задача: Найти положение центра тяжести плоской пластины

46.

47.

48.

49.

50.

51.

52.

53.

54.

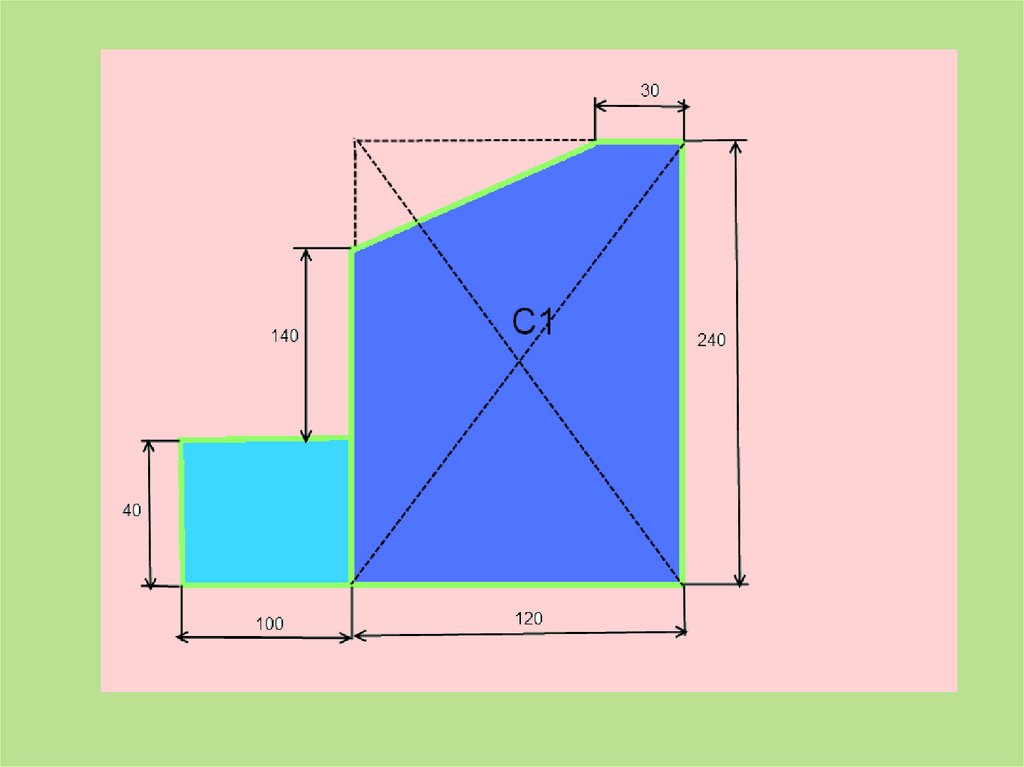
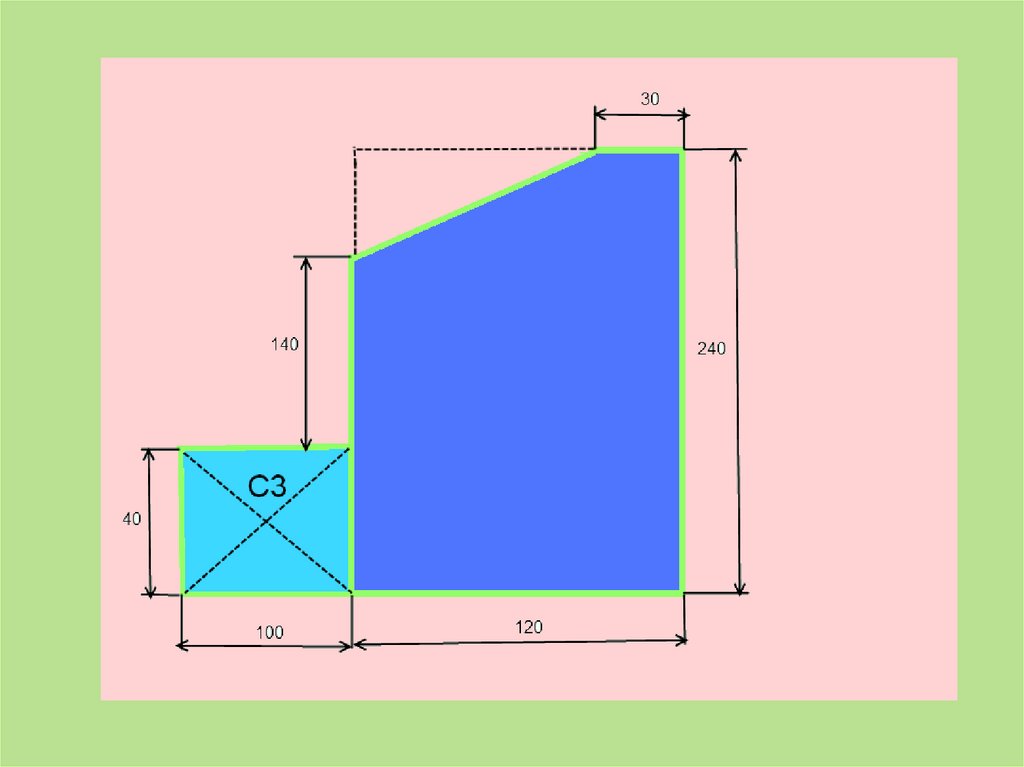
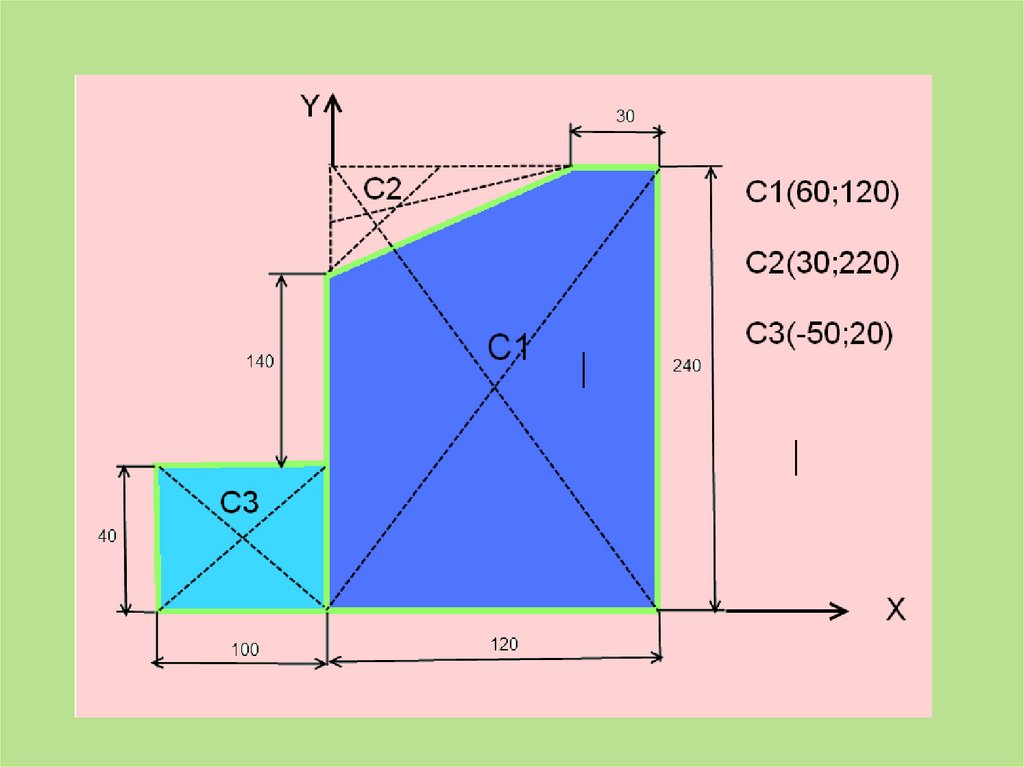
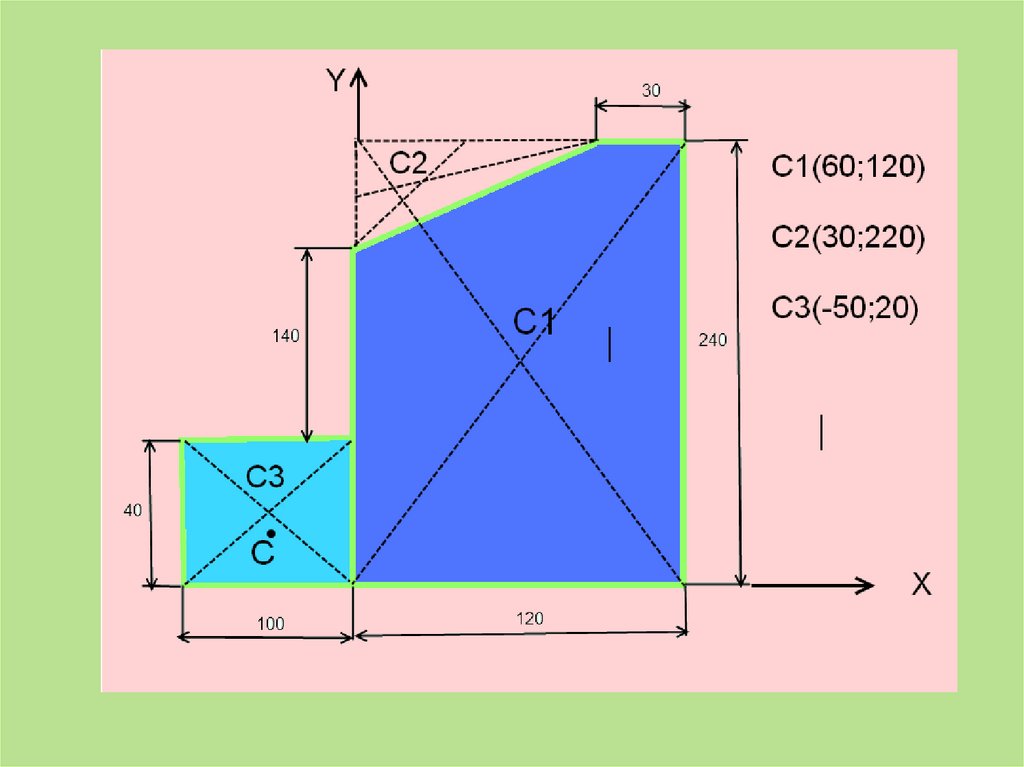
1)Прямоугольник
А1 = 10*4 = 40 см2
С1(6;12)
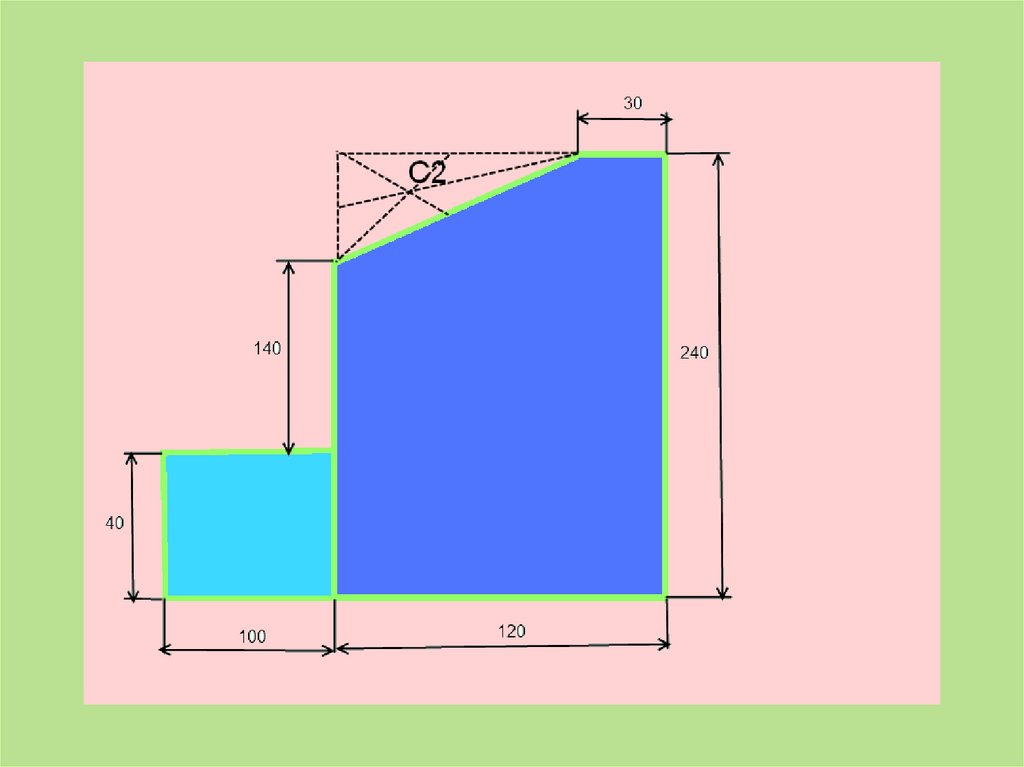
2) Прямоугольник
А2 = 12*24 = 288 см2
С2(-5;2)
n
AiXi
Хс i 1n
Ai
i 1
n
3)Треугольник
А3 = 0,5*6*9= 27 см2
С3(3;22)
AiYi
Yс i 1n
Ai
i 1

55.

1)Прямоугольник
А1 = 10*4 = 40 см2
С1(6;12)
2) Прямоугольник
А2 = 12*24 = 288 см2
С2(-5;2)
3)Треугольник
А3 = 0,5*6*9= 27 см2
С3(3;22)
n
AiXi
Хс i 1n
Ai
40 6 288 ( 5) 27 3
4,2см
40 288 27
i 1
n
Yс
AiYi
i 1
n
Ai
i 1
40 12 288 2 27 22
1,5см
40 288 27

56.

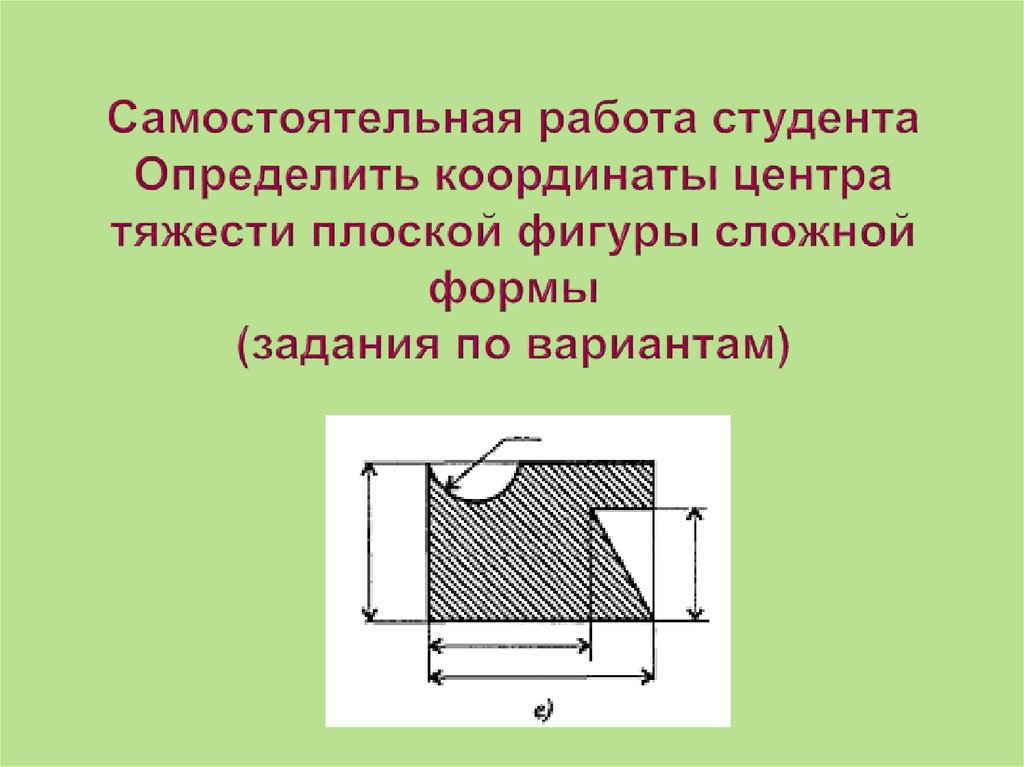
57. Самостоятельная работа студента Определить координаты центра тяжести плоской фигуры сложной формы (задания по вариантам)

58.

Задание на дом
СРС : Определить координаты
центра тяжести плоской фигуры
Фигуру начертить произвольных
размеров (не менее четверти
тетрадного листа), проставить
необходимые размеры.