Акимутин.ppt 1

1. Свойство точек параллельных прямых.

Выполнил студент 5 курса 5 группы ФМФ
Акимутин Александр.
Научный руководитель: профессор кафедры
методики обучения математике и
информационных технологий
Брянского госуниверситета, доктор педагогических наук
Малова Ирина Евгеньевна.
2009 г.

2.

Справедливо утверждение: все точки плоскости, расположенные по одну
сторону от данной прямой и равноудаленные от нее, лежат на прямой,
параллельной данной (выполите рисунок). На этом свойстве основано
устройство инструмента, называемого рейсмусом (рис.а)
Рейсмус используется в столярном деле для разметки на поверхности
деревянного бруска прямой, параллельной краю бруска. При передвижении
рейсмуса вдоль края бруска металлическая игла прочерчивает отрезок прямой,
параллельный краю бруска. (рис. б).
Сформулируйте утверждение, обратное рассмотренному.
Все точки каждой из двух параллельных прямых равноудалены от другой
прямой.
Докажем это утверждение.

3.

Теорема: Все точки каждой из двух параллельных прямых равноудалены от
другой прямой.
Дано:
a║b;
a
A a, C a;
A
C
AB ┴ b, CD ┴ b.
D b, B b
Доказать:
AB = CD.
b
О каких фигурах идёт речь в теореме?
О двух параллельных прямых.
B
D
Что требуется доказать?
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
Когда говорится о всех точках, а все проверить невозможно, то на одной прямой
выбирают произвольно некоторую точку и доказывают, что расстояние от любой
другой точки этой прямой до другой прямой будет таким же, как о первой выбранной
точки. Итак, Сколько достаточно взять точек одной прямой, чтобы показать, что все
точки каждой из двух параллельных прямых равноудалены от другой прямой?
Достаточно выбрать две произвольные точки.
Важно, на какой прямой выбраны эти точки?
Нет.
Выберем на прямой а две точки. Как показать расстояния от этих точек до прямой?
Надо из выбранных точек опустить перпендикуляры на другую прямую.

4.

Теорема: Все точки каждой из двух параллельных прямых равноудалены
от другой прямой.
a
A
C
Дано:
a║b;
A a, C a;
AB ┴ b, CD ┴ b.
D b, B b
Доказать: Поиск способа доказательства
B
AB = CD.
Как обычно доказывают равенство отрезков?
b
D
Через равенство треугольников.
Какое дополнительное построение нужно провести, чтобы образовались
треугольники? Соединить точки А и D.
Какой вид треугольников ABD и DCA.
Они прямоугольные. Почему?
В = 90 (по условию),
СD b (по условию), а || b (по условию), значит, СD a (если одна из
параллельных прямых перпендикулярна третьей, то и вторая прямая ей
перпендикулярна.), значит, С = 90 .
Что делают дальше после определения вида треугольников для доказательства их
Находят пары нужных элементов.
равенства?
Сколько пар нужных элементов нужно найти и почему
2 пары, так как треугольники прямоугольные.

5.

A
C
Какие это элементы?
ADB= CAD как накрест лежащие углы при
пересечении двух параллельных прямых секущей,
АВ – общая.
b
B
Какой вывод можно будет сделать о ABD и DCA?
Они равны по гипотенузе и острому углу.
Какой вывод из равенства треугольников нам нужен?
AB=CD.
a
D

6.

Теорема: Все точки каждой из двух параллельных прямых равноудалены
от другой прямой.
Изучите доказательство, предложенное в учебнике.
A
X
a
Выделите этапы доказательства.
1
1. Доказывают, что Х = 90 .
2. Доказывают, что треугольники равны.
3. Делают выводы.
2
B
b
Y
Доказательство:
Рассмотрим параллельные прямые a и b. Отметим на прямой a точку А
и проведём из этой точки перпендикуляр АВ к прямой b. Докажем, что
расстояние от любой точки X прямой a до прямой b равно AB.
Проведём из точки X перпендикуляр XY к прямой b.1.Так как XY ┴ b, то XY ┴ a,
2.Прямоугольные треугольники ABY и YXA равны по гипотенузе и острому углу
(AY – общая гипотенуза, 1 = 2 как накрест лежащие углы при пересечении
параллельных прямых а и b секущей AY). 3. Следовательно, XY = AB. Итак,
любая точка X прямой а находится на расстоянии АВ от прямой b. Очевидно, все
точки прямой b находятся на таком же расстоянии от прямой а.
Теорема доказана.
Какой шаг пропущен?
Дополнительное построение.

7.

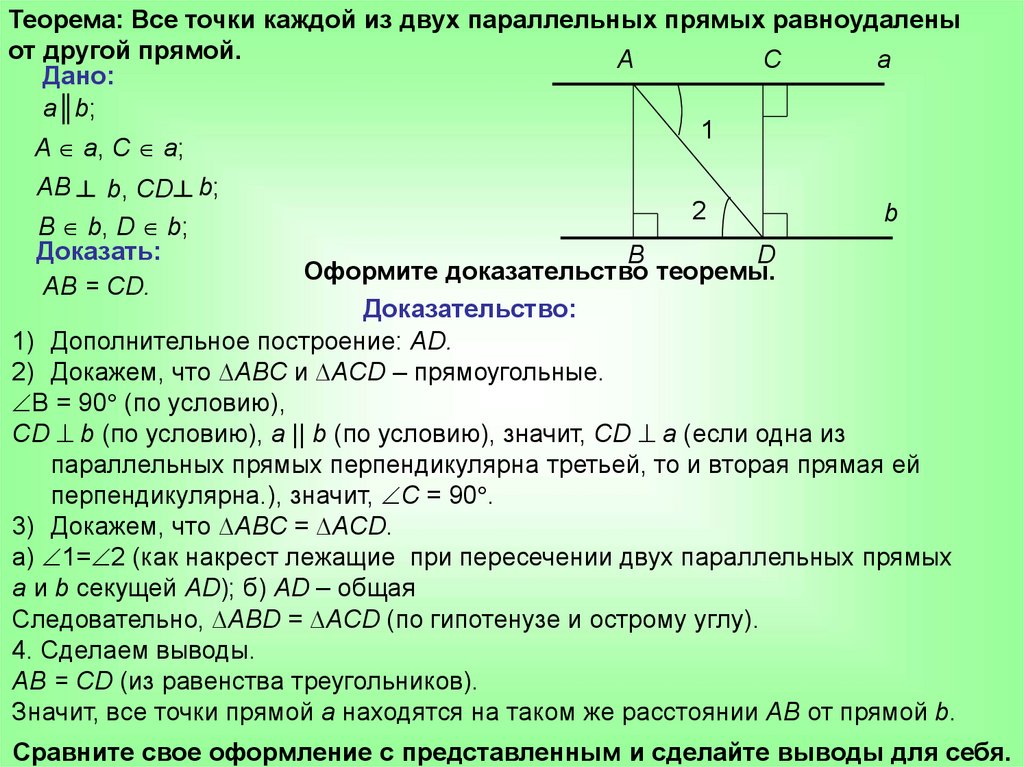
Теорема: Все точки каждой из двух параллельных прямых равноудалены
от другой прямой.
A
С
a
Дано:
a║b;
1
A a, С a;
AB ┴ b, CD ┴ b;
2
b
В b, D b;
Доказать:
B
D
Оформите доказательство теоремы.
AB = СD.
Доказательство:
1) Дополнительное построение: АD.
2) Докажем, что ∆ABС и ∆AСD – прямоугольные.
В = 90 (по условию),
СD b (по условию), а || b (по условию), значит, СD a (если одна из
параллельных прямых перпендикулярна третьей, то и вторая прямая ей
перпендикулярна.), значит, С = 90 .
3) Докажем, что ∆ABС = ∆AСD.
а) 1= 2 (как накрест лежащие при пересечении двух параллельных прямых
а и b секущей AD); б) АD – общая
Следовательно, ∆ABD = ∆ACD (по гипотенузе и острому углу).
4. Сделаем выводы.
AB = СD (из равенства треугольников).
Значит, все точки прямой а находятся на таком же расстоянии АВ от прямой b.
Сравните свое оформление с представленным и сделайте выводы для себя.

8.

Подведём итоги работы с теоремой.
С каким фактом познакомились?
Все точки каждой из двух параллельных прямых равноудалены
от другой прямой.
Взаимное расположение каких фигур данный факт характеризует?
Двух параллельных прямых.
Можно ли назвать данную теорему свойством параллельности прямых?
Да, так как в условии теоремы сказано о параллельных прямых.
Как мы переформулировали слова «все точки прямой а находятся на
одинаковом расстоянии от прямой b», чтобы доказать теорему?
Мы доказали, все точки прямой а находятся на таком же расстоянии АВ от
прямой b, где точка А была выбрана произвольно на прямой а.