Похожие презентации:
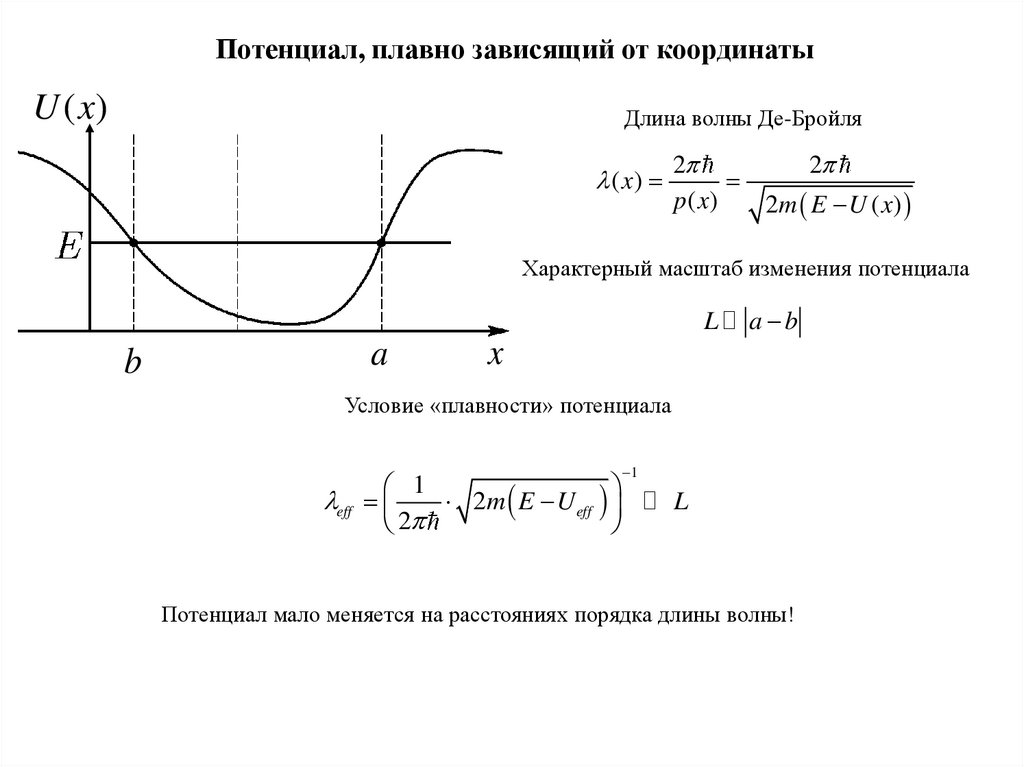
Потенциал, плавно зависящий от координаты
1.
Потенциал, плавно зависящий от координатыU ( x)
Длина волны Де-Бройля
( x)
2
2
p ( x)
2m E U ( x )
Характерный масштаб изменения потенциала
L
b
a
a b
x
Условие «плавности» потенциала
1
eff
2m E U eff
2
1
L
Потенциал мало меняется на расстояниях порядка длины волны!
2.
Потенциал, плавно зависящий от координатыx
U ( x)
Рассмотрим интервал
x
L
Длина волны практически постоянна на интервале x
( x)
b
a
x
2
2
p ( x)
2m E U ( x )
Число длин волн, «укладывающихся» в интервал
n( x)
x
x
( x)
Число длин волн, «укладывающихся» на всю траекторию
dx
n( x) n ( x)
Переписать условие квантования через импульс?
3.
Правило квантования Бора-Зоммерфельдаdx
p( x)dx
( x) 2 n
p( x)dx 2 n
Физический смысл интеграла в левой части правила квантования
Пример: глубокая прямоугольная яма
Площадь, «заметаемая» фазовой траектории
p
S p ( x)dx
Sn
0
S 2
x
a
Минимальный фазовый объём,
отвечающий состоянию частицы
в трёхмерном пространстве с
заданными импульсом и координатой
(2 )3
Число состояний в фазовом объёме Vphase
N
V phase
(2 )3
4.
Возможные значения энергии гармонического осциллятораПравило квантования
m 2 x 2
U ( x)
2
p( x)dx 2 n
Связь энергии и импульса
p ( x ) 2m E U ( x )
a
a x
Найти возможные значения энергии?
5.
Промежуточные формулыa
1
m 2 x 2
m 2 x 2
2E
2
2 dx 2m E
4
2
mE
dx
1
4
2
mE
d
1
2
2
2
E
m
a
0
0
a
Возможные значения энергии
En n
Предел больших квантовых чисел
En 1 En
1
En
n
n 1
Согласно принципу соответствия, дискретность исчезает!
6.
ЗадачаДля ультрахолодных нейтронов найти связь энергии частиц с максимальной высотой
подъёма в гравитационном поле Земли.
Ультрахолодные нейтроны, очень медленные нейтроны, со скоростями порядка 5 м/сек.
Термин «У. н.» объясняется тем, что примерно с такой же скоростью двигались бы
молекулы газа при температуре ниже 0.02 K. У. н. обладают малой кинетической энергией
(порядка 10-7 эв), недостаточной для преодоления слабого отталкивания ядрами большинства
химических элементов, и поэтому полностью отражаются от поверхности многих материалов.
7.
Рис. 1. Схема эксперимента по наблюдению квантовых уровней энергии нейтронов вгравитационном поле Земли. Ультрахолодные нейтроны влетают в узкий зазор между
плитой и поглотителем и, подпрыгнув несколько раз, долетают до счетчика нейтронов.
Если высота прыжков составляет доли миллиметра, эти прыжки описываются уже не
классической, а квантовой физикой. Измеряя поток нейтронов в зависимости от ширины
зазора, можно обнаружить квантование нейтронного движения по вертикали. Схема из
статьи Thomas J. Bowles, 2002. Quantum physics: Quantum effects of gravity
8.
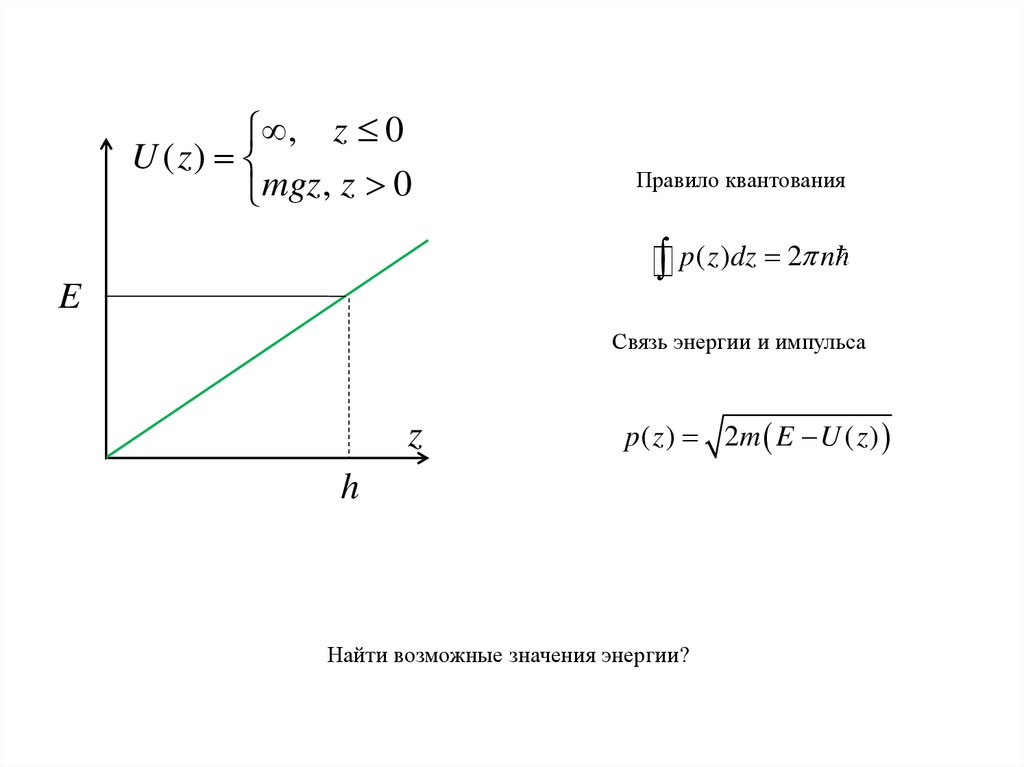
, z 0U ( z)
mgz, z 0
Правило квантования
p( z )dz 2 n
E
Связь энергии и импульса
z
p ( z ) 2m E U ( z )
h
Найти возможные значения энергии?
9.
Промежуточные формулыh
h
1
mgz
E
2 dz 2m E mgz 2 2mE dz 1
2 2mE
d 1
E
mg 0
0
0
Возможные значения энергии
En
3
2
2/3
mg
2
n
2 1/ 3
2/3
Максимальная высота при заданной энергии
hn max
En 3
g
2
2/3
1/ 3
m
2/3
n
g
2







 Физика
Физика








