(9.1) 3 îѽ¬á∩ »α∩¼«πú«½∞¡á∩ ∩¼á (2)

1.

«Мелкая» прямоугольная яма
Рассматриваем случай финитного движения (в классической механике)
a
I
En ?
E E 0
0, | x | a
U ( x)
U 0 ,| x | a
Уравнение Шрёдингера
a
II
III x
U0
pˆ 2
2m U x x E x
Уравнение Шрёдингера в разных областях
I , III : k 0, k
2
II :
2 0,
2m E
2
2m
2
U E
0

2.

В «мелкой» яме существует только одно чётное решение
I , III : A e k|x|
II : B cos x
Условия сшивки
A e ka B cos a 0
ka
kA e B sin a 0
Уравнение для энергии
k
tan a
Уравнение для энергии и безразмерных переменных
2mU 0 a 2
1 tan ; a,
2
2
Найти решение в приближении «мелкой» ямы
2mU 0 a 2
2
1

3.

1
2
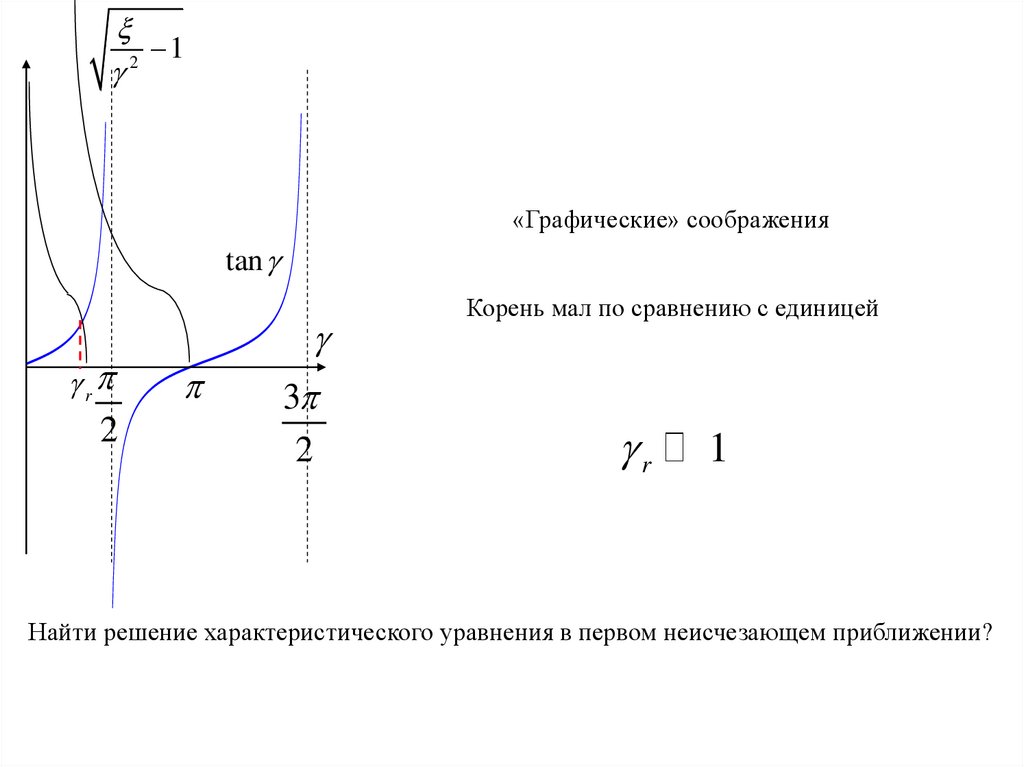
«Графические» соображения
tan
r
2
3
2
Корень мал по сравнению с единицей
r
1
Найти решение характеристического уравнения в первом неисчезающем приближении?

4.

Решение
1 tan
2
4 2 0
Или
2
1
2
1 4 1
Найти энергию в первом неисчезающем приближении при
1

5.

Решение с точностью до линейного слагаемого
2
1
2
1 4 1
Или, возвращаясь к исходным обозначениям
2ma 2
2
U E
0
2mU 0 a 2
2
E 0
Является ли ответ физически значимым?
Указание: подставить полученное значение в условия сшивки.

6.

Условия сшивки при нулевой энергии
A B cos 0
B sin 0
A B 0 x 0
Надо искать решение с точностью до квадратичных слагаемых
2

7.

Решение с точностью до квадратичных слагаемых
Полезная формула
x x2
1 x 1
2 8
Поэтому
2
1
2
1 4 1
2
Или
2ma
2
2
U E
0
2mU 0 a
2
2
2mU 0 a
2
2
2
E
2mU 0 a 2
2
U0 U0
Энергия связанного состояния в мелкой яме много меньше глубины ямы!
U0

8.

В том же приближении найти волновую функцию связанного состояния?
Указание. Оценить величины
ka ?, a ?
и записать условия сшивки для «мелкой» ямы.

9.

Неравенства для «мелкой» ямы
ka
2m E a 2
2
1, a
1 e ka cos a 1
Условия сшивки для «мелкой ямы
A B
Волновая функция частицы в «мелкой» яме во всём интервале изменения координаты
I , II , III : x A e
k | x|
Вычислить нормировочную константу?

10.

Волновая функция частицы в «мелкой» яме во всём интервале изменения координаты
x k e
k|x|
, x ] , [
Задачи.
1. Вычислить средние значения кинетической и потенциальной энергии частицы в
мелкой яме.
2. Найти плотность распределения вероятности для импульса частицы в
мелкой яме.

11.

1. Вычислить средние значения кинетической и потенциальной энергии частицы в
мелкой яме.
Среднее значение кинетической энергии частицы в мелкой яме.
2 k | x|
1
k
d
e
2
k | x|
T
dx x pˆ x
dx e
2
2m
2m
dx
2
d 2 e k|x|
?
2
dx

12.

Из семинара о дельта-функции
d e k|x|
d | x|
k e k|x|
k e k|x| ( x) ( x)
dx
dx
d 2 e k|x|
d k|x|
d e k|x|
| x|
k
e
(
x
)
(
x
)
k
(
x
)
(
x
)
2
k
e
( x)
2
dx
dx
dx
2
k | x|
d e
dx 2
k 2 e k|x| 2k ( x)

13.

Среднее значение кинетической энергии частицы в мелкой яме (продолжение)
2 3
2 2
1
k
k
2
2 k | x|
T
dx x pˆ x
dx e
dx ( x)
2m
2m
m
Вычислить интегралы?

14.

Интегралы
2
3
2
2
2 2
k
k
k
2 k | x|
dx e
d e
2m
2m 0
2m
2
2 2
k2
k
dx ( x)
m
m
Среднее значение кинетической энергии частицы в мелкой яме (продолжение)
2
2
k
T
2m

15.

Среднее значение потенциальной энергии частицы в мелкой яме.
a
a
U dx x U x x kU 0 dx e 2 k|x| 2kaU 0
Сравнить величины средних значений кинетической и потенциальной энергий?

16.

Отношение средних значений кинетической и потенциальной энергий
2
2
2
2
T
k
1
U
2m 2kaU 0
ka ,
k
| E | U 0
2m
U 0 1
T
U 2 U 0 2

17.

Найти плотность распределения вероятности для импульса частицы в
мелкой яме.
Используя принцип суперпозиции, записать в явном виде волновую функцию
в импульсном представлении?

18.

Волновая функция в импульсном представлении
( x) dp a p p ( x), a p dx p ( x) ( x)
Связанное состояние в «мелкой» яме
ap
k
2
dx e k|x| ipx / ?

19.

Результат
ap
k
2
3/ 2
dx e k|x| ipx /
k
2 k
kx ipx /
kx ipx /
dx e
dx e
2
2
2 0
p
k
0
Плотность распределения вероятности импульса
k
2
p
2
p 2 k 2
3
Оценить дисперсию импульса и координаты?