Прямоугольная яма

1.

Найти возможные значения энергии в прямоугольной яме конечной глубины
Рассматриваем случай финитного движения (в классической механике)
a
I
En ?
E E 0
0, | x | a
U ( x)
U 0 ,| x | a
Уравнение Шрёдингера
a
II
III x
U0
pˆ 2
U x x E x
2m
Уравнение Шрёдингера в разных областях
I , III : k 0, k
2
II :
2 0,
2m E
2
2m
2
U
0
E

2.

Схема решения в общем случае
Волновая функция в разных областях
I : C1 e kx C2 e kx
II : B1 cos x B2 sin x
III : A1 e kx A2 e kx
Как определить неизвестные коэффициенты?

3.

Неизвестные коэффициенты можно найти из граничных условий на бесконечности
x 0
и условий сшивки в точках скачка потенциала!
Условия сшивки в точках скачка потенциала
2 d 2 x
a dx 2m dx 2 U x E x 0
0
a
Вычислить предел?

4.

Условия сшивки в точках скачка потенциала
2
d 2 x
dx
a 0 a 0
2
2m a dx
2m
0
2 a
a
dx U x E x
a
0
0
Условия сшивки в точках скачка потенциала
a 0 a 0 0

5.

Схема решения в общем случае
Волновая функция в разных областях
I : C1 e kx C2 e kx
II : B1 cos x B2 sin x
III : A1 e kx A2 e kx
Граничные условия и условия сшивки
x 0
a 0 a 0 0
a 0 a 0 0

6.

Из граничных условий
I : C e kx
II : B1 cos x B2 sin x
III : A e kx
Оставшиеся коэффициенты вычисляются с помощью условий сшивки.
Результативно надо решить однородную систему из четырёх уравнений!
Поступим иначе. Вычислить
Hˆ , Iˆ ?

7.

Результат
Hˆ , Iˆ 0
Собственные функции гамильтониана должны быть
собственными функциями оператора чётности!
Для собственных функций оператора чётности достаточно удовлетворить условиям сшивки
только в одной и точек разрыва потенциала!
Написать чётное решение уравнения Шрёдингера?

8.

Чётное решение
I , III : A e k|x|
II : B cos x
Записать условия сшивки в явном виде в точке a и
получить уравнение для возможных значений энергии?

9.

Условия сшивки в явном виде
A e ka B cos a 0
ka
kA e B sin a 0
Уравнение для энергии
sin a k cos a 0
Или
k
tan a
Ввести безразмерные переменные
a,
2mU 0 a 2
2
и найти графическое решение характеристического уравнения.
Указание. Записать величину ka через новые безразмерные переменные.

10.

Промежуточная формула
a
2ma 2
2
U
2 2
E
k
a
0
Или
ka 2
Характеристическое уравнение
k
ka
tan a
a
1 tan
2

11.

1
2
Характеристическое уравнение
tan
2
3
2
1 tan
2
Всегда ли существует «связанное» состояние?
«Связанное» состояние описывается затухающей
на бесконечности волновой функцией
Условие появление второго чётного уровня?

12.

«Связанное» состояние существует в прямоугольной яме любой глубины.
Даже в «мелкой» яме!
«Мелкая» яма
2mU 0 a 2
2
1
Условие появления второго чётного уровня
2mU 0 a 2
2
1
0
2
2
Написать нечётное решение уравнения Шрёдингера?

13.

Нечётное решение
I , III : A e k|x|
II : B sin x
Записать условия сшивки в явном виде в точке a и
получить уравнение для возможных значений энергии?

14.

Условия сшивки в явном виде
A e ka B sin a 0
ka
kA e B cos a 0
Уравнение для энергии
cos a k sin a 0
Или
k
cot a
Ввести безразмерные переменные
a,
2mU 0 a 2
2
и найти графическое решение характеристического уравнения.
Указание. Записать величину ka через новые безразмерные переменные.

15.

1
2
Характеристическое уравнение
cot
2
3
2
1 cot
2
Условие появления нечётного уровня?

16.

Условие появления нечётного уровня
/ 2
2
1 0
2mU 0 a 2
2
2
4
Классификация появляющихся уровней по мере увеличения глубины ямы?

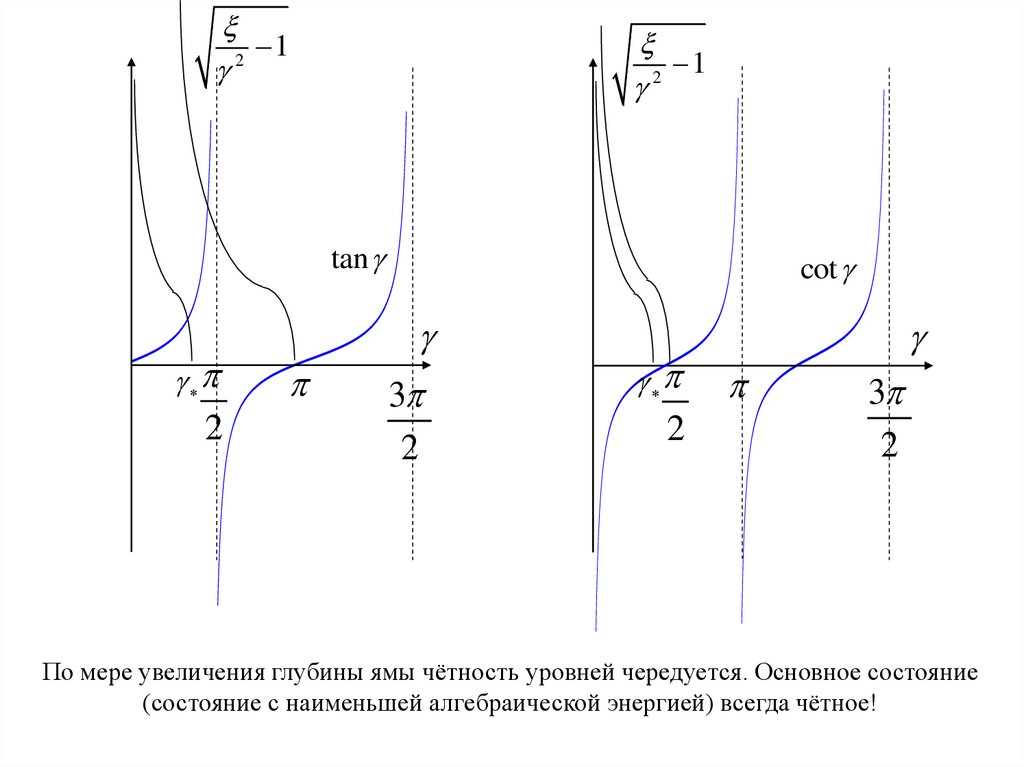
17.

1
2
1
2
tan
2
cot
3
2
2
3
2
По мере увеличения глубины ямы чётность уровней чередуется. Основное состояние
(состояние с наименьшей алгебраической энергией) всегда чётное!