Лекция 5. Многомерные случайные величины

1.

Мордовский государственный университет
им. Н.П. Огарева
Кафедра математического анализа
Лекция № 5
«МНОГОМЕРНЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ»
доцент кафедры Табачкова Марина Юрьевна
Саранск – 2014

2.

УЧЕБНЫЕ ВОПРОСЫ:
1. Многомерная случайная величина
и закон ее распределения
2. Функция и плотность распределения
двумерной случайной величины
3. Числовые характеристики
двумерной случайной величины

3. Литература

1. Кремер Н.Ш. «Теория вероятностей и математическая
статистика». Учебник для вузов. М.: ЮНИТИ-ДАНА,
2009.
2. «Математика: Математический анализ. Теория вероятностей и математическая статистика». / Под ред.
А.Н. Данчула. М.: Изд. РАГС, 2005.
3. Гельман В.Я. «Решение математических задач средствами Excel: Практикум». Учебник для вузов. СПб.:
ПИТЕР, 2003.
4. «Сборник задач по математике». М.: Изд. РАГС, 2005.

4.

ПЕРВЫЙ ВОПРОС
Многомерная случайная величина
и закон ее распределения

5.

Определение.
Случайной называется величина, которая в результате
испытания может принять то или иное значение из некоторой
совокупности своих возможных значений, причем заранее неизвестно
какое именно.
Определение.
Если результат испытания характеризуется не одной случайной
величиной, а некоторой системой случайных величин Х1, Х2, ..., Хn, то
ее называют многомерной (n - мерной) случайной величиной или
случайным вектором Х = (Х1, Х2,...,Хn).

6.

Пример.
Подбрасывают одновременнотрактовка
две игральные
кости;многомерслучайная
Теоретико-множественная
понятия
величина
X – сумма
очков, полученных в результате испытания;
ной
случайной
величины.
случайная величина Y – их произведение.
Показать, что двумерная случайная величина (Х,Y) есть функлюбаяисходов
случайная
величина
цияПоскольку
элементарных
(событий)
ω. Xi (i = 1,2,...,n) в теоретико-множественной трактовке есть функция элементарных
Решение.
событий ω, входящих в пространство элементарных событий Ω
Множество элементарных исходов (пространство элементар(ω Ω), то и многомерная случайная величина есть функция
ных событий) состоит из 36 элементарных исходов, т.е.
элементарных событий ω :
{ 1 , 2 ,..., 36} {1 / 1,1 / 2,...,1 / 6,2 / 1,2 / 2,...,2 / 6,...,6 / 1,6 / 2,...,6 / 6},
(Х1, Х2, ..., Хn) = f (ω),
где элементарный исход, например ω6=1/6, означает выпадение
т.е.
элементарному
событию ω кости
ставится
в соответствие
при каждому
подбрасывании
первой игральной
1 очка
и второй
несколько
чисел х1, х2, ..., xn, которые приняли
кости — 6действительных
очков.
Если результатом
какой-нибудь
случайные
величины Хиспытания
в результате
испытания.элемен1, Х2, ..., Хn является
тарный
исход
(событие)
ωi, хто= (х
случайные
величины X и Y полуДругими
словами
вектор
1, х2, ..., xn) называется реализачат определенные
значения;
например,
при ω6 =1 / 6 X = 7, Y= 6.
цией
случайного вектора
X = (Х
1, Х2, ..., Хn).
Совокупность этих значений (X,Y) представляет, таким образом, функцию элементарных исходов (событий) ωi.

7.

Определение.
Если результат испытания характеризуется не одной случайной
величиной, а некоторой системой случайных величин Х1, Х2, ..., Хn, то
ее называют многомерной (n - мерной) случайной величиной или
случайным вектором Х = (Х1, Х2,...,Хn).
Примеры многомерных случайных величин:
1. Успеваемость выпускника вуза характеризуется системой n случайных
величин Х1, Х2, ..., Хn — оценками по различным предметам, проставленными в
приложении к диплому.
2. Погода в данном месте в определенное время суток может быть
охарактеризована системой случайных величин: Х1 − температура; X2 − влажность; Х3 − давление; Х4 − скорость ветра и т.п.
Случайные величины Х1, Х2,...,Хn, входящие в систему, могут быть
как дискретными (пример 1), так и непрерывными (пример 2).

8.

Геометрически двумерную (X, Y) и трехмерную (X, У, Z) случайные
Наиболееможно
полным,
исчерпывающим
величины
изобразить
случайной описанием
точкой илимногомерной
случайным
случайной
ее распределения.
вектором величины
плоскостиявляется
Оху илизакон
трехмерного
пространства Oxyz, при
При
конечном
множестве
возможных
значенийсоставляющими
многомерной
этом
случайные
величины
X, Y или
Х, Y, Z являются
случайной
величины такой закон может быть задан в форме таблицы
этих векторов.
(матрицы),
всевозможные
значений
каждой из
В случаесодержащей
n-мерного пространства
(n >сочетания
3) также говорят
о случайной
одномерных
случайных
величин,
входящих
в систему,
соответствуюточке или случайном
векторе
этого
пространства,
хотя игеометрическая
щие
им вероятности.
интерпретация
в этом случае теряет свою наглядность.

9.

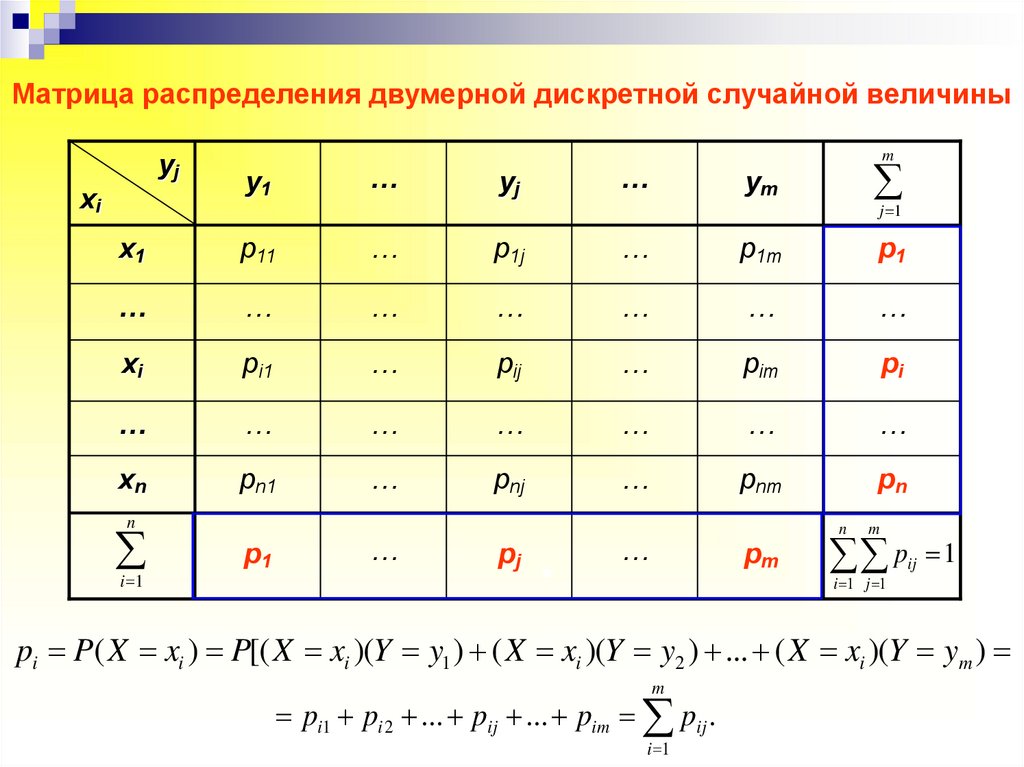
Матрица распределения двумерной дискретной случайной величины
yj
ym
…
p1m
p1
…
…
…
…
…
pij
…
pim
pi
…
…
…
…
…
…
pn1
…
pnj
…
pnm
pn
y1
…
yj
…
x1
p11
…
p1j
…
…
…
xi
pi1
…
xn
xi
m
n
i 1
p1
…
pj
.
…
j 1
n
pm
m
1.p 1
i 1 j 1
ij
pi Итоговые
P
( X xi клетке
) P[( X(ij) или
xматрицы
y1 )располагаются
таблицы
( X xi )(Yраспределения
yвероятности
ym )
столбец
строка
(X,Y)
В
каждой
произведеi )(Y
2 ) ... ( X x
i )(Y предm
ставляют
соответственно
распределения
одномерных
составляющих
ния событий
рij = P[(X = xi)(Y
= yj)].
(хi, pi) или (yj, pj). pi1 pi 2 ... pij ... pim pij .
i 1

10.

Таким образом, чтобы по таблице распределения
найти вероятность того, что одномерная случайная
величина примет определенное значение, надо просуммировать вероятности рij из соответствующей этому
значению строки (столбца) данной таблицы.

11.

Определение.
Если зафиксировать значение одного из аргументов, например,
положить Y = уj то полученное распределение случайной величины
X называется условным распределением X при условии Y = yj .
Вероятности pj (хi) или Р(хi | yj) этого распределения будут
условными вероятностями события X = xi, найденными в предположении, что событие Y = yj произошло.
Из определения условной вероятности:
p j ( xi ) P( xi | y j )
P[( X xi )(Y y j )]
P[(Y y j )]
pij
pj
.
Аналогично условное распределение случайной величины Y при
условии X = Xi задается с помощью условных вероятностей:
pi ( y j ) P( y j | xi )
P[( X xi )(Y y j )]
P[( X xi )]
pij
pi
.

12.

Пример.
Закон распределения дискретной двумерной случайной величины (X, Y) задан в таблице:
yj
-1
0
1
2
1
0,10
0,25
0,30
0,15
2
0,10
0,05
0,00
0,05
xi
Найти:
а) законы распределения одномерных случайных величин X и Y;
б) условные законы распределения случайной величины Х при
условии Y = 2 и случайной величины Y при условии X = 1;
в) вычислить P(Y < X) и P(Y ≥ X) .

13.

ВТОРОЙ ВОПРОС
Функция и плотность
распределения
двумерной случайной величины

14.

Определение.
Функцией распределения n - мерной случайной величины
(Х1, Х2, ..., Хn) называется функция F(x1, x2, ..., xn), выражающая
вероятность совместного выполнения n неравенств *:
т.е.
X1 < x1, X2 < x2, ..., Xn < xn,
F(x1, x2, ..., xn) = P(X1 < x1, X2 < x2, ..., Xn < xn).
В двумерном случае для случайной величины (X, У) функция
распределения F(x, y) определяется равенством:
F (x, y)=P(X < x,Y < y).
* Функцию F (x1, x2, ..., xn) называют также совместной функцией
распределения случайных величин Х1, Х2, ..., Хn

15.

Геометрически функция распределения
F (x,y) означает вероятность попадания
случайной точки (X,Y) в заштрихованную
область — бесконечный квадрант, лежащий левее и ниже точки М(х,у).
Правая и верхняя границы области в
квадрант не включаются — это означает,
что функция распределения непрерывна
слева по каждому из аргументов.
В случае дискретной двумерной случайной величины ее функция
распределения определяется по формуле:
В нашей лекции мыF (вx,основном
будем
вести изложение для
y)
pij ,
двумерной (n = 2) случайной величины;
при этом практически все
i
j
понятия
и утверждения,
сформулированные
для
2, которых
могут
где суммирование
вероятностей
распространяется на
всеni, =для
быть
и на случай
xi < х, иперенесены
все j, для которых
yj < у. n > 2.
Однако рассмотрение именно двумерной случайной величины
Для дискретной случайной двумерной величины (X,Y) ее функпозволяет сделать изложение наглядным и менее громоздким.
ция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции F (х, у).

16.

СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1. Функция распределения F(х,у) есть неотрицательная функция,
заключенная между нулем и единицей, т.е. 0 < F(x,y) < 1.
Утверждение следует из того, что F (х,у) есть вероятность.
2. Функция распределения F(х,у) есть неубывающая функция по
каждому из аргументов, т.е.
при х2 > х1 F(х2,у) ≥ F(x1, у), при у2 > у1 F(х, у2) ≥ F(x, y1).
Так как при увеличении какого-либо аргумента заштрихованная область на
рисунке увеличивается, то вероятность попадания в него случайной точки (X,Y),
т.е. функция распределения F (х, у), уменьшиться не может.
3. Если хотя бы один из аргументов обращается в -∞, функция
распределения F(х,у) равна нулю, т.е. F(x,-∞) = F(-∞,у) = F(-∞,-∞) = 0.
Функция распределения F (х,у) в отмеченных случаях равна нулю, так как
события Х < -∞, Y < -∞ и их произведение представляют невозможные события.

17.

СВОЙСТВА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
4. Если один из аргументов обращается в +∞, функция распределения F (х, у) становится равной функции распределения
случайной величины, соответствующей другому аргументу:
F (x, +∞) = F1 (x) и F (+∞, y ) = F2 (y)
где F1 (x) и F2 (y) − функции распределения случайных величин X
и Y, т.е. F1 (x) = P(X < x), a F2 (y) = P(Y < y).
Произведение события ( Х < х) и достоверного события ( Y < +∞) есть само
событие ( X < х), следовательно, F (x, +∞) = Р ( Х < х) = F1 (x).
Аналогично можно показать, что F (+∞, y) = F2 (y).
5. Если оба аргумента равны +∞, то функция распределения
равна единице: F(+∞,+∞) = 1.
F (+∞,+∞) = 1 следует из того, что совместное осуществление достоверных
событий ( X < +∞), ( Y < +∞) есть событие достоверное.

18.

Геометрически функция распределения есть
поверхность, обладающая указанными свойствами.
некоторая
Зная функцию распределения
F(х,у), можно найти вероятность
попадания случайной точки
(X,Y) в пределы прямоугольника
ABCD, т.е.
X x2 )( y1
Y y2 )].
P[( x1
)]
Так как эта вероятность равна вероятности попадания в бесконечный
квадрант с вершиной В(х2,y2) минус вероятности попадания в квадранты с вершинами соответственно в точках А(х1,у2) и С(х2,у1) плюс
вероятность попадания в квадрант с вершиной в точке D(x1,y1) (ибо эта
вероятность вычиталась дважды), то
P[( x1
X x2 )( y1
Y y2 )] F ( x2 , y2 ) F ( x1 , y2 ) F ( x2 , y1 ) F ( x11, y11).

19.

Определение.
Двумерная случайная величина (X,Y) называется непрерывной,
если ее функция распределения F(x,y) − непрерывная функция, дифференцируемая по каждому из аргументов, и существует вторая
смешанная производная Fxy ( x, y ).
Определение.
Плотностью вероятности (плотностью распределения или
совместной плотностью) непрерывной двумерной случайной
величины (X,У) называется вторая смешанная частная производная ее
функции распределения, т.е.
2
d F ( x, y)
f ( x, y)
Fxy ( x, y).
dxdy
f ( x, y )
Геометрически плотность вероятности
двумерной случайной величины (Х,У)
представляет собой поверхность распределения в пространстве Oxyz.

20.

СВОЙСТВА ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОЙ
СЛУЧАЙНОЙ ВЕЛИЧИНЫ
1. Плотность вероятности двумерной случайной величины есть
неотрицательная функция, т.е. f(x,y) ≥ 0.
2. Вероятность попадания непрерывной двумерной величины
(X, Y) в область D равна:
P[( X , Y ) D] f ( x, y)dxdy.
D
3. Функция распределения непрерывной двумерной случайной
Если вероятность
попадания
на отрезок
величины
может быть
выражена
через[а,b]
ееодномерной
плотность
случайной
геометрически выражается
площадью
x y
вероятностивеличины
f (x,y) по формуле:
фигуры, ограниченной сверху кривой
и . опиF ( x, распределения
y)
f (u , v)f(х)
dudv
рающейся на отрезок [а,b], то вероятность
попадания дву
мерной
случайной
величины
в область
D на плоскости
Оху
4. Двойной
несобственный
интеграл
в
бесконечных
пределах
от
Функция распределения F(x,y) есть вероятность попадагеометрически
изображается
объемом цилиндрического
тела,
плотности
вероятности
двумерной
ния в бесконечный квадрант D, который можно рассматриограниченного
сверху
поверхностью
распределения
f (х,у)
и
случайной
величины
равен
единице:
f
(
x
,
y
)
dxdy
1
.
вать
как прямоугольник,
ограниченный
абсциссами – ∞ и х , а
опирающегося
на область
D.
также ординатами — ∞ и у.

21.

Зная плотность вероятности двумерной случайной величины (X,Y), можно найти функции распределения ее одномерных составляющих Х и Y:
x
F1 ( x) f (t , y )dtdy,
y
F2 ( y ) f ( x, t ) dxdt.
Дифференцируя функции распределения F1 (x) и F2 (y) соответственно по аргументам х и у, получим плотности вероятности одномерных случайных величин Х и Y
f1 ( x ) f ( x, y ) dy ,
f 2 ( y ) f ( x, y ) dx.
т.е. несобственный интеграл в бесконечных пределах от
совместной плотности f (х,у) двумерной случайной величины
по аргументу х дает плотность вероятности f2(у), а по
аргументу у — плотность вероятности f1(x).

22.

Пример.
Двумерная случайная величина распределена равномерно
в круге радиуса R = 1.
Определить:
а) выражение совместной плотности
распределения двумерной случайной
величины (X,Y);
б) плотности вероятности одномерных
составляющих X и У;
в) вероятность того, что расстояние от
точки M(x, y) до начала координат будет меньше 1/3.
Решение.
2
2
1
при
x
y
,
а)
По
условию
в)
вероятность
того,
что
случайная
точка
будет находиться
C
б) плотности вероятности одномерных 1M(x,y)
f (1/3
x) можно
в круге
радиуса
R
=
найти
2 по
2 формуле
1
составляющих X и Y находим
по
формуле
x
y
1.
при
0
С
1/ 3
1/ 9 x 2 1
1 1 x 2 12
2
2
22 1
,Yy )dy
распределения
P X dy
Y 1 говорит,
x 2 при -1
dxdy
, 1.
Свойство
4Xf плотности
2
f1 ( x)P
(
x
≤
х
≤
1
/
3
1
/
9
x
ограниченного
3 1 x 2 поверхностью
9 расчто объем тела,
или:
2
2
пределения f (х,у)
и
плоскостью
Оху,
равен
1
.
1
1
f ( x, 2y )dx 2 1 2y 2 2 2 1
2
2
f
(
y
)
P X Y 2 2 R1 / R R1 / R при
Аналогично
-1/ 1≤ y ≤. 1.
R
C
1
,
Следовательно
и C 1 .
9
9
3

23.

Определение.
Для непрерывных
случайныхвеличин
величин
дискретных
случайных
Условным
законом
распределения одной из одномерных составляющихP[(
двумерной
величины
ее
Pf[((Xx, y(X,Y)
y j )]
X xi f)((Yx, yслучайной
)xi )(Yназывается
)y j )]
.
p j распределения,
( xi ) f y ( x) вычисленный
,и pпри
y))
i f(xy(jусловии,
закон
что ,другая составляюP[(Y f 2y(jy)])
X xi )]
f1 (Px[(
щая приняла определенное
значение (или попала
в) какой-то
интервал).
т.е. условная плотность вероятности одной из одномерных составляющих двумерной случайной величины равна отношению ее совместной плотности к плотности вероятности другой составляющей.
Данные соотношения записанные в виде f ( x, y ) f1 ( x) f x ( y ) f 2 ( y ) f y ( x)
называются теоремой умножения плотностей распределений.
Кроме того
f y ( x)
f ( x, y )
f ( x, y)dx
,
f x ( y)
f ( x, y )
f ( x, y)dy
.

24.

Определение.
Определение.
Случайные величины X и Y называются независимыми, если их
Две случайные
Х и Y называются
независимыми,
совместная
функциявеличины
распределения
F (x,y) представляется
в виде
если закон распределения
одной изF1них
от того,
произведения
функций распределений
(x) инеF2меняется
(y) этих случайных
Дифференцируя
дважды данное
равенство
по аргументам х и у,
величин,
т.е.
какие
возможные
значения
приняла
другая величина.
получим
(x,y) = F1 (x)·F
2 (y).
В противном случае Fслучайные
величины
Х и Y называются
f (x,y) = f1 (х)·f2 (у),
зависимыми.
В противном случае, при невыполнении этого равенства, случайные
т.е. для независимых
непрерывных
случайных величин X и Y их
величины
Х и Y называются
зависимыми.
совместная плотность f (x,y) равна произведению плотностей вероятности f1 (х) и f2 (у) этих случайных величин.
Таким образом (теорема умножения плотностей распределений),
независимость двух случайных величин X и Y означает, что условные
плотности вероятности каждой из них совпадают с соответствующими
«безусловными» плотностями, т.е.
fy (х) = f1 (х) и fx (у) = f2 (у).

25.

ТРЕТИЙ ВОПРОС
Числовые характеристики
двумерной случайной величины

26.

При изучении двумерных случайных величин рассматриваются
числовые характеристики одномерных составляющих X и Y —
математические ожидания и дисперсии.
Так, для непрерывной случайной величины (X,Y) они определяются
по формулам:
a x M ( X ) xf ( x, y )dxdy,
a y M (Y ) yf ( x, y )dxdy,
D( X ) ( x a x ) 2 f ( x, y )dxdy,
D(Y ) ( y a y ) 2 f ( x, y )dxdy.

27.

Наряду с ними рассматриваются также числовые характеристики
условных распределений: условные математические ожидания
Mx( Y ) и Му( Х ) и условные дисперсии Dx( Y ) и Dу( Х ).
Эти характеристики находятся по обычным формулам математического
ожидания и дисперсии, в которых вместо вероятностей событий рi и pj или
плотностей вероятности f1(х) и f2(y) используются условные вероятности pj (xi) и
pi (yj) или условные плотности вероятности fy(x) и fх(у).
Например, для непрерывной случайной величины (X,Y)
M x (Y ) y f x ( y ) dy,
Dx (Y ) [ y M x (Y )]2 f x ( y ) dy.
Условное математическое ожидание случайной величины Y при X = х,
т.е. Mx (Y), есть функция от х, называемая функцией регрессии или
просто регрессией Y по Х; аналогично Му (Х) называется функцией
регрессии или просто регрессией X по Y.
Графики этих функций называются соответственно линиями
регрессии (или кривыми регрессии) Y по Х и Х по Y.

28.

Определение.
Зависимость между переменными X и Y называется функциональной,
когда каждому значению х одной переменной соответствовало строго
определенное значение у другой.
Например, зависимость между двумя случайными величинами — числом
вышедших из строя единиц оборудования за определенный период времени и
их стоимостью — функциональная.
Определение.
Зависимость между двумя случайными величинами X и Y называется
вероятностной (стохастической или статистической), если каждому
значению одной из них соответствует определенное (условное) распределение другой.
В случае вероятностной (стохастической) зависимости нельзя, зная
значение одной из них, точно определить значение другой, а можно
указать лишь распределение другой величины.
Например, зависимости между числом отказов оборудования и затрат на
его профилактический ремонт, весом и ростом человека, затратами времени
студента на просмотр телевизионных передач и
чтение книг и т.п.
являются вероятностными (стохастическими).

29.

f x3 ( y )
f x2 ( y )
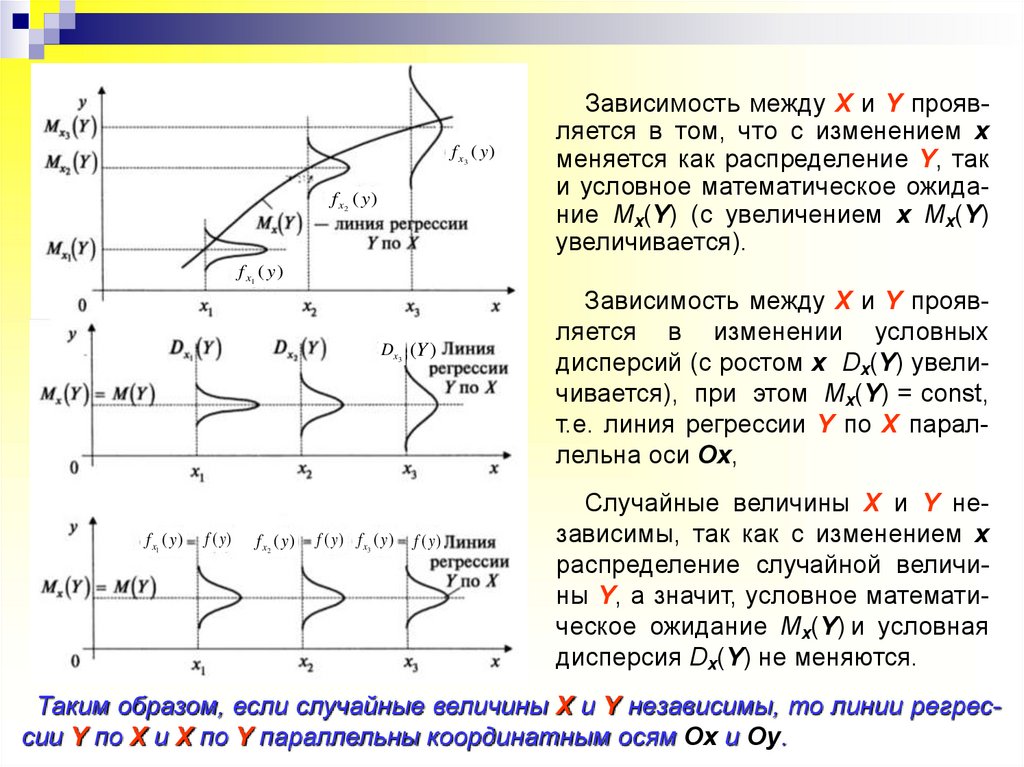
Зависимость между Х и Y проявляется в том, что с изменением х
меняется как распределение Y, так
и условное математическое ожидание Mx(Y) (с увеличением х Mx(Y)
увеличивается).
f x1 ( y )
Dx3 (Y )
f x1 ( y )
f (y )
f x2 ( y )
f (y ) f x3 ( y )
f (y )
Зависимость между Х и Y проявляется в изменении условных
дисперсий (с ростом х Dx(Y) увеличивается), при этом Mx(Y) = const,
т.е. линия регрессии Y по X параллельна оси Ох,
Случайные величины Х и Y независимы, так как с изменением х
распределение случайной величины Y, а значит, условное математическое ожидание Mx(Y) и условная
дисперсия Dx(Y) не меняются.
Таким образом, если случайные величины X и Y независимы, то линии регрессии Y по X и X по Y параллельны координатным осям Ох и Оу.

30.

Определение.
Ковариацией (или корреляционным моментом) Кху случайных
величин X и Y называется математическое ожидание произведения
Пусть имеется
двумерная
величина
(X,Y),т.е.
для коотклонений
этих величин
от своихслучайная
математических
ожиданий,
торой известно распределение,
или совместная плотность
K xy M [( X M ( X ))(Y M (Y ))],
вероятности f(х,у).
или
K xyмы
Mможем
[( X axнайти
)(Y a yматематические
)],
В этом случае
ожидания
2
2
М(Х)
M(Y)
и дисперсии D(Х) = x и D(Y) = y одномерных
где
aх==аМх,(Х),
ау = a
My(Y).
составляющих
Xи
Y.
Из определения
следует,
что Кxy = Кух. Кроме того,
Однако математические ожидания и дисперсии
случайных
K xx M [( X a x )(Y a x )] M ( X a x ) 2 D( X ),
величин X и Y недостаточно полно характеризуют двумерную
*.
т.е.
ковариация
случайной
величины
с самой
собой есть
ее дисперсия
случайную
величину
(Х,Y),
так как
не выражают
степени
зависиn
m
мости ее составляющих X и Y.
Для дискретных случайных величин K xy ( xi a x )( y j a y ) pij .
Эту роль выполняют ковариация
коэффициент
i 1 j 1 и
корреляции.
Для непрерывных случайных величин K xy ( x a x )( y a y ) f ( x, y )dxdy.
* Ковариацию называют еще вторым смешанным центральным моментом случайных величин X и Y и обозначают cov (X,Y).

31.

СВОЙСТВА КОВАРИАЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН
1. Ковариация двух независимых случайных величин равна нулю.
2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий,
т.е.
Kxy = M(XY) − M(X) · M(Y) или Кху = M(XY) − ах ·ау.
3. Ковариация двух случайных величин по абсолютной величине не
превосходит произведения их средних квадратических отклонений, т.е.
K xy x y .
2
X M ( X ) Y M (Y )
Взяв
очевидное
неравенство
K xyКовариация
M [( X M (двух
X ))(Y случайных
M (Y ))] Mвеличин
[ XYM M (характеризует
X )Y M ( Y ) X Mкак
( X )степень
M (0Y )]
изависимости
преобразовав
его, получаем:
x рассеяние yвокруг
случайных
величин, так и их
точки
M ( XY ) M ( X ) M (Y ) M (Y ) M ( X ) M ( X ) M (Y ) M ( XY ) M ( X ) M (Y ).
(ах,ау). Однако
ковариация2 K
— величина размерная, что затрудняет ее
2K
D( X )
использование.
2
x
xy
x y
D(Y )
2
y
2
xy
x y
0, откуда следует доказываемое.

32.

Определение.
Коэффициентом корреляции двух случайных величин называется
отношение их ковариации к произведению средних квадратических
отклонений этих величин:
xy corr ( X , Y )
K xy
x y
.
Из определения следует, что ρxy = ρyx = ρ. Очевидно также, что
коэффициент корреляции есть безразмерная величина.
СВОЙСТВА КОЭФФИЦИЕНТА КОРРЕЛЯЦИИ
1. Коэффициент корреляции принимает значения на отрезке [-1;1].
2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. ρ = 0.
Из независимости случайных величин следует их некоррелированность
(ρ = 0). Обратное утверждение, вообще говоря, неверно.
3. Если коэффициент корреляции двух случайных величин равен (по
абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость.

33.

НЕКОТОРЫЕ СВОЙСТВА МАТЕМАТИЧЕСКОГО ОЖИДАНИЯ И ДИСПЕРСИИ
1. Математическое ожидание произведения двух случайных величин
равно сумме произведения их математических ожиданий и ковариации
этих случайных величин:
M(XY) = M(X)·M(Y) + Kxy,
Если Кху = 0, то
M(XY) = M(X)·M(Y),
т.е. математическое ожидание произведения двух некоррелированных
случайных величин равно произведению их математических ожиданий*.
2. Дисперсия суммы двух случайных величин равна сумме их дисперсий
плюс удвоенная ковариация этих случайных величин:
D(X+Y) = D(X)+D(Y)+2Kxy.
2
Для некоррелированных
(и,
разумеется,
для
независимых)
случайных
Формула
может
быть
обобщена
на
любое
число
слагаемых
D
(
X
Y
)
M
[(
X
Y
)
(
M
(
X
)
M
(
Y
))]
* В случае
двух nсомножителей
достаточно
менее жесткого требования (чем
величин
n
n n m
n
2
2
( X M ( X−))некоррелированности
независимость)
величин.
В
случае
произ X M ( X ))(случайных
M
2
M
[(
Y
M
(
Y
))]
M
(
Y
M
(
Y
))
D числа
X i сомножителей
D( XD
X i K ij , D
( XKi ).ij – ковариация
где
X i ивеличин
Yj .
вольного
независимости
случайных
i ) 2требование
должно
быть
сохранено.
D( X ) 2 K
D(Y ).
i 1
i 1
i 1 i 1 j 1xy i 1

34.

Благодарю за
внимание,
лекция окончена!