Случайные величины

1.

2 Случайные величины
2.1 Определения и примеры
До сих пор результаты эксперимента описывались случайными событиями. Однако, очень часто, они могут быть выражены с
помощью переменных, которые в результате эксперимента со случайным исходом принимают то или иное значение и называются
случайными величинами (с.в.)
Примеры. 1. Двукратное подбрасывание монеты. С.в. - число выпавших гербов, которое является функцией элементарного
события и до проведения эксперимента неизвестно. Имеем
{ : 11,10,01,00} { : 1 , 2 , 3 , 4 }, (00) 0, (01) 1, (10) 1, (11) 2,
где 0 – соответствует цифре, 1 – гербу. Множество значений с.в. есть {0,1,2}. Интуитивно понятно, что максимальная информация,
которой мы можем располагать до проведения эксперимента, есть вероятности событий
Ai { : ( ) i, i 0,1,2} .
Т.е., вероятности
pi P( Ai ) P( ( ) i), i 0,1,2 ,
которые называются законом распределения вероятностей для данного примера.
Покажем, что зная вероятности
p( i ) P({ i }), i 1,...,4
можно найти P( Ai ) .

2.

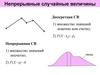
Так как
A0 { 4 } , A1 { 2 , 3 } , A2 { 1},
то
P( A0 ) p( 4 ) 1 / 4 , P( A1 ) p( 2 ) p( 3 ) 1/ 2 , P( A2 ) p( 1 ) 1 / 4 .
Возможна графическая иллюстрация.
2. Тестирование изделия до появления первого бракованного, ξ – необходимое количество тестов, характеризуется вероятностями
событий (законом распределения вероятностей)
pi P({ : ( ) i}), i 1,2,... .
3. Предположим, что на отрезок [a, b] бросается точка (рис.1). Случайная величина координата точки попадания.
Максимальная информация, которой мы можем располагать до проведения эксперимента, есть вероятности попадания точки на
всевозможные интервалы, принадлежащие отрезку
. P({ : ( ) [c, d ]}) P({ : c ( ) d }) (d c) /(b a) .
Определяют равномерный закон распределения вероятностей.
Рис.1

3.

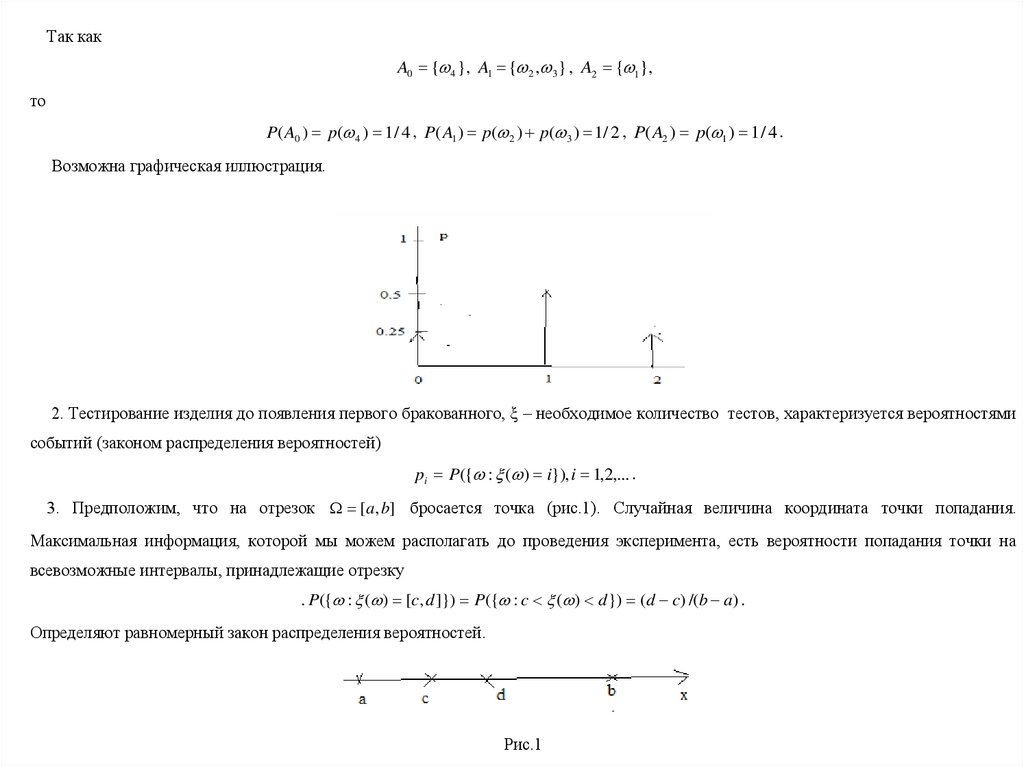
4. С.в. – диаметр заклепки. Гистограмма выборки показана на рис.2. Видно, что закон распределения вероятностей значительно
более сложный по сравнению с предыдущим примером.
Рис.2
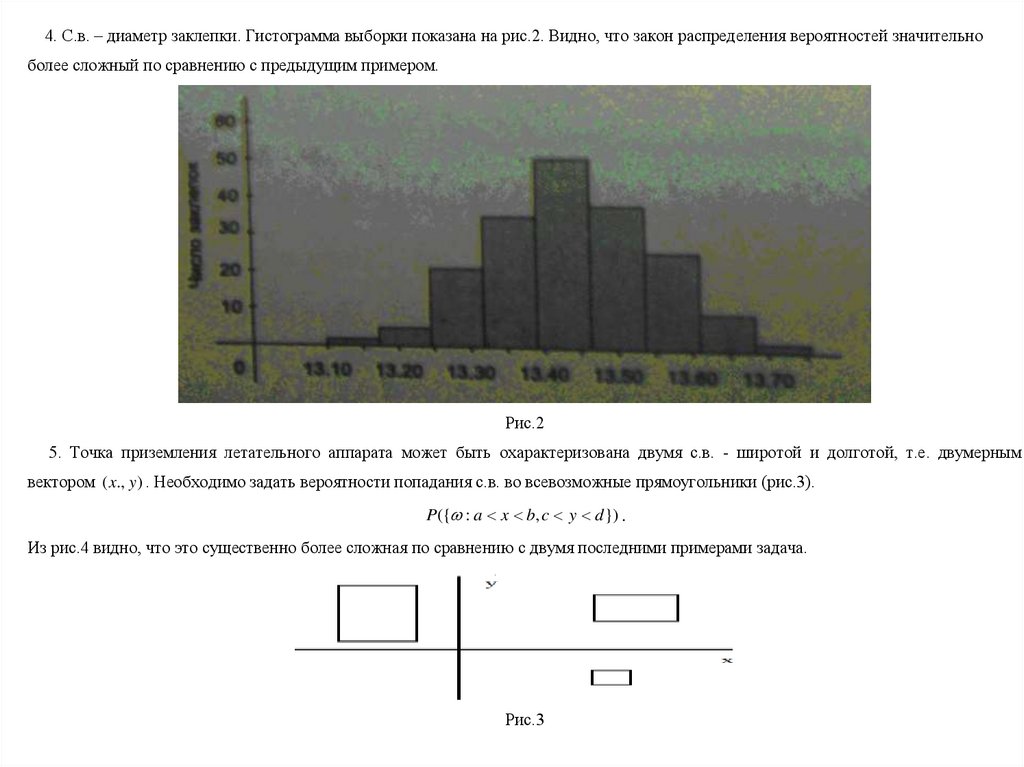
5. Точка приземления летательного аппарата может быть охарактеризована двумя с.в. - широтой и долготой, т.е. двумерным
вектором ( x., y ) . Необходимо задать вероятности попадания с.в. во всевозможные прямоугольники (рис.3).
P({ : a x b, c y d }) .
Из рис.4 видно, что это существенно более сложная по сравнению с двумя последними примерами задача.
Рис.3

4.

Рис.4
6. Стрельба по мишени. С.в. (две) – координаты точки попадания ( x, y ) . Для того, чтобы задать закон их распределения
необходимо определить вероятности попадания точки в различные области, принадлежащие мишени.
7. Измеряется дважды вес изделия. С.в. разность между результатами первого и второго измерения. Множество возможных
значений (теоретически) все точки действительной оси.
8. Время работы прибора до первой поломки.
9. Успеваемость студента, состояние любого технического устройства (например, координаты, скорость, температура и т.д.)
характеризуются векторными с.в.
Из приведенных примеров видно:
1) что с.в. бывают двух типов у одних множество значений конечно или счетно, у других оно несчетно и занимает целый участок
на действительной прямой. С.в. первого типа будем называть дискретными, а второго непрерывными.
2) максимальная информация, которой мы можем располагать о с.в. до проведения эксперимента содержится в ее законе
распределения.
Проблема: как задавать законы распределения вероятностей с.в.

5.

Итак, с.в. это переменная, которая принимает значения случайно.
Это неформальное определение. Для построения общей теории нам нужно более точное - с.в. есть функция, отображающая одно
выборочное пространство в другое - подмножество действительной оси, что можно записать так
( ) : R .
Точное математическое определение будет налагать некоторое ограничение на вид функции ( ) , чтобы теория была достаточно
содержательной, но мы принимаем, что с.в. есть просто функция.
Хотя результат эксперимента ω может быть числом, последовательностью ASCII кодов, иероглифов и т.д., значение ( ) должно
быть обязательно числом. При этом, вся случайность содержится в исходном вероятностном пространстве, а не в случайной
переменной, т.е., если ω выбрано случайно (в соответствии с заданной вероятностью), то значение с.в. будет определено однозначно.

6.

2.2 Функция распределения случайной величины
Случайная величина будет полностью определена, если задан ее закон распределения - вероятности на всевозможных множествах
представляющих интерес.
Для одномерных с.в.
pi P({ : ( ) i}), i 1,2,...
P({ : ( ) [ab]}) P({ : a ( ) b}), a, b .
Для многомерных с.в.
P({ : 1 ( ) i1 ,..., n ( ) in }), i1 ,..., in 1,2,... ,
P({ : a1 1 ( ) b1 ,..., an n ( ) bn }), a1 , b1 ,..., an , bn .
Из приведенных примеров видно, что это непростая задача. Решение определяется спецификой рассматриваемой задачи –
пространством элементарных событий и вероятностью заданной на нем. Особенно это проблематично в случае, если оно непрерывно.
Оказывается, что для того, чтобы задать закон распределения достаточно знать вероятности событий
{ : ( ) x} { : ( ) x} для любых x R ,
{ : 1 ( ) x1 ,..., n ( ) xn } { : 1 ( ) x1 ,..., n ( ) xn }, x1 ,..., xn
т.е., вероятности ее попадания не на произвольные интервалы, а только интервалы вида ( , x ) , но для любых x R одномерных с.в.
и интервалы ( , x) ... ( , x)
Определение. Функция распределения с.в. определяется выражением
F ( x) P({ : ( ) x}) P({ x}) .

7.

Определение. Функция распределения с.в. определяется выражением
F ( x) P({ : ( ) x}) P({ x}) .
Рассмотрим свойства ф.р.
1. 0 F ( x) 1 .
2. P({x1 x2 }) F ( x2 ) F ( x1 ) .
Действительно, так как { x2 } { x1} {x1 x2 } , то, используя аксиому сложения для несовместных событий
F ( x2 ) P({ x2 }) P({ x1}) P({x1 x2 }) .
Рис.1
Откуда следует свойство 2.
3.Ф.р. неубывающая функция, т.е. F ( x2 ) F ( x1 ), x2 x1 . Следует из свойства 2.
4. F ( ) lim x F ( x) 0 ,так как событие { } является невозможным.
5. F ( ) lim x F ( x) 1 ,так как событие { } является достоверным.
6.Ф.р. непрерывная слева, т.е. lim 0 F ( x ) F ( x), 0 .

8.

Найдем ф.р. для дискретной с.в., принимающей значения x1 x2 ... с вероятностями
p1 p2 ... .
Если x x1 то F ( x) 0 .
Если x1 x x2 , то событие { x} наступит тогда и только тогда, когда наступит событие { x1} . Поэтому
F ( x) P({ x}) P({ x1}) p1 .
Если x2 x x3 , то событие { x} наступит тогда и только тогда, когда наступит событие { x1} или событие { x2 } . Т.е.
{ x} { x1} { x2 } и поэтому F ( x) p1 p2 . Аналогично, если xi x xi 1 , то F ( x) p1 ... pi . Таким образом
F ( x) pi .
xi x
Рис.2
Выразим вероятности попадания с.в. на различные интервалы. Из свойства 2 следует, что
P({x1 x2}) F ( x2 ) F ( x1 ) .
Имеем
P({ x2 }) lim x2 x P({x1 x2 }) lim x2 x [ F ( x2 ) F ( x1 )] .
1
1
Если ф.р. непрерывна в точке x2 , то предел равен 0, в противном случае скачку функции в этой точке. В частности, если ф.р.
непрерывна, то вероятность, что с.в примет любое конкретное значение равно нулю. Пусть ф.р. непрерывна, тогда
P({x1 x2 }) P({x1 x2 }) F ( x2 ) F ( x1 ) .

9.

Функция распределения векторной с.в определяется выражением
F ( x1 ,..., x2 ) P({ : 1 ( ) x1 ,..., n ( ) xn }) .
Свойства многомерной ф.р. аналогичны свойствам одномерной ф.р. Сформулируем их для случая n=2.
1. 0 F ( x1 , x2 ) 1 .
2.Неубывающая функция по x1 , x2 .
3. F ( , x2 ) F ( x1 , ) F ( , ) 0 .
4. F ( , ) 1 .
5. F ( x1 , ) F1 ( x1 ), F ( , x2 ) F2 ( x2 ) .
6. P({a 1 b, c 2 d}) F (b, d ) F (a, d ) F (b, c) F (a, c) .
Докажем третье свойство. Имеем
F ( x1 , ) lim x2 F ( x1 , x2 ) lim x2 P({ 1 x1 , 2 x2 }) lim x2 P({ 1 x1} { 2 x2 }) 0 .
Докажем 5. Имеем
F ( x1 , ) lim x2 F ( x1 , x2 ) lim x2 P({ 1 x1 , 2 x2 }) lim x2 P({ 1 x1} { 2 x2 }) F1 ( x1 ) .

10.

2.3 Плотность распределения случайной величины
С.в., определенная на несчетных множествах, которая имеет дифференцируемую ф.р. называется абсолютно непрерывной. Наряду
с ф.р. для описания таких с.в. используется функция плотности распределения, определяемая выражением
f ( x) lim 0 P{ [ x, x ]} / lim 0 [ F ( x ) F ( x)] / F 1 ( x) .
Другое возможное определение
x
F ( x)
f ( x)dx .
Из определения следуют свойства п.р.
1. f ( x) 0 , так как ф.р. неубывающая функция.
2. P{ [ x, x ]} f ( x) для малых - п.р. пропорциональна вероятности того, что с.в. примет значение в окрестности точки x .
Рис.1

11.

b
3. P{ [a, b]} F (b) F (a) f ( x)dx .
a
Возможна геометрическая интерпретация вероятности попадания с.в на интервал (a, b) как площади.
Рис.2
4. P{ [ , ]}
f ( x)dx 1 .
Из определения вытекает, что вероятность того, что абсолютно непрерывная с.в. примет некоторое конкретное значение равно
нулю.

12.

Введем теперь многомерную функцию п.р. для векторной с.в. Для упрощения выкладок ограничимся двумерными с.в. В этом случае
функция п.р. определяется выражением
x1 x2
F ( x1 , x2 )
f ( x , x )dx dx
1
2
1
2
.
(1)
Полагая, что п.р. непрерывна по обоим аргументам, находим
f ( x1 , x2 ) 2 F ( x1 , x2 ) / x1 x2 .
Нетрудно получить следующие свойства многомерной п.р.
1. f ( x1 , x2 ) 0 .
b1 b2
2. P(a1 1 b1 , a2 2 b2 ) f ( x1 , x2 )dx1dx2 .
a1 a2
3.
f ( x , x )dx dx
1
2
1
2
1.
4. P{x1 1 x1 1 , x2 2 x 2 2 } f ( x1 , x2 ) 1 2 .
5. P({ 1 a, 2 b}) 0 .
6. F1 ( x1 ) F ( x1 , )
x1
f ( x1 , x2 )dx1dx2 , F2 ( x2 ) F ( , x2 )
x2
f ( x , x )dx dx
1
2
2
1
.
(2)

13.

2.4 Независимые случайные величины
Ранее мы показали, как, зная совместную ф.р. можно найти ф.р. каждой с.в. Возникает вопрос, а нельзя ли зная одномерные ф.р.
найти многомерную. Оказывается, что в общем случае нельзя и возможно только в одном частном случае, когда с.в. независимы.
С.в. ξ и η будем называть независимыми, если
F ( x1 , x2 ) F1 ( x1 ) F2 ( x2 ) .
Т.е. зная значение, которое приняла η, мы никакой новой информации о распределении ξ не получаем. Пусть ξ и η независимые с.в.
Тогда
P({a 1 b, c 2 d}) F (b, d ) F (a, d ) F (b, c) F (a, c) P({a 1 b})P({c 2 d}) .
Т.е. независимыми являются не только события попадания с.в. на полубесконечные интервалы, но и на любые другие.
Из (2) также следует, что
f ( x1 , x2 ) f1 ( x1 ) f 2 ( x2 )
для независимых с.в.
Справедлив также следующий результат. Если с.в. , независимы, то также независимы и с.в. f ( ), q( ) .
Действительно, обозначим A {x1 : f ( x1 ) x10 }, B {x2 : q( x2 ) x20 } . Имеем
F ( x10 , x20 ) P({ : x10 , x20 }) P({ : f ( ) x10 , q( ) x20 }) P({ : A, B})
P({ : A})P({ : B}) P({ : f ( ) x10 })P({ : q( ) x20 }) F ( x10 ) F ( x20 ) .

14.

2.5 Условные функции распределения
Рассмотрим две с.в. , с совместной функцией распределения F ( x, y ) . Пусть известно, что приняла значение y . Что можно
сказать при этом о распределении ?
Пример. 1.Требуется найти время пребывания покупателя в магазине, если количество человек в очереди i.
2.Стрельба по мишени. Известно, что стрелок попал в цель. Какова вероятность попадания в 10?
Начнем с самого простого случая – пусть является дискретной с.в. Тогда по определению
F ( x / y ) P({ x / y}) P({ x, y}) / P({ y})
есть условная ф.р. Можно показать, что она обладает всеми свойствами обычной ф.р. Пусть теперь н.с.в. Непосредственно
использовать это выражение мы не можем, т.к. P({ y}) 0 . Определим вначале вероятность
P({ x / y y }) P({ x, y y }) / P({ y y })
[ F ( x, y ) F ( x, y )] /[ F ( y ) F ( y )] .
Условную ф.р. определим, как предел
F ( x / y ) lim o P({ x / y y }) [ F ( x, y ) / y ] / f ( y )
x
f ( x, y)dx / f ( y) .
Используя это выражение, можно ввести условную плотность распределения
f ( x / y ) f ( x, y ) / f ( y ) .

15.

2.6 Плотность распределения функции с.в.
Пусть две с.в. связаны зависимостью g ( ) . Плотность f (x) считается известной и требуется определить f ( y ) .
Пример 1. Требуется найти мощность W RI 2 , выделяемую на нагрузке.
Пример 2. 1 и 2 - длина и ширина изделия. Требуется найти его площадь.
Будем полагать, что y g (x) монотонная функция
Пусть вначале функция монотонно возрастающая. Из рис.1 следует, что если принимает значения в интервале от x до x x , то
значения в интервале от y до y y . Поэтому вероятности этих событий совпадают
y y
x x
x
f ( z )dz
f ( z)dz .
y
Или
f ( x) x 1 ( x) f ( y ) y 1 ( y ) ,
где 1 ( x), 1 ( y) 0, x, y 0 . Откуда следует, что
f ( y) f ( x)dx / dy | x g 1 ( y ) .
Рис.1

16.

Аналогично, для монотонно убывающей функции
x x
y
x
y y
f ( z)dz f ( z)dz ,
или f ( x) x 1 ( x) f ( y ) y 1 ( y ) . Откуда находим
f ( y) f ( x)dy / dx | x g 1 ( y ) .
Рис.2

17.

2.7 Числовые характеристики случайных величин
Хотя ф.р. полностью определяет распределение с.в., часто достаточно иметь более простые (менее полные естественно)
характеристики с.в. Например, какое-то среднее вокруг которого разбросаны значения с.в. (характеристика положения), или какое-то
число, характеризующее величину этого разброса. Пользуясь такими характеристиками, мы хотим существенные особенности с.в.
охарактеризовать сжато и лаконично с помощью небольшого набора чисел, которые называются числовыми характеристиками с.в. В
ТВ такие характеристики играют огромную роль. С их помощью существенно облегчается решение многих задач. Более того, часто
удается решить задачу, не используя вообще распределение. Но можно ли охарактеризовать с.в одним или несколькими числами?
Пусть, например, с.в. есть рост взрослого человека. Хотя от наблюдения к наблюдению значения этой с.в. меняются, но существует
некоторое ее ˝среднее˝ значение – средний рост. Чтобы найти его, измерим рост n человек выбранных случайно. В результате, мы
получим n значений x1 ,..., xn , по которым найдем среднеарифметическое
1/ n( x1 ... xn ) ,
которое также будет случайно, так как оно зависит от n и выборки. Однако, естественно предположить, что при увеличении n оно
будет приближаться к некоторому неслучайному числу (аналогичное допущение относительно частоты наступления некоторого
события лежит в основе ТВ). Это число и естественно принять за средний рост взрослого человека – среднее с.в.

18.

2.7.1 Характеристики положения
Мы рассмотрим три такие характеристики: математическое ожидание, моду и медиану. Пусть производится n независимых опытов,
в каждом из которых с.в. ξ принимает определенное значение из множества {x1 ,..., xm } . Предположим, что x1 появилось n1 раз, x2
появилось n2 раз и т.д., причем
m
n n.
i 1 i
Имеем
m
m
i 1
i 1
I n ( x1n1 ... xm nm ) / n xi ni / n xi n (i ) .
Так как при увеличении n частота n (i ) появления xi -го значения приближаться к вероятности p i , то I n , в свою очередь, будет
приближаться к величине
m
x p
i 1
i
i
.
Эти соображения приводят к следующим определениям.
Математическим ожиданием д.с.в. называется число
i 1
i 1
M ( ) xi P{ : ( ) xi } xi pi ,
если для с.в, принимающей счетное число значений ряд абсолютно сходится. Если ряд не сходится, то говорят, что м.о. с.в. не
существует. Если множество значений с.в. конечно и
P{ : ( ) xi } 1/ n, i 1,..., n ,
то
n
M ( ) 1 / n xi .
i 1

19.

При определении м.о. для н.с.в. сумма заменяется интегралом
M ( ) xf ( x)dx ,
если интеграл абсолютно сходится. Пусть g ( ) , тогда
i 1
M g ( xi ) pi , M
g ( x) f ( x)dx
для д. и н. с.в., соответственно. Пусть g ( , ) . Тогда
M g ( xi , y j ) pij , M
i 1 j 1
g ( x, y) f ( x, y)dxdy .
Свойства м.о.
1. Если const , то M const . Действительно, постоянную величину можно рассматривать, как с.в., принимающую с
вероятностью 1 постоянное значение.
2. M (c ) cM . Действительно,
M (c ) (cx) f ( x)dx c xf ( x)dx cM .

20.

3. M ( 1 2 ) M 1 M 2 . Доказательство. Положим 1 2 . Тогда
M
( x y) f ( x, y)dxdy xf ( x, y)dxdy yf ( x, y)dxdy
xf1 ( x)dx
yf
2
( y )dy M 1 M 2 .
4.Если 1 , 2 независимы, то
M ( 1 2 ) M 1M 2 .
Доказательство. Положим 1 2 . Тогда
M
xyf ( x, y)dxdy
xyf ( x) f
1
2
( y )dxdy M 1 M 2 .
Модой н.с.в. называется точка локального максимума п.р. Модой д.с.в. называется такое ее значение xi , что pi 1 pi и pi 1 pi .
Различают унимодальные, бимодальные и мультимодальные распределения.
Пример. С.в. – число выпавших Г при двукратном подбрасывании. МОДА=1.
Медианой д.с.в. называется число левее которого лежит половина значений, принимаемой ей, н.с.в. – такое ее значение xm для
которого
P( xm ) P( xm ) 1/ 2 .
Пример. С.в. – число выпавших Г при двукратном подбрасывании. xm 1 .
Имеются ли случаи, когда м.о., медиана и мода совпадают? Это будет справедливо для симметричной относительно м.о. п.р.

21.

22.

2.7.2 Дисперсия
Наблюдаемые значения с.в. могут группироваться вокруг м.о. по-разному – более тесно и наоборот более широко.
Пример. Пусть наблюдаются значения с.в.:
9,7,10,13,11,8,9,10,8,12.
Ср.ар. равно 9.7. Отклонения от него находятся в пределах от -2.7 до 3.3. Пусть теперь наблюдаются значения другой с.в.:
11,9,8,15,9,6,11,8,10,10.
Ср.ар. тоже, но имеются большие отклонения от него – от -3.7 до 5.3. Как охарактеризовать ˝кучность˝ наблюдений возле среднего?
Для этого используется величина, называемая дисперсией и среднеквадратическое отклонение (с.к.о.) - положительный корень из
дисперсии.
Пусть x1 ,..., xn , значения с.в. Положим
m
m
i 1
i 1
J n ( xi I n ) 2 / n, I n xi / n .
Для первого случая J n 3.21, J n1 / 2 1.8 , для второго J n 5.2, J n1 / 2 2.3 . Таким, образом, введенные величины ˝схватывают˝ различный
разброс в данных.

23.

При увеличении n величина n величина I n приближается к м.о. и мы имеем
m
J n ( xi M ) 2 / n .
i 1
Положим
yi ( xi M ) 2 .
Очевидно, что yi есть значение с.в
( M ) 2 .
Ср.ар. ее значений приближается к ее м.о.
D M ( M ) 2 ,
которое называется дисперсией с.в., а корень ( D )1/ 2 - среднеквадратическим отклонением (с.к.о.). Имеем также
D M ( M ) 2 M ( 2 2 M (M ) 2 ) M ( 2 ) (M ) 2 .
Для д. и н.с.в. выражения для дисперсии, с учетом определений предыдущего раздела, могут быть представлены в следующем виде
D ( ) ( xi M ) pi , D ( ) ( x M ) 2 f ( x)dx .
2
i 1
Свойства дисперсии
1. D 0 - следует из определения.
2. D(a b ) b 2 D , a, b - произвольные постоянные. Действительно, пусть a b . Тогда
D(a b ) D M ( M ) 2 M ( a bM ) 2 M (a b a bM ) 2 b 2 D .

24.

3.Если , независимы, то
D( ) D D .
Доказательство.
D( ) M ( M ( ) 2 ) M (( M ) ( M )) 2
M ( M ) 2 M ( M ) 2 2M (( M )( M )) .
Но так как с.в , независимы, то будут независимыми и с.в. M , M . Поэтому из свойства 4 для м.о. следует сделанное
утверждение.
2.7.3 Моменты случайных величин
М.о. и дисперсия наиболее часто, используемые характеристики с.в, они схватывают важные черты распределения – его положение
и степень разброса относительно него. Помимо их используются также и некоторые другие характеристики. Будем называть
начальным моментом k-го порядка число
k M ( k ) ,
а число
k M ( M ) k
центральным моментом k-го порядка. Отметим, что первый центральный момент равен нулю, а второй – дисперсии. Если п.р.
симметрична относительно м.о., то все 2 k 1 равны нулю. Покажем это. Имеем
2 k 1 ( x a)
2 k 1
a
f ( x)dx ( x a)
2 k 1
f ( x)dx ( x a) 2 k 1 f ( x)dx, a M .
a
Делая замену x a y, t a u , получим
0
2 k 1 y
2 k 1
f ( y a)dy ( u)
0
2 k 1
0
f (a u)du y
2 k 1
0
f ( y a)dy u 2 k 1 f (a u)du 0 .

25.

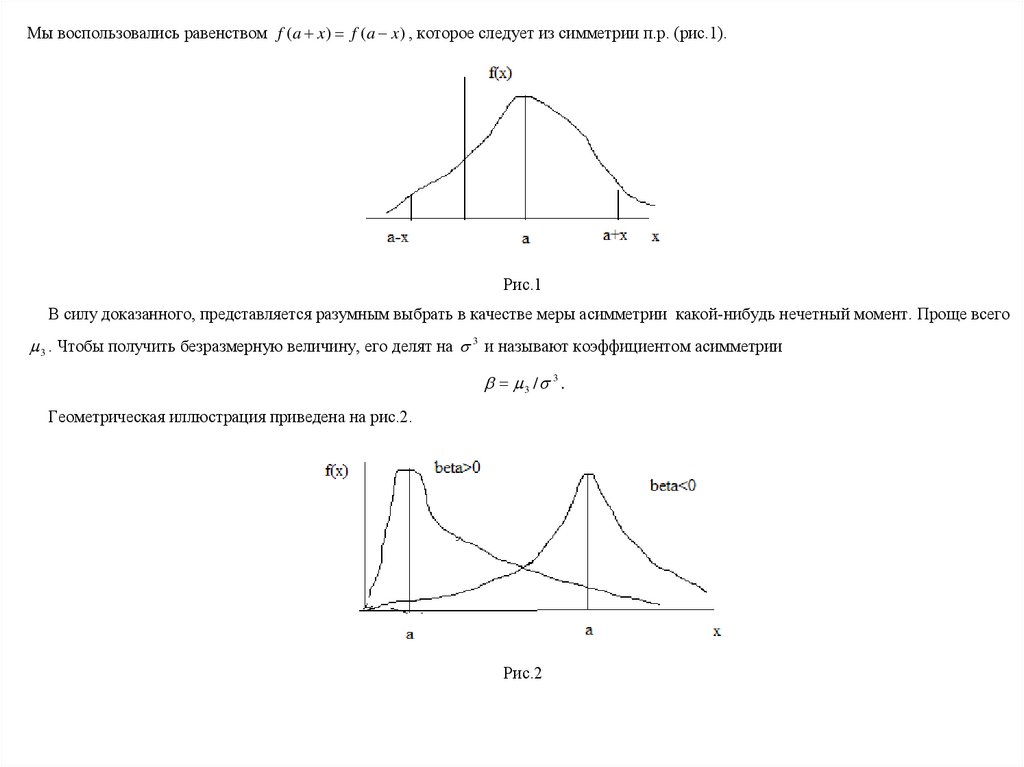
Мы воспользовались равенством f (a x) f (a x) , которое следует из симметрии п.р. (рис.1).
Рис.1
В силу доказанного, представляется разумным выбрать в качестве меры асимметрии какой-нибудь нечетный момент. Проще всего
3 . Чтобы получить безразмерную величину, его делят на 3 и называют коэффициентом асимметрии
3 / 3 .
Геометрическая иллюстрация приведена на рис.2.
Рис.2

26.

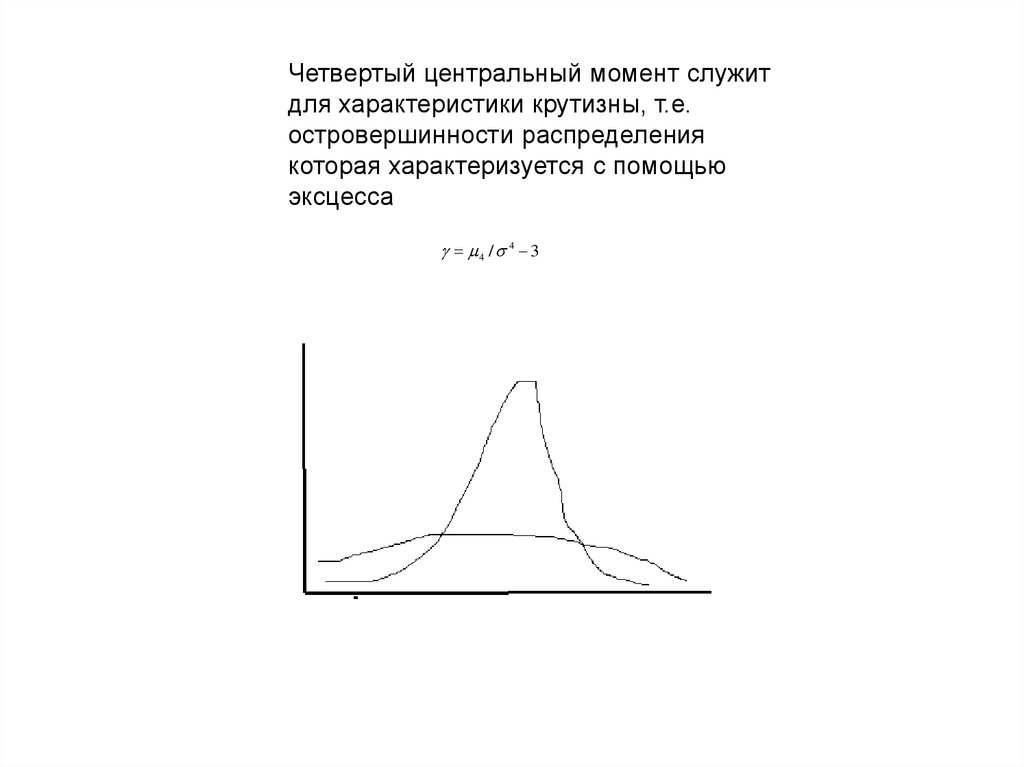
Четвертый центральный момент служит
для характеристики крутизны, т.е.
островершинности распределения
которая характеризуется с помощью
эксцесса
4 / 4 3

27.

2.7.4 Ковариация и корреляция случайных величин
Вспомним, что понимается под независимостью с.в. С.в. ξ и η будем называть независимыми, если
F ( x1 , x2 ) F1 ( x1 ) F2 ( x2 ) .
Т.е. зная значение, которое приняла η, мы никакой новой информации о распределении ξ не получаем. Пусть ξ и η независимые с.в.
Тогда
P({a 1 b, c 2 d}) F (b, d ) F (a, d ) F (b, c) F (a, c) P({a 1 b})P({c 2 d}) .
Т.е. независимыми являются не только события попадания с.в. на полубесконечные интервалы, но и на любые другие.
Пример. 1.Требуется найти время пребывания покупателя в магазине, если количество человек в очереди i.
Будем называть ковариацией величину
cov( , ) M (( M )( M ) .
Для дискретного и непрерывного случаев она имеет вид
cov( , ) ( xi M )( yi M ) pij ,
i 1 j 1
cov( , )
( x M )( y M ) f ( x, y)dxdy .

28.

Ковариация обладает следующими свойствами.
1. cov( , ) D ;
2.Для независимых с.в.
cov( , ) 0 .
Однако обратное, вообще говоря, неверно. Существуют зависимые с.в., ковариация которых равна нулю.
Пример.
Пусть
2
-
связаны
функционально
и
п.р.
,
симметрична,
M 0 .
причем
cov( , ) M [ ( 2 M 2 )] M 3 0.
3. cov( , ) M ( ) M M - следует из определения.
4. D( ) D D 2 cov( , ).
5. | cov( , ) | [ D( ) D( )]1 / 2 . Действительно, положим x . Тогда
D x 2 D D 2 x cov( , ) .
(1)
Найдем точку минимума по x этой функции. Имеем
( D ) (1) xD 2 cov( , ) 0 .
Откуда
xmin cov( , ) / D .
Так как
( D ) ( 2) 2 D 0 ,
то это действительно точка минимума. Геометрическая иллюстрация приведена на рис.1.
(2)
Имеем

29.

Рис.1
Подстановка этого выражения в (1) дает
( D ) min (cov( , ) / D ) 2 D D 2 cov( , ) / D cov( , ) 0 .
Откуда следует свойство 5.
Другое доказательство. Как функция x дисперсия представляет собой квадратный трехчлен, дискриминант которой должен быть
не положительным
2 cov( , ) 2 4D( ) D( ) 0 .
Откуда следует, сделанное утверждение.
Итак, ковариацию можно считать мерой независимости с.в. Но можно ввести более удобную, безразмерную характеристику,
коэффициент корреляции
cov( , ) /[ D( ) D( )]1/ 2 .
К.к. имеет следующие свойства.
1. ( , ) 1 .
2.Для независимых с.в. ( , ) 0 .
3. | ( , ) | 1 .

30.

4.Если a b , где a 0, b постоянные, то | ( , ) | 1 , причем, если a 0, то 0 , если a 0 , то 0 .
Доказательство.
cov( , ) M [( a b b am )( m )] aD , D M (a b b am ) 2 a 2 D .
Поэтому
1, a 0
.
1, a 0
aD /(| a | D )
Это утверждение можно усилить: | ( , ) | 1 , если и только если между с.в. имеется линейная связь. Если ( , ) 0 , то между с.в.
не имеется линейной связи.
Геометрическая иллюстрация к.к. приведена на рис.2.
Рис.2
С помощью ковариации можно ввести ковариационную матрицу для описания векторных с.в. Пусть задана в.с.в. ( 1 ,..., n ) . Тогда
ковариационной матрицей называют симметричную n*n матрицу вида C {cov( i , j )} на диагонали, которой стоят дисперсии.

31.

2.7.5 Условное математическое ожидание
Вспомним, что понимается под условными функциями распределения.
Рассмотрим две с.в. , с совместной функцией распределения F ( x, y ) . Пусть известно, что приняла значение y . Что можно
сказать при этом о распределении ?
Пример. Требуется найти время пребывания покупателя в магазине, если количество человек в очереди i.
Пусть является дискретной с.в. Тогда по определению
F ( x / y ) P({ x / y}) P({ x, y}) / P({ y})
По аналогии
P({ x / y}) P({ x, y}) / P({ y}) .
(1)
Пусть вначале с.в. , дискретны. Будем называть условным м.о. число
n
M ( / y j ) xi P( xi / y j ) ,
i 1
которое описывает среднее значение при условии, что y j .
У.м.о. зависит от значения y j с.в. и поэтому может рассматриваться как функция от с.в. M ( / ) q( ) , т.е. как с.в. Обладает
следующими свойствами:
1. M (c / ) c .
2. M (a b / ) aM ( / ) b .
3. M ( / ) M ( / ) M ( / ) .

32.

4. M M [ M ( / )] .
5. M ( / ) M , если , независимы.
Докажем свойство 4. Из определений м.о. и у.м.о. имеем
n
n
n
n
n
j 1
j 1
i 1
j 1
i 1
M [ M ( / )] M [q( )] M ( / y j ) p j p j xi P( xi / y j ) p j xi pij / p j
n
n
n
n
i 1
j 1
xi pij xi pij M .
j 1 i 1
При доказательстве мы воспользовались
M g ( xi , y j ) pij , M
i 1 j 1
g ( x, y) f ( x, y)dxdy
и дискретным аналогом свойства
6. F1 ( x1 ) F ( x1 , )
x1
x2
f ( x , x )dx dx , F ( x ) F ( , x ) f ( x , x )dx dx
1
2
1
2
2
2
2
1
2
2
1
из раздела 2.3
n
p i pij ,
j 1
где
p i P( xi ) , p j P ( y j ) , pij P( xi , y j ) .
В случае н.с.в. у.м.о. определяется выражением
M ( / )
xf ( x / y)dx ,
где f ( x / y ) f ( x, y ) / f ( y ) - условная плотность распределения.