Похожие презентации:
Системы случайных величин
1.
Системыслучайных величин
2.
Упорядоченный набор ( X 1 , X 2 , , X n ) случайныхвеличин X i (i 1, n) называется n мерной случайной
величиной или системой n случайных величин.
Каждая из величин X i (i 1, n) называется
компоненто й или составляющ ей величины
( X 1 , X 2 , , X n ).
Будем рассматривать в дальнейшем двумерные
случайные величины ( X , Y ).
Системы случайных величин бывают дискретные,
непрерывные и смешанные.
3.
Законом распределения дискретной двумернойслучайной величины ( X , Y ) называют перечень возможных
значений ( xi , y j ) этой величины и их вероятностей
pij P( X xi , Y y j ), где i 1, n, j 1, m.
Обычно закон распределения дискретной двумерной
случайной величины задают в виде таблицы.
X \Y
x1
x2
xi
xn
y1
p11
p21
pi1
pn1
y2
p12
p22
pi 2
pn 2
yj
p1 j
p2 j
pij
pnj
ym
p1m
p2 m
pim
pnm
4.
Для случайной величины ( X , Y ) должно выполнятьсяусловие
n
m
p 1.
i 1 j 1
ij
Зная закон распределения двумерной дискретной
случайной величины, можно найти законы распределения
для компонент :
m
n
j 1
i 1
P( X xi ) pij , P(Y y j ) pij .
Универсальной формой задания двумерной (дискретной
или непрерывной ) случайной величины является функция
распределения.
5.
Функцией распределения двумерной случайной величины( X , Y ) называют
F ( x, y ) P( X x, Y y ).
Геометрически F ( x, y ) равна
вероятности попадания в бесконечный
квадрант лежащий левее и ниже
точки ( x, y ).
Свойства функции распределения
1) 0 F ( x, y ) 1.
2) F ( x1 , y ) F ( x2 , y ), если x1 x2 ,
F ( x, y1 ) F ( x, y2 ), если y1 y2 .
3) F ( , y ) F ( x, ) F ( , ) 0.
4) F ( , ) 1.
6.
5) F ( x, ) F1 ( x) функция распределения случайнойвеличины X ,
F ( , y ) F2 ( y ) функция распределения случайной
величины Y .
6) Если X и Y независимы, то F ( x, y ) F1 ( x) F2 ( y ).
7) P( x1 X x2 , y1 Y y2 ) F ( x2 , y2 ) F ( x1 , y2 )
F ( x2 , y1 ) F ( x1 , y1 ) .
7.
Непрерывную двумерную случайную величину можнозадавать с помощью плотности вероятности.
Плотностью распределения вероятност ей двумерной
непрерывной случайной величины ( X , Y ) называют функцию
2F
f ( x, y )
,
x y
где F функция распределения случайной величины ( X , Y ).
Свойства плотности распределения
1) f ( x, y ) 0.
2) P ( X , Y ) D f ( x, y )dxdy.
D
3) f ( x, y )dxdy 1.
8.
y x4) F ( x, y ) f ( x, y )dxdy.
5) f ( x, y )dy f1 ( x) плотность распределения X ,
f ( x, y)dx f ( y) плотность распределения Y .
2
6) Если X и Y независимы, то f ( x, y ) f1 ( x) f 2 ( y ).
Рассмотрим основные характеристики системы
двух случайных величин.
9.
Корреляционным моментом (или ковариацией)случайных величин X и Y называют математическое
ожидание произведения отклонений этих величин :
xy cov( X , Y ) M [( X M ( X )) (Y M (Y ))].
n
m
xy ( xi M ( X ))( y j M (Y )) pij для дискретных
i 1 j 1
случайных величин.
xy ( x M ( X ))( y M (Y )) f ( x, y )dxdy для непрерывных
случайных величин.
Корреляционный момент двух независимы х случайных
величин X и Y равен нулю.
10.
Коэффициен том корреляции rxy двух случайныхвеличин X и Y называют отношение ковариации к
произведению средних квадратических отклонений
этих величин
cov( X , Y )
rxy
.
( X ) (Y )
Свойства коэффициен та корреляции
1) 1 rxy 1.
2) rxy 0, если X и Y независимы.
3) Если rxy 1, то X и Y связаны линейной функционал ьной
зависимостью Y aX b.
11.
Предельные теоремы12.
Здесь рассматривается ряд утверждений и теорем избольшой группы так называемых предельных теорем теории
вероятностей, устанавливающих связь между теоретическими
и эксперимен тальными характеристиками случайных величин
при большом числе испытаний над ними. Предельные теоремы
условно делят на две группы.
Первая группа теорем, называемая центрально й предельной
теоремой (коротко : ЦПТ ), устанавливает условия, при которых
закон распределения суммы большого числа случайных величин
неограниченно приближается к нормальном у.
Вторая группа теорем, называемая законом больших чисел
(коротко : ЗБЧ ), устанавливает устойчивость средних значений :
при большом числе испытаний их средний результат перестает
быть случайным и может быть предсказан с достаточной
точностью.
13.
Центральная предельнаятеорема
14.
Нормально распределенные случайные величины широкораспространены на практике. Отмечено, что если случайная
величина X представляет собой сумму очень большого числа
взаимно независимых случайных величин, влияиние каждой из
которых на всю сумму ничтожно мало, то X имеет
распределение, близкое к нормальному. Объяснение этому
факту дает группа теорем под общим названием
центральна я предельная теорема ( ЦПТ ). Поясним как
формулируются теоремы, относящиеся к ЦПТ.
15.
Пусть X 1 , X 2 , , X k , последовательность независимыхслучайных величин, каждая из которых имеет конечные
математическое ожидание и дисперсию :
M ( X k ) ak , D( X k ) bk2 (k 1,2, ).
Введем обозначения :
n
n
n
S n X k , An ak , B bk2 .
k 1
k 1
2
n
k 1
Обозначим функцию распределения нормированной суммы
через
S n An
Fn ( x) P
x .
Bn
16.
Говорят, что к последовательности X 1 , X 2 , , X k ,применима центральная предельная теорема, если при любом
x R функция распределения нормированной суммы при n
стремится к нормальной функции распределения :
x
1
lim Fn ( x) ( x)
e
n
2
t2
2
dt.
В частности ЦПТ применима , если :
1) X 1 , X 2 , , X k , одинаково распределены.
2) Выполняется условие Ляпунова :
n
Cn
2
0 при n : Ln 2 0, где Cn M X k ak
.
Bn
k 1
17.
Пример. Независимы е случайные величины X 1 , X 2 , , X k ,распределены равномерно на отрезке [0,1]. Найти закон
распределения случайной величины
100
Y Xk,
k 1
а также вероятность того, что 55 Y 70.
Условия ЦПТ соблюдаются (случай 1), поэтому случайная
величина Y имеет приближенно плотность распределения
fY ( x)
1
Y 2
e
( x aY ) 2
2 Y2
.
Для равномерного распределения имеем :
0 1 1
M (Xk )
,
2
2
(1 0) 2 1
D( X k )
.
12
12
18.
Тогда1
100
100
aY M (Y ) M X k M ( X k ) 100 50,
2
k 1 k 1
1 25
100
100
2
Y D(Y ) D X k D( X k ) 100 ,
12 3
k 1 k 1
25 5 3
Y
.
3
3
Поэтому
3
fY ( y )
e
5 6
3( y 50) 2
50
.
19.
Для нормальног о распределения X с математическиможиданием a и средним квадратическим отклонением
справедлива формула
a
a
P( X )
.
Тогда
70 50
55 50
4 3 3
P(55 Y 70)
5
3
3
5
3
3
(6,9282) (1,73) 0,04,
Таким образом,
P(55 Y 70) 0,04.
20.
Таким образом, ЦПТ объясняет причину того, чтонормально распределенные случайные величины широко
распространены на практике. Если же распределение
отлично от нормального, то может возникнуть
необходимость количественной оценки такого отличия.
С этой целью используют асимметрию и эксцесс. Для
нормальног о распределения эти величины равны нулю.
Поэтому, если для изучаемого распределения они малы,
то можно предположить близость этого распределения
к нормальном у и наоборот.
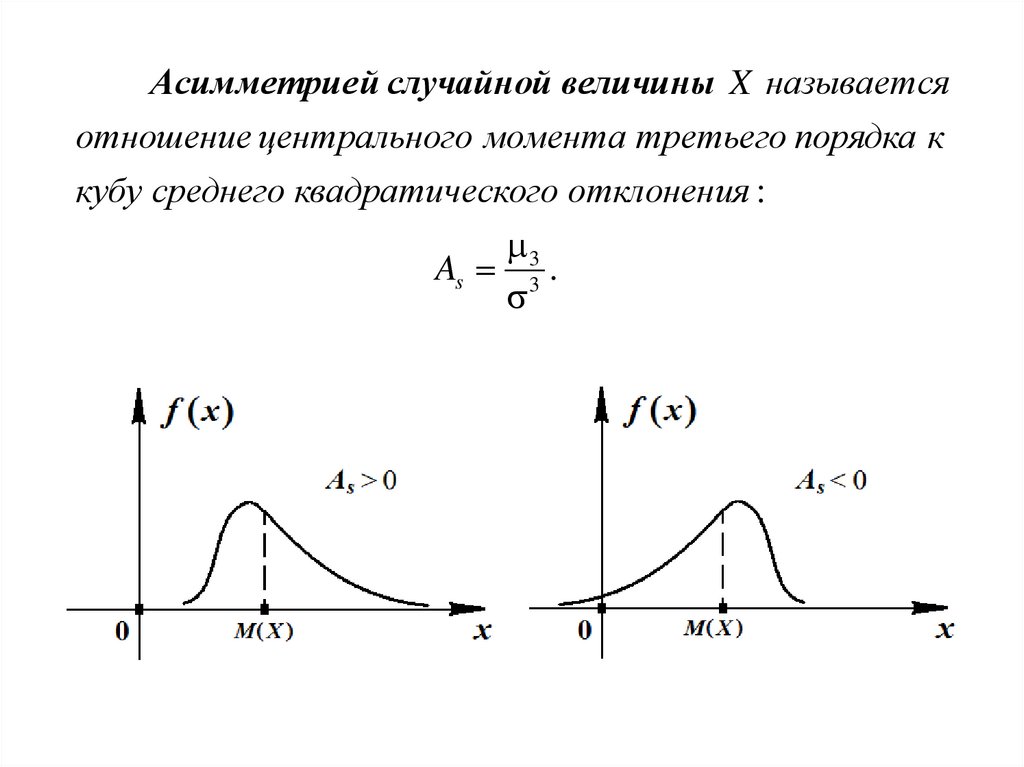
21.
Асимметрие й случайной величины X называетсяотношение центрального момента третьего порядка к
кубу среднего квадратического отклонения :
3
As 3 .
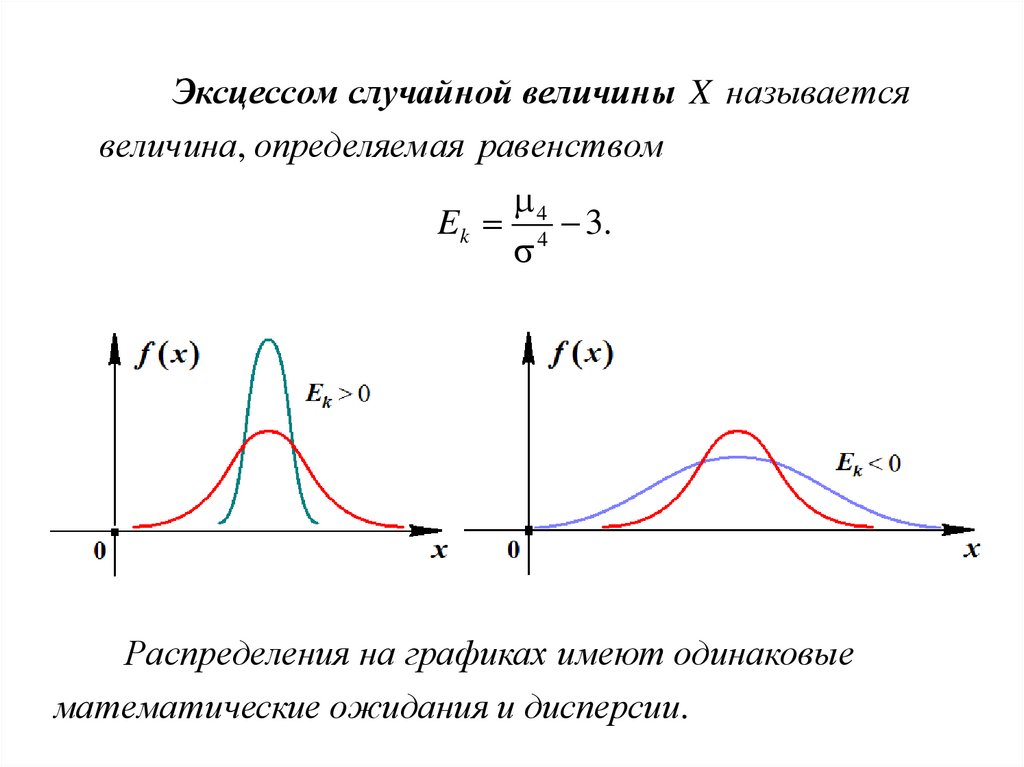
22.
Эксцессом случайной величины X называетсявеличина, определяем ая равенством
4
E k 4 3.
Распределения на графиках имеют одинаковые
математические ожидания и дисперсии.
23.
Закон больших чисел24.
Как известно, нельзя заранее предвидеть, какое извозможных значений примет случайная величина при
испытании. Однако , при выполнении некоторых условий
суммарное поведение достаточно большого числа
случайных величин почти утрачивает случайный
характер и становится закономерн ым. Такие условия
указываются в теоремах, носящих общее название
закона больших чисел ( ЗБЧ ).
25.
Теорема (неравенств о Чебышева ). Вероятност ь того,что отклонение случайной величины X от ее математического
ожидания по абсолютной величине не меньше положительного
числа меньше или равна отношению дисперсии случайной
величины X к квадрату числа :
D( X )
P ( X M ( X ) )
.
(1)
2
Доказатель ство. Обозначим a M ( X ), тогда
x a
P( X M ( X ) ) f ( x)dx
f ( x)dx
x a
x a
2
1
1
D( X )
2
2
2 ( x a) f ( x)dx 2 ( x a) f ( x)dx
.
2
x a
26.
Следствие. Неравенство Чебышева можно записать и вдругой форме :
D( X )
P ( X M ( X ) ) 1 2 .
(2)
Пример. Оценить с помощью неравенства Чебышева
вероятность того, что отклонение случайной величины X от
своего математического ожидания меньше трех средних
квадратических отклонений.
D( X )
2 8
P( X M ( X ) 3 ) 1
1 2 0,888
2
(3 )
9
9
27.
Теорема (Чебышева ). Если X 1 , X 2 , , X n , попарнонезависимые случайные величины, причем их дисперсии не
превысшают постоянного числа C , то, как бы мало ни было
положительное число , вероятность неравенства
X1 X 2 X n M ( X1) M ( X 2 ) M ( X n )
n
n
будет как угодна близка к единице, если число случайных
величин достаточно велико, то есть
X X 2 X n M ( X1) M ( X 2 ) M ( X n )
lim P 1
1.
n
n
n
28.
Доказатель ство . ОбозначимX1 X 2 X n
X
,
n
тогда
X1 X 2 X n 1 n
M (X ) M
M ( X k ).
n
n k 1
Применяя к X неравенство Чебышева (2), получим
D( X )
P X M ( X ) 1 2
или
1 1 n
P X M ( X ) 1 2 D X k .
n k 1
Заметим, что
(3)
29.
1 n1 n
1
D X k 2 D X k 2 D ( X 1 ) D ( X 2 ) D ( X n )
n k 1 n k 1 n
1
nC C
2 C C C 2 ,
n
n
n
то есть
C
D( X ) .
(4)
n
Подставляя (4) в (3), получаем
D( X )
C
P X M (X ) 1 2 1 2
n
или
X1 X 2 X n M ( X1) M ( X 2 ) M ( X n )
C
P
1 2 .
n
n
n
(5)
30.
Переходя в неравенстве (5) к пределу при n , получаемX1 X 2 X n M ( X1) M ( X 2 ) M ( X n )
lim P
1,
n
n
n
а так как вероятность может принимать значения от 0 до 1,
то, следовательно,
X1 X 2 X n M ( X1) M ( X 2 ) M ( X n )
lim P
1.
n
n
n
Теорема доказана.
Следствие. Если случайные величины X 1 , X 2 , , X n ,
независимы и одинаково распределны ( k N : M ( X k ) a,
D( X k ) ), то для любого 0
X1 X 2 X n
lim P
a 1.
n
n
31.
Пример. Глубина моря измеряется прибором, не имеющимсистематической ошибки. Среднее квадратическое отклонение
измерений не превосходит 15 м. Сколько нужно сделать независимых
измерений , чтобы с вероятностью, не меньшей 0,9, можно было
утверждать, что среднее арифметическое этих измерений
отличается от a ( глубины моря ) по модулю меньше, чем на 5 м ?
Обозначим через X k результаты n независимых измерений
глубины моря (k 1, n). Нужно найти такое n, чтобы выполнялось
неравенство (5) :
1 n
1 n
C
P X k M ( X k ) 1 2 ,
n k 1
n
n k 1
где M ( X k ) a ( это означает, что при измерениях нет
систематических ошибок ).
32.
По условию задачи 5, C 225, так как D( X k ) C , аD( X k ) 2 ( X k ) 152. Тогда
1 n
C
225
P X k a 5 1 2 1
0,9
n
n 25
n k 1
9
0,1
n 90.
n
Таким образом, измерения нужно проводить не менее 90 раз.































 Математика
Математика