Похожие презентации:
Логические основы ЭВМ, элементы и узлы
1.
Логические основы ЭВМ,элементы и узлы
1
2. Алгебра логики
!Алгебра логики – раздел математики, изучающий
высказывания, рассматриваемые с точки зрения их
логических значений (истинности или ложности), и
логические операции над ними.
Джордж Буль (1815-1864) – английский
математик,
основоположник
алгебры
логики. Изучал логику мышления математическими
методами
и
разработал
алгебраические методы решения традиционных логических задач. Долгое время
алгебра логики была известна достаточно
узкому классу специалистов.
В 1938 году Клод Шеннон применил алгебру логики для
описания процесса функционирования релейно-контактных и
электронно-ламповых схем.
3. Высказывания и переменные
!Высказывание – это предложение, в отношении
которого можно сказать, истинно оно или ложно.
!
Высказывания, образованные из других высказываний,
называются составными. Высказывание, никакая часть
которого не является высказыванием, называется
элементарным.
Обоснование истинности или
ложности элементарных
высказываний не является
задачей алгебры логики
4. Высказывания и переменные
Задание 1. Выберите пословицыкоторые являются высказываниями.
Готовь сани летом,
а телегу зимой
В зимний холод
всякий молод
Добра не смыслишь,
так худа не делай
Знание да наука на
вороту не висят
Не в свои сани
не садись!
Ответ
Цыплят по
осени считают
Труд человека кормит,
а лень портит
Не сиди сложа руки,
так и не будет скуки
Береги платье снову,
а честь смолоду
Без труда не вынешь
рыбки из пруда
5.
Составные высказыванияВысказывание “Все мышки и кошки с хвостами”
является сложным и состоит из двух простых высказываний.
А=“Все мышки с хвостами” и В=“Все кошки с хвостами”
Его можно записать в виде логической функции, значение
которой истинно: F(A,B)=A и B
В математической логике не рассматривается конкретное
содержание высказывания, важно только, истинно оно или
ложно. Поэтому высказывание можно представить некоторой
переменной величиной, значением которой может быть
только ложно (0) или истинно (1).
6.
Различают:1. Логические константы (логические утверждения) –
конкретные частные утверждения (И/Л)
{Аристотель - основоположник логики}
{На яблонях растут бананы}
2. Логические переменные (предикаты) – логические
высказывания, значения которых меняются в зависимости
от входящих в них переменных, обозначаются заглавными
латинскими буквами А, В, С, D, F,…
А = {Аристотель - основоположник логики}
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному
— 0. Таким образом, А = 1, В = 0.
7.
Логическая функция - это функция логических переменных,которая может принимать только два значения : 0 или 1. (булева
функция)
Логический элемент - это устройство, реализующее ту или иную
логическую функцию.
Физически логические элементы могут быть выполнены
механическими, электромеханическими (на электромагнитных
реле), электронными (на диодах и транзисторах), пневматическими,
гидравлическими, оптическими и др.
Всего возможно
логических функций и соответствующих им
логических элементов, где x - основание системы счисления, n число входов (аргументов), m - число выходов, т.е. бесконечное
число логических элементов.
7
8.
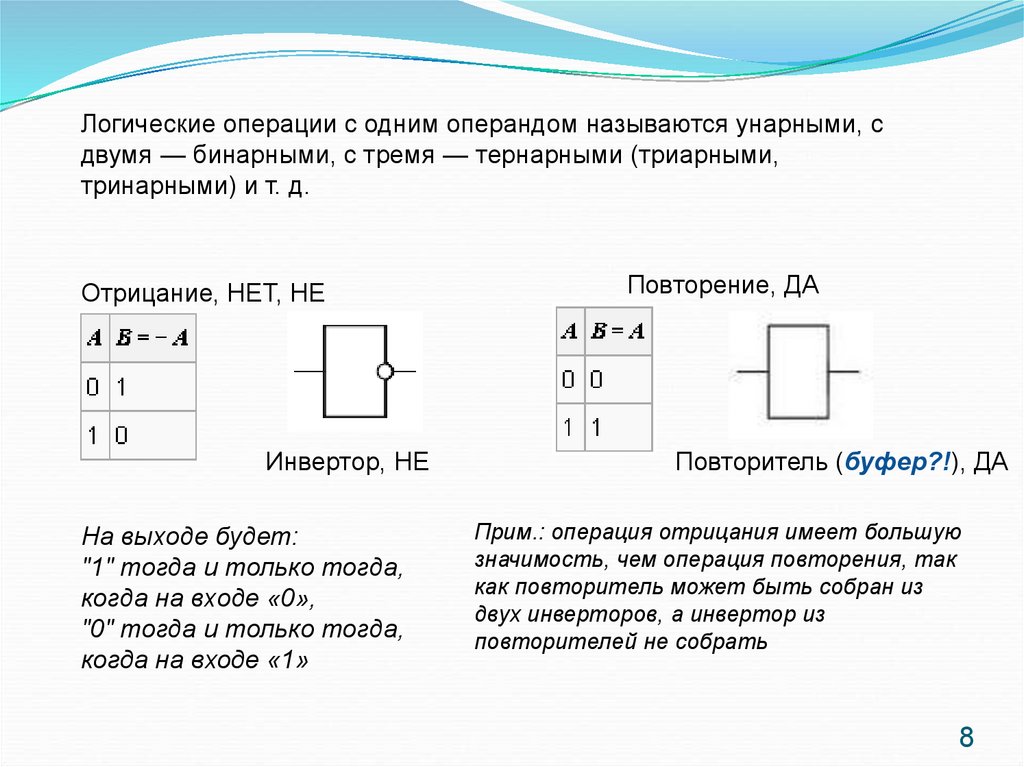
Логические операции с одним операндом называются унарными, сдвумя — бинарными, с тремя — тернарными (триарными,
тринарными) и т. д.
Отрицание, НЕТ, НЕ
Инвертор, НЕ
На выходе будет:
"1" тогда и только тогда,
когда на входе «0»,
"0" тогда и только тогда,
когда на входе «1»
Повторение, ДА
Повторитель (буфер?!), ДА
Прим.: операция отрицания имеет большую
значимость, чем операция повторения, так
как повторитель может быть собран из
двух инверторов, а инвертор из
повторителей не собрать
8
9.
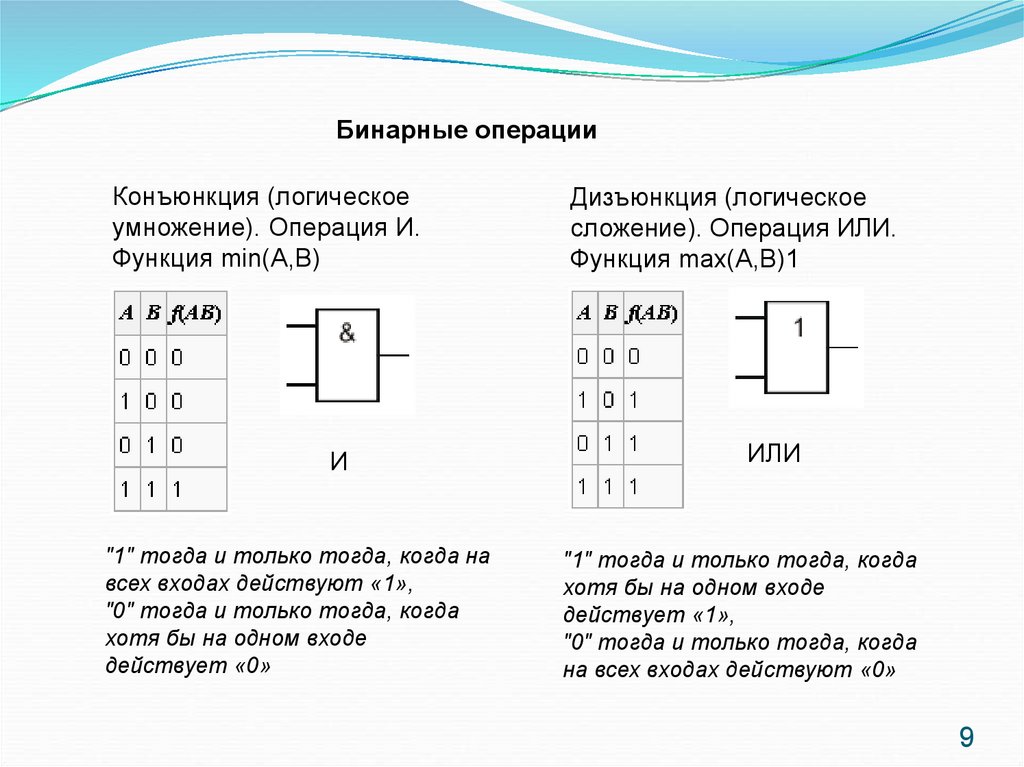
Бинарные операцииКонъюнкция (логическое
умножение). Операция И.
Функция min(A,B)
И
"1" тогда и только тогда, когда на
всех входах действуют «1»,
"0" тогда и только тогда, когда
хотя бы на одном входе
действует «0»
Дизъюнкция (логическое
сложение). Операция ИЛИ.
Функция max(A,B)1
ИЛИ
"1" тогда и только тогда, когда
хотя бы на одном входе
действует «1»,
"0" тогда и только тогда, когда
на всех входах действуют «0»
9
10.
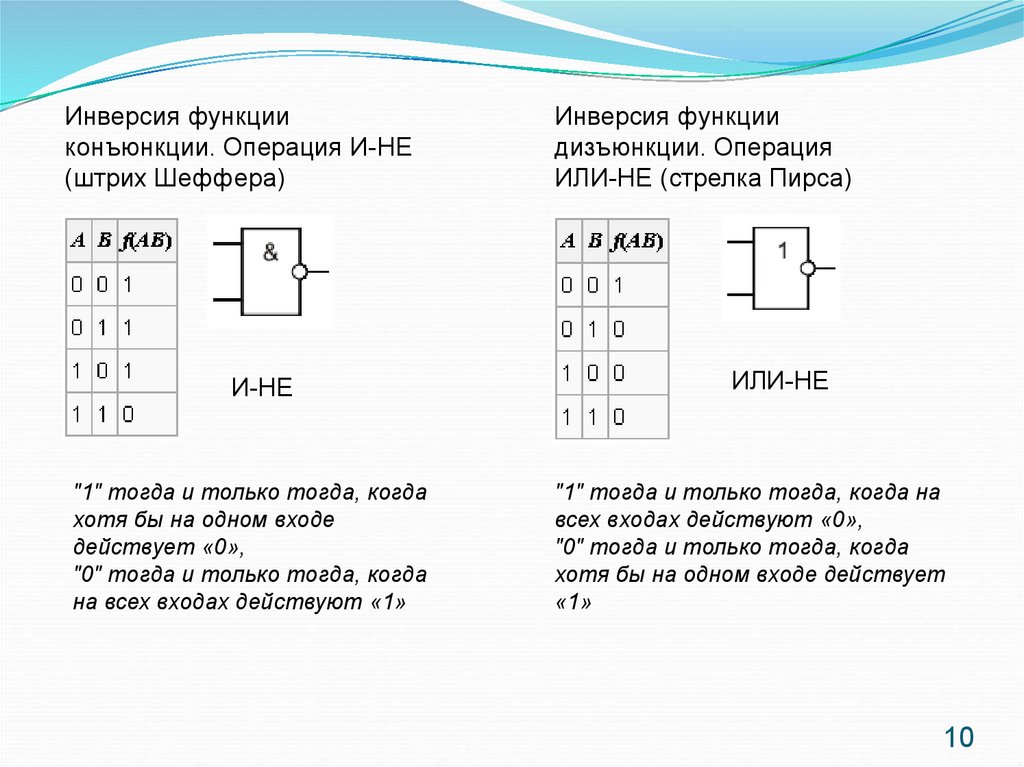
Инверсия функцииконъюнкции. Операция И-НЕ
(штрих Шеффера)
И-НЕ
"1" тогда и только тогда, когда
хотя бы на одном входе
действует «0»,
"0" тогда и только тогда, когда
на всех входах действуют «1»
Инверсия функции
дизъюнкции. Операция
ИЛИ-НЕ (стрелка Пирса)
ИЛИ-НЕ
"1" тогда и только тогда, когда на
всех входах действуют «0»,
"0" тогда и только тогда, когда
хотя бы на одном входе действует
«1»
10
11.
Эквивалентность(равнозначность),
ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
Сложение по модулю 2
(Исключающее_ИЛИ,
неравнозначность). Инверсия
равнозначности.
"1" тогда и только тогда, когда
на входе действует четное
количество «1»,
"0" тогда и только тогда, когда
на входе действует нечетное
количество «1»
"1" тогда и только тогда, когда на
входе действует нечётное
количество «1»,
"0" тогда и только тогда, когда на
входе действует чётное
количество «1»
11
12.
Импликация от A к B (инверсиядекремента)
Импликация от B к A (инверсия
инкремента)
"0" тогда и только тогда, когда
на входе "B" меньше "А",
"1" тогда и только тогда, когда
на входе "B" больше либо равно
"А"
"0" тогда и только тогда, когда
на входе "B" больше "А",
"1" тогда и только тогда, когда
на входе "B" меньше либо равно
"А"
12
13.
Декремент. Запретимпликации по B. Инверсия
импликации от A к B
Инкремент. Запрет
импликации по A. Инверсия
импликации от B к A
"1" тогда и только тогда, когда
на входе "A" больше "B",
"0" тогда и только тогда, когда
на входе "A" меньше либо равно
"B"
"1" тогда и только тогда, когда
на входе "B" больше "A",
"0" тогда и только тогда, когда
на входе "B" меньше либо равно
"A"
13
14.
Этими простейшими логическими операциями (функциями), идаже некоторыми их подмножествами, можно выразить любые
другие логические операции.
Такой набор простейших функций называется функционально
полным логическим базисом. Таких базисов 4:
И, НЕ (2 элемента)
ИЛИ, НЕ (2 элемента)
И-НЕ (1 элемент)
ИЛИ-НЕ (1 элемент).
14
15.
Физические реализации логических элементовФизические реализации одной и той же логической функции в разных
системах электронных и неэлектронных элементов отличаются друг от
друга.
На текущий момент наиболее популярно использование электронных
транзисторных физических реализаций логических элементов.
Логические элементы подразделяются и по типу использованных в них
электронных элементов. Наибольшее применение в настоящее время
находят следующие логические элементы:
•РТЛ (резисторно-транзисторная логика)
•ДТЛ (диодно-транзисторная логика)
•ТТЛ (транзисторно-транзисторная логика)
•ТТЛШ (то же с диодами Шоттки)
•КМОП (логика на основе комплементарных ключей на МОП
транзисторах)
•ЭСЛ (эмиттерно-связанная логика)
15
16.
1617.
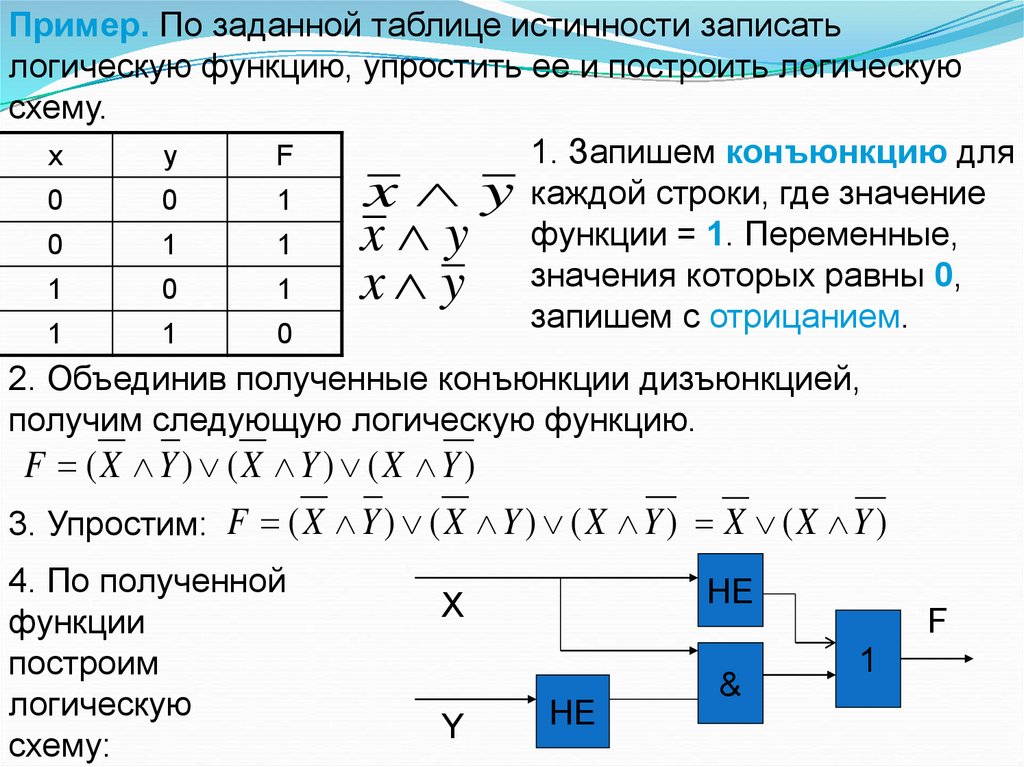
Пример. По заданной таблице истинности записатьлогическую функцию, упростить ее и построить логическую
схему.
1. Запишем конъюнкцию для
x
y
F
x y каждой строки, где значение
0
0
1
x y функции = 1. Переменные,
0
1
1
x y значения которых равны 0,
1
0
1
запишем с отрицанием.
1
1
0
2. Объединив полученные конъюнкции дизъюнкцией,
получим следующую логическую функцию.
F (X Y) (X Y) (X Y)
3. Упростим: F ( X Y ) ( X Y ) ( X Y ) X ( X Y )
4. По полученной
функции
построим
логическую
схему:
НЕ
X
Y
НЕ
&
F
1
18.
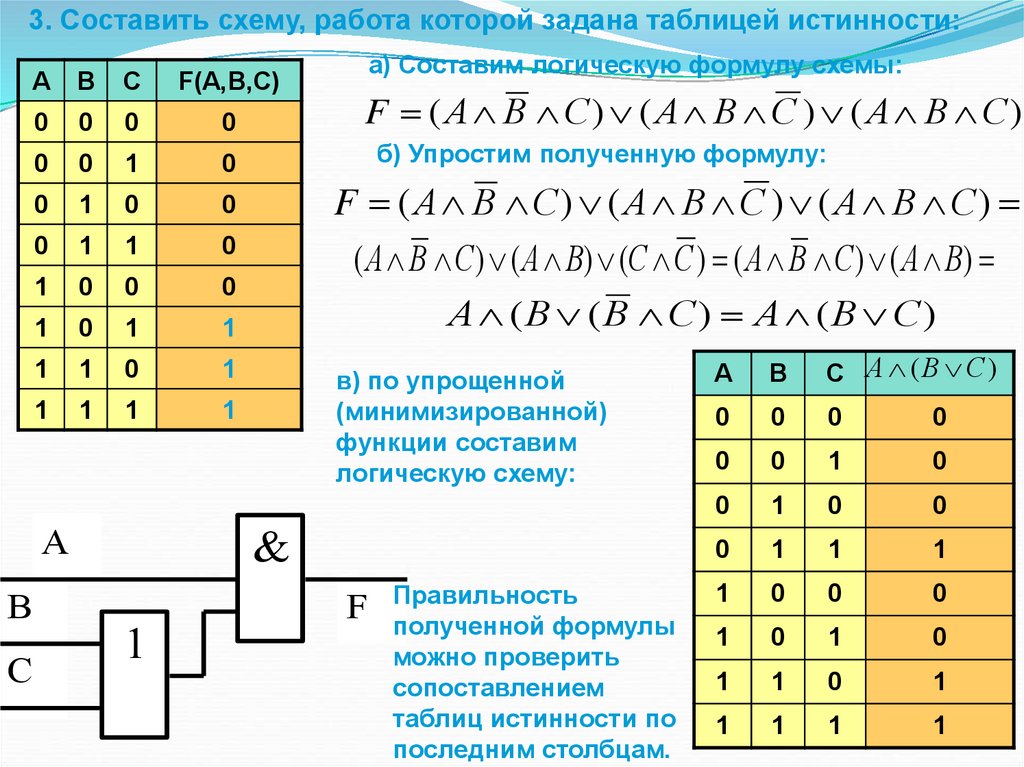
3. Составить схему, работа которой задана таблицей истинности:а) Составим логическую формулу схемы:
A B
C
F(A,B,C)
0
0
0
0
F ( А В С) ( А В С ) ( А В С)
0
0
1
0
б) Упростим полученную формулу:
0
1
0
0
0
1
1
0
1
0
0
0
1
0
1
1
1
1
0
1
1
1
1
1
C
А (В (В С) А (В С)
в) по упрощенной
(минимизированной)
функции составим
логическую схему:
&
A
B
F ( А В С) ( А В С ) ( А В С)
( А В С ) ( А В) (С С ) ( А В С ) ( А В)
1
F Правильность
полученной формулы
можно проверить
сопоставлением
таблиц истинности по
последним столбцам.
A
B
C А (В С)
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
1
1
1
1
1
19.
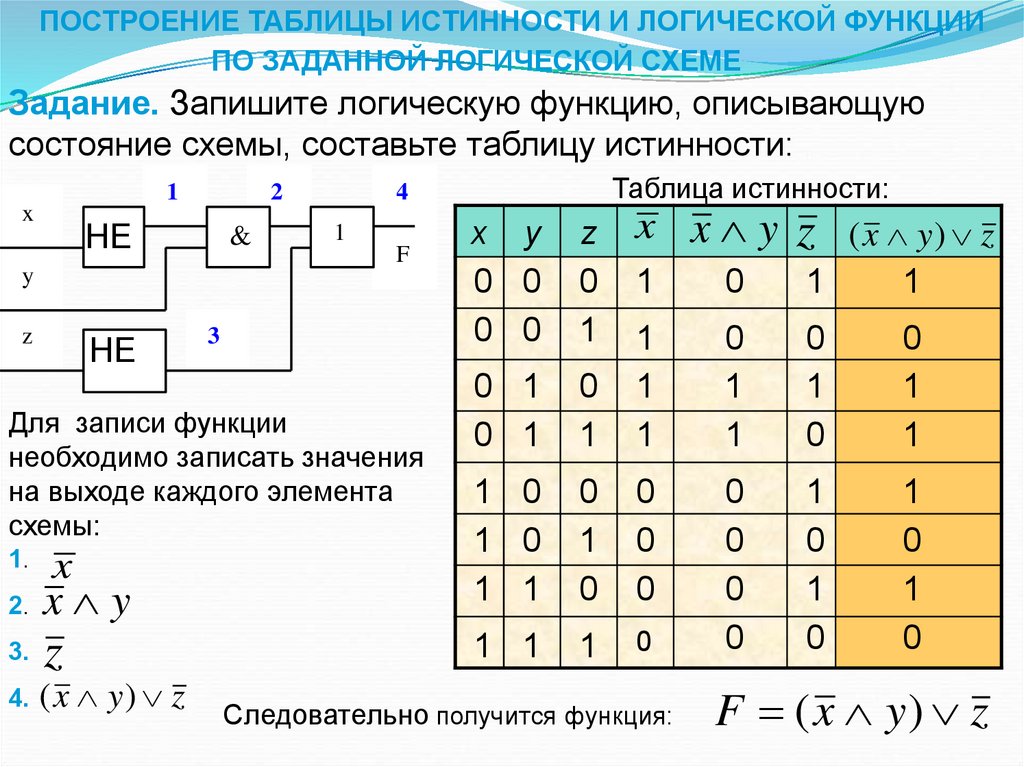
ПОСТРОЕНИЕ ТАБЛИЦЫ ИСТИННОСТИ И ЛОГИЧЕСКОЙ ФУНКЦИИПО ЗАДАННОЙ ЛОГИЧЕСКОЙ СХЕМЕ
Задание. Запишите логическую функцию, описывающую
состояние схемы, составьте таблицу истинности:
1
x
2
НЕ
&
1
F
y
z
НЕ
Таблица истинности:
4
3
Для записи функции
необходимо записать значения
на выходе каждого элемента
схемы:
x y
0 0
0 0
z
0
1
0 1
0 1
2.
x y
1 0
1 0
1 1
3.
z
1 1
1.
x
4. ( x y ) z
x x y z ( x y) z
1
0
1
1
0
1
1
1
1
0
1
1
0
1
0
0
1
1
0
1
0
0
0
0
1
0
0
0
0
0
1
0
1
0
1
0
1
0
Следовательно получится функция:
F ( x y) z
20.
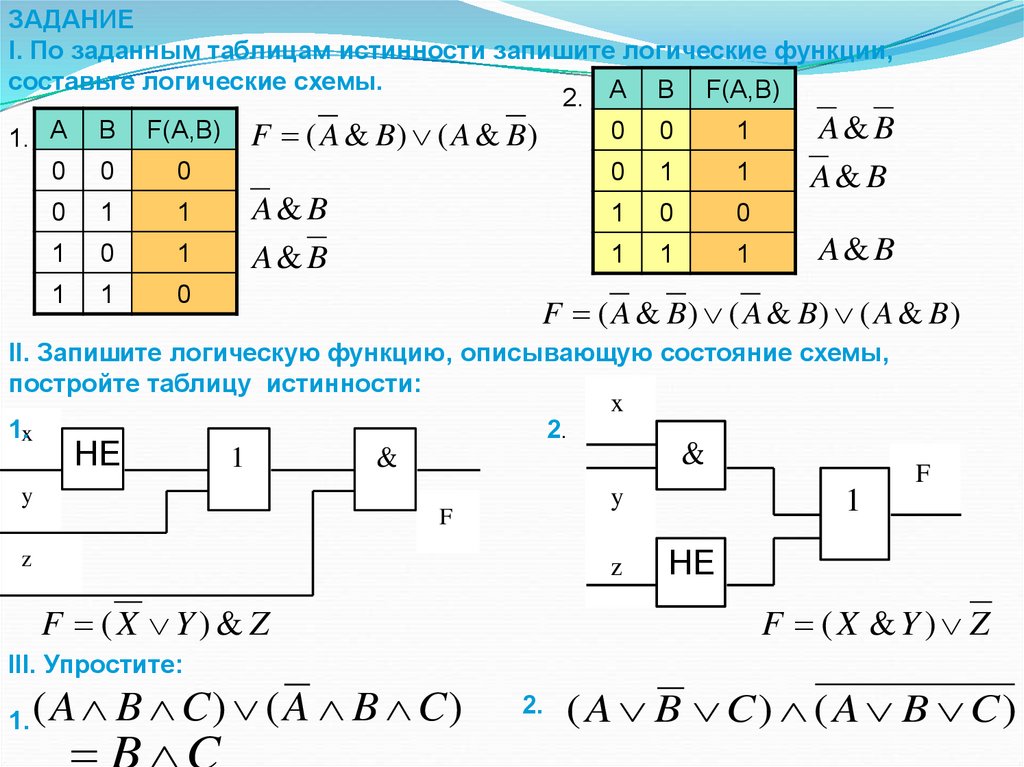
ЗАДАНИЕI. По заданным таблицам истинности запишите логические функции,
составьте логические схемы.
2. A B F(A,B)
A& B
0 0
1
1. A B F(A,B) F ( A & B ) ( A & B )
0
0
0
0
1
1
1
0
1
1
1
0
A& B
A& B
0
1
1
1
0
0
1
1
1
A& B
A& B
F ( A & B) ( A & B) ( A & B)
II. Запишите логическую функцию, описывающую состояние схемы,
постройте таблицу истинности:
x
1.x
2.
НЕ
1
y
&
&
y
F
z
z
F (X Y) & Z
F
1
НЕ
F (X &Y ) Z
III. Упростите:
1.
( A B C) ( A B C)
B C
2.
( A B C) ( A B C)












 Информатика
Информатика








