Похожие презентации:
Статистическая проверка статистических гипотез
1.
Лекция № 16Занятие 4/5
СТАТИСТИЧЕСКАЯ
ПРОВЕРКА
СТАТИСТИЧЕСКИХ
ГИПОТЕЗ
2.
1. Основные понятия статистическойпроверки статистических гипотез.
2. Проверка гипотезы о законе
распределения
дискретной
случайной величины по критерию
Пирсона.
3.
Учебный вопрос №1Основные понятия
статистической проверки
статистических гипотез
4.
Статистическая гипотеза(statistical hypothesis)
любое предположение о свойствах и
характеристиках исследуемых
генеральных совокупностей, которое
может быть проверено на основе
анализа выборок
5.
Метод проверки статистическойгипотезы называется статистическим
критерием.
Статистический критерий строится
на основе имеющейся
выборки x=(x1,…, xI) с помощью
измеримой функции S(x),
называемой статистикой критерия
6.
Статистика критерия(критерий, statistical test)
специальная функция от элементов
выборки, по значениям которой принимают
решение о принятии или отклонении
основной гипотезы.
Статистика зависит от выборки, поэтому
является случайной функцией.
7.
Нулевая и альтернативная гипотезыНулевая (основная) гипотеза
выдвинутая гипотеза H0, которую
нужно применять или отвергнуть.
Гипотеза, которая противоречит
основной Н0, называется
альтернативной или
конкурирующей Н1
8.
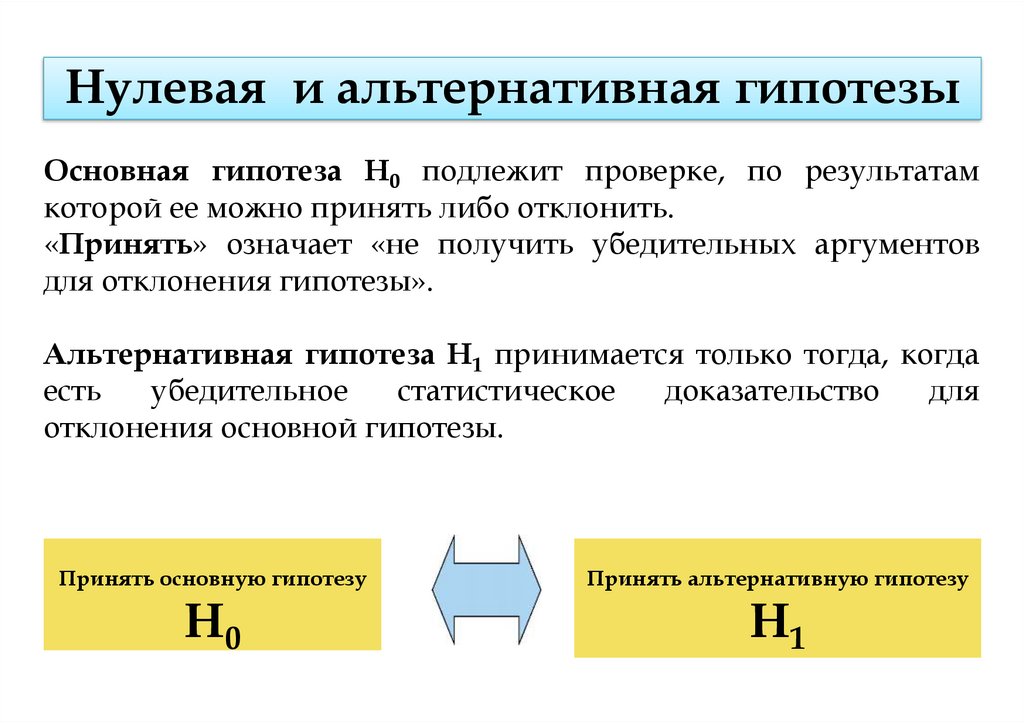
Нулевая и альтернативная гипотезыОсновная гипотеза Н0 подлежит проверке, по результатам
которой ее можно принять либо отклонить.
«Принять» означает «не получить убедительных аргументов
для отклонения гипотезы».
Альтернативная гипотеза Н1 принимается только тогда, когда
есть
убедительное
статистическое
доказательство
для
отклонения основной гипотезы.
Принять основную гипотезу
Принять альтернативную гипотезу
Н0
Н1
9.
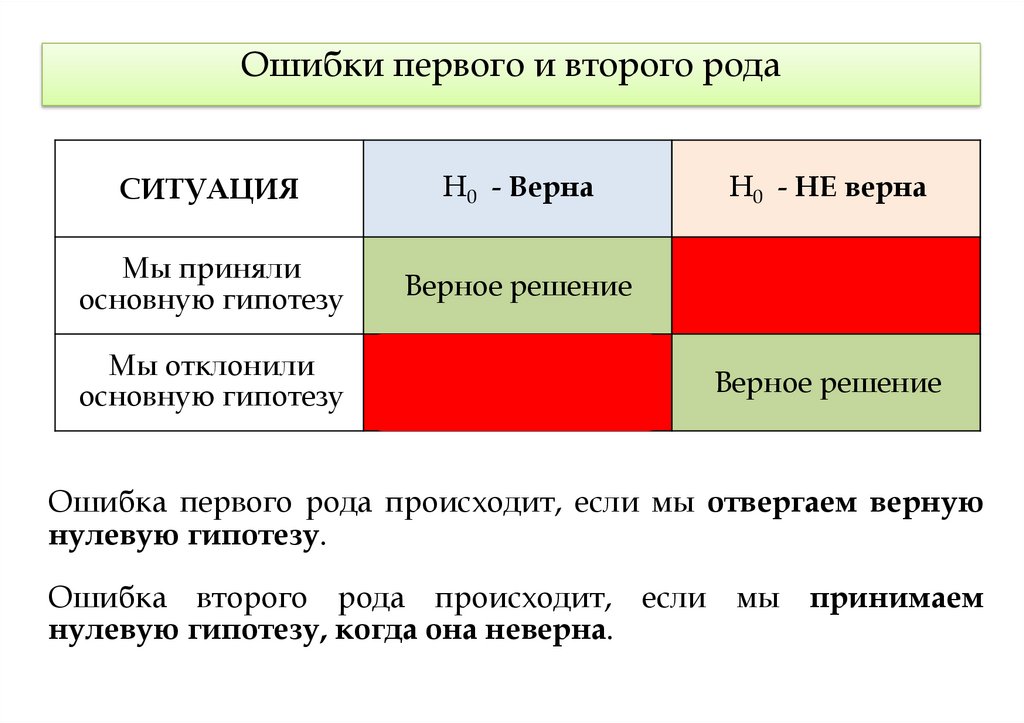
Ошибки первого и второго родаСИТУАЦИЯ
Н0 - Верна
Н0 - НЕ верна
Мы приняли
основную гипотезу
Верное решение
Ошибка II рода
Мы отклонили
основную гипотезу
Ошибка I рода
Верное решение
Ошибка первого рода происходит, если мы отвергаем верную
нулевую гипотезу.
Ошибка второго рода происходит, если мы принимаем
нулевую гипотезу, когда она неверна.
10.
Уровень значимости гипотезыВероятность совершить ошибку первого
рода
Обозначение: α,
Значение α обычно выбирается небольшим:
10%, 5% или 1%.
Если α = 0,05, то в 5 случаях из 100 имеется
риск допустить ошибку I рода, т. е.
отвергнуть правильную гипотезу.
11.
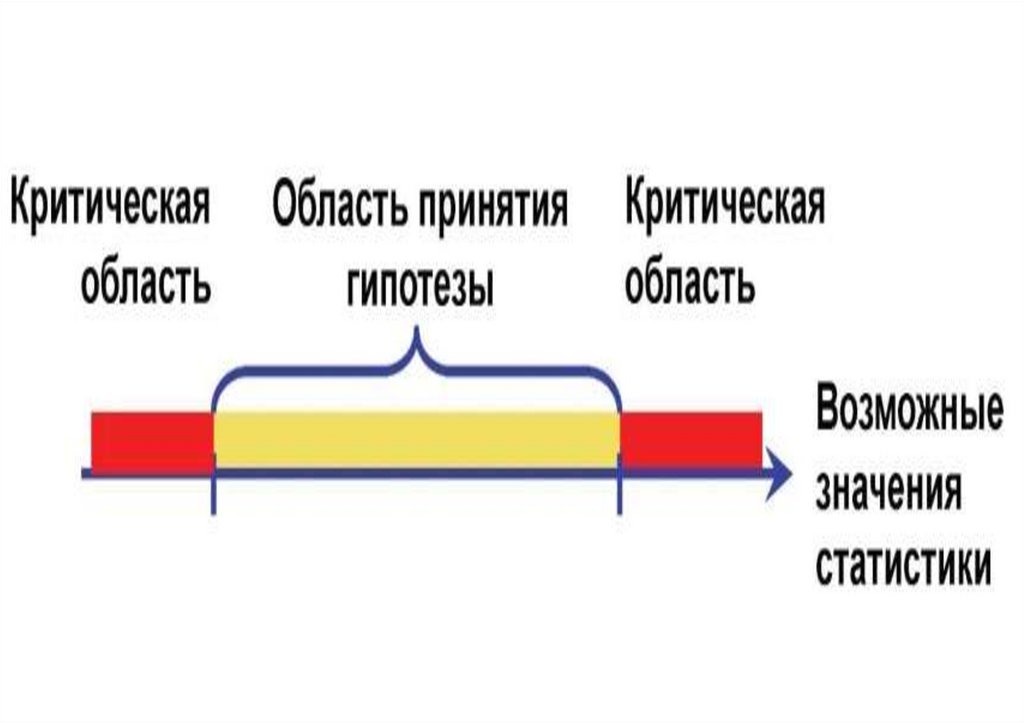
Множество значений статистики включает две области:ОБЛАСТЬ ПРИНЯТИЯ ГИПОТЕЗЫ
множество тех значений статистики, при которых
гипотеза Н0 принимается.
Если значение статистики попало в область принятия
гипотезы, то гипотеза Н0 принимается.
КРИТИЧЕСКАЯ ОБЛАСТЬ ω(α).
множество тех значений статистики, при которых
гипотеза Н0 отклоняется и принимается
альтернативная гипотеза.
Если значение статистики попало в критическую область,
то гипотеза Н0 отклоняется и принимается альтернативная
гипотеза Н1
12.
13.
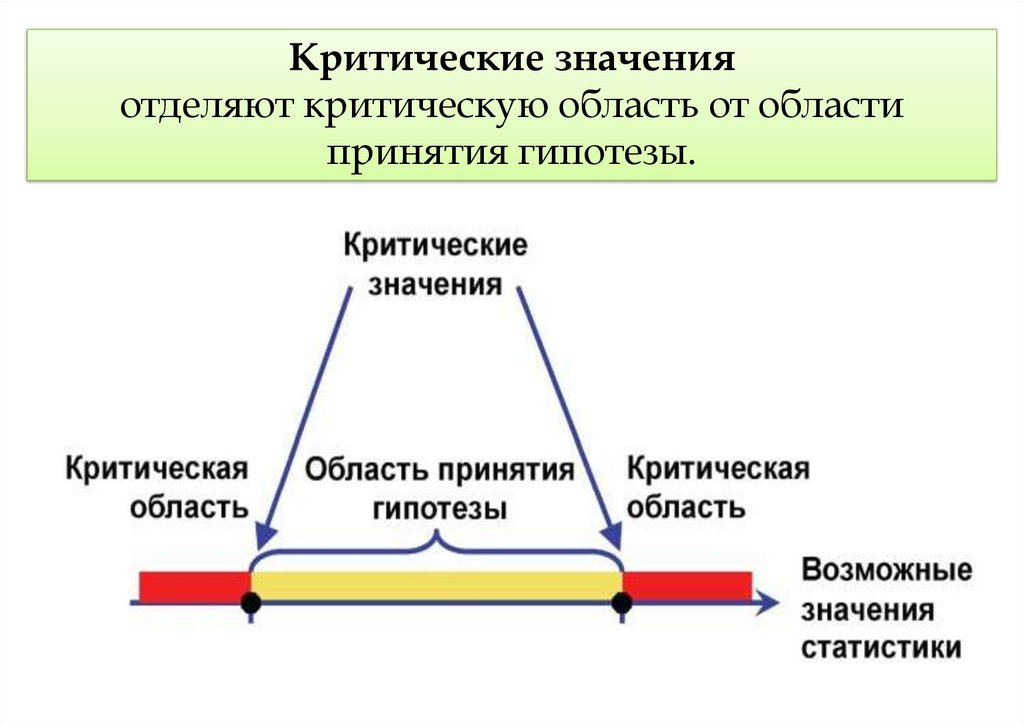
Критические значенияотделяют критическую область от области
принятия гипотезы.
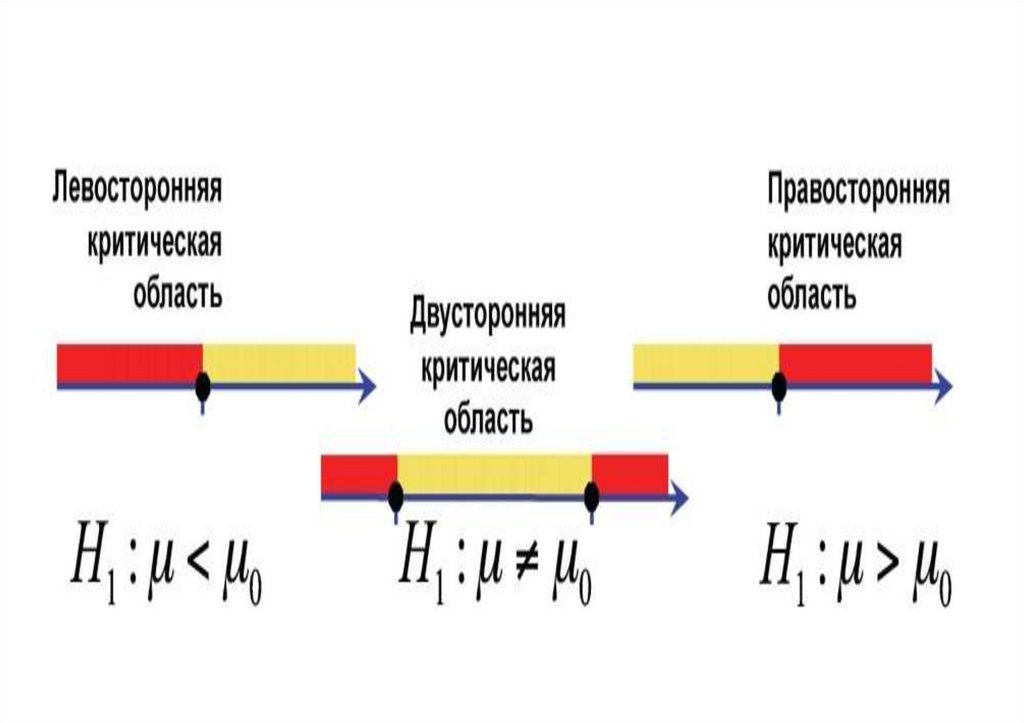
14.
Критическая область строится,исходя из имеющихся знаний о
законе распределения статистики, и
зависит от:
объема выборки,
уровня значимости, задаваемого
исследователем,
вида альтернативной гипотезы.
15.
16.
Алгоритм проверки статистической гипотезы17.
Учебный вопрос №2Проверка гипотезы о
законе распределения
дискретной случайной
величины по критерию
Пирсона
18.
Постановка задачи о проверке гипотезыо виде (законе) распределения
генеральной совокупности
Нередко в приложениях математической
статистики фигурируют задачи, в которых
закон распределения генеральной
совокупности заранее неизвестен, но есть
основания предположить, выдвинуть
гипотезу, что он имеет определённый вид.
19.
H0:Случайная величина X распределена
по нормальному закону с
параметрами : a=5, σ=3
H0:
Случайная величина X распределена
по показательному закону с
параметром = 1,5 .
20.
Критерии, которые используютсядля проверки гипотез о виде
закона распределения,
называются
КРИТЕРИЯМИ
СОГЛАСИЯ
21.
2χ
критерий
(«хи квадрат»))
К. Пирсона
22.
Для дискретных случайных величин покритерию Пирсона сравниваются не
вероятности, а
эмпирические частоты ni (наблюдаемые) и
теоретические n'i частоты (вычисленные в
предположении о правильности гипотезы,
n'i = p i n)
xi
ni
,
ni
x1
n1
,
n1
x2
n2
,
n2
...
...
...
xs
ns
,
ns
23.
Замечание: при пользованиикритерием Пирсона группы с
малочисленными
теоретическими частотами
(для которых n'i 5 ) следует
объединять.
24.
Критерий ПирсонаВеличина, характеризующая отличие
теоретических частот от экспериментальных,
подсчитывается по формуле (статистика
критерия):
2
n i - n i
n i
2
25.
Найдем число степеней свободы k:k=s -r-1
s -количество групп, в вариационном ряду
r -количество параметров распределения,
которые для генеральной совокупности
неизвестны и поэтому их необходимо оценить
по выборке.
26.
Алгоритм проверки гипотезы о законе распределениядискретной случайной величины по критерию Пирсона
1.Выдвинуть гипотезу о законе распределении ДСВ.
2.Найти необходимые точечные оценки.
3.Теоретические частоты распределения найти по формуле ni=pi∙n.
2
4.Определить набл по формуле Пирсона.
5. Рассчитать количество степеней свободы к= s -r-1, где s - число
значений случайной величины в выборке; r- число параметров,
вычисляемых по выборке
кр2
6. Для нахождения
по таблице, необходимо знать уровень
значимости и количество степеней свободы к= s -r-1
7. Найти по таблице
кр2
2
2
8. Сравнить набл . и кр , если:
2
кр2
Х набл
а)
, следовательно, в этом случае гипотезу H0 отвергаем;
>
2
кр
набл
б)
< – гипотезу H0 принимаем.
2

























 Математика
Математика








