Задачи ЕГЭ Многогранники

1.

1

2. Задачи на многогранники

• Вычисление углов
• Вычисление расстояний
• Вычисление площадей
• Вычисление объемов
• Комбинации многогранников и тел
вращения
2

3. Эти замечательные треугольники

Правильный шестиугольник
3

4. Вычисление углов

E1
D1
F1
A1
B1
E
D
F
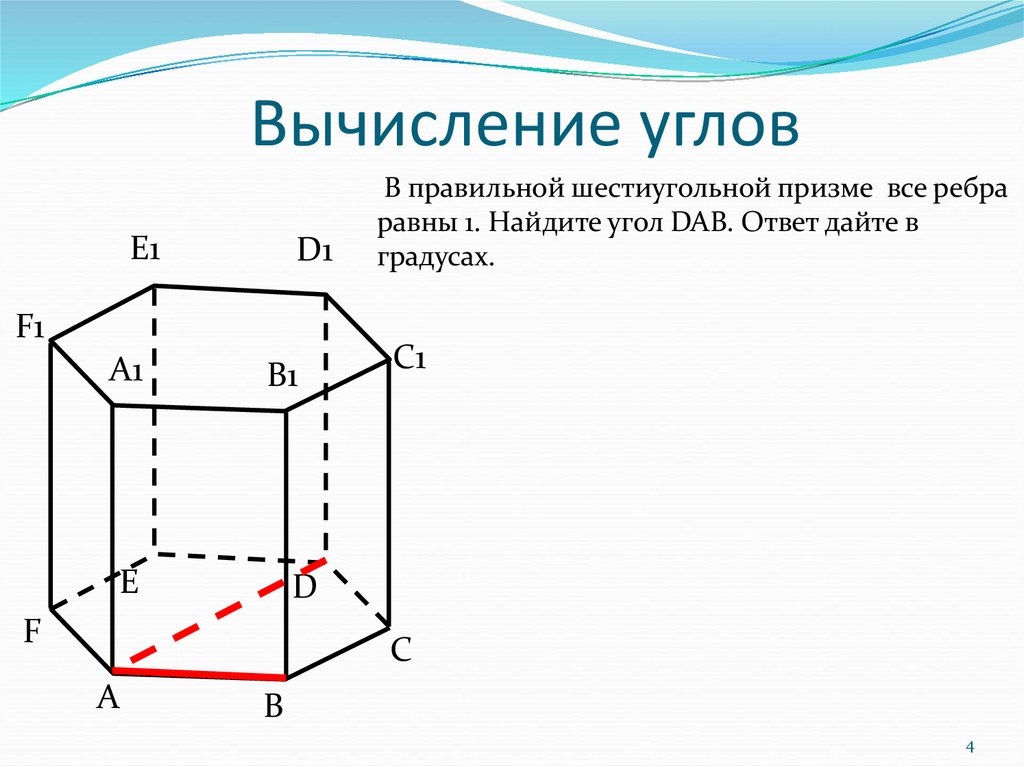
В правильной шестиугольной призме все ребра
равны 1. Найдите угол DAB. Ответ дайте в
градусах.
C1
C
A
B
4

5. Вычисление углов

E1
D1
F1
A1
B1
E
D
F
В правильной шестиугольной призме все ребра
равны 1. Найдите угол DAB. Ответ дайте в
градусах.
C1
C
A
B
5

6. Вычисление углов

• В пространстве существует 4 типа взаимного
расположения прямых: совпадают, пересекаются,
скрещиваются, параллельны.
• угол между прямыми – это такой угол α, что 0⩽α⩽90∘.
• угол между скрещивающимися прямыми равен углу
между пересекающимися параллельными им прямыми
6

7. Вычисление углов

В кубе ABCDA1B1C1D1 точка K лежит на
ребре AA1. Найдите угол между прямыми
D1K и AB. Ответ дайте в градусах.
7

8. Вычисление углов

В кубе ABCDA1 B 1 C 1 D 1 точка K лежит
на ребре AA1. Найдите угол между
прямыми D1K и AB. Ответ дайте в
градусах.
8

9. Вычисление углов

C1
B1
A1
D1
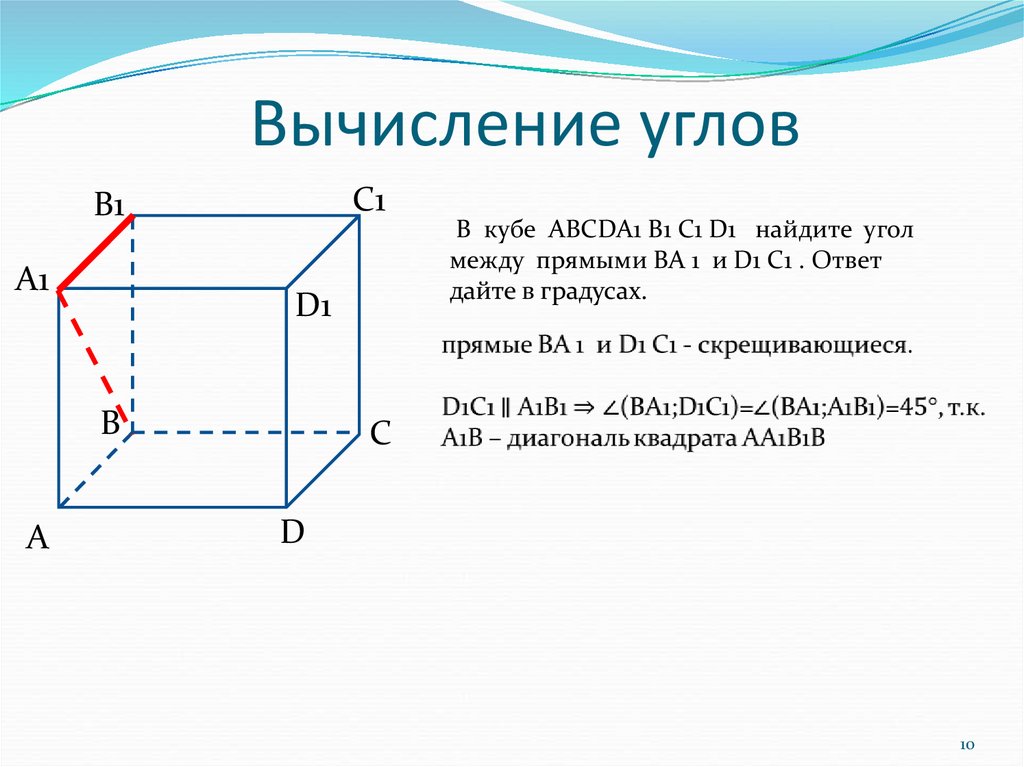
В кубе ABCDA1 B1 C1 D1 найдите угол
между прямыми BA 1 и D1 C1 . Ответ
дайте в градусах.
прямые BA 1 и D1 C1 - скрещивающиеся.
B
A
C
D
9

10. Вычисление углов

C1
B1
A1
D1
B
A
В кубе ABCDA1 B1 C1 D1 найдите угол
между прямыми BA 1 и D1 C1 . Ответ
дайте в градусах.
C
D
10

11. Вычисление углов

C1
B1
A1
D1
B
A
В кубе ABCDA 1 B 1 C 1 D 1 найдите
угол между прямыми CD 1 и BC 1 . Ответ
дайте в градусах.
C
D
11

12. Вычисление углов

C1
B1
A1
D1
B
A
В кубе ABCDA 1 B 1 C 1 D 1 найдите
угол между прямыми CD 1 и BC 1 . Ответ
дайте в градусах.
C
D
12

13. Вычисление углов

C1
B1
A1
D1
B
A
В кубе ABCDA 1 B 1 C 1 D 1 найдите
угол между прямыми CD 1 и BC 1 . Ответ
дайте в градусах.
C
D
13

14. Вычисление углов

D1
A1
C1
B1
D
A
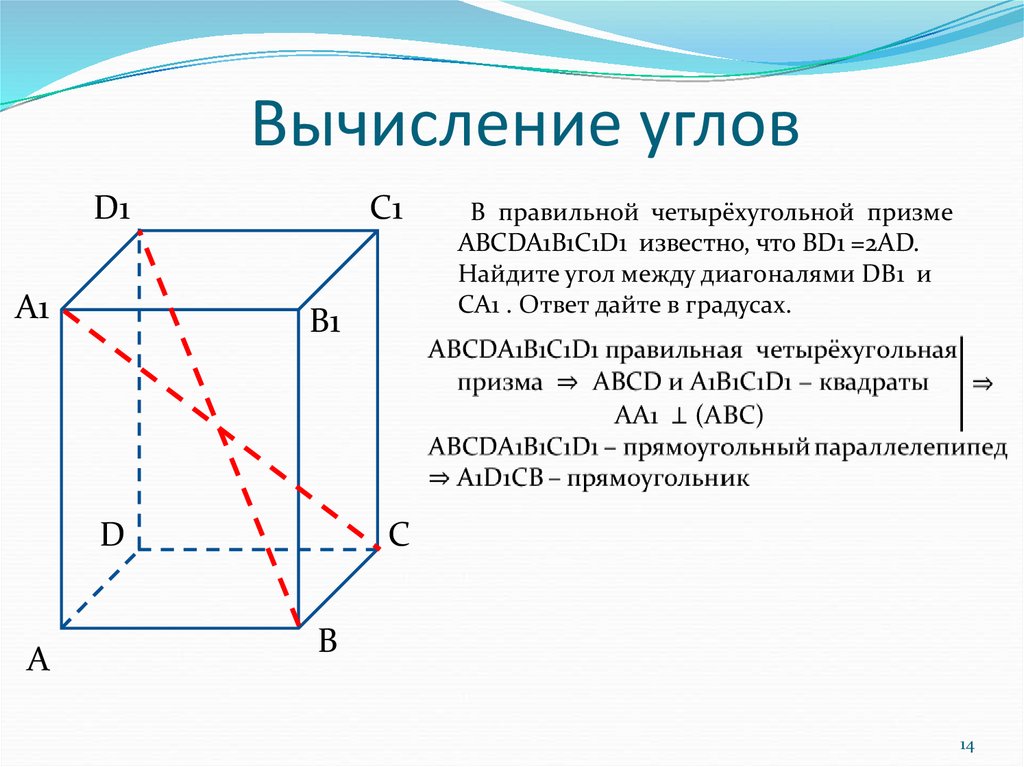
В правильной четырёхугольной призме
ABCDA1B1C1D1 известно, что BD1 =2AD.
Найдите угол между диагоналями DB1 и
CA1 . Ответ дайте в градусах.
C
B
14

15. Вычисление углов

D1
A1
C1
B1
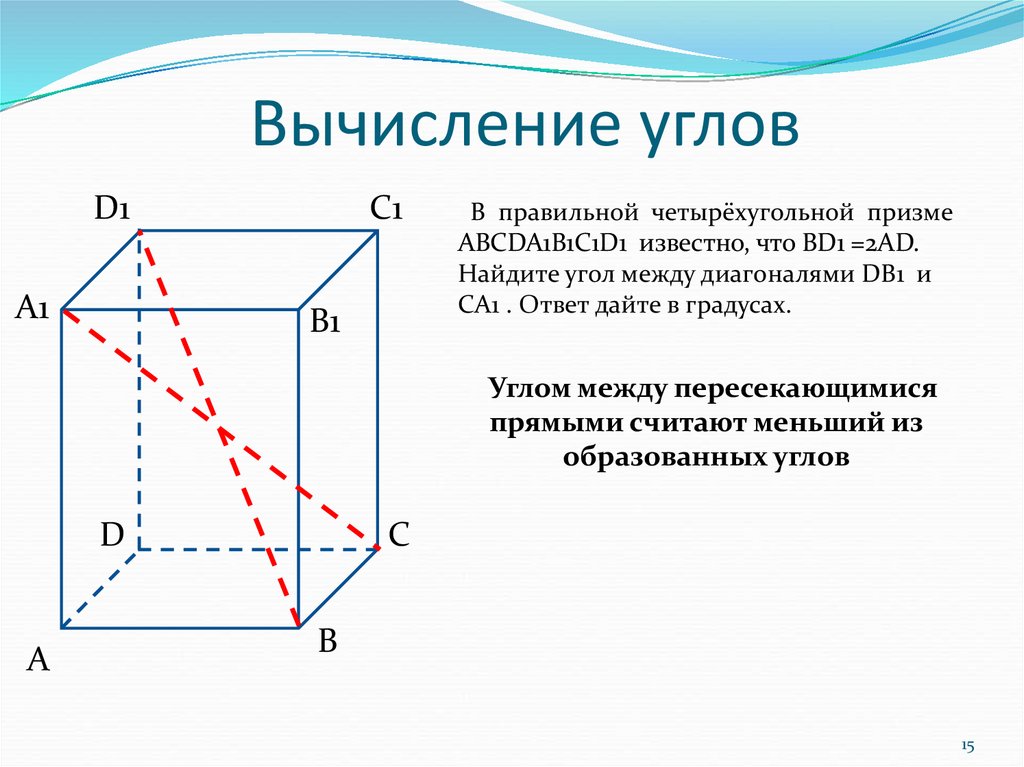
В правильной четырёхугольной призме
ABCDA1B1C1D1 известно, что BD1 =2AD.
Найдите угол между диагоналями DB1 и
CA1 . Ответ дайте в градусах.
Углом между пересекающимися
прямыми считают меньший из
образованных углов
D
A
C
B
15

16. Вычисление углов

D1
A1
C1
B1
D
A
В правильной четырёхугольной призме
ABCDA1B1C1D1 известно, что BD1 =2AD.
Найдите угол между диагоналями DB1 и
CA1 . Ответ дайте в градусах.
C
B
16

17. Вычисление углов

D1
A1
C1
B1
D
A
В правильной четырёхугольной призме
ABCDA1B1C1D1 известно, что BD1 =2AD.
Найдите угол между диагоналями DB1 и
CA1 . Ответ дайте в градусах.
C
D1
C
A1
B
B
17

18. Вычисление углов

D1
A1
C1
B1
D
A
В правильной четырёхугольной призме
ABCDA1B1C1D1 известно, что BD1 =2AD.
Найдите угол между диагоналями DB1 и
CA1 . Ответ дайте в градусах.
C
D1
C
О
B
A1
B
18

19. Вычисление углов

C1
B1
D1
A1
F1
C
D
B
E1
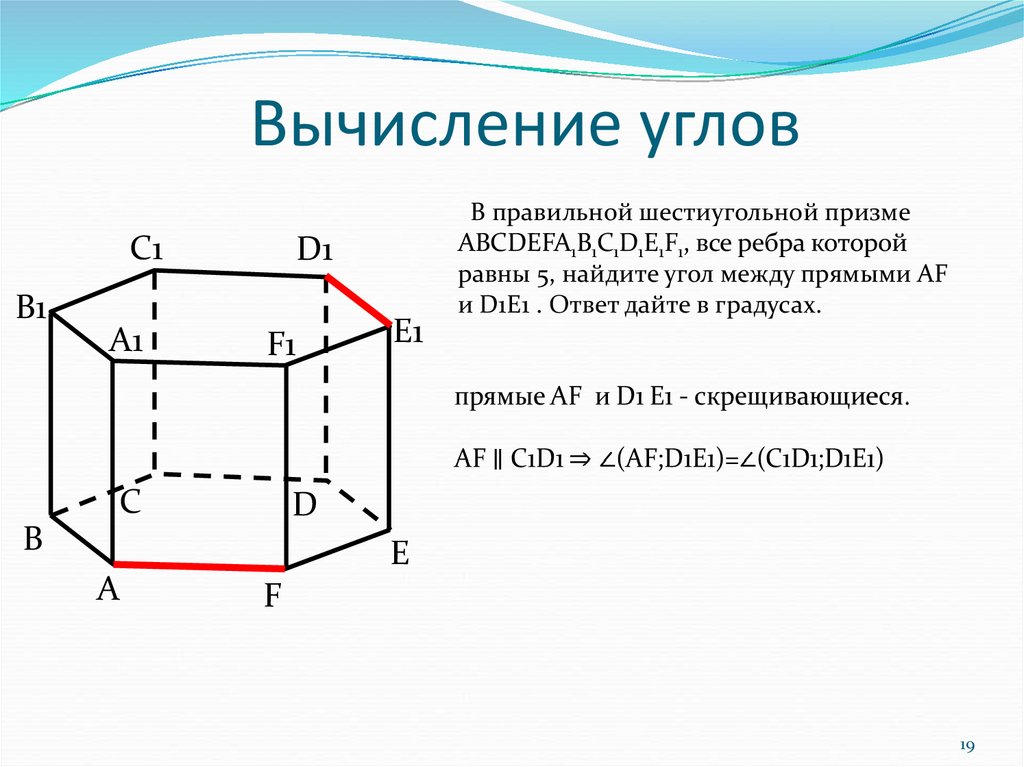
В правильной шестиугольной призме
АВСDEFA1B1C1D1E1F1, все ребра которой
равны 5, найдите угол между прямыми AF
и D1E1 . Ответ дайте в градусах.
E
A
F
19

20. Вычисление углов

C1
B1
D1
A1
F1
C
D
B
E1
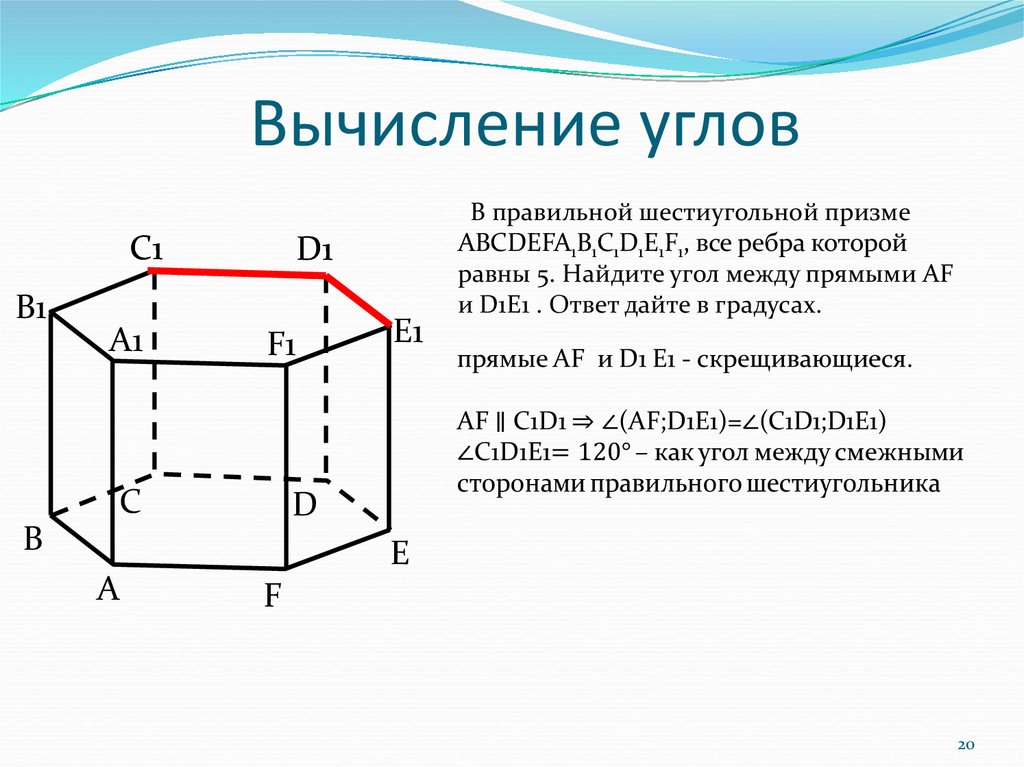
В правильной шестиугольной призме
АВСDEFA1B1C1D1E1F1, все ребра которой
равны 5. Найдите угол между прямыми AF
и D1E1 . Ответ дайте в градусах.
E
A
F
20

21. Вычисление углов

C1
B1
D1
A1
F1
C
D
B
E1
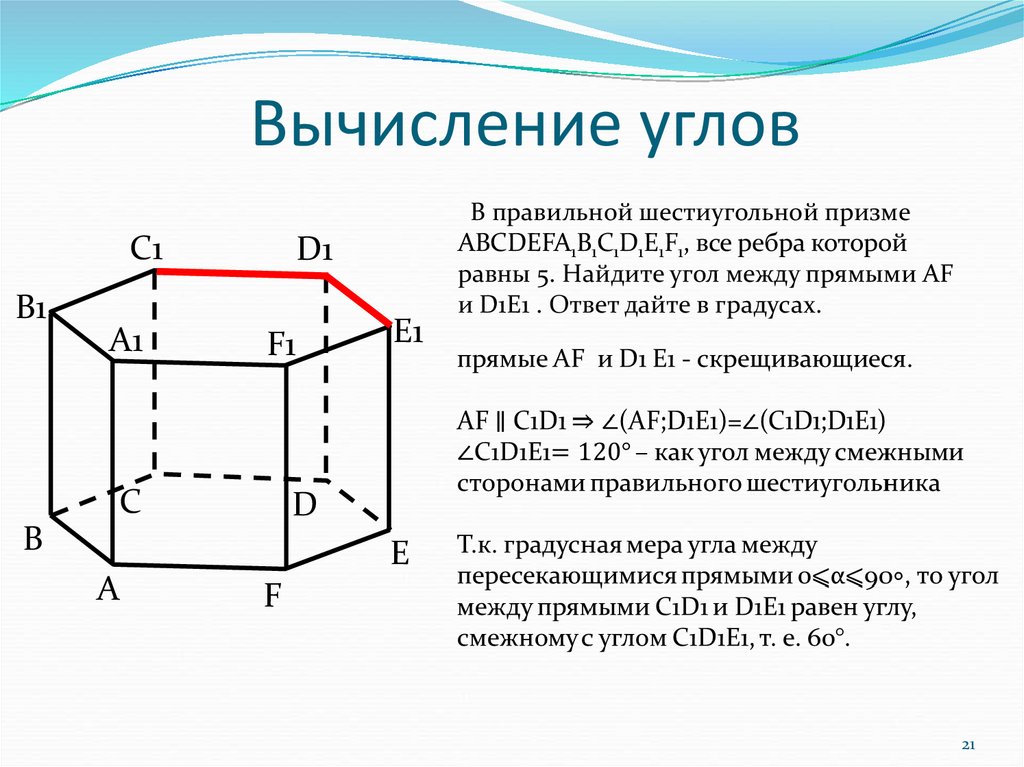
В правильной шестиугольной призме
АВСDEFA1B1C1D1E1F1, все ребра которой
равны 5. Найдите угол между прямыми AF
и D1E1 . Ответ дайте в градусах.
E
A
F
21

22. Вычисление расстояний

• Вычисление расстояний между точками
• Вычисление элементов многогранников
22

23. Вычисление расстояний

На рисунке изображён многогранник, все
двугранные углы многогранника прямые.
Найдите квадрат расстояния между
вершинами B и D2 .
A
B
23

24. Вычисление расстояний

На рисунке изображён многогранник, все
двугранные углы многогранника прямые.
Найдите квадрат расстояния между
вершинами B и D2 .
Квадрат диагонали прямоугольного
параллелепипеда равна сумме
квадратов трех его измерений
d2 = a2 + b2 + c2
A
B
24

25. Вычисление площадей

• Площадь полной поверхности
• Площадь боковой поверхности
• Площадь сечения
25

26. Вычисление площадей

Найдите площадь поверхности
многогранника, изображенного на
рисунке (все двугранные углы прямые).
Прием «Я и моя тень»
S=(Вид спереди +вид сбоку + вид сверху)*2
26

27. Вычисление площадей

Найдите площадь поверхности
многогранника, изображенного на
рисунке (все двугранные углы прямые).
27

28. Вычисление площадей

Найдите площадь поверхности
многогранника, изображенного на
рисунке (все двугранные углы прямые).
3
2
6
7
28

29. Вычисление площадей

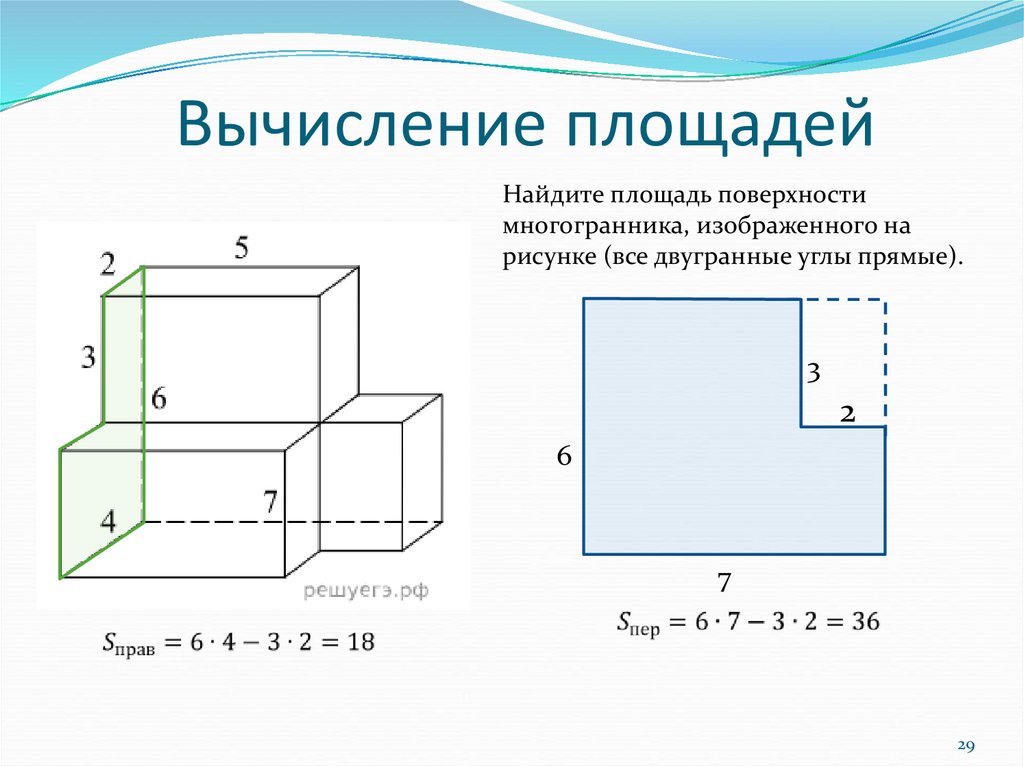
Найдите площадь поверхности
многогранника, изображенного на
рисунке (все двугранные углы прямые).
3
2
6
7
29

30. Вычисление площадей

Найдите площадь поверхности
многогранника, изображенного на
рисунке (все двугранные углы прямые).
3
2
6
7
30

31. Вычисление площадей

Найдите площадь поверхности
многогранника, изображенного на
рисунке (все двугранные углы прямые).
3
2
6
7
31

32. Вычисление площадей

Найдите площадь поверхности
пространственного креста, изображенного на
рисунке и составленного из единичных кубов.
Вид спереди = вид сбоку = вид сверху
32

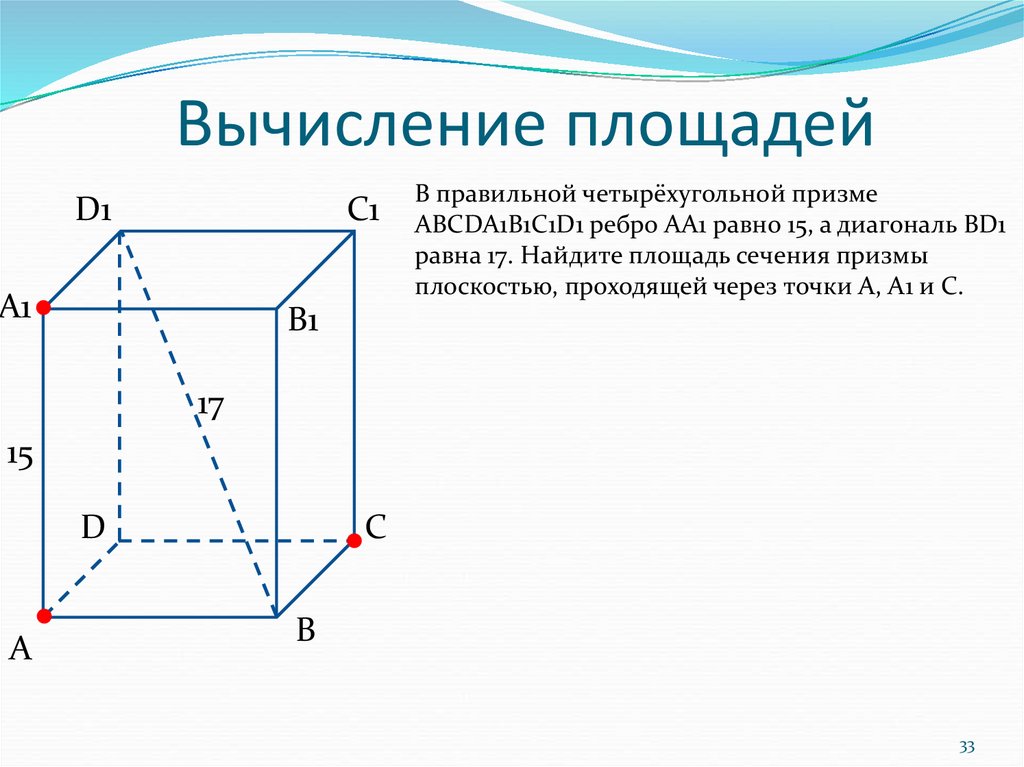
33. Вычисление площадей

D1
C1
A1
В правильной четырёхугольной призме
ABCDA1B1C1D1 ребро AA1 равно 15, а диагональ BD1
равна 17. Найдите площадь сечения призмы
плоскостью, проходящей через точки A, A1 и C.
B1
17
15
D
A
C
B
33

34. Вычисление площадей

D1
C1
A1
В правильной четырёхугольной призме
ABCDA1B1C1D1 ребро AA1 равно 15, а диагональ BD1
равна 17. Найдите площадь сечения призмы
плоскостью, проходящей через точки A, A1 и C.
B1
17
15
D
A
C
B
34

35. Вычисление объемов

• Объем многогранника
• Объем части многогранника
35

36. Это полезно знать

Если все линейные размеры многогранника увеличить(уменьшить) в
k раз, то получится многогранник подобный данному.
Коэффициент подобия равен отношению сходственных линейных
элементов этих многогранников.
Прямо пропорциональная зависимость
величин
36

37. Это полезно знать

Если изменяются не все линейные размеры многогранника, а только
некоторые элементы, применяй правило:
«Если один из множителей увеличивается (уменьшается)в
несколько раз, то произведение увеличивается(уменьшается) во
столько же раз.»
Рассмотрим произведение нескольких множителей
37

38. Вычисление объемов

Во сколько раз увеличится объем октаэдра, если
все его ребра увеличить в 4 раза?
Во сколько раз увеличится площадь поверхности
октаэдра, если все его ребра увеличить в 4 раза?
38

39. Вычисление объемов

Во сколько раз увеличится объем пирамиды, если
ее высоту увеличить в четыре раза?
O
39

40. Вычисление объемов

40

41. Вычисление объемов

Объем треугольной пирамиды SAFE, являющейся
частью правильной шестиугольной пирамиды SABCDEF,
равен 8. Найдите объем шестиугольной пирамиды.
Высота у шестиугольной пирамиды и треугольной
общая.
O
41

42. Вычисление объемов

Объем треугольной пирамиды SAFE, являющейся
частью правильной шестиугольной пирамиды SABCDEF,
равен 8. Найдите объем шестиугольной пирамиды.
O
42

43. Вычисление объемов

Объем треугольной пирамиды SAFE, являющейся
частью правильной шестиугольной пирамиды SABCDEF,
равен 8. Найдите объем шестиугольной пирамиды.
O
S
43

44. Вычисление объемов

Объем правильной треугольной призмы равен 6. Каким
будет объем призмы, если стороны ее основания
увеличить в 3 раза, а высоту уменьшить в 2 раза.
Уменьшим высоту призмы в 2 раза.
44

45. Вычисление объемов

Объем правильной треугольной призмы равен 6. Каким
будет объем призмы, если стороны ее основания
увеличить в 3 раза, а высоту уменьшить в 2 раза.
в 2 раза
в 2 раза
Увеличим стороны основания призмы
в 3 раза.
45

46. Вычисление объемов

Объем правильной треугольной призмы равен 6. Каким
будет объем призмы, если стороны ее основания
увеличить в 3 раза, а высоту уменьшить в 2 раза.
в 2 раза
3
в 2 раза
Площадь основания и объем - прямо
пропорциональные величины.
Найдем во сколько раз увеличится
площадь основания
Значит, объем призмы увеличится в 9 раз.
46

47. Вычисление объемов

Объем правильной треугольной призмы равен 6. Каким
будет объем призмы, если стороны ее основания
увеличить в 3 раза, а высоту уменьшить в 2 раза.
в 2 раза
3
в 2 раза
Площадь основания и объем - прямо
пропорциональные величины.
Найдем во сколько раз увеличится
площадь основания
47

48. Вычисление объемов

Через среднюю линию основания треугольной призмы,
объем которой равен 32, проведена плоскость,
параллельная боковому ребру. Найдите объем
отсеченной треугольной призмы.
Высоты начальной и отсеченной
призмы – одинаковые. Основания –
подобные треугольники.
Найдем во сколько раз уменьшилась
площадь основания
48

49. Вычисление объемов

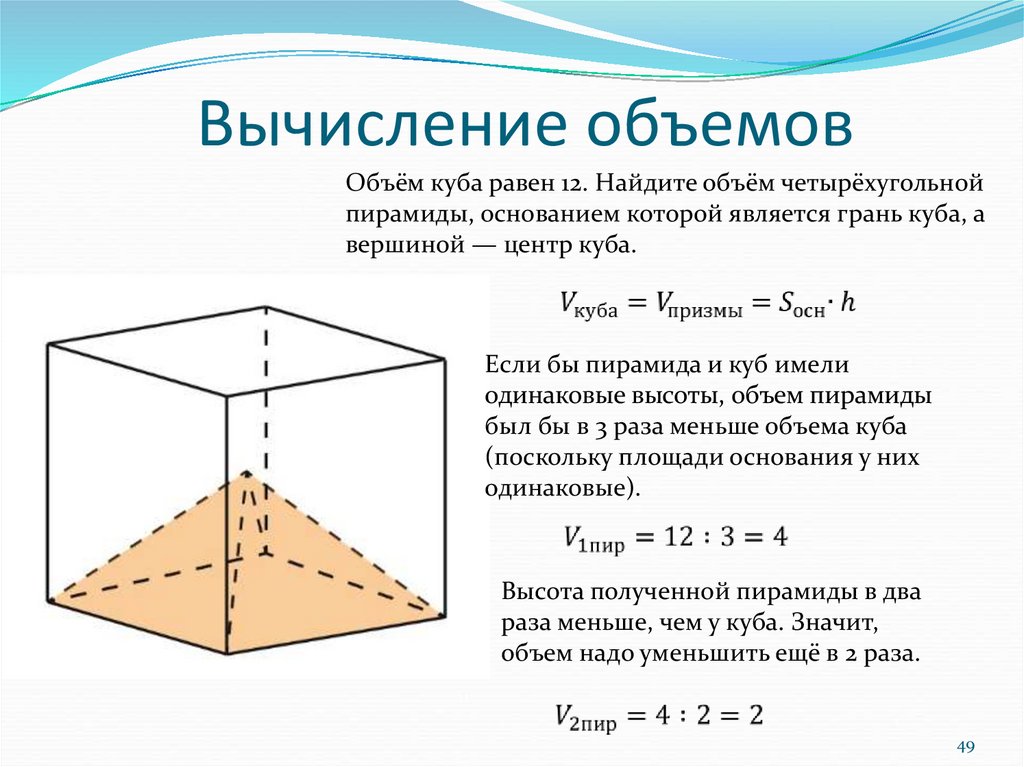
Объём куба равен 12. Найдите объём четырёхугольной
пирамиды, основанием которой является грань куба, а
вершиной — центр куба.
Если бы пирамида и куб имели
одинаковые высоты, объем пирамиды
был бы в 3 раза меньше объема куба
(поскольку площади основания у них
одинаковые).
Высота полученной пирамиды в два
раза меньше, чем у куба. Значит,
объем надо уменьшить ещё в 2 раза.
49

50. Вычисление объемов

Объём куба равен 12. Найдите объём четырёхугольной
пирамиды, основанием которой является грань куба, а
вершиной — центр куба.
Посчитаем, сколько нужно таких
четырёхугольных пирамидок, чтобы
сложить из них этот куб.
Их 6, так как у куба 6 граней.
50

51. Вычисление объемов

51

52. Комбинации тел

52

53. Комбинации тел

Вынесем на плоскость вид сверху
53

54. Комбинации тел

Вынесем на плоскость вид сверху
54

55. Комбинации тел

55

56. Комбинации тел

Вынесем на плоскость описанный правильный
шестиугольник
56

57. Используемые материалы

• https://ege.sdamgia.ru/get_file?id=29693
• https://ege.sdamgia.ru/get_file?id=29695
• https://ege.sdamgia.ru/get_file?id=29887
• https://ege.sdamgia.ru/get_file?id=113238
• https://ege-study.ru/wp-content/uploads/2022/11/6-3.jpg
• https://ege-study.ru/wp-content/uploads/2012/08/stereo_2_182.png
• https://ege.sdamgia.ru/get_file?id=29782
57