Похожие презентации:
Метрики эффективности
1.
МЕТРИКИ ЭФФЕКТИВНОСТИ2.
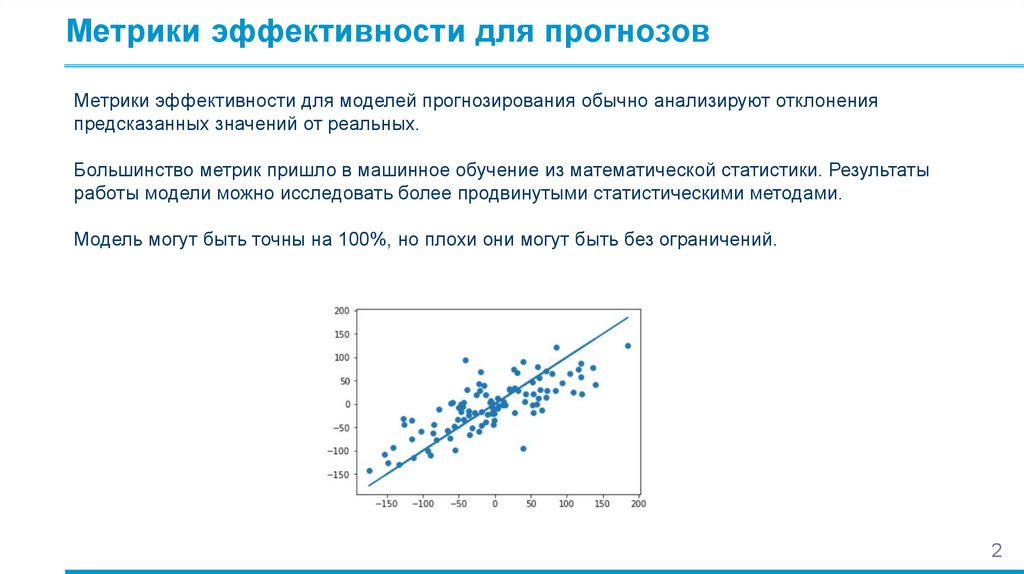
Метрики эффективности для прогнозовМетрики эффективности для моделей прогнозирования обычно анализируют отклонения
предсказанных значений от реальных.
Большинство метрик пришло в машинное обучение из математической статистики. Результаты
работы модели можно исследовать более продвинутыми статистическими методами.
Модель могут быть точны на 100%, но плохи они могут быть без ограничений.
2
3.
Коэффициент детерминации (r-квадрат)где
- вектор эмпирических (истинных) значений целевой переменной,
вектор теоретических (предсказанных) значений целевой переменной,
эмпирическое значение целевой переменной для i-го объекта,
теоретическое значение целевой переменной для i-го объекта,
среднее из эмпирических значений целевой переменной для i-го объекта
3
4.
Коэффициент детерминации (r-квадрат)Коэффициент детерминации показывает силу связи между двумя случайными величинами.
Если модель всегда предсказывает точно, метрика равна 1. Для тривиальной модели - 0.
Несимметричная метрика эффективности.
Эта метрика не определена, если целевая функция не меняет своих значений
4
5.
Средняя абсолютная ошибка (MAE)Средняя абсолютная ошибка (mean absolute error, MAE) - средняя величина разницы между
предсказанными и реальными значениями целевой функции
MAE показывает среднее абсолютное отклонение предсказанных значений от реальных
Чем выше значение MAE, тем модель хуже. У идеальной модели MAE = 0
MAE очень легко интерпретировать: на сколько в среднем ошибается модель
5
6.
Средний квадрат ошибки (MSE)Средний квадрат ошибки (mean squared error, MSE)
MAE показывает средний квадрат отклонений предсказанных значений от реальных
Чем выше значение MSE, тем модель хуже. У идеальной модели MSE = 0
MSE больше учитывает сильные отклонения, но хуже интерпретируется, чем MAE, чувствительна к
аномалиям и выбросам
6
7.
Среднеквадратичная ошибка (RMSE)Среднеквадратичная ошибка (root mean squared error, RMSE)
RMSE - это корень из MSE. Выражается в тех же единицах, что и целевая переменная
Чаще применяется при статистическом анализе данных
Чувствительна к аномалиям и выбросам
7
8.
Среднеквадратичная логарифмическая ошибка (MSLE)Среднеквадратическая логарифмическая ошибка (mean squared logarithmic error, MSLE)
MSLE это среднее отклонение логарифмов реальных и предсказанных данных
У идеальной модели MSLE = 0
Используется при большом интервале варьирования значений целевой функции (разных масштабах)
Полезна, если моделируется процесс в экспоненциальным ростом
8
9.
Среднее процентное отклонение (MAPE)Средняя абсолютная процентная ошибка (mean absolute percentage error, MAPE)
Идея метрики - чувствительность к относительным отклонениям
Метрика выражается в процентах и имеет хорошую интерпретируемость
Идеальная модель имеет MAPE = 0. Верхний предел - не ограничен
Отдает предпочтение предсказанию меньших значений
В русскоязычной литературе называется относительной ошибкой, так как она учитывает отклонение относительно целевого
значения. В англоязычной литературе метрика называется абсолютной из-за модуля
9
10.
Абсолютная медианная ошибкаМедианная абсолютная ошибка (median absolute error, MedAE)
Медианная абсолютная ошибка похожа на среднюю абсолютную, но более устойчива к аномалиям
Применяется в задачах, когда известно, что в данных присутствуют выбросы, аномальные ,
непоказательные значения
Эта метрика более робастная, нежели MAE
10
11.
Максимальная ошибка (ME)Максимальная ошибка (maximum error, ME) - величина максимального абсолютного отклонения
предсказанных значений от теоретических
Максимальная ошибка показывает наихудший случай предсказания модели и не характеризует
распределение отклонений
В некоторых задачах важно, чтобы модель не ошибалась сильно, а небольшие отклонения не
критичны
Используется как вспомогательная совместно с другими метриками качества модели
11
12.
Метрики эффективности для классификацийЦелевые переменные, которые существуют в задачах классификации обычно не обладают
свойством порядка в значениях целевой переменной, когда целевая функция измеряется по
относительной шкалею
Имеет значение только разница между правильным предсказанием и неправильным, поэтому
метрики эффективности для классификации оценивают количество правильно и неправильно
классифицированных (распознанных) объектов
В задачах классификации почти всегда надо применять несколько метрик одновременно
Вообще, чем больше в задаче классов, тем ниже ожидаемые значения эффективности. Поэтому
качество бинарной классификации при прочих равных почти всегда выше, чем для множественной
Метрики эффективности классификации не позволяют сопоставить задачи, состоящие из разного
количества классов
12
13.
Доля правильных ответов (accuracy)Подсчитывается как количество объектов в выборке, которые были классифицированы правильно,
разделенное на общее количество объектов выборки
Индикаторная (характеристическая) функция - это функция, определенная на наборе X, которая
указывает принадлежность элемента к подмножеству A из X, имеющий значение 1 для всех
элементов A и значение 0 для всех элементов X не в A.
Точность (accuracy) - самая простая метрика качества классификации, доля правильных ответов.
Может быть выражена в процентах или в долях
Метрика точности очень чувствительная к несбалансированности классов (когда объекты очень
неравномерно распределены по классам)
13
14.
Метрики классификации для неравных классовИстинно положительные (true positive, TP) - это те объекты, которые отнесены моделью к
положительному классу и действительно ему принадлежат
Истинно отрицательные (true negative, TN) - соответственно те, которые правильно распознаны
моделью как принадлежащие отрицательному классу
Ложноположительные объекты (FP, false positive) - это те, которые модель распознала как
положительные, хотя на самом деле они отрицательные (ошибка первого рода)
Ложноотрицательные значения (false negative, FN) - это те, которые ошибочно отнесены моделью к
отрицательному классу, хотя на самом деле они принадлежат положительному (ошибка второго
рода)
14
15.
Метрики классификации для неравных классовТочность A (accuracy) – доля истинно положительных и истинно отрицательных среди всех случаев
(симметричная мера)
Точность P (precision) - доля объектов, правильно распознанных как положительные из всех,
распознанных как положительные (характеризует способность модели отличать положительный
класс от отрицательного, не делать ложноположительных предсказаний):
Полнота R (recall) - доля положительных объектов выборки, распознанных моделью (будет равна 1
только в том случае, если модель не делает ошибок второго рода):
15
16.
Метрика F1Какая модель лучше: с большим precision или recall?
Метрика F1 подразумевает, что нам одинаково важны точность и полнота:
Если одна из этих метрик важнее, используют обобщение метрики F1 - семейство F-метрик:
Эта метрика имеет параметр
который определяет, во сколько раз recall важнее precision.
Если этот параметр больше единицы, то метрика будет полагать recall более важным. А если
меньше - то важнее будет precision. При
мы получим метрику F1.
Все метрики из F-семейства измеряются от 0 до 1: чем значение больше, тем модель лучше
16
17.
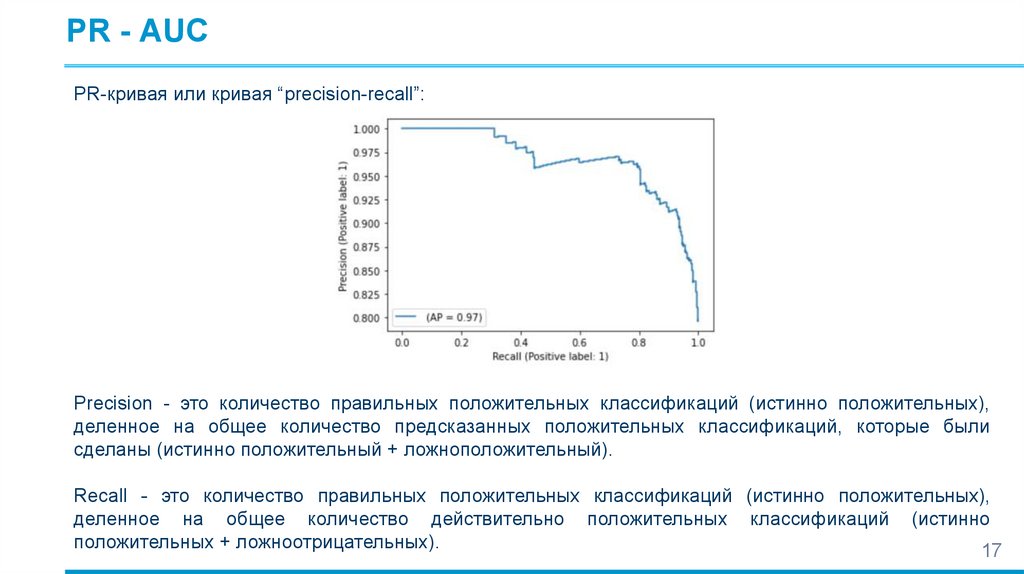
PR - AUCPR-кривая или кривая “precision-recall”:
Precision - это количество правильных положительных классификаций (истинно положительных),
деленное на общее количество предсказанных положительных классификаций, которые были
сделаны (истинно положительный + ложноположительный).
Recall - это количество правильных положительных классификаций (истинно положительных),
деленное на общее количество действительно положительных классификаций (истинно
положительных + ложноотрицательных).
17
18.
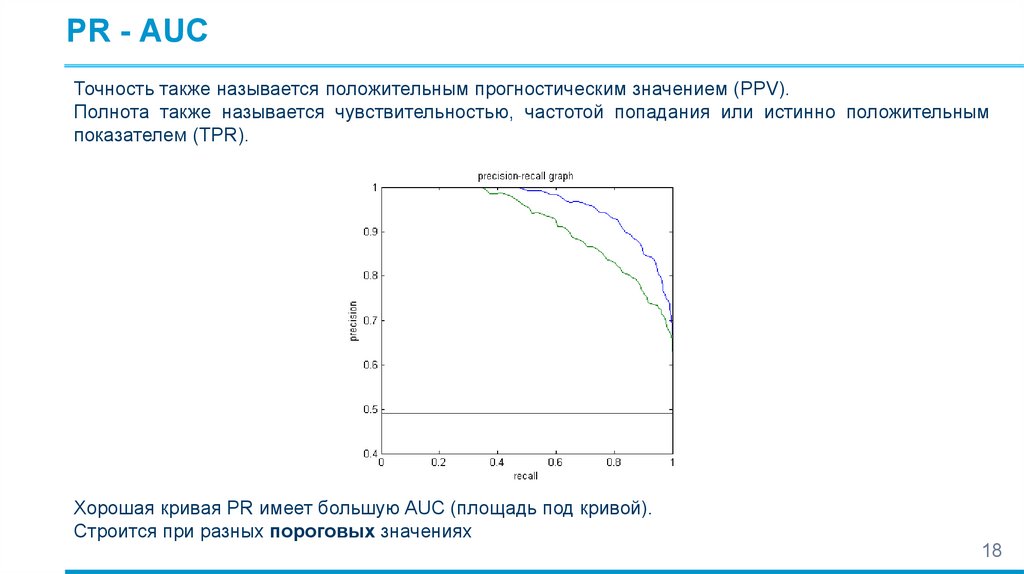
PR - AUCТочность также называется положительным прогностическим значением (PPV).
Полнота также называется чувствительностью, частотой попадания или истинно положительным
показателем (TPR).
Хорошая кривая PR имеет большую AUC (площадь под кривой).
Строится при разных пороговых значениях
18
19.
PR - AUCКривая precision-recall используется для методов метрической классификации, которые выдают
вероятность принадлежности объекта данному классу
Дискретная классификации производится при помощи порогового значения. Чем больше порог, тем
больше объектов модель будет относить к отрицательному классу
Повышение порога в среднем увеличивает precision модели, но понижает recall
PR-кривая может использоваться для выбора оптимальное значение порога.
PR-кривая нужна для того, чтобы сравнивать и оценивать модели вне зависимости от выбранного
уровня порога
PR-AUC - площадь под PR-кривой: у лучшей модели - 1.0, у худшей - 0.0
19
20.
PR – AUC. ПримерПри заданном пороге:
TP = Документ был классифицирован как
“Спортивный” и на самом деле был ”Спортивным".
D1, D2, D10 и D11 соответствуют TP.
TN = Документ был классифицирован как “Не
спортивный” и на самом деле был ”Не спортивным".
D5, D8 и D9 соответствуют TN.
FP = Документ был классифицирован как
“Спортивный”, но на самом деле был “Не
спортивным”. D3 и D7 соответствуют FP.
FN = Документ был классифицирован как “Не
спортивный”, но на самом деле был ”Спортивным".
D4, D6 и D12 соответствуют FN.
Таким образом, TP = 4, TN = 3, FP = 2 и FN = 3.
Отсюда:
точность = TP /(TP + FP) = 4/6 = 2/3
полнота = TP / (TP + FN) = 4/7.
Ставим эту точку на графике. Затем меняем порог
20
21.
ROC - AUCROC-кривая (receiver operating characteristic) - это график показывающий соотношение доли истинно
положительных предсказаний и ложноположительных предсказаний
Доля истинно положительных предсказаний (TPR, true positive rate) - это отношение количества
объектов выборки, правильно распознанных как положительные, ко всем положительным объектам
(метрика recall).
Доля ложноположительных предсказаний (FPR, false positive rate) – это отношение количества
отрицательных объектов, неправильно распознанных как положительные, в общем количестве
отрицательных объектов выборки.
FPR - мера ошибки модели. То есть, чем больше FPR - тем хуже модель. У идеальной модели
FRP=0, а у наихудшей - FPR=1
21
22.
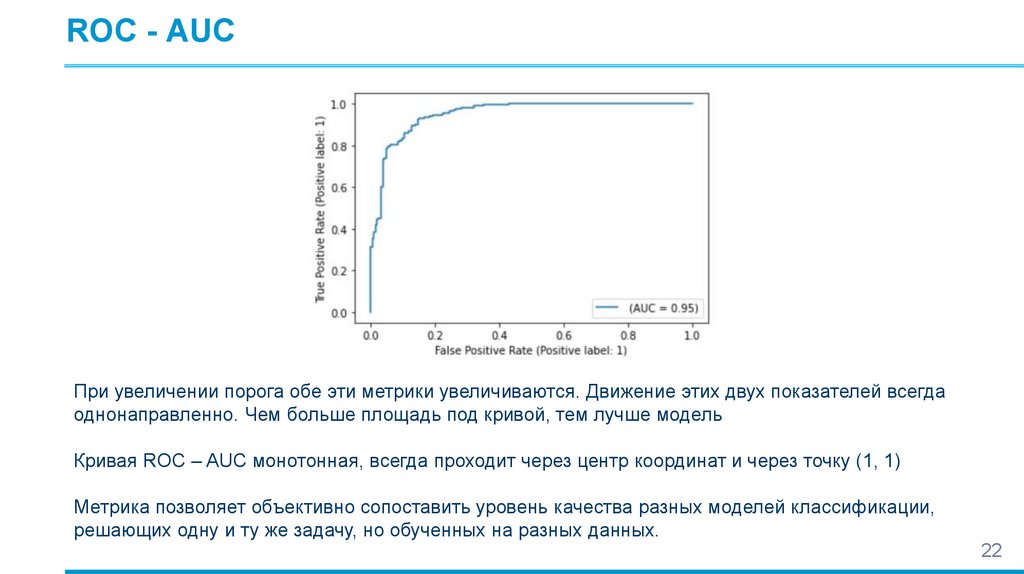
ROC - AUCПри увеличении порога обе эти метрики увеличиваются. Движение этих двух показателей всегда
однонаправленно. Чем больше площадь под кривой, тем лучше модель
Кривая ROC – AUC монотонная, всегда проходит через центр координат и через точку (1, 1)
Метрика позволяет объективно сопоставить уровень качества разных моделей классификации,
решающих одну и ту же задачу, но обученных на разных данных.
22
23.
Индекс силуэтаИндекс силуэта, коэффициент силуэта (Silhouette index, Silhouette coefficient) – мера качества
разбиения на кластеры
Показывает, насколько каждый объект «похож» на другие объекты в том кластере, в который он был
распределён в процессе кластеризации, и «не похож» на объекты из других кластеров
Для каждого i-го наблюдения из кластера C(I) можно вычислить среднее расстояние между i-м и
остальными j-ми объектами кластера:
где |C(I)| — мощность I-го кластера (т.е. число попавших в него объектов), d(i,j) — расстояние между
объектами i и j кластера I. Усреднение производится по |C(I)|−1 объектам, поскольку
расстояние d(i,i) учитывать смысла нет
Можно интерпретировать a(i) как меру того, с какой степенью уверенности объект i может быть
отнесён к кластеру, т.е. насколько он «похож» на остальные объекты этого же кластера
23
24.
Индекс силуэтаДля каждого наблюдения i из C(I) можно определить:
где j ∈ C(J) — объект, содержащийся в любом кластере C(J), отличном от C(I).
Это будет наименьшим средним расстоянием от i до всех точек в любом другом кластере, который
не содержит i. Кластер с наименьшим b(i) называют соседним для i поскольку он является
следующим предпочтительным кластером для этого объекта.
Теперь определим значение коэффициента силуэта s(i) для отдельного объекта i:
при условии, что |C(I)|>1. В то же время s(i)=0, если |C(I)|=1
24
25.
Индекс силуэтаЗначение s(i) близкое к 1 означает, что данные кластеризованы хорошо, т.е. объекты «похожи» друг
на друга внутри кластеров, и не похожи на объекты соседних кластеров (в среднем,
внутрикластерные расстояния меньше междукластерных)
Если s(i) близко к -1, то в соответствии с той же логикой, можно предположить, что объект i более
подходит к соседним кластерам, чем к тому, в который он был распределён при кластеризации
Значение s(i) близкое к 0 говорит о том, что объект расположен вблизи границы кластеров и высокой
уверенности в его принадлежности нет
Вычислив
s(i)
для всех наблюдений в кластере, можно увидеть насколько плотно они
сгруппированы вокруг его центра
Рассчитав среднее значение s(i) по всем кластерам, можно сделать вывод, о том, насколько
сформированная кластерная структура соответствует естественной группировке данных.
Если кластеров больше или меньше, чем естественных групп данных, то силуэты некоторых
кластеров будут значительно «уже» остальных
https://wiki.loginom.ru/articles/cluster-silhouette-index.html
25





















 Математика
Математика








