Обработка естественного языка и компьютерное зрение. Полиномиальная регрессия. Переобучение. Метрики регрессии

1.

Обработка естественного
языка и компьютерное зрение
Полиномиальная регрессия.
Переобучение. Метрики
регрессии.
Черепанов Н.А. МИДиС
10.09.2024

2.

Полиномиальная регрессия
Хорошая
модель
Зарплата
• Модель линейной регрессии не может
точно отразить истинную взаимосвязь
между заработной платой и # годами
опыта.
Модель линейной
регрессии
Обучающий датасет
Опыт работы

3.

BIAS
AND VARIANCE:
INTUITION
Полиномиальная
регрессия
Модель
Зарплата
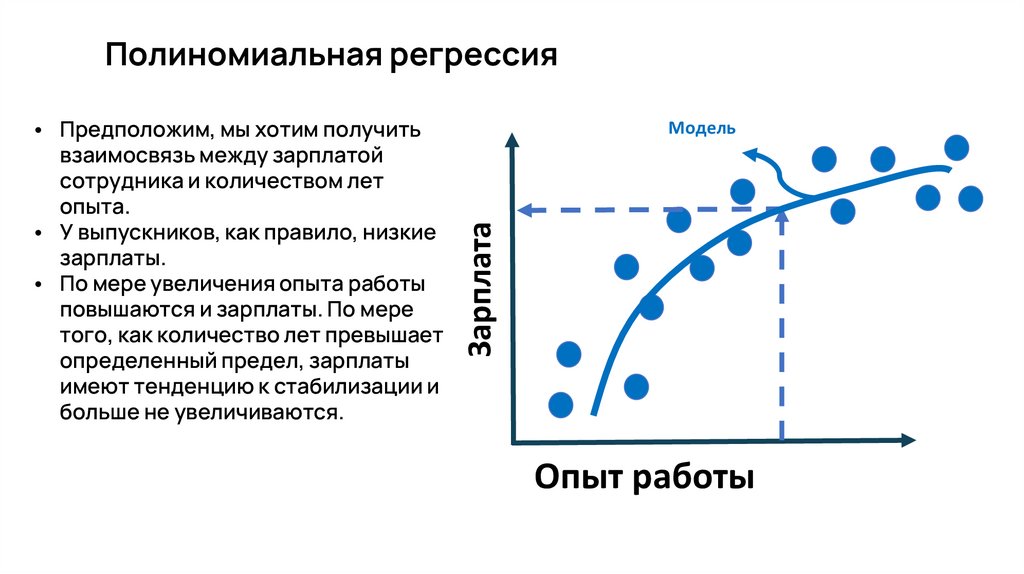
• Предположим, мы хотим получить
взаимосвязь между зарплатой
сотрудника и количеством лет
опыта.
• У выпускников, как правило, низкие
зарплаты.
• По мере увеличения опыта работы
повышаются и зарплаты. По мере
того, как количество лет превышает
определенный предел, зарплаты
имеют тенденцию к стабилизации и
больше не увеличиваются.
Опыт работы

4.

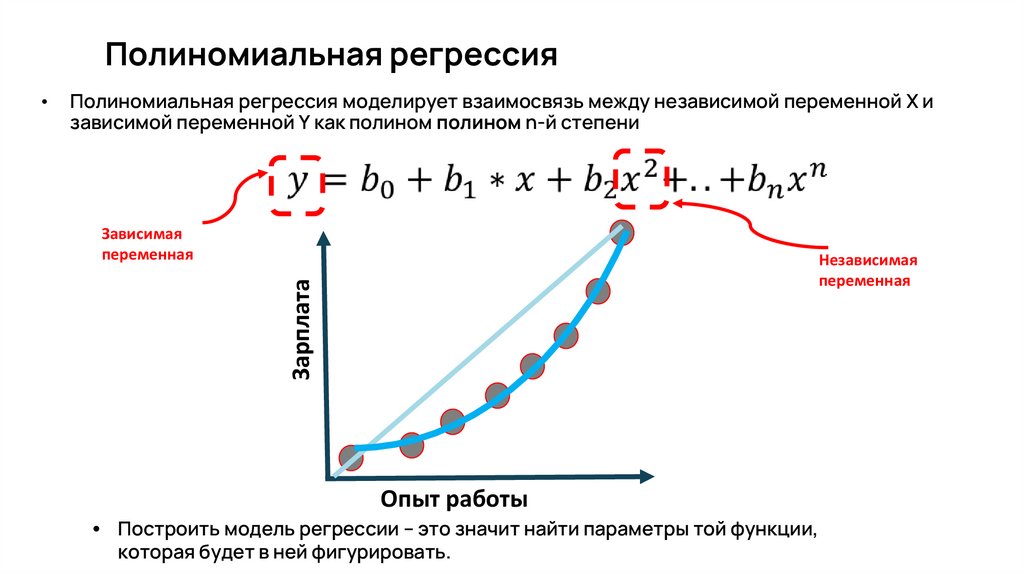
Полиномиальная регрессия
Полиномиальная регрессия моделирует взаимосвязь между независимой переменной X и
зависимой переменной Y как полином полином n-й степени
Зависимая
переменная
Независимая
переменная
Зарплата
Опыт работы
• Построить модель регрессии – это значит найти параметры той функции,
которая будет в ней фигурировать.

5.

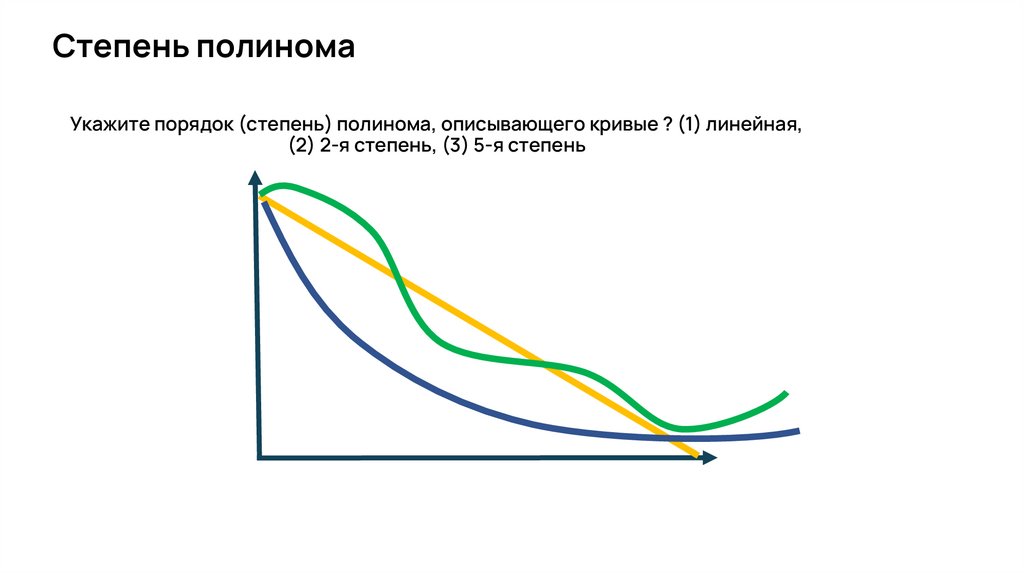
Степень полинома
Укажите порядок (степень) полинома, описывающего кривые ? (1) линейная,
(2) 2-я степень, (3) 5-я степень

6.

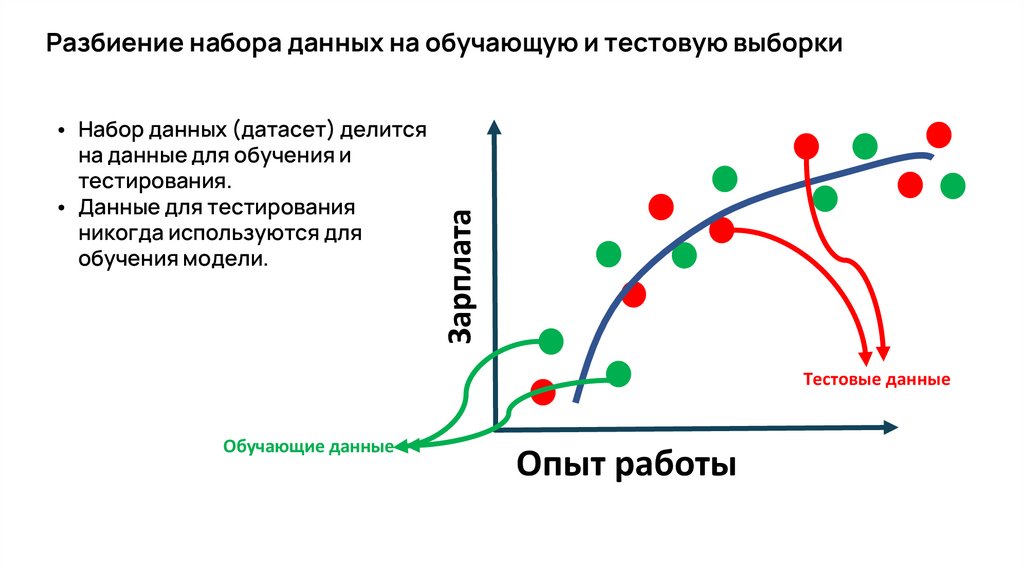
• Набор данных (датасет) делится
на данные для обучения и
тестирования.
• Данные для тестирования
никогда используются для
обучения модели.
Зарплата
Разбиение набора данных на обучающую и тестовую выборки
Тестовые данные
Обучающие данные
Опыт работы

7.

Высокий порядок полиномиальной модели переобученная модель
• Полиномиальная модель высокого
порядка очень гибкая и может идеально
соответствовать обучающему набору
данных.
• Но при этом иметь очень большую ошибку
на тестовых данных.

8.

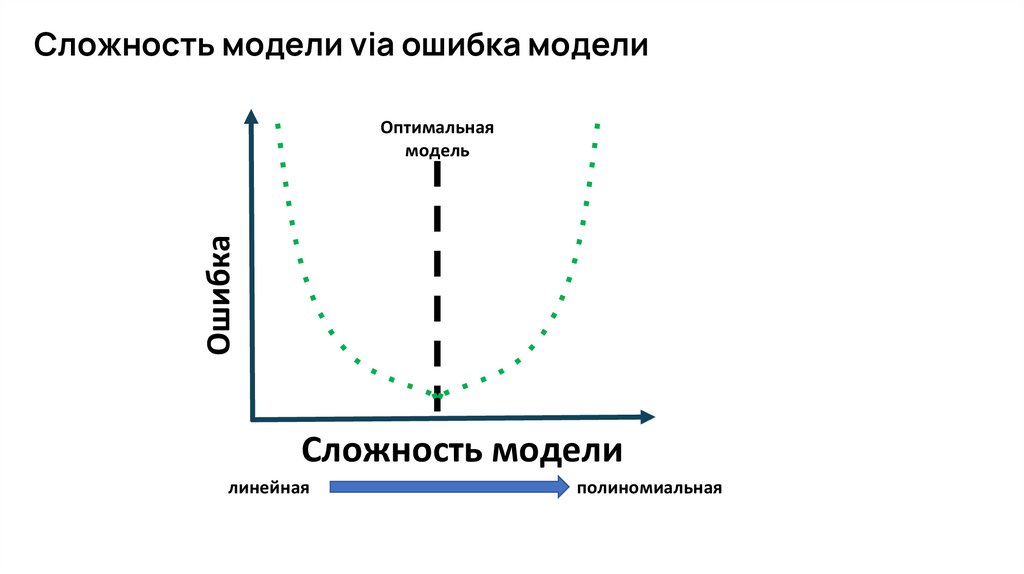
Сложность модели via ошибка модели
Ошибка
Оптимальная
модель
Сложность модели
линейная
полиномиальная

9.

Средняя абсолютная ошибка (MAE – mean absolute error)
• Средняя абсолютная ошибка (MAE) рассчитывается путем вычисления средней абсолютной
разницы между прогнозами модели и истинными (фактическими) значениями.
MAE - это линейная оценка, которая означает, что все индивидуальные различия взвешены
одинаково в среднем. Например, разница между 10 и 0 будет вдвое больше разницы между 5 и 0.
MAE рассчитывается следующим образом:
• Рассчитайте ошибку (остаток) в каждой точке данных.
• Вычислите абсолютное значение (чтобы избавиться от знака).
• Рассчитайте среднее значение всех остатков.
Если MAE равно нулю, это означает, что прогнозы модели идеальны (в реальной жизни не бывает).

10.

Средняя квадратическая ошибка (MSE – mean squared error)
• Среднеквадратичная ошибка (MSE) очень похожа на среднюю абсолютную ошибку (MAE), но
вместо использования абсолютных значений вычисляются квадраты разницы между прогнозами
модели и обучающим набором данных (истинные значения).
• Значения MSE обычно больше по сравнению с MAE, поскольку остатки возводятся в квадрат. В
случае выбросов данных MSE станет намного больше по сравнению с MAE. В MSE ошибка
увеличивается квадратично, в то время как ошибка увеличивается пропорционально в MAE.
• В MSE, поскольку ошибка возводится в квадрат, любая ошибка прогнозирования выявляется (+).
Ошибка никогда не бывает отрицательной.
• MSE рассчитывается следующим образом:
Недостатки:
Если выполнить очень плохой прогноз, возведение в квадрат сделает ошибку еще больше, и это
может исказить метрику в сторону переоценки отрицательных свойств модели.
Это особенно сказывается, если у нас есть зашумленные данные (данные, которые по какой-либо
причине не совсем надежны) - даже в «идеальной» модели может быть высокий MSE в этой ситуации,
поэтому становится трудно судить, насколько точна наша модель.
С другой стороны, если все ошибки малы или, скорее, меньше 1, то ощущается противоположный
эффект: мы можем недооценивать недостатки модели.

11.

Среднеквадратическая ошибка (RMSE - root mean square error)
Среднеквадратическая ошибка (RMSE) представляет собой стандартное отклонение остатков (то
есть: различия между прогнозами модели и истинными значениями (данные обучения)). RMSE
можно легко интерпретировать по сравнению с MSE, потому что единицы RMSE совпадают с
единицами вывода. RMSE дает оценку того, насколько сильно рассеиваются остатки. RMSE
рассчитывается следующим образом:
• Среднеквадратическая ошибка (RMSE)
RMSE - это просто квадратный корень из MSE. Квадратный корень введен, чтобы масштаб ошибок
был таким же, как масштаб целей.

12.

Средняя абсолютная ошибка в процентах (MAPE - mean absolute
percentage error)
• Значения MAE могут находиться в диапазоне от 0 до бесконечности, что затрудняет
интерпретацию результата по сравнению с данными обучения. Средняя абсолютная процентная
ошибка (MAPE) эквивалентна MAE, но предоставляет ошибку в процентной форме и,
следовательно, преодолевает ограничения MAE. MAPE может иметь некоторые ограничения, если
значение точки данных равно нулю (поскольку задействована операция деления) MAPE
рассчитывается следующим образом:

13.

R квадрат (