Общие сведения о функциях

1. Функция и её свойства.

2.

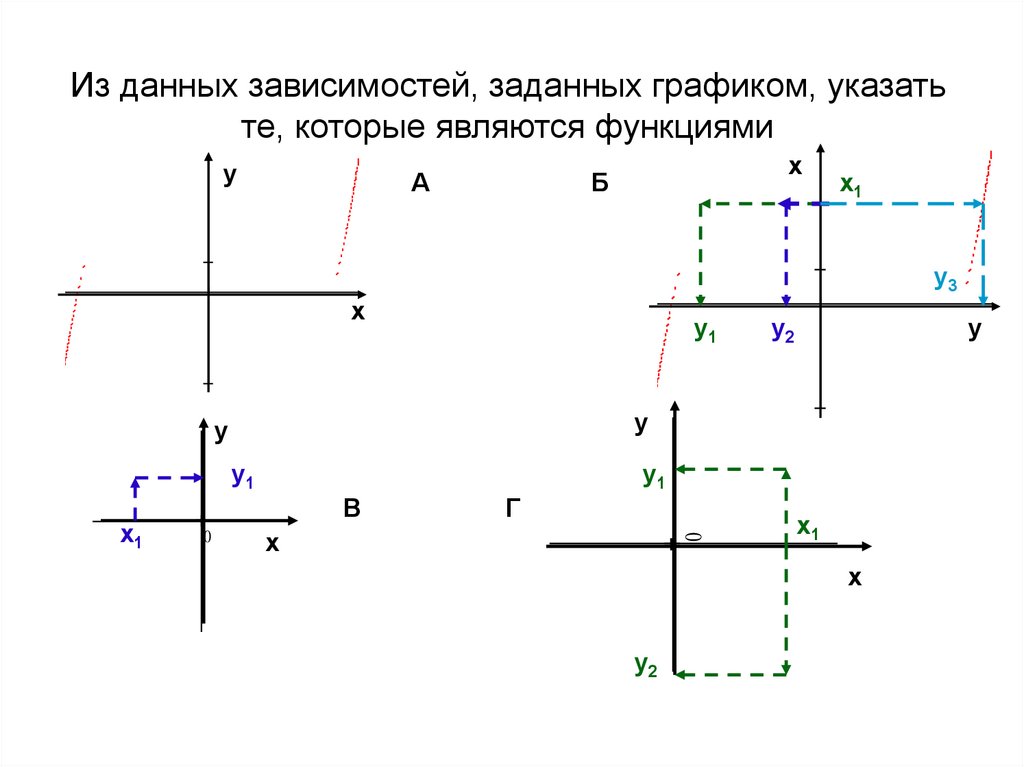
8
Из данных зависимостей, заданных графиком, указать
те, которые являются функциями
8
y
х
Б
A
f( x)
x1
f( x)
y3
х
y1
y2
y
x
5
3
y 3
y
y1
0
x
5
х1
10
x1
Г
0
5
3
y1
В
f( x)
x
x
7
5
3
5
5
5
10
x
7
5
y2
5
10
( x)
10
5
x

3.

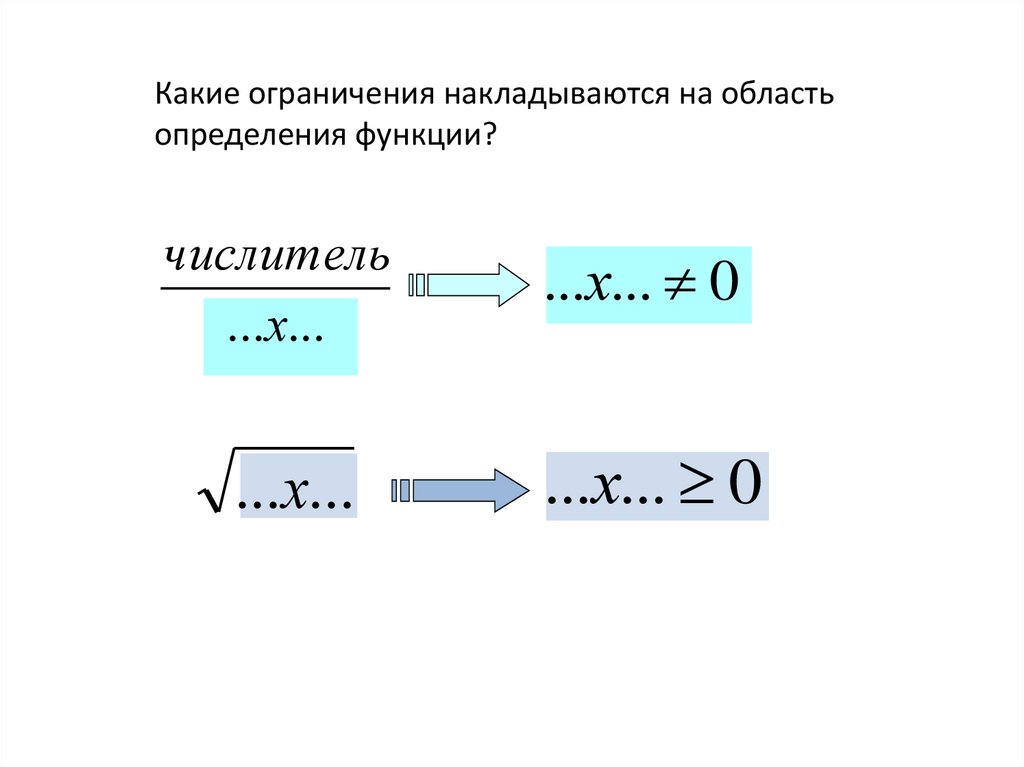
Какие ограничения накладываются на область
определения функции?
числитель
...х...
...х... 0
...х...
...х... 0

4.

Поставить в соответствие функцию, заданную
формулой и её область определения.
а)
y
x 4
1) D(y) = R, x ≠ 3
2x 5
б) y 2
x 9
2) D(y) = R
x2 9
в) y
x 3
3) D(y) = ( 4;
[ +∞)
3 x 11
г) y 2
x 7
4) D(y) = R, x ≠ ± 3

5.

Придумайте функцию по её области определения.
D(y) = R, x ≠ 5
x2 +3x – 2
числитель
y
( х 5
)(x2+26)
3 +3x2 – 12
xчислитель
D(y) = R, x ≠ ±5
y
D(y) = R, x ≥ 5
y
D(y) = R
x–2
÷èñëèòåëü
y
õ2 15
х 5 х 5
x 5 + 2x – 15

6.

Функция
чётная
нечётная
D(f) – симметрична относительно 0
f (– x) = f (x)
f (– x) = – f (x)
Что можно сказать про графики чётной и нечётной функций
График
Симметричен
относительно оси
ординат
Симметричен
относительно начала
координат

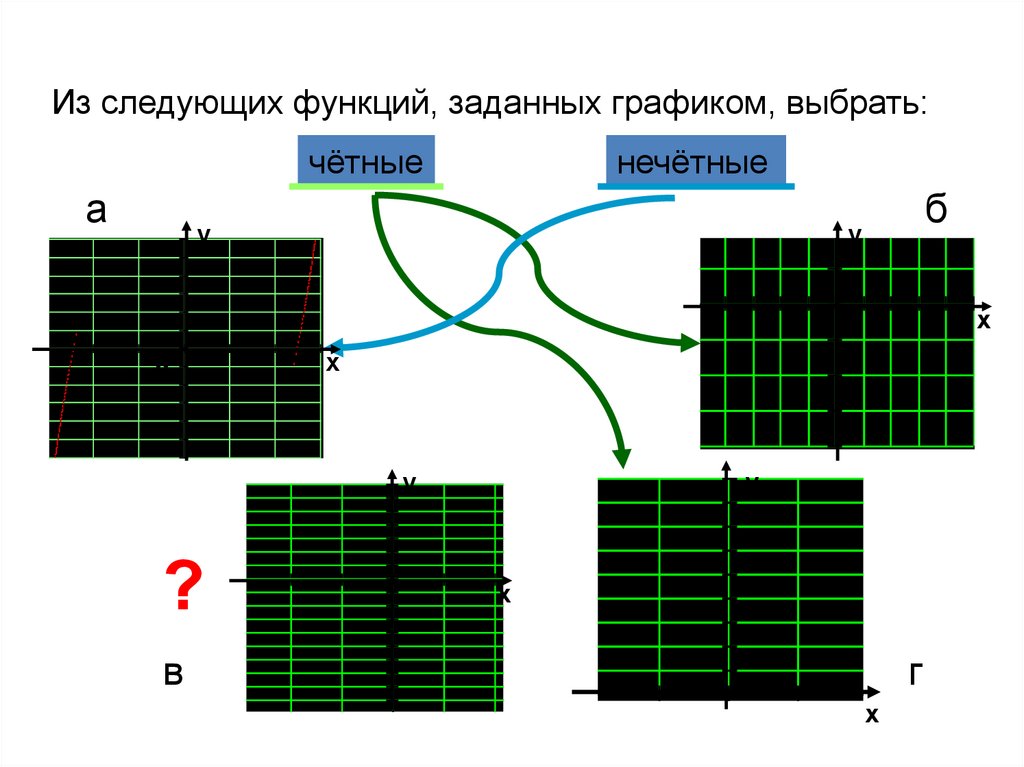
7.

Из следующих функций, заданных графиком, выбрать:
чётные
а
нечётные
у
6
10
f( x)
х
f( x)
х
0
б
у
20
6
3
x
3
7
?
х
f( x)
5
10
у
у
г
0
10
x
5
y
в
5
x
5
10
x
х
10

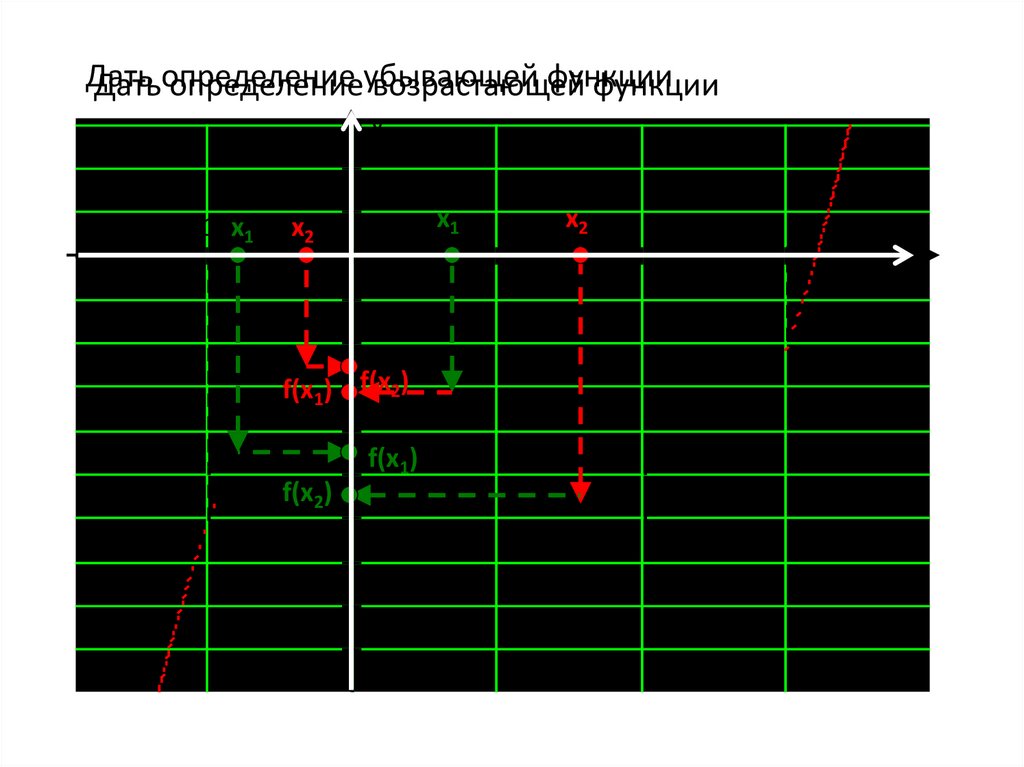
8.

Дать
функции
Датьопределение
определениеубывающей
возрастающей
функции
у
3
– 1 х1
х2
0
х1
х2
2
3
х
f(x1) f(х2)
f( x)
f(x1)
f(х2)
10
2
x
4

9.

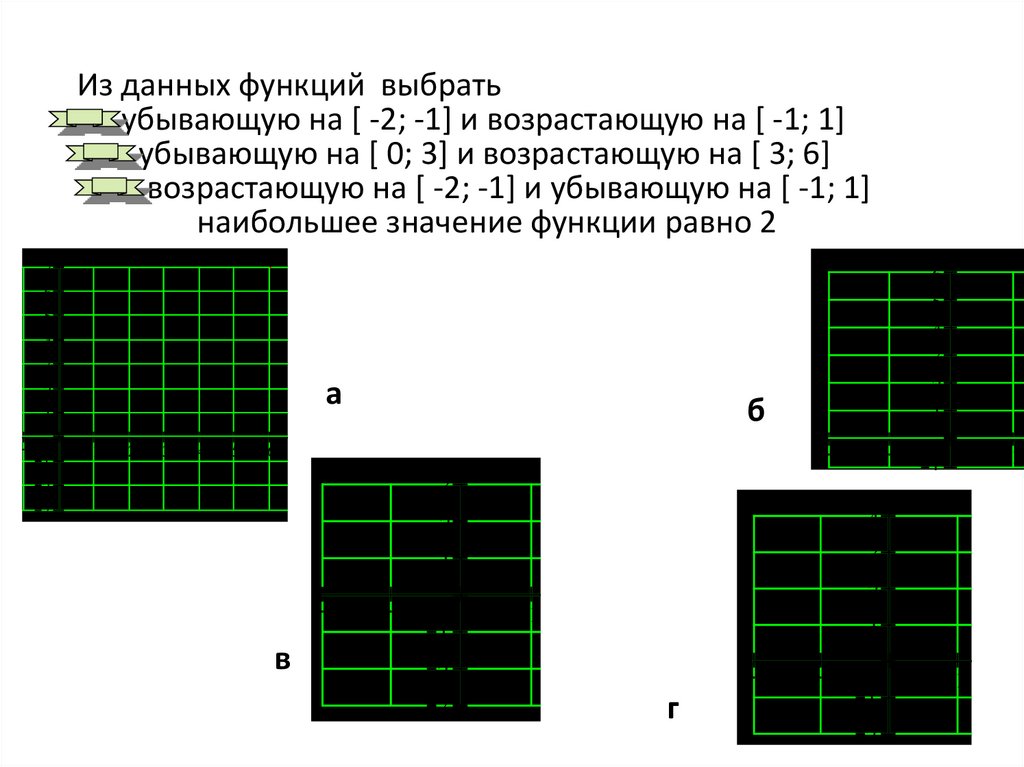
Из данных функций выбрать
убывающую на [ -2; -1] и возрастающую на [ -1; 1]
убывающую на [ 0; 3] и возрастающую на [ 3; 6]
возрастающую на [ -2; -1] и убывающую на [ -1; 1]
наибольшее значение функции равно 2
7
6
6
5
4
3
2
1
6
5
4
3
2
1
1
2
0
1
2
3
4
5
6
б
7
1
2
1
3
3
3
2
c( x)
а
2
1
2
x
7
2 4
4
1
0
1
x
3
1
2
f( x)
2
1
0
1
2
1
в
g( x)
2
3
2
г 2
3
2
1
x
2
1
0
1
2
1
2

10.

Самостоятельная
2 вариант
1 вариант
работа
1. Найти область определения функции
Проверим решение
2 x 13
x 2
y 2
x 5
y
x 2 0
2
x 5 0
x 2
x R
x 7 0
x 7 0
x 7 0
x 7 0
x 7 0
x 7
D( y ) [2; )
D ( y ) ( 7; )
x 7

11.

1 вариант
2. Исследовать на чётность функции
y x 5x
3
2 вариант
x 1
y
x 2
5
5
x 3 5x
– многочлен
3
5
3
5
2) y( x) ( x) 5( x) x 5x y( x)
функция нечётная
1) D(y) = R, т.к.
Функция не является ни чётной, ни
нечётной, т.е. функция общего вида
1) D(y) = R, x ≠ 2 – не симметрична относительно 0

12.

1 вариант
Построить
график
функции
3. 3.
Построить
график
функции
возрастающей на [– 4; 2]
и убывающей на [ 2; 6 ]
Е(у) = [ -4; 7]
2 вариант
убывающей на [– 6; 0]
и возрастающей на [ 0; 4 ]
E(y) = [ -4; 6]

13.

Исследуем функцию
y 4 x 2 по следующей схеме:
• Область определения функции
• Множество значений функции (составлением обратной
функции, если это возможно)
• Чётность или нечётность функции
• Точки пересечения функции с осями координат
• График функции
• Промежутки знакопостоянства функции
• Промежутки монотонности функции
• Ограниченность функции

14.

Найдём область определения функции
y 4 x
2
4 x2 0
2 x 2 x 0
2 x 0 ; 2 x 0
x 2 ; x 2
–
-2
D(y) = [ – 2; 2 ]
–
+
2
х

15.

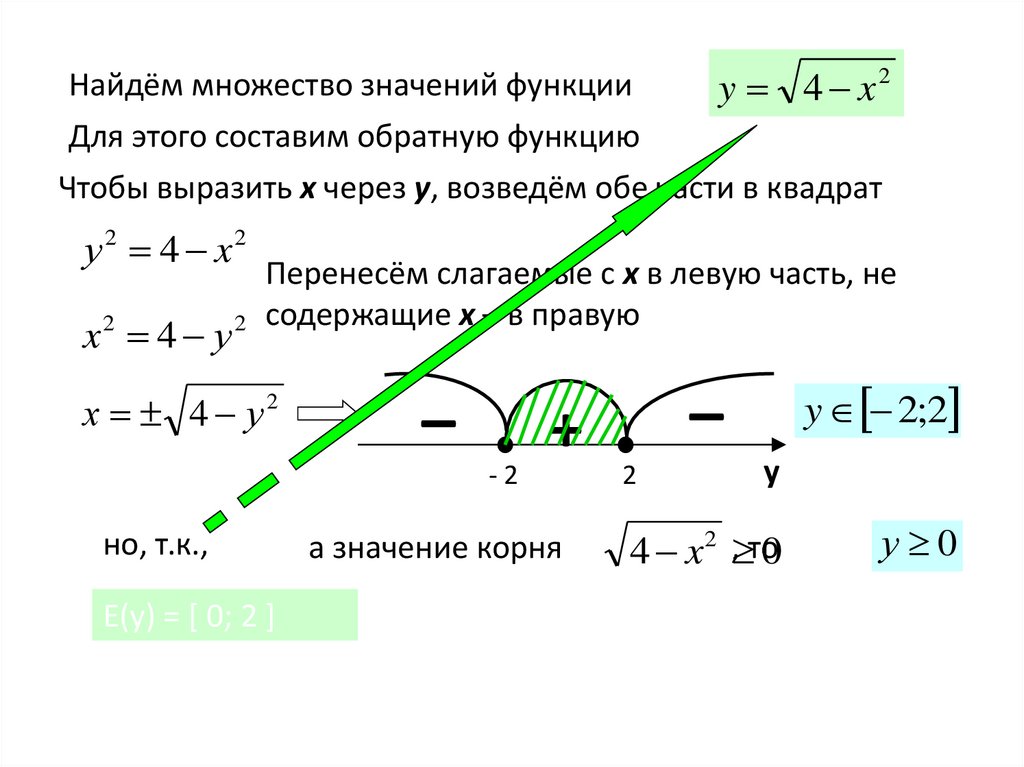
Найдём множество значений функции
y 4 x2
Для этого составим обратную функцию
Чтобы выразить х через у, возведём обе части в квадрат
у 2 4 x2
x2 4 у
Перенесём слагаемые с х в левую часть, не
2 содержащие х – в правую
х 4 у2
но, т.к.,
Е(у) = [ 0; 2 ]
–
+
-2
2
а значение корня
y 2;2
–
у
, то
4 x2
0
у 0

16.

Исследуем на чётность функцию
1)
-2
2)
y 4 x2
D(y) = [ – 2; 2 ]
0
2 х
симметрична относительно нуля
y ( х) 4 ( x) 2 4 х 2 у ( х)
функция чётная

17.

Найдём точки пересечения функции
с осями координат
y 4 x2
Точки пересечения
с осью ОУ: х = 0;
y 4 02 4 2 (0; 2)
с осью ОХ: у = 0;
0 4 x2
4 x2 0
решаем уравнение
x 2 4 x 2
( – 2; 0), ( 2; 0)