Степенные функции, их свойства и графики

1.

Степенные функции,
их свойства и
графики

2.

Степенными функциями
называются функции вида
у = хr, где r – заданное
рациональное число

3.

y
у = х2
у = х4
у = х6
-1 0 1 2
x
Показатель r = 2n – чётное натуральное число

4.

Показатель r = 2n – чётное натуральное число
у = х2, у = х4 , у = х6, у = х8, …
у
D( y ) : x R
у = х2n
Е ( y) : у 0
0
График чётной функции
симметричен относительно
оси Оу.
х
Функция у=х2n чётная,
т.к. (–х)2n = х2n
Функция убывает на
промежутке
( ;0]
Функция возрастает
на промежутке
[0; )

5.

Показатель r = 2n-1
нечётное
натуральное число
y
у = х3
у = х5
у = х7
-1 0 1 2
x

6.

Показатель r = 2n-1 – нечётное натуральное число
у = х3, у = х5, у = х7, у = х9, …
у
D( y ) : x R
Е ( y) : у R
у = х2n-1
Функция у=х2n-1 нечётная,
т.к. (–х)2n-1 = – х2n-1
0
х
Функция возрастает
на промежутке ;
График нечётной
функции симметричен
относительно начала
координат – точки О.

7.

Показатель r - целое
отрицательное нечётное
число
y
у = х-1
у = х-3
у = х-5
-1 0 1 2
x

8.

Показатель r = – (2n-1), где n – натуральное число
у = х-3, у = х-5 , у = х-7, у = х-9, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
( 2 n 1)
Функция у=х-(2n-1)
нечётная,
–(2n-1) = –х–(2n-1)
т.к.
(–х)
х
1
y
1
х
2 n 1
Функция убывает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )

9.

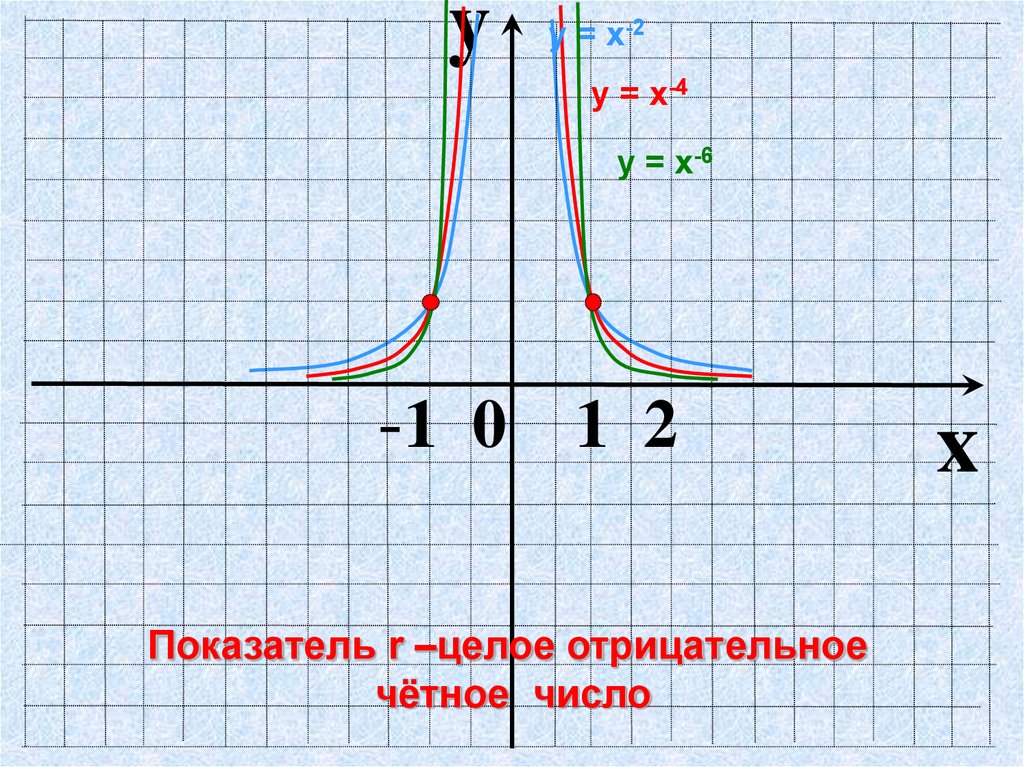
y
у = х-2
у = х-4
у = х-6
-1 0 1 2
Показатель r –целое отрицательное
чётное число
x

10.

Показатель r = – 2n, где n – натуральное число
у = х-2, у = х-4 , у = х-6, у = х-8, …
у
D( y ) : x 0
Е ( y) : у 0
0
y х
2 n
1
1
y 2n
х
х
Функция у=х2n чётная,
т.к. (–х)-2n = х-2n
Функция возрастает на
промежутке
( ;0)
Функция убывает
на промежутке
(0; )

11.

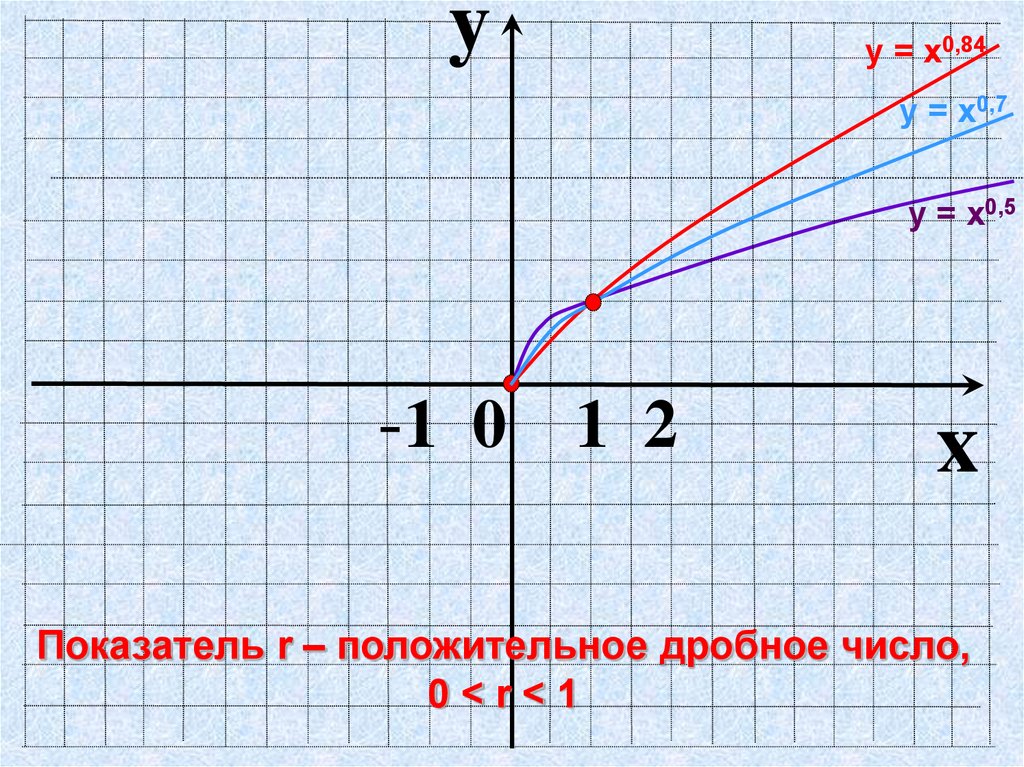
y
у = х0,84
у = х0,7
у = х0,5
-1 0 1 2
x
Показатель r – положительное дробное число,
0<r<1

12.

Показатель r – положительное дробное число, 0 < 1r < 1
у
у = х0,3,
у = х0,7, у = х0,12,
у х3 …
D( y ) : x 0
у х
r
Е ( y) : у 0
Функция возрастает на
0
1
х промежутке
[0; )

13.

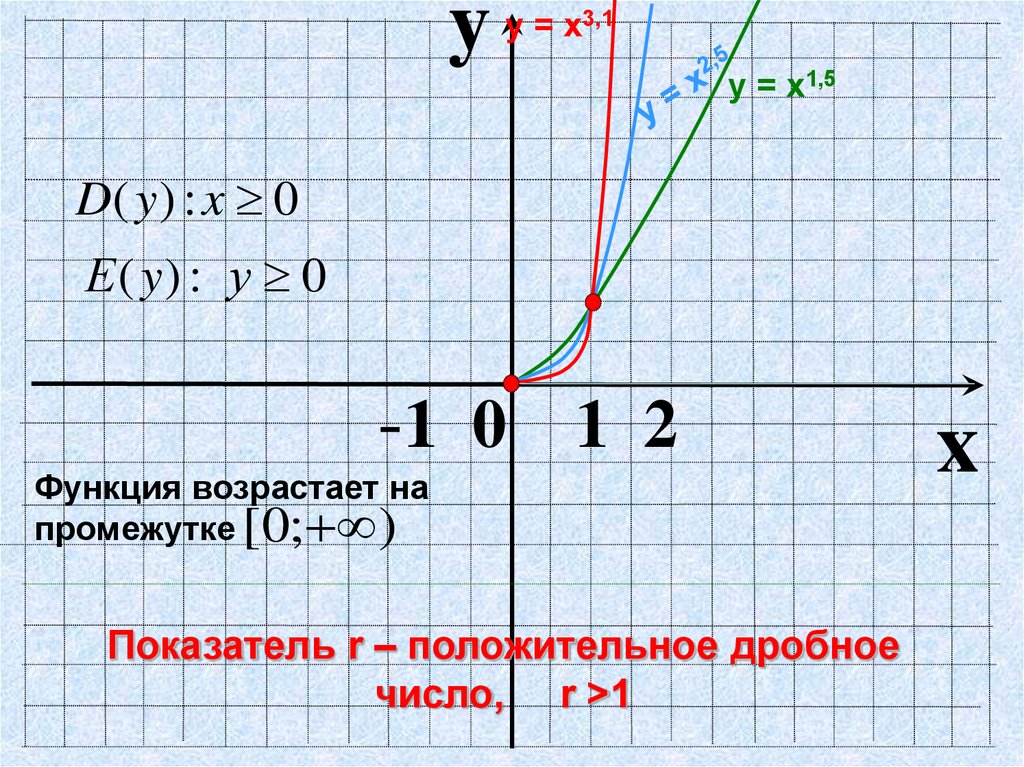
y
у = х3,1
у = х1,5
D( y ) : x 0
Е ( y) : у 0
-1 0 1 2
Функция возрастает на
промежутке [0; )
Показатель r – положительное дробное
число, r >1
x

14.

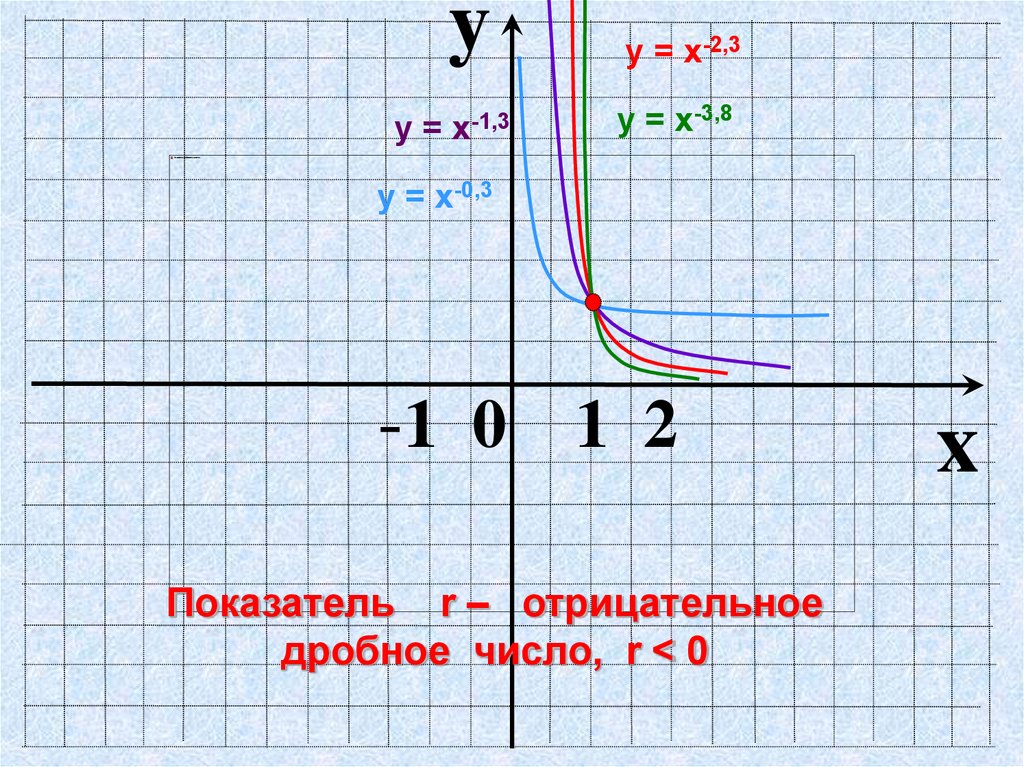
y
у = х-1,3
у = х-2,3
у = х-3,8
у = х-0,3
-1 0 1 2
Показатель r – отрицательное
дробное число, r < 0
x

15.

Показатель r – отрицательное дробное число 1
у
у=
х-1,3,
у=
х-0,7,
у=
х-2,12,
у х
3
…
D( y ) : x 0
Е ( y) : у 0
Функция убывает на
0
1
х промежутке
(0; )

16.

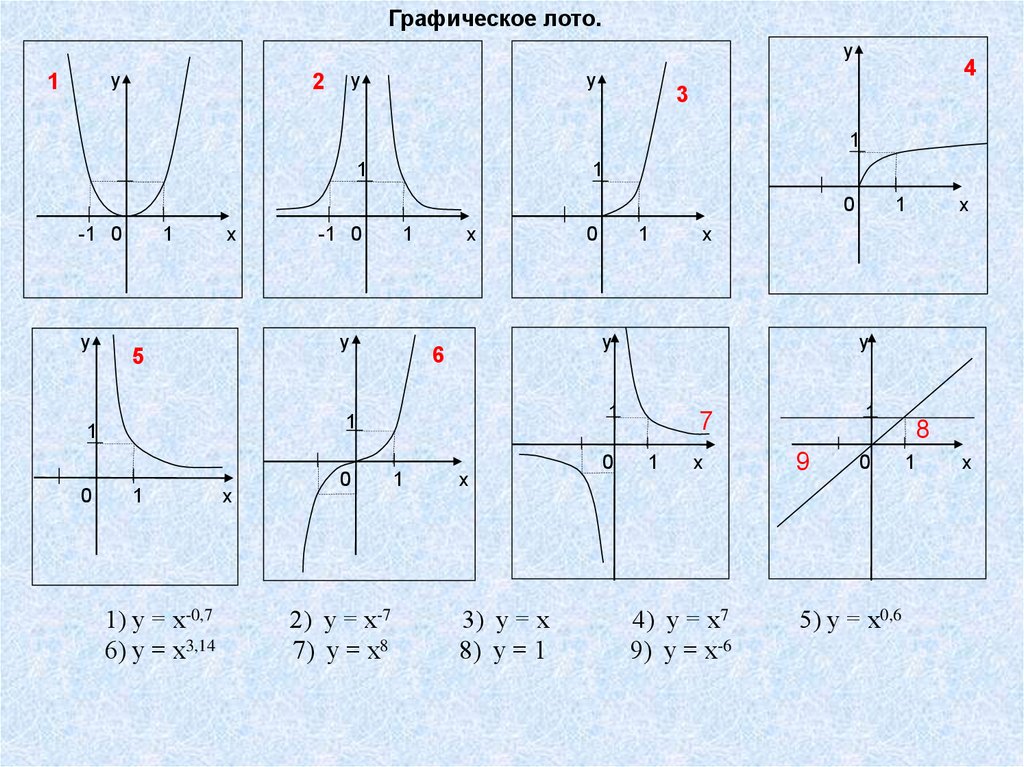
Графическое лото.
у
у
1
у
2
у
4
3
1
1
1
0
-1 0
у
1
х
х
1
у
5
1
1) у = х-0,7
6) у = х3,14
х
0
2) у = х-7
7) у = х8
0
1
у
1
1
х
у
6
1
1
0
-1 0
х
3) у = х
8) у = 1
0
х
1
1
7
1
х
4) у = х7
9) у = х-6
9
0
5) у = х0,6
8
1
х

17.

у
у
у х
0
у х
1
4
3
1
3
х
0
1
х
Пользуясь рисунком, найти промежутки, на которых
график функции у х
лежит выше (ниже) графика
функции у = х.

18.

у
у
у х
0
у х
1
4
3
1
3
х
0
1
х
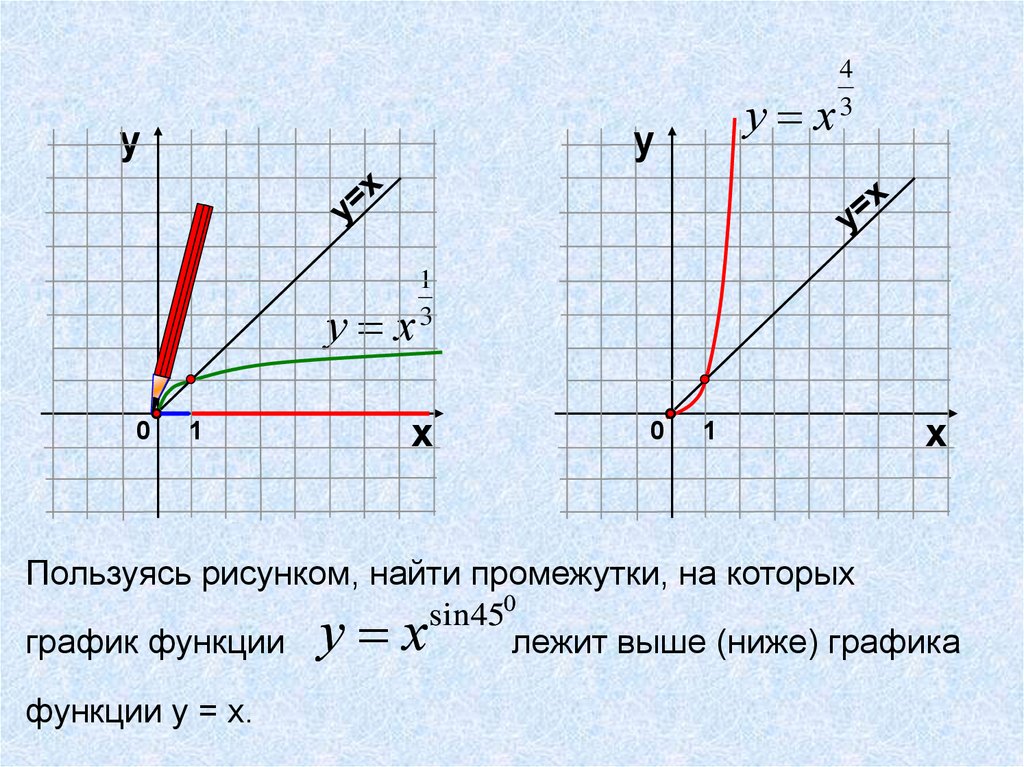
Пользуясь рисунком, найти промежутки, на которых
график функции
функции у = х.
у х
sin 450
лежит выше (ниже) графика

19.

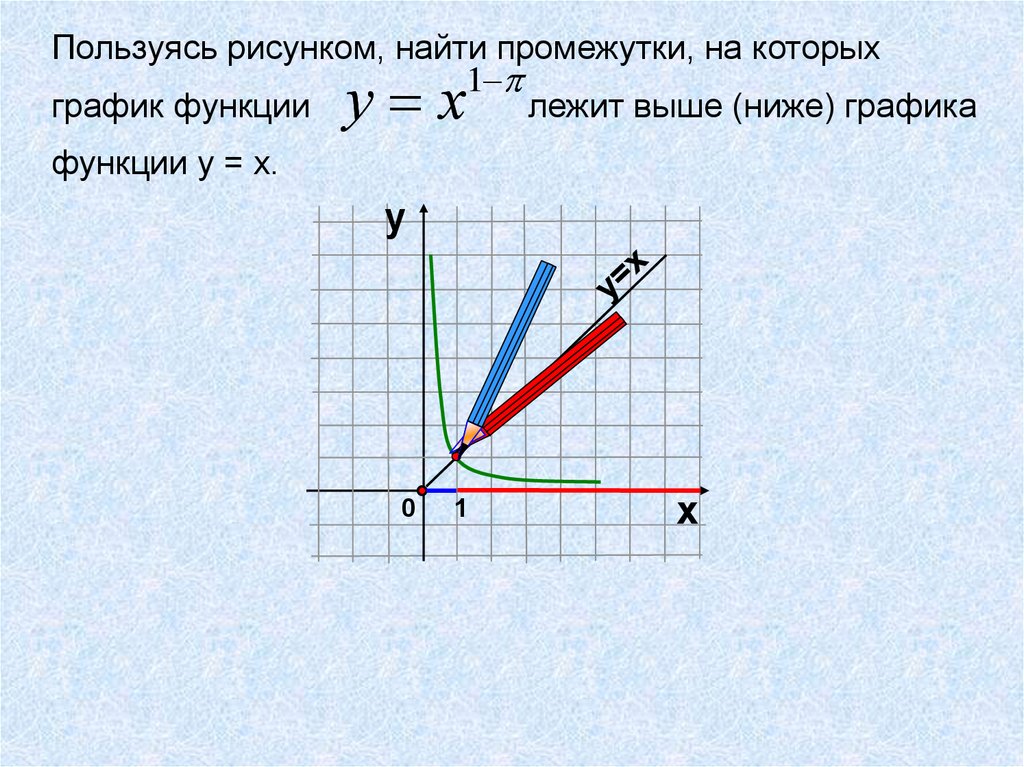
Пользуясь рисунком, найти промежутки, на которых
1
график функции
лежит выше (ниже) графика
у х
функции у = х.
у
0
1
х

20.

Преобразования
графиков
степенных функций

21.

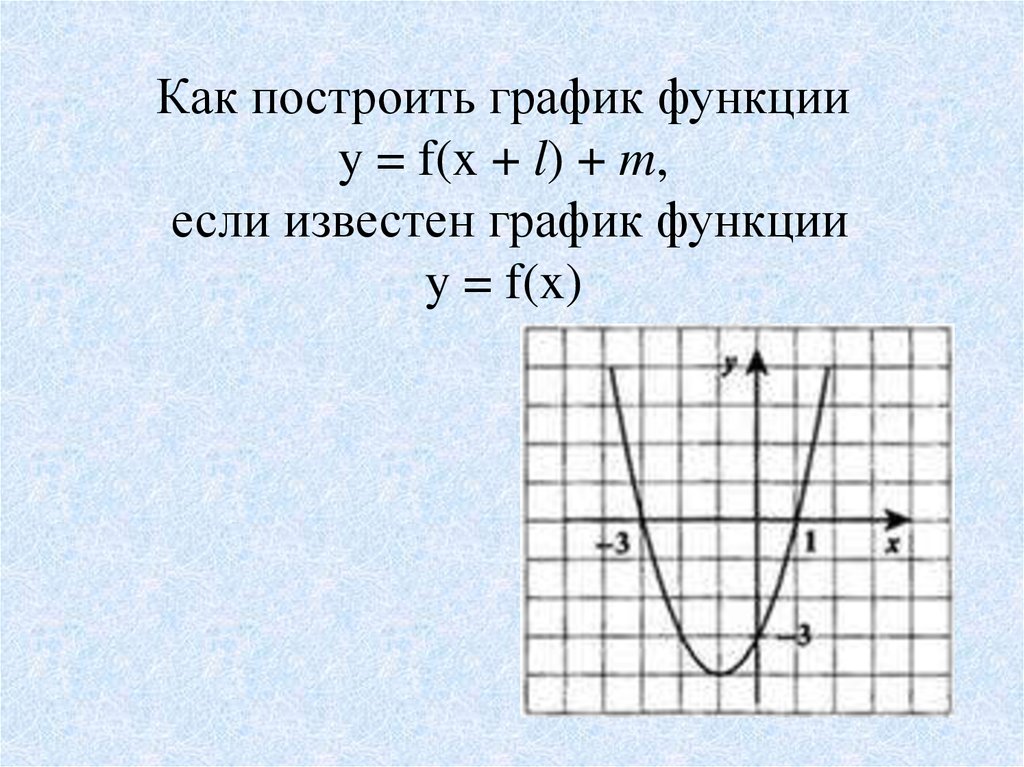
Как построить график функции
y = f(x + l),
если известен график функции
y = f(x)

22.

y
у = х-4
-1 0 1 2
у = (х – 2)-4
x

23.

Как построить график функции
y = f(x) + m,
если известен график функции
y = f(x)

24.

y
у = х-4
-1 0 1 2
у = х– 4 – 3
x

25.

Как построить график функции
y = f(x + l) + m,
если известен график функции
y = f(x)

26.

y
у = х-4
у = (х+1)– 4 – 3
-1 0 1 2
x

27.

y
у = (х-2)– 3– 1
у = х-3
-1 0 1 2
x

28.

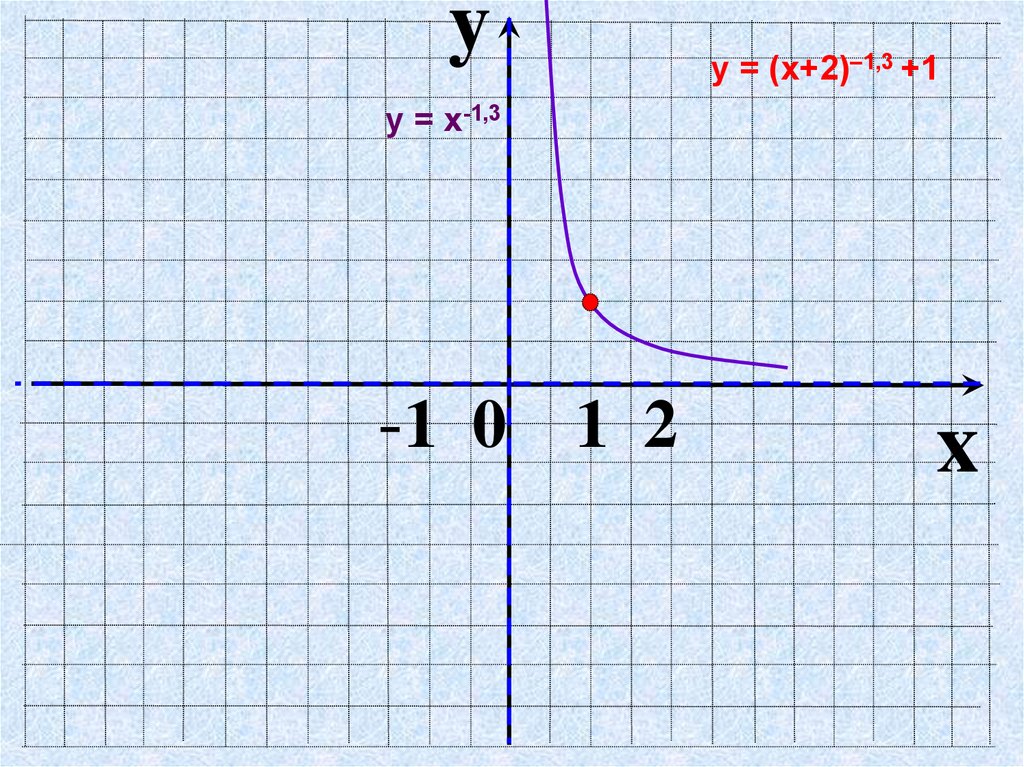
y
у = (х+2)–1,3 +1
у = х-1,3
-1 0 1 2
x

29.

Найдём производную функции:
Пример 1.
1
1
2 3
а ) у 3х ; у 3 х 3 х 2х 3 ;
3
4
4
11
11
4
б ) у 7х 7 ; у 7 х 7 7 х 7 4х 7 ;
7
5
3
5
5
в ) у 8(6х 5)8 ; у 8 6х 5 8 8 6 96х 5) 8
8
2
3
2
3
3
8
30(6х 5) .
При этом было использовано правило дифференцирования
( f (ax b )) af (ax b ).

30.

Исследуем функцию
Пример 2.
3
1
2
y x 2 2x 2
3
На монотонность и экстремумы и
построим её график.
1. Найдём производную функции:
1
1
1
2
2 3 12
1 2
x 1
2
2
y x 2x x 2 x x x 1
2
3
3 2
x2
3
2
1
2
2. Функция существует при х ≥ 0, производная существует при х>0.
Поэтому критических точек у функции нет. Стационарную точку
x 1
0 , откуда х=1.
найдём из условия y 0 или
1
x2
3. Очевидно, что при х (0;1], значение у'≤0 и функция у(х) убывает
на этом промежутке. При х [1;+∞) значение у'≥0 и функция у(х)
возрастает. В точке х = 1 функция у(х) имеет минимум
э
э
у min
2
4
2
3
3

31.

Исследуем функцию
Пример 2.
3
1
2
y x 2 2x 2
3
На монотонность и экстремумы и
построим её график.
1. Найдём производную функции:
1
1
1
2
2 3 12
1 2
x 1
2
2
y x 2x x 2 x x x 1
2
3
3 2
x2
3
2
1
2
2. Функция существует при х ≥ 0, производная существует при х>0.
Поэтому критических точек у функции нет. Стационарную точку
x 1
0 , откуда х=1.
найдём из условия y 0 или
1
x2
3. Очевидно, что при х (0;1], значение у'≤0 и функция у(х) убывает
на этом промежутке. При х [1;+∞) значение у'≥0 и функция у(х)
возрастает. В точке х = 1 функция у(х) имеет минимум
э
э
у min
2
4
2
3
3